Hace un año y medio, publiqué el artículo
"Matemáticas en los dedos: métodos de mínimos cuadrados" , que recibió una respuesta muy decente, que, entre otras cosas, consistió en el hecho de que propuse dibujar un búho. Bueno, como un búho, debes explicarlo de nuevo. En una semana, sobre este tema exactamente, comenzaré a dar varias conferencias a estudiantes de geología; Aprovecho esta oportunidad, presento aquí los puntos principales (adaptados) como un borrador. ¡Mi objetivo principal no es dar una receta preparada de un libro sobre comida sabrosa y saludable, sino explicar por qué es así y qué más hay en la sección correspondiente, porque las conexiones entre las diferentes secciones de matemáticas son las más interesantes!
Por el momento, tengo la intención de romper el texto de la siguiente manera:
Iré a los mínimos cuadrados un poco de lado, a través del principio de máxima verosimilitud, y requiere una orientación mínima en la teoría de la probabilidad. Este texto está diseñado para el tercer año de nuestra facultad de geología, lo que significa (¡desde el punto de vista del equipo involucrado!) Que un estudiante de secundaria interesado con el celo apropiado debería poder entenderlo.
¿Cuán sólido es el teórico o crees en la teoría de la evolución?
Un día me preguntaron si creo en la teoría de la evolución. Pausa en este momento, piensa en cómo responderás.

Personalmente, me sorprendió, respondió que me parece creíble y que la cuestión de la fe no surge aquí en absoluto. La teoría científica tiene poco que ver con la fe. En resumen, la teoría solo construye un modelo del mundo que nos rodea, no hay necesidad de creer en él. Además,
el criterio de Popper requiere una teoría científica para poder refutar. Y también una teoría sólida debe poseer, en primer lugar, poder predictivo. Por ejemplo, si modifica genéticamente los cultivos de tal manera que ellos mismos produzcan pesticidas, es lógico que aparezcan insectos resistentes a ellos. Sin embargo, es significativamente menos obvio que este proceso puede ralentizarse si se cultivan plantas comunes junto con otras genéticamente modificadas. Basado en la teoría de la evolución, la simulación correspondiente hizo
tal predicción , y parece
confirmarse .
¿Y qué tienen que ver los mínimos cuadrados con él?
Como mencioné anteriormente, iré a los mínimos cuadrados a través del principio de máxima verosimilitud. Vamos a ilustrar con un ejemplo. Supongamos que estamos interesados en datos sobre el crecimiento de pingüinos, pero solo podemos medir algunas de estas hermosas aves. Es bastante lógico introducir un modelo de distribución de crecimiento en la tarea; la mayoría de las veces es normal. La distribución normal se caracteriza por dos parámetros: valor medio y desviación estándar. Para cada valor fijo de los parámetros, podemos calcular la probabilidad de que se generen exactamente las mediciones que realizamos. Además, al variar los parámetros, encontramos aquellos que maximizan la probabilidad.
Por lo tanto, para trabajar con la máxima probabilidad, necesitamos operar en términos de teoría de la probabilidad. Un poco más abajo, en los dedos, definimos el concepto de probabilidad y probabilidad, pero primero me gustaría centrarme en otro aspecto. Sorprendentemente, rara vez veo personas pensando en la palabra "teoría" en la frase "teoría de la probabilidad".
¿Qué es aprender theorver?
Con respecto a los orígenes, los significados y el alcance de las estimaciones de probabilidad, el debate violento ha estado ocurriendo durante más de cien años. Por ejemplo,
Bruno De Finetti afirmó que la probabilidad no es más que un análisis subjetivo de la probabilidad de que algo suceda, y que esta probabilidad no existe fuera de la mente. Esta es la voluntad de una persona de apostar a que algo suceda. Esta opinión es directamente opuesta a la opinión de los
clásicos / freventistas sobre la probabilidad de un resultado específico de un evento, en el que se supone que el mismo evento puede repetirse varias veces, y la "probabilidad" de un resultado particular está relacionada con la frecuencia de un resultado específico que se cae durante las pruebas repetidas. Además de subjetivistas y freventistas, también hay objetivistas que sostienen que las probabilidades son aspectos reales del universo, y no solo descripciones del grado de confianza del observador.
Sea como fuere, pero las tres escuelas científicas en la práctica usan el mismo aparato basado en los axiomas de Kolmogorov. Demos un argumento indirecto, desde un punto de vista subjetivista, a favor de la teoría de la probabilidad, construida sobre los axiomas de Kolmogorov. Les damos a los axiomas un poco más tarde, pero para empezar asumiremos que tenemos una casa de apuestas que aceptará apuestas en la próxima Copa del Mundo. Tengamos dos eventos: a = el equipo de Uruguay se convertirá en el campeón, b = el equipo alemán se convertirá en el campeón. La casa de apuestas estima las posibilidades de que el equipo de Uruguay gane en un 40%, las posibilidades del equipo alemán en un 30%. Obviamente, tanto Alemania como Uruguay no pueden ganar al mismo tiempo, por lo tanto, la probabilidad de a∧b es cero. Bueno, al mismo tiempo, la casa de apuestas cree que la probabilidad de que Uruguay o Alemania (y no Argentina o Australia) gane es del 80%. Escribámoslo de la siguiente forma:

Si el corredor de apuestas afirma que su grado de confianza en el evento
a es 0.4, es decir,
P (a) = 0.4, entonces el jugador puede elegir si apostará a favor o en contra de decir
a , cantidades de apuestas que son compatibles con el grado de confianza del corredor de apuestas. Esto significa que el jugador puede apostar que el evento sucederá apostando cuatro rublos contra seis rublos de la casa de apuestas. O un jugador puede apostar seis rublos en lugar de cuatro rublos de una casa de apuestas que el evento no sucederá.
Si el grado de confianza del corredor de apuestas no refleja con precisión el estado del mundo, entonces podemos contar con el hecho de que a la larga perderá dinero para los jugadores cuyas creencias son más precisas. Además, en este ejemplo en particular, el jugador tiene una estrategia en la cual el corredor de apuestas
siempre pierde dinero. Vamos a ilustrarlo:

El jugador hace tres apuestas, y sea cual sea el resultado del campeonato, siempre gana. Tenga en cuenta que la consideración de las ganancias en principio no incluye si Uruguay o Alemania son los favoritos del campeonato, ¡la pérdida de la casa de apuestas está garantizada! Esta situación fue conducida por el hecho de que el corredor de apuestas no se guió por los fundamentos de la teoría de la probabilidad, habiendo violado el tercer axioma de Kolmogorov, traigamos los tres:
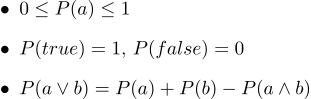
En forma de texto, se ven así:
- 1. Todas las probabilidades van de 0 a 1
- 2. Por supuesto, las declaraciones verdaderas tienen una probabilidad de 1, y ciertamente una probabilidad falsa de 0.
- 3. El tercer axioma es el axioma de la disyunción, es fácil de entender intuitivamente, observando que aquellos casos en los que el enunciado a es verdadero, junto con los casos en que b es verdadero, ciertamente cubre todos los casos en los que el enunciado a∨b es verdadero; pero en la suma de dos conjuntos de casos, su intersección ocurre dos veces, por lo tanto, es necesario restar P (a∧b).
En 1931, de Finetti
demostró una declaración muy fuerte:
Si el corredor de apuestas se guía por muchos grados de confianza, lo que viola los axiomas de la teoría de la probabilidad, entonces existe una combinación de apuestas de jugador que garantiza la pérdida del corredor de apuestas (el jugador gana) en cada apuesta.
Se puede considerar que los axiomas de las probabilidades limitan el conjunto de creencias probabilísticas que un agente puede tener. Tenga en cuenta que seguir al corredor de apuestas no implica los axiomas de Kolmogorov de que ganará (dejaremos de lado los problemas de comisión), pero si no los sigue, se garantizará que perderá. Tenga en cuenta que se han presentado otros argumentos a favor de la aplicación de probabilidades; pero fue el éxito
práctico de los sistemas de razonamiento basados en la teoría de la probabilidad lo que resultó ser un incentivo atractivo que provocó una revisión de muchos puntos de vista.
Entonces, abrimos ligeramente el velo de
por qué Theorver puede tener sentido, pero ¿qué tipo de objetos manipula? Toda la teoría se basa en solo tres axiomas; los tres involucran alguna función mágica
P. Además, al observar estos axiomas, me recuerda mucho la función del área de forma. Intentemos ver si el área funciona para determinar la probabilidad.
Definimos la palabra "evento" como "un subconjunto de un cuadrado de la unidad". Definimos la palabra "probabilidad de un evento" como "el área del subconjunto correspondiente". Hablando en términos generales, tenemos un gran objetivo de cartón, y nosotros, habiendo cerrado los ojos, le disparamos. Las posibilidades de que una bala caiga en un conjunto dado son directamente proporcionales al área del conjunto. Un evento confiable en este caso es el cuadrado completo, y obviamente falso, por ejemplo, cualquier punto del cuadrado. De nuestra definición de probabilidad se deduce que es imposible llegar al punto perfectamente (nuestra viñeta es un punto material). Realmente me gustan las imágenes, y dibujo muchas de ellas, ¡y el final no es una excepción! Vamos a ilustrar los tres axiomas:
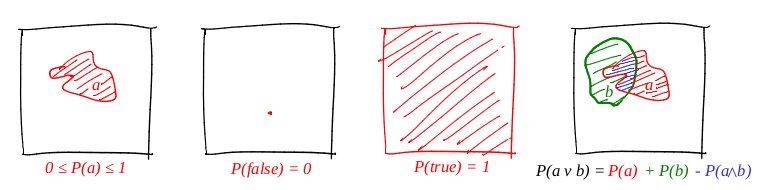
Entonces, se cumple el primer axioma: el área no es negativa y no puede exceder las unidades. Un evento confiable es todo el cuadrado, y uno deliberadamente falso es cualquier conjunto de área cero. ¡Y funciona perfectamente con la disyunción!
Máxima credibilidad con ejemplos
Ejemplo uno: lanzamiento de moneda
Veamos el ejemplo más simple de un lanzamiento de moneda, también conocido como
el esquema de Bernoulli . Se llevan a cabo
N experimentos, en cada uno de los cuales puede ocurrir uno de los dos eventos ("éxito" o "fracaso"), uno con probabilidad
p y el segundo con probabilidad
1-p . Nuestra tarea es encontrar la probabilidad de obtener exactamente
k éxitos en estos
n experimentos. Esta probabilidad nos da la fórmula de Bernoulli:
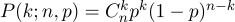
Tome una moneda común (
p = 0.5 ), tírela diez veces (
n = 10 ) y considere cuántas veces se caen las colas:
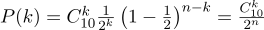
Aquí hay un gráfico de densidad de probabilidad:
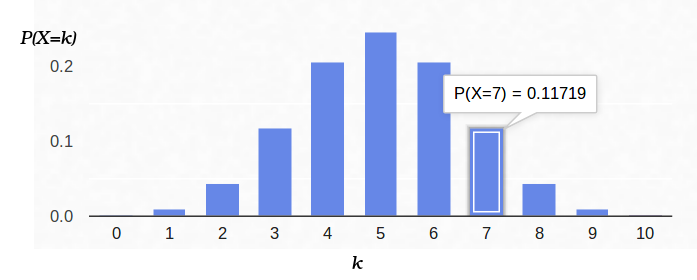
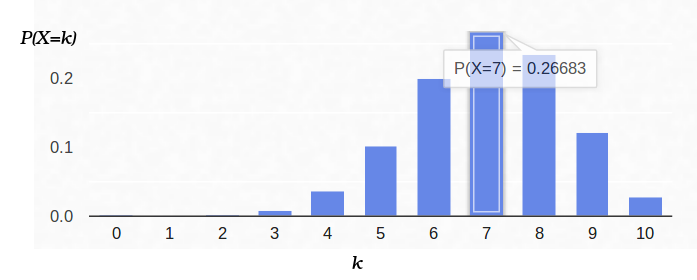
Por lo tanto, si fijamos la probabilidad del inicio del "éxito" (0.5), y también registramos el número de experimentos (10), entonces el número posible de "éxitos" puede ser cualquier número entero entre 0 y 10, sin embargo, estos resultados no son igualmente probables. Es obvio que obtener cinco "éxitos" es mucho más probable que ninguno. Por ejemplo, la probabilidad de contar siete colas es aproximadamente del 12%.
Ahora veamos la misma tarea desde el otro lado. Tenemos una moneda real, pero no sabemos su distribución de la probabilidad a priori de "éxito" / "fracaso". Sin embargo, podemos lanzarlo diez veces y contar el número de "éxitos". Por ejemplo, tenemos siete colas. ¿Cómo nos ayuda esto a evaluar
p ?
Podemos intentar arreglar
n = 10 y
k = 7 en la fórmula de Bernoulli, dejando
p un parámetro libre:

Entonces la fórmula de Bernoulli se puede interpretar como la
probabilidad del parámetro estimado (en este caso,
p ). Incluso cambié la letra de la función, ahora es
L (del inglés). Es decir, la probabilidad es la probabilidad de generar datos de observación (7 colas de 10 experimentos) para un valor dado de los parámetros.
Por ejemplo, la probabilidad de una moneda equilibrada (
p = 0.5), siempre que ocurran siete colas de diez tiros, es aproximadamente del 12%. Puedes trazar la función
L :
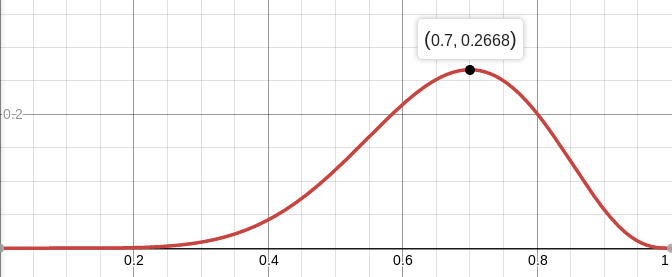
Entonces, estamos buscando un valor de parámetros que maximice la probabilidad de obtener las observaciones que tenemos. En este caso particular, tenemos una función de una variable, estamos buscando su máximo. Para facilitar la búsqueda, buscaré un máximo de no
L , sino
log L. El logaritmo es una función estrictamente monotónica, por lo que maximizar uno y el otro es exactamente lo mismo. Y el logaritmo divide el producto en una cantidad que es mucho más conveniente para diferenciar. Entonces, estamos buscando el máximo de esta función:

Para hacer esto, equiparamos su derivada a cero:
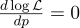
La derivada de log x = 1 / x, obtenemos:

Es decir, la probabilidad máxima (aproximadamente 27%) se alcanza en

Por si acaso, calculamos la segunda derivada:
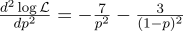
En el punto p = 0.7, es negativo, por lo que este punto es realmente el máximo de la función L.
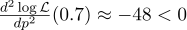
Y aquí está la densidad de probabilidad para el esquema de Bernoulli con
p = 0.7:
Ejemplo dos: ADC
Imaginemos que tenemos una cierta cantidad física constante que queremos medir, ya sea una longitud con una regla o un voltaje con un voltímetro. Cualquier medida da una
aproximación de esta cantidad, pero no la cantidad misma. Los métodos que describo aquí fueron desarrollados por Gauss a fines del siglo XVIII, cuando midió las órbitas de los cuerpos celestes.
Por ejemplo, si medimos el voltaje de la batería N veces, obtenemos N mediciones diferentes. ¿Cuál tomar? Eso es todo! Entonces, tengamos N cantidades Uj:
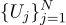
Suponga que cada medida Uj es igual a un valor ideal, más un ruido gaussiano, que se caracteriza por dos parámetros: la posición de la campana gaussiana y su "ancho". Aquí está la densidad de probabilidad:
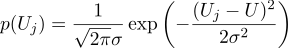
Es decir, teniendo N valores dados de Uj, nuestra tarea es encontrar dicho parámetro, U que maximice el valor de probabilidad. La credibilidad (de inmediato tomo el logaritmo) se puede escribir de la siguiente manera:
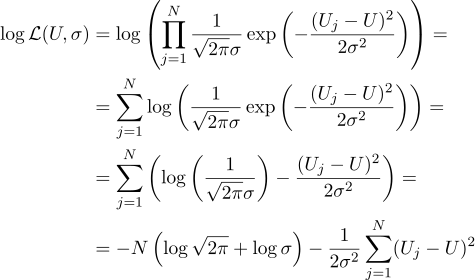
Bueno, entonces todo es estrictamente como antes, equiparamos a cero derivadas parciales con respecto a los parámetros que estamos buscando:
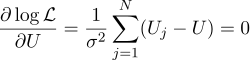
Encontramos que la estimación más probable de la cantidad desconocida U se puede encontrar como el promedio de todas las mediciones:
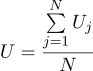
Bueno, el parámetro sigma más probable es la desviación estándar habitual:
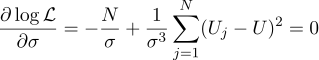

¿Valió la pena molestarse en obtener un promedio simple de todas las mediciones en la respuesta? Para mi gusto, valió la pena. Por cierto, promediar múltiples mediciones de un valor constante para aumentar la precisión de las mediciones es una práctica estándar. Por ejemplo, el
promedio de ADC . Por cierto, para este ruido gaussiano no es necesario, es suficiente que el ruido sea imparcial.
Ejemplo tres, y nuevamente unidimensional
Continuamos la conversación, tomemos el mismo ejemplo, pero lo complicamos un poco. Queremos medir la resistencia de cierta resistencia. Con la ayuda de una fuente de alimentación de laboratorio, podemos pasar un número estándar de amperios a través de ella y medir el voltaje que se necesitará para esto. Es decir, tendremos N pares de números (Ij, Uj) en la entrada de nuestro evaluador de resistencia.
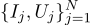
Dibuja estos puntos en la tabla; La ley de Ohm nos dice que estamos buscando la pendiente de la línea azul.
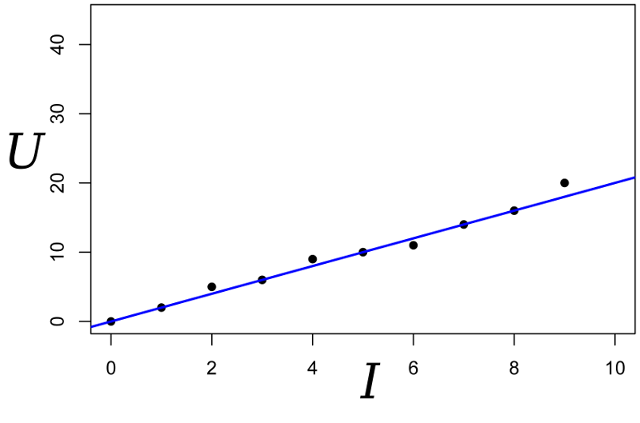
Escribimos la expresión para la probabilidad del parámetro R:
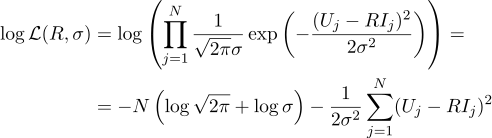
Y nuevamente, equiparamos a cero la derivada parcial correspondiente:
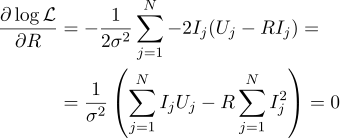
Entonces la resistencia R más plausible se puede encontrar mediante la siguiente fórmula:
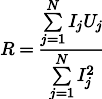
Este resultado ya es algo menos obvio que el promedio simple de todas las mediciones. Tenga en cuenta que si tomamos cien mediciones en la región de un amperio, y una medición en la región de un kilo amperio, entonces las cien mediciones anteriores prácticamente no afectarán el resultado. Recordemos este hecho, nos será útil en el próximo artículo.
Cuarto ejemplo: Volver a los mínimos cuadrados
Seguramente ya habrá notado que en los últimos dos ejemplos, maximizar el logaritmo de probabilidad es equivalente a minimizar la suma de los cuadrados del error de estimación. Veamos otro ejemplo. Tome la calibración de la romana usando pesas de referencia. Supongamos que tenemos N cargas de masa de referencia xj, cuélguelas en una romana y mida la longitud del resorte, obtenemos N longitudes de resorte yj:

La ley de Hooke nos dice que la extensión del resorte depende linealmente de la fuerza aplicada, y esta fuerza incluye el peso de los bienes y el peso del resorte mismo. Deje que la rigidez del resorte sea el parámetro
a , pero la tensión del resorte bajo su propio peso es el parámetro b. Entonces podemos escribir la expresión de la probabilidad de nuestras mediciones de esta manera (como antes, bajo la hipótesis del ruido de medición gaussiano):
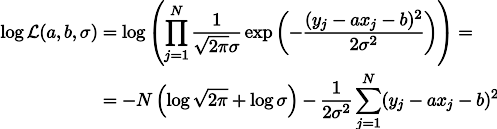
La maximización de probabilidad de L es equivalente a minimizar la suma de los cuadrados de los errores de estimación, es decir, podemos buscar el mínimo de la función S definida de la siguiente manera:
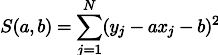
En otras palabras, estamos buscando una línea recta que minimice la suma de los cuadrados de las longitudes de los segmentos verdes:
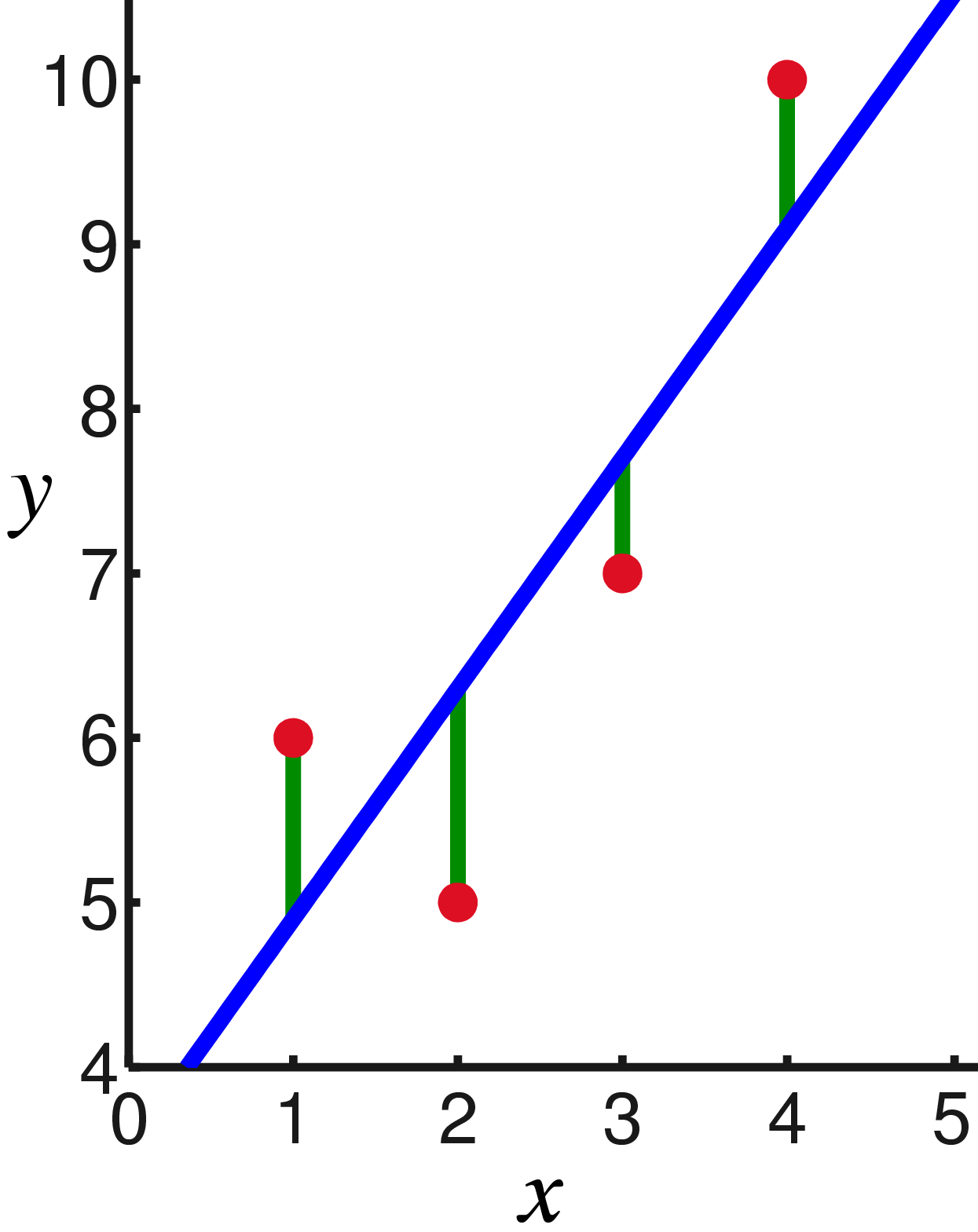
Bueno, entonces no hay sorpresas, establecemos derivadas parciales a cero:
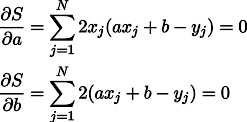
Obtenemos un sistema de dos ecuaciones lineales con dos incógnitas:
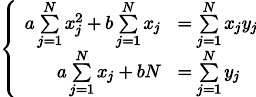
Recordamos el séptimo grado de la escuela y escribimos la solución:

Conclusión
Los métodos de mínimos cuadrados son un caso especial de maximizar la probabilidad para aquellos casos en que la densidad de probabilidad es gaussiana. En el caso de que la densidad sea (en absoluto) gaussiana, los mínimos cuadrados dan una estimación que difiere de la MLE (estimación de semejanza máxima). Por cierto, en un momento, Gauss planteó la hipótesis de que la distribución no juega un papel, solo la independencia de las pruebas es importante.
Como puede ver en este artículo, cuanto más se adentra en el bosque, más engorrosas son las soluciones analíticas para este problema. Bueno, sí, no estamos en el siglo XVIII, ¡tenemos computadoras! La próxima vez veremos un enfoque geométrico y, luego, programático para el problema de OLS, permanezca en la línea.