Me preparé durante mucho tiempo y recopilé material, espero que esta vez haya salido mejor. Dedico este artículo a los métodos básicos para resolver problemas de optimización matemática con limitaciones, por lo que si escuchaste que el método simplex es un método
muy importante , pero aún no sabes lo que hace, entonces este artículo probablemente te ayudará.
PD El artículo contiene fórmulas matemáticas agregadas por el editor de macros. Dicen que a veces no se muestran. También hay muchas animaciones en formato gif.
Preámbulo
El problema de la optimización matemática es un problema de la forma "Buscar en el conjunto
mathcalK el elemento
x∗ tal que para todos
x de
mathcalK realizado
f(x∗) leqf(x) ", Que en la literatura científica es probable que se escriba de esta manera
\ begin {array} {rl} \ mbox {minimizar} & f (x) \\ \ mbox {proporcionado} & x \ en \ mathcal {K}. \ end {array}
\ begin {array} {rl} \ mbox {minimizar} & f (x) \\ \ mbox {proporcionado} & x \ en \ mathcal {K}. \ end {array}
Históricamente, los métodos populares, como el descenso de gradiente o el método de Newton, solo funcionan en espacios lineales (y preferiblemente, simples, por ejemplo
mathbbRn ) En la práctica, a menudo hay problemas en los que necesita encontrar un mínimo que no esté en el espacio lineal. Por ejemplo, necesita encontrar el mínimo de alguna función en tales vectores
x=(x1, ldots,xn) para que
xi geq0 , esto puede deberse al hecho de que
xi denota la longitud de cualquier objeto. O por ejemplo, si
x representar las coordenadas de un punto que no debería ser más de
r de
y es decir
|x−y | leqr . Para tales problemas, el descenso de gradiente o el método de Newton ya no es directamente aplicable. Resultó que una clase muy grande de problemas de optimización está convenientemente cubierta por "restricciones", similares a las que describí anteriormente. En otras palabras, es conveniente representar el conjunto
mathcalK en forma de un sistema de igualdades y desigualdades
beginarraylgi(x) leq0, 1 leqi leqm,hi(x)=0, 1 leqi leqk. endarray
Problemas de minimización en un espacio de la forma
mathbbRn por lo tanto, comenzaron a llamarlos arbitrariamente "problema sin restricciones", y problemas sobre conjuntos definidos por conjuntos de igualdades y desigualdades, "problemas restringidos".
Técnicamente, absolutamente cualquier multitud
mathcalK puede representarse como una sola igualdad o desigualdad utilizando la función de
indicador , que se define como
I_ \ mathcal {K} (x) = \ begin {cases} 0, & x \ notin \ mathcal {K} \\ 1, y x \ in \ mathcal {K}, \ end {cases}
sin embargo, dicha función no tiene varias propiedades útiles (convexidad, diferenciabilidad, etc.). Sin embargo, a menudo se puede imaginar
mathcalK en forma de varias igualdades y desigualdades, cada una de las cuales tiene tales propiedades. La teoría básica se resume bajo el caso
\ begin {array} {rl} \ mbox {minimizar} & f (x) \\ \ mbox {proporcionado} & g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ end {array}
donde
f,gi - funciones convexas (pero no necesariamente diferenciables),
A - matriz. Para demostrar cómo funcionan los métodos, usaré dos ejemplos:
- Tarea de programación lineal
$$ display $$ \ begin {array} {rl} \ mbox {minimizar} & -2 & x ~~~ - & y \\ \ mbox {proporcionado} & -1.0 y ~ x -0.1 & ~ y \ leq -1.0 \ \ & -1.0 & ~ x + ~ 0.6 & ~ y \ leq -1.0 \\ & -0.2 & ~ x + ~ 1.5 & ~ y \ leq -0.2 \\ & ~ 0.7 & ~ x + ~ 0.7 & ~ y \ leq 0.7 \\ & ~ 2.0 & ~ x -0.2 & ~ y \ leq 2.0 \\ & ~ 0.5 & ~ x -1.0 & ~ y \ leq 0.5 \\ & -1.0 & ~ x -1.5 & ~ y \ leq - 1.0 \\ \ end {array} $$ display $$
En esencia, este problema consiste en encontrar el punto más alejado del polígono en la dirección (2, 1), la solución al problema es el punto (4.7, 3.5), el más "correcto" en el polígono). Pero el polígono mismo
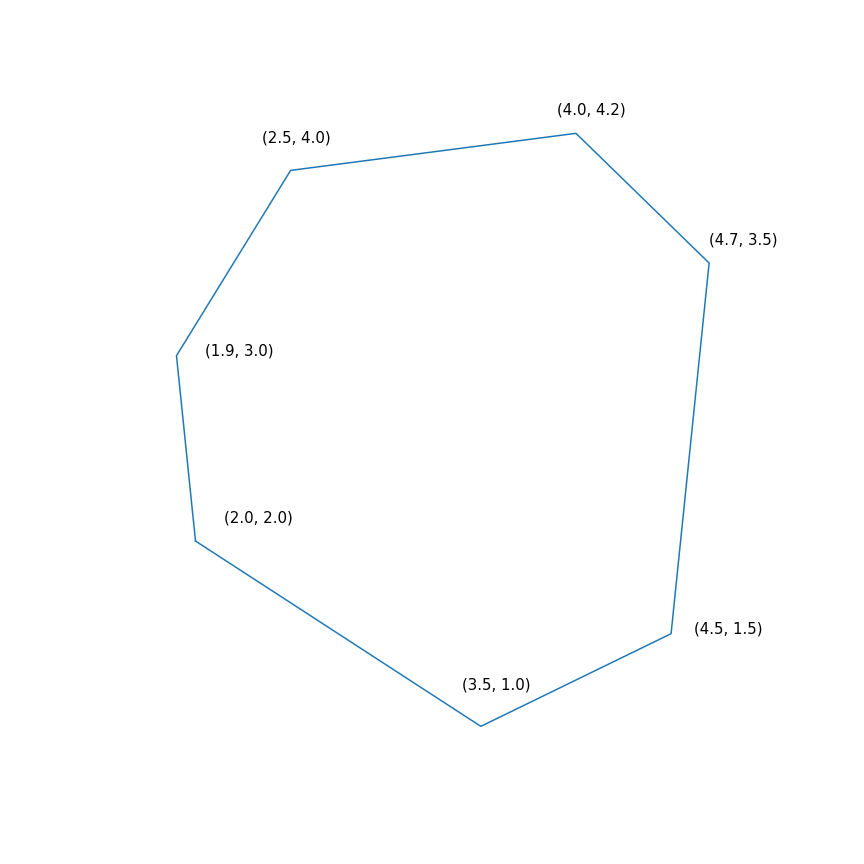
- Minimización de una función cuadrática con una restricción cuadrática
\ begin {array} {rl} \ mbox {minimizar} & 0.7 (x - y) ^ 2 + 0.1 (x + y) ^ 2 \\ \ mbox {proporcionado} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {array}
Método simplex
De todos los métodos que cubro con esta revisión, el método simplex es probablemente el más famoso. El método se desarrolló específicamente para la programación lineal y el único de los presentados logra la solución exacta en un número finito de pasos (siempre que se use la aritmética exacta para los cálculos, en la práctica este no suele ser el caso, pero en teoría es posible). La idea de un método simplex consta de dos partes:
- Los sistemas de desigualdades e igualdades lineales definen poliedros convexos multidimensionales (politopos). En el caso unidimensional, este es un punto, rayo o segmento, en el caso bidimensional, un polígono convexo, en el caso tridimensional, un poliedro convexo. Minimizar la función lineal es esencialmente encontrar el punto "más alejado" en una determinada dirección. Creo que la intuición debería sugerir que este punto más lejano debería ser un cierto pico, y de hecho es así. En general, para un sistema de m desigualdades en n espacio dimensional un vértice es un punto que satisface un sistema para el cual exactamente n de estas desigualdades se convierten en igualdades (siempre que entre las desigualdades no haya equivalentes). Siempre hay un número finito de tales puntos, aunque puede haber muchos de ellos.
- Ahora tenemos un conjunto finito de puntos, en términos generales, simplemente puede seleccionarlos y clasificarlos, es decir, hacer algo como esto: para cada subconjunto de n desigualdades, resuelva el sistema de ecuaciones lineales compiladas sobre las desigualdades elegidas, verifique que la solución se ajuste al sistema original de desigualdades y compárelo con otros puntos similares. Este es un método bastante simple, ineficiente pero de trabajo. El método simplex, en lugar de iterar, se mueve de arriba hacia arriba a lo largo de los bordes para que los valores de la función objetivo mejoren. Resulta que si un vértice no tiene "vecinos" en los que los valores de la función son mejores, entonces es óptimo.
El método simplex es iterativo, es decir, secuencialmente mejora ligeramente la solución. Para tales métodos, debe comenzar en alguna parte, en el caso general, esto se hace resolviendo un problema auxiliar
\ begin {array} {rl} \ mbox {minimizar} & s \\ \ mbox {proporcionado} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
Si para resolver este problema
x∗,s∗ tal que
s∗ leq0 luego ejecutado
gi(x∗) leqs leq0 de lo contrario, el problema original generalmente se da en un conjunto vacío. Para resolver el problema auxiliar, también puede usar el método simplex, pero se puede tomar el punto de partida
s= maxigi(x) con arbitrario
x . Encontrar el punto de partida puede llamarse arbitrariamente la primera fase del método, encontrar la solución al problema original puede llamarse arbitrariamente la segunda fase del método.
La trayectoria del método simplex de dos fases.La trayectoria se generó usando scipy.optimize.linprog.
Descenso de gradiente proyectivo
Sobre el descenso de gradiente, recientemente escribí un
artículo separado en el que también describí brevemente este método. Ahora este método es bastante animado, pero se está estudiando como parte de un
descenso de gradiente proximal más general. La idea misma del método es bastante banal: si aplicamos el descenso de gradiente a una función convexa
f , con la elección correcta de parámetros obtenemos un mínimo global
f . Si, después de cada paso del descenso del gradiente, se corrige el punto obtenido, tomando su proyección en un conjunto convexo cerrado
mathcalK , entonces como resultado obtenemos el mínimo de la función
f en
mathcalK . Bueno, o más formalmente, el descenso de gradiente proyectivo es un algoritmo que calcula secuencialmente
begincasesxk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1), endcases
donde
P mathcalK(x)= mboxargminy in mathcalK |x−y |.$
La última igualdad define el operador estándar de proyección sobre el conjunto, de hecho es una función que, según el punto
x calcula el punto más cercano al conjunto
mathcalK . El papel de la distancia juega aquí
| ldots | , vale la pena señalar que cualquier
norma puede usarse aquí, sin embargo, ¡las proyecciones con diferentes normas pueden diferir!
En la práctica, el descenso de gradiente proyectivo se usa solo en casos especiales. Su principal problema es que calcular la proyección puede ser aún más difícil que la original, y debe calcularse muchas veces. El caso más común para el cual es conveniente usar el descenso de gradiente proyectivo es "restricciones de caja", que tienen la forma
elli leqxi leqri, 1 leqi leqn.$
En este caso, la proyección se calcula de manera muy simple, para cada coordenada resulta
[P _ {\ mathcal {K}} (x)] _ i = \ begin {cases} r_i, & x_i> r_i \\ \ ell_i, & x_i <\ ell_i \\ x_i, & x_i \ in [\ ell_i, r_i ] \ end {cases}
El uso del descenso de gradiente proyectivo para problemas de programación lineal no tiene sentido, sin embargo, si haces esto, se verá más o menos así
Trayectoria de descenso de gradiente proyectiva para un problema de programación lineal Y aquí está la trayectoria del descenso de gradiente proyectivo para el segundo problema, si
elija un tamaño de paso grande y si
elige un pequeño tamaño de escalón Método elipsoide
Este método es notable porque es el primer algoritmo polinomial para problemas de programación lineal; puede considerarse una generalización multidimensional del
método de bisección . Comenzaré con un
método más general
para separar el hiperplano :
- En cada paso del método, hay un conjunto que contiene la solución al problema.
- En cada paso, se construye un hiperplano, después de lo cual todos los puntos que se encuentran en un lado del hiperplano seleccionado se eliminan del conjunto y se pueden agregar algunos puntos nuevos a este conjunto
Para problemas de optimización, la construcción del "hiperplano de separación" se basa en la siguiente desigualdad para las funciones convexas
f(y) geqf(x)+ nablaf(x)T(y−x).$
Si arreglar
x , entonces para una función convexa
f medio espacio
nablaf(x)T(y−x) geq0 contiene solo puntos con un valor no menor que en un punto
x , lo que significa que se pueden cortar, ya que estos puntos no son mejores que los que ya hemos encontrado. Para los problemas con las restricciones, también puede deshacerse de los puntos que se garantiza que violan una de las restricciones.
La versión más simple del método de hiperplano de separación es simplemente cortar los medios espacios sin agregar ningún punto. Como resultado, en cada paso tendremos un cierto poliedro. El problema con este método es que es probable que el número de caras del poliedro aumente de un paso a otro. Además, puede crecer exponencialmente.
El método elipsoide en realidad almacena un elipsoide en cada paso. Más precisamente, después de que se construye el hiperplano, se construye un elipsoide de volumen mínimo, que contiene una de las partes del original. Esto se puede lograr agregando nuevos puntos. Un elipsoide siempre se puede definir mediante una matriz positiva definida y un vector (centro de un elipsoide) de la siguiente manera
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \}. $
La construcción de un elipsoide mínimo en volumen, que contiene la intersección del medio espacio y otro elipsoide, se puede hacer usando
fórmulas moderadamente engorrosas . Desafortunadamente, en la práctica, este método seguía siendo tan bueno como el método simplex o el método de punto interno.
Pero en realidad cómo funciona para
y para
Método de punto interior
Este método tiene una larga historia de desarrollo, uno de los primeros requisitos previos apareció aproximadamente al mismo tiempo que se desarrolló el método simplex. Pero en ese momento todavía no era lo suficientemente efectivo como para ser utilizado en la práctica. Más tarde, en 1984, se desarrolló una
variante del método específicamente para la programación lineal, que era buena tanto en teoría como en la práctica. Además, el método de punto interno no se limita solo a la programación lineal, a diferencia del método simplex, y ahora es el algoritmo principal para problemas de optimización convexa con restricciones.
La idea básica del método es reemplazar las restricciones con una multa en forma de la llamada
función de barrera . Función
F:Int mathcalK rightarrow mathbbR llamada la
función de barrera para el conjunto
mathcalK si
F(x) rightarrow+ infty mboxatx rightarrow partial mathcalK.$
Aqui
Int mathcalK - dentro
mathcalK ,
parcial matemáticaK - frontera
mathcalK . En lugar del problema original, se propone resolver el problema.
mboxminimizarporx varphi(x,t)=tf(x)+F(x).$
F y
varphi dado solo en el interior
mathcalK (de hecho, de aquí viene el nombre), la propiedad de la barrera asegura que
varphi al menos
x existe Además, cuanto más
t cuanto mayor es el impacto
f . En condiciones razonablemente razonables, puede lograr eso si apunta
t hasta el infinito entonces el mínimo
varphi convergerá a la solución del problema original.
Si el conjunto
mathcalK dado como un conjunto de desigualdades
gi(x) leq0, 1 leqi leqm entonces la opción estándar de la función de barrera es la
barrera logarítmicaF(x)=− summi=1 ln(−gi(x)).$
Puntos mínimos
x∗(t) las funciones
varphi(x,t) por diferentes
t forma una curva, que generalmente se llama la
ruta central , el método del punto interno, por así decirlo, está tratando de seguir esta ruta. Así es como se ve
Ejemplos de programación lineal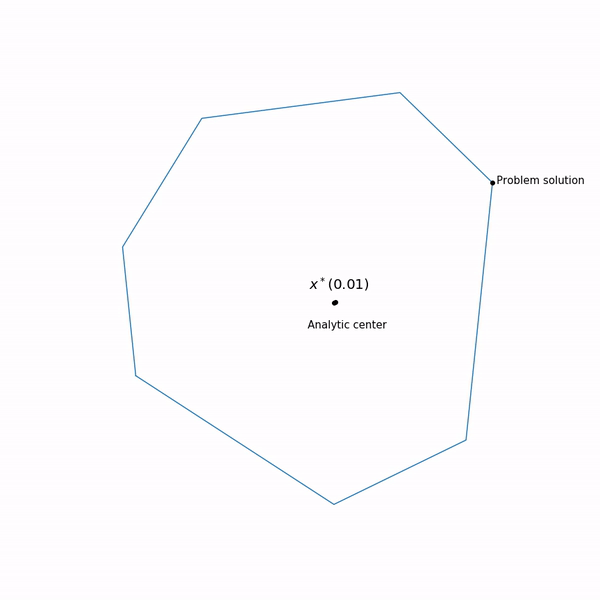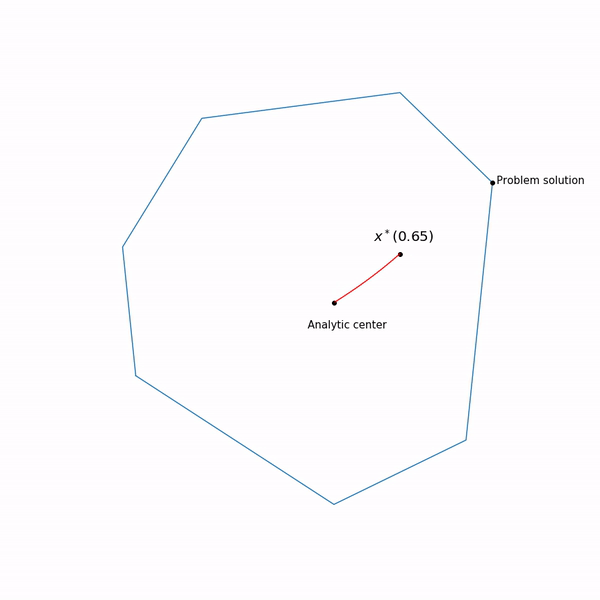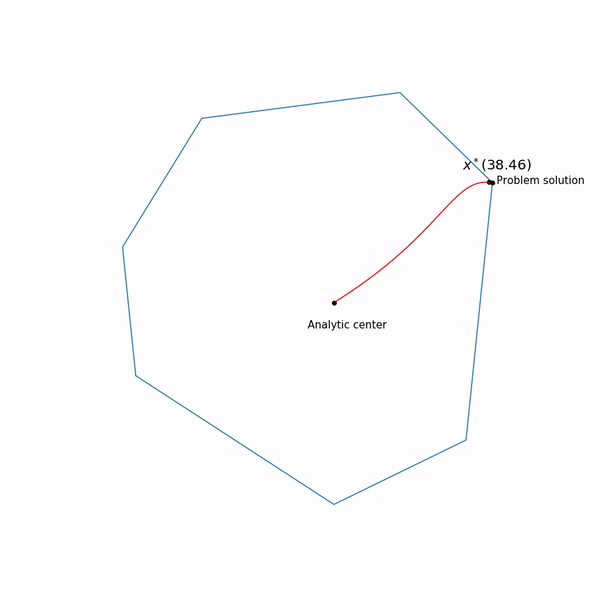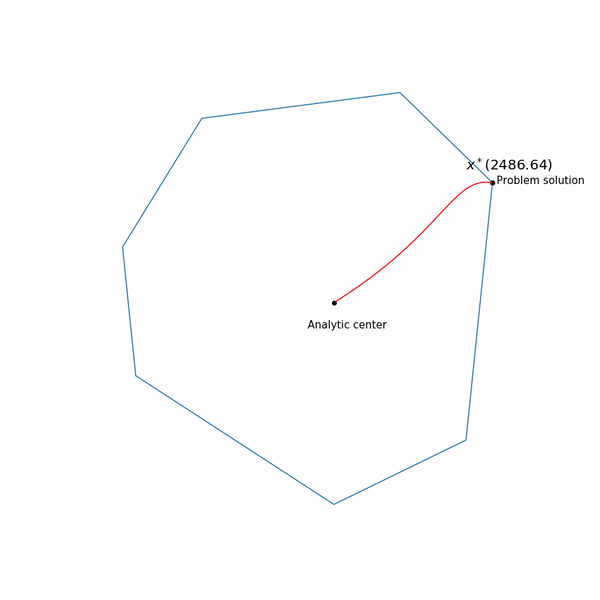 El centro analítico
El centro analítico es solo
x∗(0) Finalmente, el método de punto interno tiene la siguiente forma
- Seleccione una aproximación inicial x0 , t0>0
- Elija una nueva aproximación usando el método de Newton
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- Click para ampliar t
tk+1= alphatk, alpha>1
El uso del método de Newton es muy importante aquí: el hecho es que con la elección correcta de la función de barrera, el paso del método de Newton genera un punto
que permanece dentro de nuestro conjunto , experimentamos, no siempre se rinde de esta forma. Y finalmente, así es como se ve la trayectoria del método de punto interno
Tarea de programación linealEl punto negro que rebota es
x∗(tk) es decir punto al cual estamos tratando de acercarnos al paso del método de Newton en el paso actual.
Problema de programación cuadrática