En 2018, celebramos tres concursos Yandex.Blitz: aprendizaje automático, desarrollo móvil y front-end. La tercera competencia se realizó recientemente , ¡felicidades a los ganadores! Mientras tanto, queremos volver al segundo de ellos, donde se propusieron tareas en la unión de algoritmos y software de escritura para Android / iOS. Los candidatos para el puesto de desarrollador móvil en Yandex se beneficiarán de la experiencia en la resolución de tales problemas. Lea el análisis detallado de algunos de ellos. Y si no participó en el Blitz, entonces es mejor que primero intente resolverlos usted mismo .

La tarea de "suministro de gas"
| Entrar | Conclusión | Límite de tiempo | Límite de memoria |
|---|
| entrada estándar o input.txt | salida estándar o salida.txt | 15 segundos | 15 megabytes |
Nika está desarrollando una aplicación para altos directivos en una importante compañía de gas para ayudarlos a planificar la producción.
La compañía está considerando n campos que están d 1 ... d i ... d n kilómetros de distancia de la tubería y puede producir v 1 ... v i ... v n unidades de gas. Se vende una licencia por separado para cada campo: las licencias son s 1 ... s i ... s n .
Para conectar los campos con la carretera, debe construir tuberías. Un contratista que puede colocar m diferentes tipos de tuberías ayuda a esta empresa. Las tuberías difieren entre sí en longitud (l 1 ... l i ... l m ) y precio (p 1 ... p i ... p m ). Se pueden combinar entre sí como quieras.
La compañía tiene k monedas y quiere obtener la mayor cantidad de gasolina posible.
¿Cuánto podrá producir la compañía si le da al contratista pedidos óptimos?
La tubería puede ser más larga que la distancia del campo a la tubería.
La primera línea contiene un número entero k ≤ 10 5 .
La segunda línea contiene un número entero n ≤ 15.
Las siguientes n líneas contienen tres enteros d i ≤ 100, v i ≤ 100 y s i ≤ 100.
Los números están separados por un espacio.
La siguiente línea contiene un número entero m ≤ 15.
Las siguientes m líneas contienen dos enteros l i ≤ 100 y p i ≤ 100. Los números están separados por un espacio.
La única línea con la respuesta.
Ejemplos
| Entrar | Conclusión |
116
3
58 7 50
81 71 56
52 57 31
3
47 9
1 25
18 61 | 57 |
Analizando
Para empezar, definamos la notación. Que haya una clase de objetos Depósito (depósito) con parámetros $ en línea $ Dd_ {i} $ en línea $ (lejanía) $ en línea $ Dv_ {i} $ en línea $ (volumen de producción) y $ en línea $ Ds_ {i} $ en línea $ (costo de la licencia). Los objetos de índice de este tipo serán la variable i. También hay una clase de objeto Pipeliner con parámetros $ en línea $ PPl_ {j} $ en línea $ (la longitud de la tubería que el contratista puede construir) y $ en línea $ PPp_ {j} $ en línea $ (precio de esta tubería), índice a través de j. Los participantes del bombardeo muchas veces preguntaron si un tipo de tubería se puede usar dos veces. Se supone que no, y este ejemplo lo muestra claramente. Entonces, según los términos de esta tarea, aceptar $ en línea $ D_ {i} = {0, 1} $ en línea $ (elija un campo o no) y $ en línea $ PP_ {j} = {0, 1} $ en línea $ (elija un contratista o no), puede realizar una tarea de programación lineal:
$ en línea $ \ sum \ limits_ {i} D_ {i} * Dv_ {i} \ rightarrow max \\ \ sum \ limits_ {i} D_ {i} * Ds_ {i} + \ sum \ limits_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ sum \ limits_ {i} D_ {i} * Dd_ {i} \ leq \ sum \ limits_ {j} PP_ {j} * PPl_ {j} \\ D_ { i} = {0, 1}, PP_ {j} = {0, 1} $ en línea $
Se puede resolver, por ejemplo, mediante el método simplex. Sin embargo, según los términos de la tarea, estamos obligados a devolver solo el volumen de producción máximo (es decir, el valor de la función objetivo) y no es necesario indicar qué campos y qué contratistas deben seleccionarse. Junto con las restricciones en la condición, el problema puede resolverse mediante el método de programación dinámica construyendo una tabla dp [longitud] [dinero], donde longitud es la longitud de la tubería, el dinero es dinero. Después de la construcción correcta de la tabla, es suficiente para encontrar el valor máximo en ella, que será la respuesta. Las limitaciones de memoria de la tarea son suficientes para construir.
La tarea de "Torres e IA"
| Entrar | Conclusión | Límite de tiempo | Límite de memoria |
|---|
| entrada estándar o input.txt | salida estándar o salida.txt | 1 segundo | 64 megabytes |
Artem está desarrollando inteligencia artificial jugando un juego móvil competitivo. Las reglas del juego son simples.
Antes de los jugadores hay n torres con una altura de c 1 ... c i ... c n . En su turno, el jugador puede romper una de las torres para obtener varias torres más pequeñas. Los jugadores tienen miedo de confundirse en las torres, por lo que acordaron una limitación: después de la separación, no se deben obtener dos torres de la misma altura. Por ejemplo, una torre con una altura de 7 se puede dividir en (1, 2, 4), pero no en (1, 3, 3). La altura es siempre un número entero.
Pierde al que no tiene torres que pueden ser destruidas.
Artem tiene un amigo muy inteligente que juega de manera óptima: es con él que lucha la inteligencia artificial de Artem. Para evaluar el trabajo de la IA, Artyom necesita saber si el robot debería ganar si ambos jugadores actúan de manera óptima. Ayúdalo con esto.
El hombre siempre camina primero. Jugará con juegos de AI k.
La primera línea contiene un entero k <500.
Esto es seguido por k bloques de dos líneas.
La primera línea de cada bloque es un número entero 0 <n ≤ 50.
La segunda línea de cada bloque tiene n enteros 0 <c i ≤ 50. Los números están separados por espacios.
k líneas, cada una de las cuales contiene verdadero o falso, dependiendo de si una persona gana el juego.
Ejemplos
| Entrar | Conclusión |
2
1
4 4
2
1 1 | falso
falso |
Analizando
El juego de la torre propuesto es un juego final equitativo para dos jugadores en el que es imposible dibujar.
Por lo tanto, la victoria de un jugador en particular en el juego está determinada por el estado del juego y el orden de los movimientos de los dos jugadores. Para los lectores que están familiarizados con la teoría de juegos, es obvio que cualquiera de los juegos iguales de dos jugadores es en realidad equivalente al juego "él", lo que significa nuestro juego también.
Aquí hay una breve descripción de él: un juego ( enlace a la fuente; haga clic en él para obtener una revisión detallada):
Hay varias pilas, cada una de las cuales tiene varias piedras. En un movimiento, el jugador puede tomar cualquier cantidad de piedras que no sea cero de cualquier pila y tirarlas. En consecuencia, se produce una pérdida cuando no quedan más movimientos, es decir, Todas las pilas están vacías.
Entonces, el estado del juego "él" se describe de manera única por un conjunto desordenado de números naturales. En un movimiento, se permite reducir estrictamente cualquiera de los números (si como resultado el número se convierte en cero, entonces se elimina del conjunto).
La solución para el juego de nim es encontrar la suma xor del tamaño de los montones, y solo si esta suma no es cero, podemos decir claramente que estamos en un estado ganador.
Además, el teorema de Sprag-Grandi viene en nuestra ayuda, que establece que el estado U de cualquier juego igual de dos jugadores puede asociarse con un puñado de juegos de él de tamaño X. Tan pronto como una función que especifique el mapeo de los estados de nuestro juego para él sea un juego, la solución al problema se reducirá. para resolverlo, un juego que ya se conoce.
Tarea "Indicación de calificación"
| Entrar | Conclusión | Límite de tiempo | Límite de memoria |
|---|
| entrada estándar o input.txt | salida estándar o salida.txt | 1 segundo | 64 megabytes |
Galya está desarrollando un agregador de revisión. Ella decidió designar las calificaciones de las instituciones con la ayuda de estrellas de siete puntas.
El sistema de representación de entrada recibe un rectángulo de altura h y ancho w, cuya esquina superior izquierda se encuentra en el punto (x, y). Se debe dibujar una estrella de acuerdo con las siguientes reglas:
- El tamaño de una estrella está determinado por el ancho o la altura del rectángulo, es decir, más pequeño. (Ver los dibujos).
- Si una de las dimensiones del rectángulo es mayor que la dimensión correspondiente de la estrella, la estrella debe centrarse en esa dimensión.
- La estrella está apuntando hacia arriba.
El sistema de representación espera las coordenadas de los vértices de la estrella del código de Gali. Ayuda a Gale a calcularlos.
Para construir una estrella de siete puntas, Galya toma el contorno exterior de la figura obtenida conectando los vértices de un heptágono regular a través de uno. En el sistema de coordenadas, el eje X se dirige de izquierda a derecha, el eje Y de arriba a abajo. El programa Gali no se bloquea, recibiendo valores incorrectos de ancho y alto como entrada.
Una sola línea contiene enteros x, y, w y h, separados por espacios.
Ejemplo: la entrada 150 0 50 100 denota un rectángulo con un ancho de 50 puntos, una altura de 100 puntos y con la esquina superior izquierda en el punto (150, 0).
La única línea que contiene 28 números separados por espacios son las coordenadas de los vértices de la estrella, comenzando desde la parte superior y luego en sentido horario. Los números deben redondearse al entero más cercano. Vea un ejemplo de la salida y una ilustración del problema antes de continuar con la solución.
Ejemplo: la salida de tres puntos (1, 2), (3, 4), (5, 6) debería verse así: 1 2 3 4 5 6.
Ejemplos
| Entrar | Conclusión |
0 0 100 100 | 50 1 65 21 90 21 85 45100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21 |
Notas
La precisión requerida es de 10 dígitos significativos.
Sistema de coordenadas: el eje X se dirige de izquierda a derecha, el eje Y de arriba a abajo:
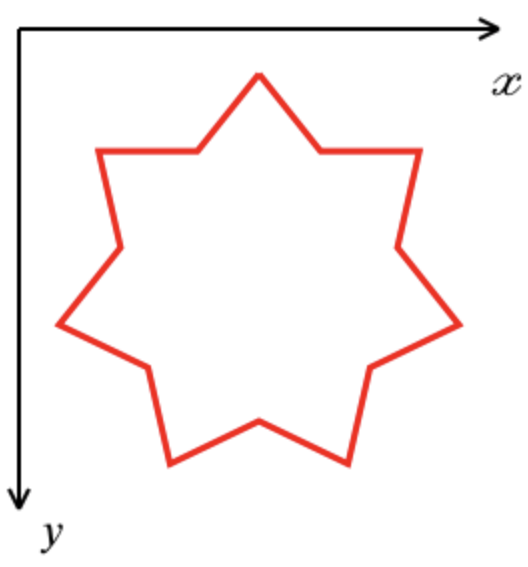
- Orden de vértice esperado:
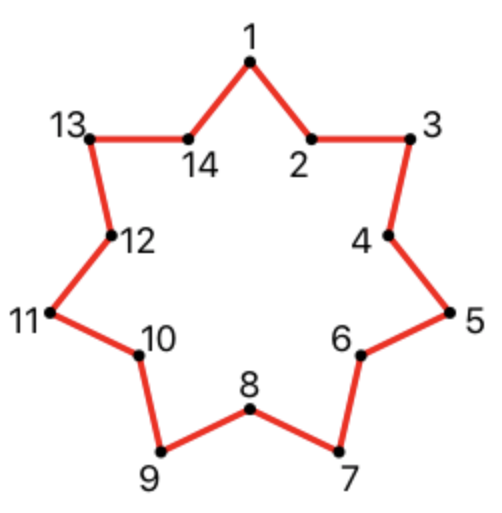
Ejemplos de estrellas inscritas:
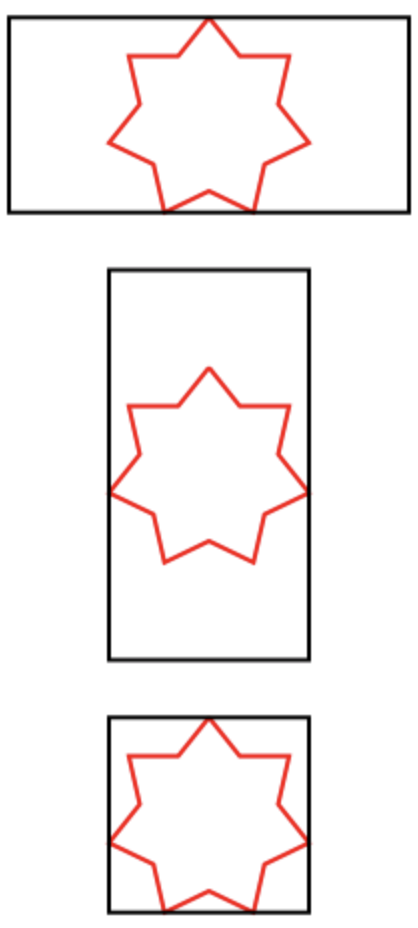
Analizando
La solución al problema se reduce a tres etapas: construir una estrella de referencia con la orientación deseada en el espacio, escalar los puntos resultantes, calcular y aplicar el desplazamiento.
Construyendo una estrella
La forma más fácil es construir una estrella inscrita en un círculo con un radio unitario centrado en el origen. Los puntos de los vértices externos se calculan mediante trigonometría trivial, pero con los internos la tarea es un poco más complicada. Se pueden encontrar al menos de dos maneras. Una forma más fácil es encontrar las intersecciones de los segmentos que conectan los vértices exteriores. Más complicado es encontrar una fórmula para calcular el radio de un círculo inscrito a partir del radio de un círculo circunscrito. La forma más fácil de hacer esto es primero, por ejemplo, para una estrella de 5 puntas, y generalizada a la estrella de N puntas con un espacio arbitrario entre los vértices conectados.
Escalamiento
En todos los casos, se da el tamaño en el que necesitamos ajustar la estrella. Por lo tanto, necesitamos escalar los puntos obtenidos para que la distancia desde el extremo izquierdo al extremo derecho no exceda el ancho especificado, y la distancia desde el más alto al más bajo no exceda la altura especificada. Tomamos los factores de escala para llevar el ancho y la altura a los valores deseados, y seleccionamos el más pequeño. Como construimos prudentemente una estrella de referencia con el centro en el origen, es suficiente simplemente multiplicar las coordenadas de cada punto por el coeficiente seleccionado.
Offset
Lo último que queda es mover nuestros puntos para que la estrella esté dentro de los cuadros dados. Los datos de entrada de todas las opciones se pueden reducir a un cuadro delimitador con una coordenada dada de la esquina superior izquierda. Aquí todo es simple: tomamos el punto más alto de los resultados obtenidos en la última etapa, consideramos la diferencia de su coordenada y con la coordenada y de la esquina superior izquierda y desplazamos todos los puntos verticalmente por el valor obtenido. Hacemos lo mismo con la coordenada x, simplemente no tomamos el punto más alto, sino el más a la izquierda. Hay un toque final: centrar la estrella en este rectángulo.
Otras acciones dependen de qué coeficiente elegimos en la etapa anterior:
- si se escala en altura, tomamos la diferencia entre el ancho del rectángulo y la distancia desde el punto izquierdo al extremo derecho;
- si se amplía en ancho, tomamos la diferencia entre la altura del rectángulo y la distancia desde el punto más alto al más bajo.
Divida el valor obtenido por 2 y desplace los puntos según la medida correspondiente. Respuesta recibida
La tarea "Rotación y escala de un círculo"
| Entrar | Conclusión | Límite de tiempo | Límite de memoria |
|---|
| entrada estándar o input.txt | salida estándar o salida.txt | 1 segundo | 64 megabytes |
Vika está desarrollando un editor de gráficos para teléfonos inteligentes y tabletas. Ella quiere darle al usuario la oportunidad de rotar un círculo en la pantalla con dos dedos y cambiar su tamaño, así:
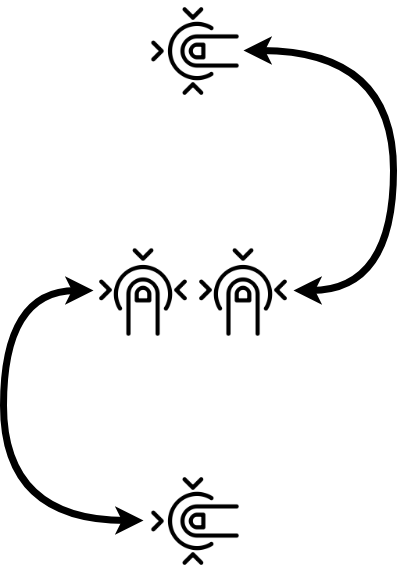
La figura gira en el mismo ángulo que gira el segmento que conecta los dedos. El tamaño de la figura cambia en proporción a la longitud del segmento. Primero, se gira la figura y luego se cambia su tamaño. Inicialmente, el círculo tiene coordenadas (x, y) y radio r. Se proporciona una lista de eventos táctiles que describen el gesto del usuario. Ayuda a Vika a calcular las coordenadas finales del centro del círculo y su radio. El círculo gira en relación con el punto (a, b).
La descripción del evento táctil contiene la identificación del dedo, las coordenadas y el tipo de evento. El primer dedo que el usuario adjunto recibe la identificación 0, la segunda identificación 1, y así sucesivamente.
Un ejemplo:
0 337 490 ACTION_DOWN: esto significa que con el dedo 0 en el punto (337, 490) se produjo el evento ACTION_DOWN.
Los eventos táctiles son de los siguientes tipos:
- ACTION_DOWN: el usuario aplicó el primer dedo a la pantalla en un punto determinado.
- ACTION_POINTER_DOWN: el usuario aplicó un segundo dedo a la pantalla en un punto determinado.
- ACTION_MOVE: el usuario ha movido su dedo a un punto determinado.
- ACTION_POINTER_UP: el usuario movió el segundo dedo al punto especificado y lo soltó.
- ACTION_UP: el usuario movió el primer dedo al punto especificado y lo soltó.
- ACTION_CANCEL: gesto anulado por el usuario.
La primera línea contiene los números x, y, yr, separados por espacios. La segunda línea contiene los números a y b, separados por espacios. Las siguientes líneas contienen eventos táctiles consecutivos.
La única línea con coordenadas y radio. Los números están separados por espacios.
Ejemplo
| Entrar | Conclusión |
252 194 78
445,559
0 337,490 ACTION_DOWN
1,599,490 ACTION_POINTER_DOWN
1,576,564 ACTION_MOVE
1,552,590 ACTION_MOVE
0 407,375 ACTION_MOVE
1 505 615 ACTION_MOVE
1 482 620 ACTION_MOVE
0 477 360 ACTION_MOVE
1,435,616 ACTION_MOVE
1,411,607 ACTION_MOVE
0 547 386 ACTION_MOVE
1 364 548 ACTION_POINTER_UP
0 571 387 ACTION_UP | 831 704 73 |
Notas
Al mostrar el resultado, es necesario redondear todos los valores de punto flotante a un valor entero de acuerdo con las reglas de redondeo matemático.
Analizando
A pesar de que el gesto parece complicado, se puede dividir en dos componentes: rotación y escala. Para rotar la figura, necesitamos calcular el ángulo de rotación, que se puede obtener usando la siguiente fórmula:
a = atan2 (prevTouchX2 - prevTouchX1, prevTouchY2 - prevTouchY1) - atan2 (currentTouchX2 - currentTouchX1, currentTouchY2 - currentTouchY1).
Una vez recibido el ángulo de rotación, debe girar la figura en sí, lo que se reduce a girar cada punto de la figura por el ángulo de rotación. Después de rotar la figura, necesitamos escalarla. Escalar una figura es bastante trivial. Es necesario recordar la distancia entre el primer y el segundo dedo al recibir el evento ACTION_POINTER_DOWN para el segundo dedo, después de lo cual, al rastrear la distancia entre los dos primeros dedos, puede calcular el coeficiente por el cual necesita escalar la figura.
La tarea "Construcción de carreteras"
| Entrar | Conclusión | Límite de tiempo | Límite de memoria |
|---|
| entrada estándar o input.txt | salida estándar o salida.txt | 1 segundo | 64 megabytes |
En un juego móvil, el personaje principal construye una base en un planeta distante. Comienza con el perímetro: torres conectadas por paredes láser directas. Los arquitectos de la sede le envían un plano que muestra n torres con coordenadas (x 1 , y 1 ) ... (x i , y i ) ... (x n , y n ). Desde el punto de vista de la defensa de base, no tiene sentido colocar tres o más torres vecinas en una línea recta. Sin embargo, los arquitectos del personal a veces colocan las torres de esta manera, por lo que el propio jugador tiene que quitar las torres intermedias adicionales.
Habiendo terminado con el perímetro, el héroe comienza a equipar la base desde el interior. Quiere construir k caminos entre las torres: el camino puede conectar dos torres no adyacentes, pero no puede cruzar otro camino o muro. Todos los caminos que quieras pueden salir de una torre.
El héroe tiene p robots de carretera. Para elegir el plan de construcción de carreteras óptimo, el héroe les indica que clasifiquen todas las opciones posibles. Los robots comienzan a trabajar simultáneamente y una y otra vez al mismo tiempo brindan opciones únicas para la ubicación de las carreteras. Si antes de la siguiente iteración resulta que quedan menos opciones que robots, los robots adicionales se liberan y se envían a la cocina para cocinar la cena. Los robots restantes terminan las últimas opciones y se apagan.
Si resulta que puedes pavimentar el camino fuera de la base, el héroe declara la base insegura y vuela lejos del planeta.
¿Cuántos robots trabajarán en la cocina?
La primera línea contiene tres enteros 4 ≤ n ≤ 10 7 , 1 ≤ k ≤ ny un número primo 105 <p <11 × 104. Los números están separados por espacios.
Las siguientes n líneas contienen dos enteros 0 <x i , y i <109. Los números están separados por espacios.
La única línea con la respuesta. Si la base no es segura, imprima −1.
Ejemplo 1
| Entrar | Conclusión |
4 1 101363
0 0
1 0
1 1
0 1 | 101361 |
Hay dos formas de pavimentar el único camino: (0, 0) - (1, 1) y (1, 0) - (0, 1). Dos robots se ocuparán de ellos, y el resto irá a la cocina: p - 2 = 101 361.
Ejemplo 2
| Entrar | Conclusión |
4 1 101363
1 0
2 0
0 1
1 2 | -1 |
Aquí puede construir un camino entre (1, 0) - (0, 1), y esto está fuera de la base. El héroe reconoce la base como insegura, la respuesta es -1.
Ejemplo 3
| Entrar | Conclusión |
4 1 101363
0 0
1 0
2 0
0 1 | 101363 |
Las torres (0, 0), (1, 0) y (2, 0) están en la misma línea, por lo que el héroe no construirá la torre central (1, 0). No se puede pavimentar ningún camino, por lo tanto, todos los robots irán inmediatamente a la cocina: p = 101 363.
Analizando
Dividimos la solución del problema en tres pasos.
El primer paso es determinar para el conjunto de datos de vértices de entrada si el polígono es convexo y, de ser así, cuántos vértices reales tiene. Un polígono es convexo si todos sus vértices están ubicados en un lado de la línea que soporta cualquier borde. Por cada triple de vértices adyacentes $ en línea $ (x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1}) $ en línea $ construir un par de vectores $ en línea $ ab = ((x_ {i-1}, y_ {i-1}), (x_ {i}, y_ {i})) y bc = ((x_ {i}, y_ {i}), (x_ {i + 1}, y_ {i + 1})) $ en línea $ y calcule el signo de la expresión ab.x bc.y - bc.x ab.y.Si la expresión es 0, entonces los vértices se encuentran en una línea recta y, según la condición del problema, la torre que se encuentra en el vértice central desaparece, reduciendo el número total de torres. Si para todos los triples de vértices, el signo del producto es 0 o siempre el mismo, vaya al segundo paso; de lo contrario, consideramos que la base no es segura e imprimimos la respuesta -1.
Segundo paso El número de métodos para construir k diagonales disjuntas dentro de un N-gon convexo es , pero necesitamos calcular la expresión p - V mod p, donde p es primo.
Imagina N! como , donde el mayor factor común es a, y p gcd (a, p) = 1.
Si , , p p.
= 0 mod p.
, a b mod p = (a mod p ) (b mod p) mod p, mod p = mod p p.
Tercer paso n! 1 2 … p (p+1) ... 2p (2p+1) ..., (p+1) ... (2p-1) mod p = 1 2 ...(p-1)=(p-1)!.. , n mod p = ( k (n mod p)!)mod p, k = floor(n/p).
« »
| Conclusión | | |
|---|
| input.txt | output.txt | 10 | 224 |
n , . t 1 … t i … t n , d i - i- .
, , . , — , — , , . .
: , , . .
; , . , .
, ?
1 < n ≤ 3 × 10 3 .
n 0 ≤ t i ≤ 10 4 0 ≤ d i ≤ 10 4 . .
. — .
| Conclusión |
5 5
2 2
1 1
3 4
1 10
1 2 | 10.25000000 |
, . k=1 , , .
() , . 1,5 , , . , .
« »
| Conclusión | | |
|---|
| input.txt | output.txt | 2 | 64 |
2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .
, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].
, . . , , .
, ?
n ≤ 500. n x y. .
. — .
Ejemplo 1
| Conclusión |
4 4
100 100
200 100
200 200
100 200 | 0.000000 |
Ejemplo 2
| Conclusión |
6 6
167 84
421 84
283 192
433 298
164 275
320 133 | 326.986753 |
, , . « » : — . : , ( ) .
, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .
, , — , . (, , ):
- ( );
- : , - ;
- ( , 10-5 );
- even-odd rule — ;
- : 180 .
«DNA»
| Conclusión | | |
|---|
| input.txt | output.txt | 8 | 128 |
, . , , . n . , . : A, T, G C. . .
n. n . . 6⋅10 6 .
. . . . . , .
( , ):
5 5
TTT
GAAGCT
CAAT
AGA
AGGCA
:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA
, . — , — . , . . , .
, .
«QR Quest»
| Conclusión | | |
|---|
| input.txt | output.txt | 1 | 64 |

t, . t n i , .
t , .
Ejemplo 1
| Conclusión |
4 4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 | 0 0
13
15
5 5 |
Ejemplo 2
| Conclusión |
4 4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 | 3
9 9
2
7 7 |
, . QR- , . - .
Se ingresaron un total de ocho números: las coordenadas de las celdas en estas tablas, es decir, 4 pares con las coordenadas de la columna y la fila. Era necesario adivinar qué operación se realizó con estas celdas y de qué tabla una celda extra.
Usando manipulaciones simples, se podría verificar que esta es la suma xor para cuatro celdas de las tablas A, B y C, abordadas por los índices a 0 ... a 7 :
R = A [a 0 , a 1 ] ^ B [a 2 , a 3 ] ^ B [a 4 , a 5 ] ^ C [a 6 , a 7 ].