Un logro matemático importante fue la hipótesis de Zimmer encontrada por un pequeño equipo de investigadores.
Para rejillas en dimensiones superiores de simetría, no siempre es posible transferir a dimensiones inferiores al rangoEl éxito de Robert Zimmer se puede definir de muchas maneras. Como
presidente de la Universidad de Chicago desde 2006, llegó a los titulares, encontrando cantidades de nueve cifras para financiar y publicar
artículos en apoyo de la libertad de expresión en el campus. Pero antes de convertirse en presidente de la universidad, era matemático. Y mucho tiempo después de dejar una investigación seria, el plan de investigación que lanzó finalmente da sus resultados.
Hace un año, tres matemáticos
probaron la hipótesis de Zimmer relacionada con circunstancias en las que los espacios geométricos tienen simetrías de cierto tipo. Su prueba se ha convertido en uno de los mayores logros matemáticos de los últimos años. Pone fin a la pregunta que surgió ante Zimmer durante su intensa actividad mental a fines de los años setenta y principios de los ochenta.
"Diría que me fui a la cama cinco años pensando en esta tarea, todas las noches, así que estaba obsesionada con ella y es genial ver cómo la gente la resolvió", dijo Zimmer.
Por lo general, cuanto mayor es el espacio de dimensión geométrica, más simetrías puede tener. Esto se puede imaginar al estudiar un círculo existente en un plano bidimensional y una bola que se extiende en tres dimensiones: hay más formas de rotar la bola que formas de rotar un círculo. Las dimensiones adicionales de la bola crean simetrías adicionales.
La conjetura de Zimmer se refiere a simetrías de un tipo especial conocido como redes de alto rango. Ella pregunta si la medición del espacio geométrico limita el uso de simetrías de este tipo. Los autores del nuevo trabajo -
Aaron Brown y
Sebastian Hurtado-Salazar de la Universidad de Chicago y
David Fisher de la Universidad de Indiana - mostraron que con el número de mediciones no se observan ciertas simetrías específicas. Por lo tanto, demostraron la exactitud de la hipótesis de Zimmer.
Robert Zimmer, ahora presidente de la Universidad de Chicago, desarrolló una hipótesis que lleva su nombre hace casi 40 años.Su trabajo responde a una pregunta importante y larga, abriendo nuevas formas de estudiar muchas otras. También revela las propiedades intrínsecas de los espacios geométricos. La simetría es una de las propiedades más simples de tales espacios. El nuevo trabajo dice que las simetrías pueden existir en espacios de un tipo, y no pueden existir en otros. Este logro se logró después de décadas de inactividad.
"La hipótesis parecía que podría mantener a la gente ocupada durante mucho tiempo", dijo Amy Wilkinson, una matemática de la Universidad de Chicago que organizó la conferencia de este año sobre esta prueba. "Y relativamente simplemente destruyeron esta pregunta".
Simetrías satisfactorias
La simetría es uno de los primeros conceptos geométricos que los niños encuentran en las matemáticas. Con sus propias manos, aprenden que puedes rotar, voltear y cambiar la forma, y al final obtener la misma forma con la que comenzaron. Preservar la forma del objeto como resultado de los cambios responde con una cierta satisfacción interna: esta es una pista de un orden más profundo en el Universo.
Los matemáticos tienen su propio lenguaje formal para estudiar simetría. Les da la oportunidad de discutir en términos concisos sobre varias simetrías que son aplicables en un espacio geométrico dado.
Un cuadrado, por ejemplo, tiene ocho simetrías: ocho formas de voltearlo o rotarlo, obteniendo nuevamente el cuadrado. El círculo se puede girar cualquier cantidad de grados; ella tiene un número infinito de simetrías. Los matemáticos recopilan todas las simetrías de un objeto geométrico o espacio dado, y las agrupan en un "grupo".
Los grupos son interesantes por derecho propio. A menudo aparecen como resultado del estudio de ciertos espacios geométricos, pero a veces aparecen en un contexto que no tiene ninguna relación con la geometría. Por ejemplo, los grupos pueden formar conjuntos numéricos (por ejemplo, hay una cierta simetría al sumar 5 o restar 5 de un número).
"Un grupo, en principio, puede aparecer como una simetría de cosas completamente diferentes", dijo Zimmer.
Hay formas de simetría más exóticas que las que estudiamos en la escuela. Considere, por ejemplo, la simetría de las redes. La red más simple es una cuadrícula bidimensional. En el avión, el enrejado se puede desplazar hacia arriba, hacia abajo, hacia la izquierda, hacia la derecha por cualquier número de cuadrados, y obtener un enrejado que se ve exactamente igual al original. También puede reflejar la cuadrícula a través de cualquier número de celdas individuales. Los espacios con rejillas tienen un número infinito de diferentes simetrías de rejillas.
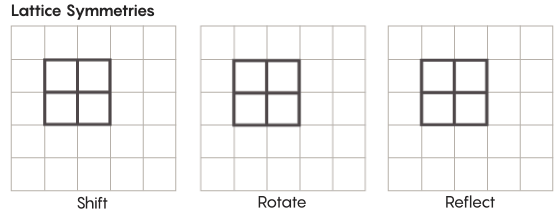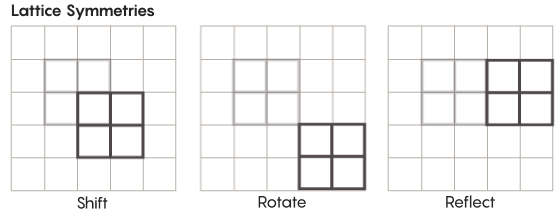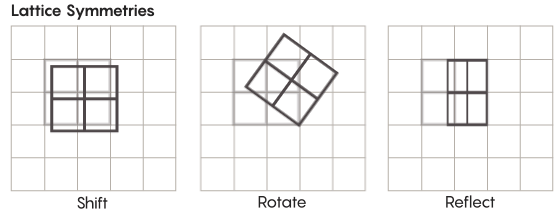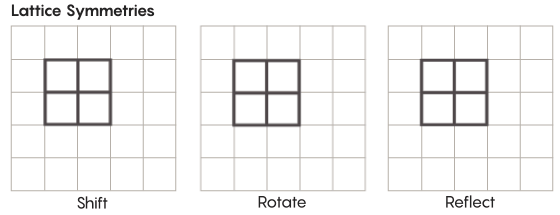
Los enrejados pueden existir en cualquier cantidad de dimensiones. En el espacio tridimensional, una red puede consistir en cubos, no cuadrados. En cuatro o más dimensiones, no será posible presentar la red, pero funciona de la misma manera; los matemáticos pueden describirlo exactamente. Los grupos de interés para la hipótesis de Zimmer incluyen redes de "rango superior", o redes en ciertos espacios de dimensiones superiores. "Esta extraña red sería muy hermosa, si pudiera verse, incluso si no me la hubieran dado", dijo Khurtado-Salazar. "Me parece que mirarla sería muy agradable".
En el siglo XX, los matemáticos descubrieron estos grupos en diversas condiciones, no solo en geometría, sino también en teoría de números, lógica e informática. Al abrir nuevos grupos, es lógico hacer la pregunta: ¿qué tipo de espacios poseen tales conjuntos de simetrías?
A veces, los grupos son obviamente imposibles de igualar espacio. Uno puede entender rápidamente que el grupo de simetrías de un círculo no puede aplicarse a un cuadrado. Gire el cuadrado 10 grados y no obtendrá el cuadrado original. Pero una mezcla de un grupo con un número infinito de simetrías y espacio con muchas dimensiones dificulta la determinación de la aplicabilidad del grupo.
"Al pasar a un grupo más complejo en más dimensiones", dijo Zimmer, "estos problemas se vuelven muy complicados".
Conexión indirecta
Al imaginar la simetría, imaginamos la rotación de toda la forma, por ejemplo, un cuadrado girado 90 grados. Pero en un nivel básico, la simetría depende de los puntos móviles. La transformación simétrica del espacio significa que debe tomar cada punto y moverlo a otro punto. En este sentido, girar el cuadrado 90 grados en realidad significa que debe tomar cada punto del cuadrado y rotarlo 90 grados para que no esté en el borde desde el que comenzó.
David fisherEl problema de los puntos móviles se puede resolver de manera más o menos estricta. Las transformaciones simétricas más familiares (el reflejo de un cuadrado en relación con la diagonal o su rotación en 90 grados) son muy estrictas. Estricto en el sentido de que no mezclan puntos. Los puntos que eran vértices antes de la reflexión siguen siendo vértices después (simplemente se convierten en vértices diferentes), y los puntos que formaban los bordes rectos, después de la reflexión, todavía forman los bordes rectos (simplemente diferentes).
Hay tipos de transformaciones simétricas menos estrictas y más flexibles, y son interesantes en el contexto de la hipótesis de Zimmer. En tales transformaciones, los puntos cambian su organización más fuertemente; no necesariamente retienen sus conexiones anteriores entre sí después de la transformación. Por ejemplo, puede mover cada punto del cuadrado en tres unidades de longitud a lo largo del perímetro del cuadrado; esto satisface los requisitos básicos de una transformación simétrica, es decir, simplemente cambie cada punto en el espacio a otro lugar. Aaron Brown, coautor de la prueba, describió cómo podrían verse estas transformaciones de forma libre en el contexto de la pelota.
“Puedes tomar los polos norte y sur y girarlos en direcciones opuestas. Entonces la distancia entre los puntos aumentará ”, dijo Brown.
En el caso de una cuadrícula, en lugar de simplemente moverla a lo largo del plano, puede doblarla, estirarla en algunos lugares y apretarla en otros, para que la malla transformada ya no se superponga con la original. Dichas transformaciones son menos estrictas y se denominan
difeomorfismos .
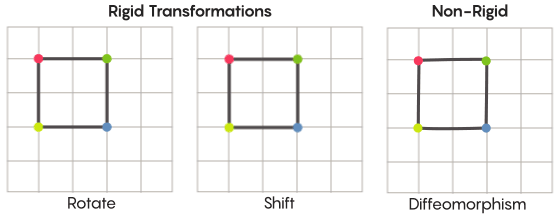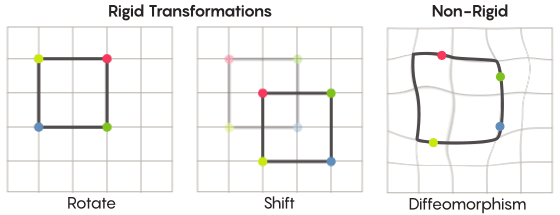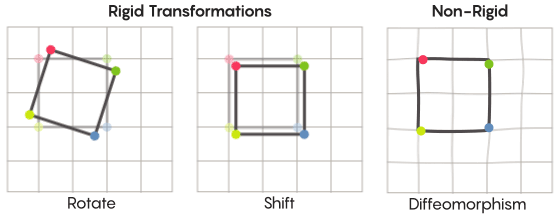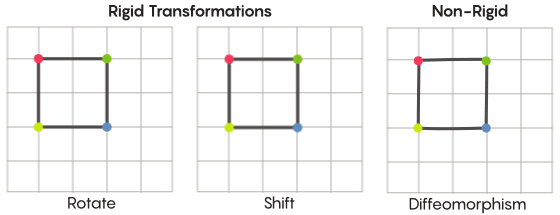
Zimmer tenía buenas razones para usar esta versión menos rigurosa de simetría en su hipótesis.
Grigory Alexandrovich Margulis , quien recibió el
Premio Fields por su trabajo, estudió por primera vez enrejados especiales del rango más alto relacionado con esta hipótesis. Margulis hizo una descripción completa de qué tipo de espacios se pueden transformar utilizando estas redes de rango superior, si solo se permiten transformaciones estrictas.
La hipótesis de Zimmer se convirtió en una continuación natural del trabajo de Margulis. Comienza con una lista de espacios en los que pueden funcionar las redes de alto rango (Margulis descubrió esta lista) y pregunta si esta lista se está expandiendo si se permite que las redes tengan transformaciones menos estrictas.
En el nuevo trabajo, tres matemáticos demostraron que debilitar la definición de simetría no cambia el alcance de las simetrías de las redes de orden superior. Incluso si se permite que las celosías tengan transformaciones muy irregulares - para cambiar, doblar, estirar - las celosías aún tienen una restricción estricta en el alcance.
“Después de agregar tanta flexibilidad al enunciado del problema, intuitivamente, por supuesto, parece que las cuadrículas pueden actuar más ampliamente. Por lo tanto, resulta sorprendente que en realidad la respuesta sea "no", en algunos casos no pueden ", dijo Fisher.
Los matemáticos han establecido correspondencias exactas entre la dimensión del espacio y la dimensión, o rango, de las redes, para redes que pueden desempeñar el papel de simetría en un espacio dado. En general, mostraron que cuanto más alto es el rango de la red, más medidas se necesitan para el espacio que puede acomodarlo. Incluso con una considerable flexibilidad en la transformación del espacio, las transformaciones de redes de alto rango se limitan a dimensiones más altas.
"Esto sugiere que hay algo muy fundamental en la estructura de los espacios, lo que implica su capacidad para acomodar tales transformaciones", dijo Wilkinson.
La hipótesis de Zimmer es solo el primer paso para un programa más amplio. Después de haberlo tratado, los coautores del trabajo impusieron una restricción aproximada de los espacios en los que se pueden transformar las redes de alto rango. La siguiente fase más ambiciosa del trabajo será la concentración en esos espacios en los que pueden existir redes, y luego la clasificación de todas las diferentes formas de transformar las redes de estos espacios.
“Al final, el programa debería poder clasificar todos estos métodos. Hay muchas preguntas interesantes más allá del simple establecimiento del hecho de la existencia de ciertos lugares en los que las rejillas no pueden operar ”, dijo Zimmer.