Julia y retratos de fase de sistemas dinámicos

Continuamos dominando el joven y prometedor lenguaje de propósito general Julia . Pero para empezar, necesitamos exactamente la posibilidad muy limitada de aplicación, para resolver los problemas típicos de la física. Esta es la táctica más conveniente para dominar el instrumento: para obtener una mano, resolveremos problemas apremiantes, aumentando gradualmente la complejidad y encontrando formas de facilitarnos la vida. En resumen, resolveremos diferencias y construiremos gráficos.

Para comenzar, descargue el paquete de gráficos Gadfly e inmediatamente la versión completa del desarrollador, para que funcione bien con nuestra Julia 1.0.1. Conducimos en nuestro cuaderno REPL, JUNO o Jupyter:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master" 

No es la opción más conveniente, pero mientras espera la actualización de PlotlyJS , puede intentarlo en aras de la comparación.

También necesita una herramienta poderosa para resolver ecuaciones diferenciales.

 ]add DifferentialEquations #     

Este es el paquete más extenso y soportado que proporciona muchos métodos para resolver las diferencias. Ahora proceda a los retratos de fase.

Las soluciones de ecuaciones diferenciales ordinarias son a menudo más convenientes para representar en una forma inusual $$$y ^ 1 (t), ..., y ^ L (t)$, y en el espacio de fase a lo largo de los ejes de los cuales se trazan los valores de cada una de las funciones encontradas. Además, el argumento t se incluye en los gráficos solo paramétricamente. En el caso de dos EDO, este gráfico, el retrato de fase del sistema, es una curva en el plano de fase y, por lo tanto, es especialmente evidente.

Oscilador

Dinámica del oscilador armónico $$$\ gamma$se describe mediante el siguiente sistema de ecuaciones:

e independientemente de las condiciones iniciales (x0, y0), llega a un estado de equilibrio, un punto (0,0) con un ángulo de deflexión cero y velocidad cero.

En $$$\ gamma = 0$La solución toma la forma característica de un oscilador clásico.

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end 

Analicemos el código. La función acepta los valores de la frecuencia y el parámetro de atenuación, así como las condiciones iniciales. La función syst () anidada define el sistema. Para que resultara, utilizaron la multiplicación de matrices de una línea. La función solve () , que toma una gran cantidad de parámetros, está configurada de manera muy flexible para resolver el problema, pero solo indicamos el método de solución: Runge-Kutta 4 ( hay muchos otros ), el error relativo y el hecho de que no todos los puntos deben guardarse, sino solo cada cuarto . La matriz de respuesta se almacena en la variable sol , además, sol.t contiene un vector de tiempos, y sol.u resuelve el sistema en estos momentos. Todo esto se dibuja con calma en Plots , y para Gadfly debes completar la respuesta en una matriz más conveniente. No necesitamos tiempos, por lo que solo devolvemos soluciones.

Construyamos un retrato de fase:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2]) 

Entre las funciones de orden superior, broadcast(f, [1, 2, 3]) es especialmente notable para nosotros, que sustituye alternativamente los valores de la matriz [1, 2, 3] en la función f . Breve registro f.([1, 2, 3]) . Esto es útil para variar la frecuencia, el parámetro de atenuación, la coordenada inicial y la velocidad inicial.

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #     

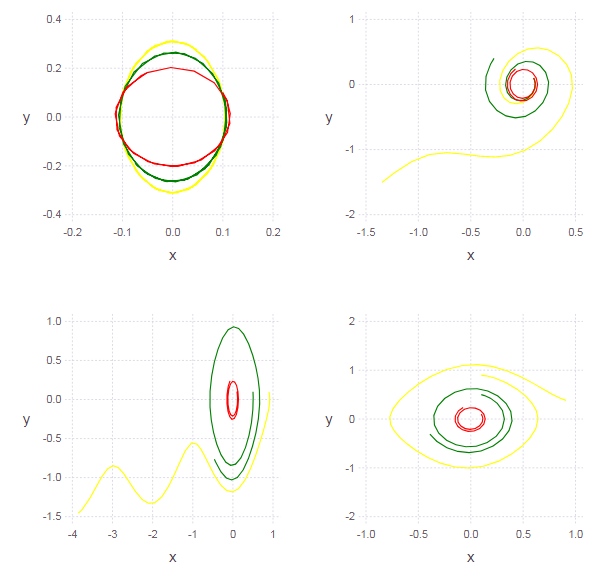
Ahora consideramos no pequeñas oscilaciones, sino oscilaciones de amplitud arbitraria:

El diagrama de fase de la solución no es una elipse (que indica la no linealidad del oscilador). Cuanto menos elijamos la amplitud de las oscilaciones (es decir, las condiciones iniciales), menos linealidad aparecerá (por lo tanto, pequeñas oscilaciones del péndulo pueden considerarse armónicas).

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) ) 

Brusselator

Este modelo describe una cierta reacción química autocatalítica en la que la difusión juega un papel importante. El modelo fue propuesto en 1968 por Lefebvre y Prigozhin.

Funciones desconocidas $$$u_1 (t), \, u_2 (t)$reflejan la dinámica de la concentración de productos intermedios de una reacción química. Parámetro modelo $$$\ mu$La concentración inicial del catalizador (tercera sustancia) tiene sentido.

Con más detalle, la evolución del retrato de fase del brusselator se puede observar realizando cálculos con varios parámetros $$$\ mu$. Con su aumento, el nodo primero cambiará gradualmente a un punto con coordenadas (1, $$$\ mu$) hasta que alcance un valor de bifurcación $$$\ mu$= 2. En este punto, hay una reestructuración cualitativa del retrato, expresada en el nacimiento del ciclo límite. Con mayor aumento $$$\ mu$solo se produce un cambio cuantitativo en los parámetros de este ciclo.

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) 

Suficiente por hoy. La próxima vez, trataremos de aprender a usar otro paquete de gráficos para nuevas tareas, mientras escribimos simultáneamente la sintaxis de Julia. En el proceso de resolución de problemas, lentamente comienza a rastrearse, no es que los pros y los contras sean sencillos ... más bien, las comodidades y los inconvenientes: se debe dedicar una conversación separada a esto. Y, por supuesto, me gustaría ver algo más serio en mi Haber que mis juegos con funciones; por lo tanto, insto a los julistas a que cuenten más sobre proyectos más serios, esto ayudaría a muchos y, en particular, a aprender este maravilloso idioma.