☹️ 🚃 👩🏾‍🤝‍👨🏿 Julia y ecuaciones diferenciales parciales 👍🏾 👩🏻‍🌾 🤦🏼

Usando modelos físicos típicos como ejemplo, consolidaremos las habilidades de trabajar con funciones y nos familiarizaremos con el visualizador PyPlot rápido, conveniente y hermoso, que proporciona todo el poder del Matplotlib Python. Habrá muchas fotos (escondidas debajo de los spoilers)

Nos aseguramos de que todo esté limpio y fresco debajo del capó:

Debajo del capó

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

De lo contrario, obtendremos todo lo que necesitamos para hoy.

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

Ahora a las tareas!

Llevar ecuación

En física, se entiende que el término transferencia significa procesos irreversibles, como resultado de los cuales se produce un movimiento espacial (transferencia) de masa, momento, energía, carga u otra cantidad física en el sistema físico.
La ecuación de transporte unidimensional lineal (o la ecuación de advección), la ecuación diferencial parcial más simple, se escribe como

$\ frac {\ partial U (x, t)} {\ partial t} + c \ frac {\ partial U (x, t)} {\ partial x} = \ Phi (U, x, t)$

Para la solución numérica de la ecuación de transporte, puede usar el esquema de diferencia explícita:

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ Phi_ {i-1} + \ Phi_i} {2}$

donde $\ hat {U}$ - el valor de la función de cuadrícula en la capa de tiempo superior. Este circuito es estable con el número Courant. $K = c \ tau / \ Delta <1$

Transferencia no lineal

$\ frac {\ partial U (x, t)} {\ partial t} + (C_0 + UC_1) \ frac {\ partial U (x, t)} {\ partial x} = \ Phi (U, x, t )$

Fuente de línea (transferencia de absorción): $\ Phi (U, x, t) = - BU$ . Usamos el esquema de diferencia explícita:

$U ^ {j + 1} _i = \ left (1- \ frac {h_tB} {2} - \ frac {h_tC_0} {h_x} - \ frac {h_tC_1} {h_x} U ^ j_i \ right) U ^ j_i + U ^ j_ {i-1} \ left (\ frac {h_tC_0} {h_x} - \ frac {h_tB} {2} + \ frac {h_tC_1} {h_x} U ^ j_i \ right)$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

Resultado

Aumentemos la absorción:

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

Resultado

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

Casi volcado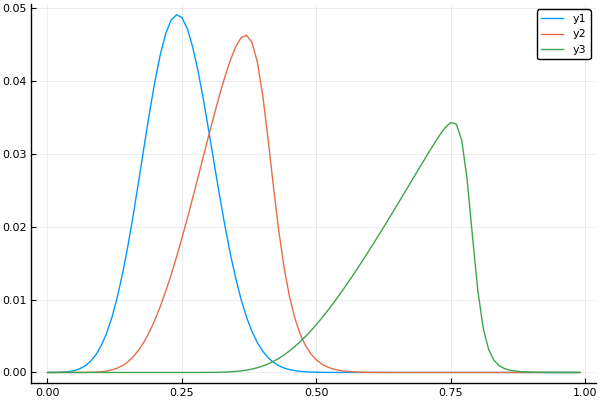

heatmap(t, X, Ans0)

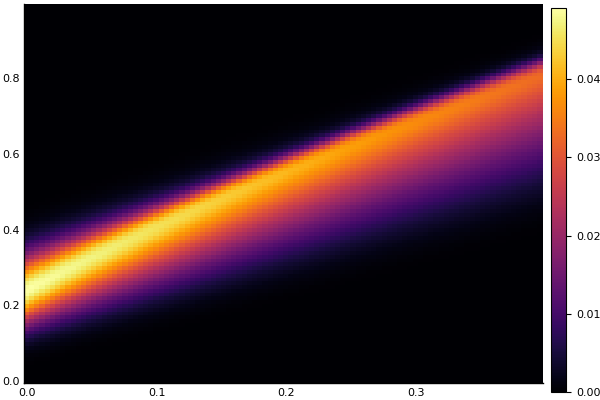
Ecuación de calor

La ecuación diferencial de calor (o la ecuación de difusión de calor) se escribe de la siguiente manera:

$\ frac {\ partial T (x, t)} {\ partial t} + D \ frac {\ partial ^ 2 U (x, t)} {\ partial x ^ 2} = \ phi (T, x, t )$

Esta es una ecuación parabólica que contiene la primera derivada con respecto al tiempo t y la segunda con respecto a la coordenada espacial x. Describe la dinámica de temperatura de, por ejemplo, una varilla metálica de enfriamiento o calentamiento (la función T describe el perfil de temperatura a lo largo de la coordenada x a lo largo de la varilla). El coeficiente D se llama coeficiente de conductividad térmica (difusión). Puede ser constante o depender, tanto explícitamente de las coordenadas como de la función D (t, x, T) deseada.

Considere la ecuación lineal (el coeficiente de difusión y las fuentes de calor son independientes de la temperatura). La aproximación de la diferencia de una ecuación diferencial utilizando los esquemas de Euler explícitos e implícitos, respectivamente:

$\ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ {i-1, n} -2T_ {i, n} + T_ {i + 1 , n}} {\ Delta ^ 2} + \ phi_ {i, n} \\ \ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ { i-1, n + 1} -2T_ {i, n + 1} + T_ {i + 1, n + 1}} {\ Delta ^ 2} + \ phi_ {i, n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

Resultado

Usamos el esquema implícito y el método de barrido.

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

Comparación de circuitos

Ecuación de calor no lineal

Se pueden obtener soluciones mucho más interesantes para la ecuación de calor no lineal, por ejemplo, con una fuente de calor no lineal $\ phi (x, T) = 10 ^ 3 (T-T ^ 3)$ . Si lo configura de esta forma, obtendrá una solución en forma de frentes térmicos, propagándose a ambos lados de la zona de calentamiento primario

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

Frente térmico

Incluso son posibles soluciones más inesperadas con la no linealidad del coeficiente de difusión también. Por ejemplo, si tomas $D (x, T) = T ^ 2$ un $\ phi (x, T) = 10 ^ 3T ^ {3.5}$ , entonces se puede observar el efecto de la combustión del medio, localizado en la región de su calentamiento primario (modo S de combustión "con exacerbación").
Al mismo tiempo, comprobaremos cómo funciona nuestro esquema implícito con la no linealidad de ambas fuentes y el coeficiente de difusión.

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

Modo S

Ecuación de onda

Ecuación de onda hiperbólica

$\ frac {\ partial ^ 2 U (x, t)} {\ partial t ^ 2} = c ^ 2 \ frac {\ partial ^ 2 U (x, t)} {\ partial x ^ 2}$

describe ondas lineales unidimensionales sin dispersión. Por ejemplo, vibraciones de una cuerda, sonido en un líquido (gas) u ondas electromagnéticas en el vacío (en este último caso, la ecuación debe escribirse en forma de vector).

El esquema de diferencia más simple que se aproxima a esta ecuación es un esquema explícito de cinco puntos.

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i + 1} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih, \, t_n = \ tau$

Este esquema, llamado "cruz", tiene un segundo orden de precisión en tiempo y coordenadas espaciales y es de tres capas en el tiempo.

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

Resultado

Para construir una superficie, usaremos PyPlot como un entorno de Plots, pero directamente:

Gráfico de superficie

 using PyPlot surf(t, X, U)

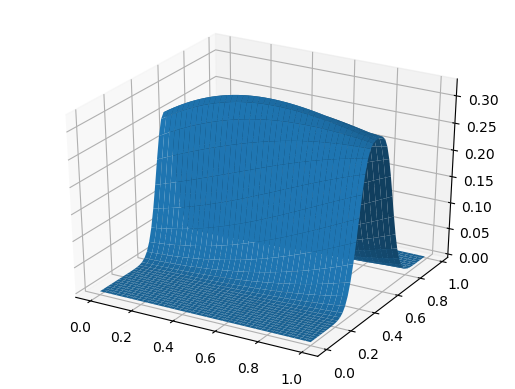
Y para el postre, la ola se propaga a una velocidad que depende de la coordenada:

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

Resultado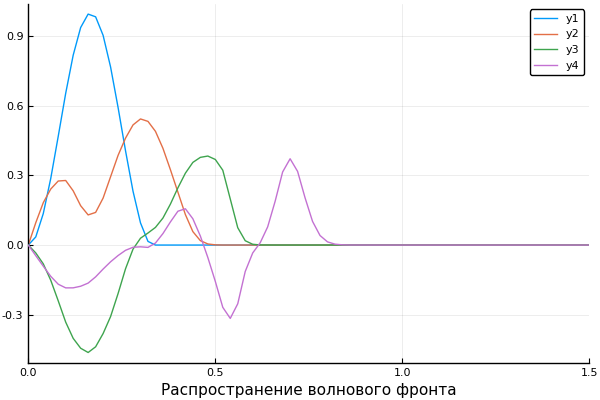

 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

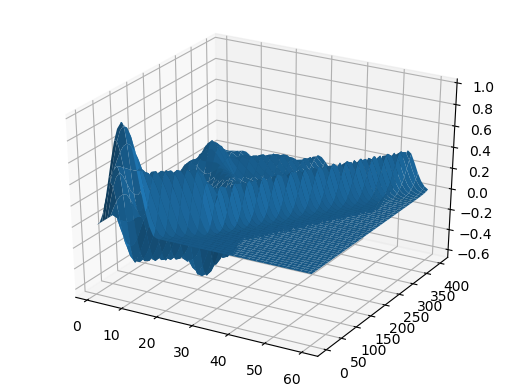
heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

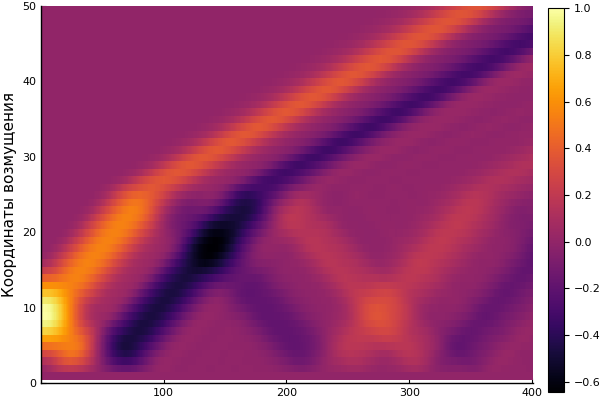
Suficiente por hoy. Para una revisión más detallada:
Enlace de PyPlot a github , otros ejemplos de tramas que se utilizan como entorno y una buena nota en ruso de Julia .

Julia y ecuaciones diferenciales parciales

Llevar ecuación

Transferencia no lineal

Ecuación de calor

Ecuación de calor no lineal

Ecuación de onda

More articles: