Un codificador automático variacional (codificador automático) es un modelo generativo que aprende a mostrar objetos en un espacio oculto dado.

¿Alguna vez se preguntó cómo funciona un modelo variador de codificador automático (VAE)? ¿Quiere saber cómo VAE genera nuevos ejemplos, como el conjunto de datos en el que se formó? Después de leer este artículo, obtendrá una comprensión teórica del funcionamiento interno de VAE, y también puede implementarlo usted mismo. Luego, mostraré el código VAE funcional entrenado en un conjunto de dígitos escritos a mano, y nos divertiremos un poco, ¡generando nuevos dígitos!

Modelos generativos

VAE es un modelo generativo: estima la densidad de probabilidad (PDF) de los datos de entrenamiento. Si dicho modelo está entrenado en imágenes naturales, entonces asignará un valor de alta probabilidad a la imagen del león y un valor bajo a la imagen de mierda al azar.

¡El modelo VAE también sabe cómo tomar ejemplos de PDF capacitados, que es la parte más genial, ya que puede generar nuevos ejemplos similares al conjunto de datos original!

Explicaré VAE usando el conjunto de números manuscritos MNIST . Los datos de entrada para el modelo son imágenes en el formato $$$\ mathbb {R} ^ {28 × 28}$ . El modelo debe evaluar la probabilidad de cuánto se ve la entrada como un dígito.

Tarea de modelado de imagen

La interacción entre píxeles es una tarea difícil. Si los píxeles son independientes entre sí, debe estudiar el PDF de cada píxel de forma independiente, lo cual es fácil. La selección también es simple: tomamos cada píxel por separado.

Pero en las imágenes digitales, existen claras dependencias entre los píxeles. Si ve el comienzo de los cuatro en la mitad izquierda, se sorprenderá mucho si la mitad derecha es la finalización de cero. ¿Pero por qué? ..

Espacio oculto

Sabes que cada imagen tiene un número. Entrada a $$$\ mathbb {R} ^ {28 × 28}$ claramente no contiene esta información. Pero debe estar en algún lugar ... Este "en algún lugar" es un espacio oculto.



Puedes pensar en el espacio oculto como $$$\ mathbb {R} ^ {k}$ donde cada vector contiene $$$k$ piezas de información necesarias para representar una imagen. Supongamos que la primera dimensión contiene un número representado por un dígito. La segunda dimensión puede ser el ancho. El tercero es el ángulo, y así sucesivamente.

Podemos imaginar el proceso de dibujar a una persona en dos pasos. Primero, una persona determina, conscientemente o no, todos los atributos del número que se mostrará. A continuación, estas decisiones se transforman en trazos sobre papel.

VAE está tratando de simular este proceso: para una imagen determinada $$$x$ queremos encontrar al menos un vector oculto que pueda describirlo; un vector que contiene instrucciones para generar $$$x$ . Formulando la fórmula de probabilidad total , obtenemos $$$P (x) = \ int P (x | z) P (z) dz$ .

Pongamos un sentido razonable en esta ecuación:

• Integral significa que los candidatos deben buscarse en todo el espacio oculto.
• Para cada candidato $$$z$ hacemos la pregunta: ¿es posible generar $$$x$ usando instrucciones $$$z$ ? ¿Es lo suficientemente grande? $$$P (x | z)$ ? Por ejemplo, si $$$z$ codifica información sobre el dígito 7, entonces la imagen 8 no es posible. Sin embargo, la imagen 1 es aceptable porque 1 y 7 son similares.
• Encontramos uno bueno. $$$z$ ? Genial Pero espera un segundo ... cuánto cuesta $$$z$ probablemente? $$$P (z)$ lo suficientemente grande? Considere la imagen del número invertido 7. Una coincidencia ideal sería un vector oculto que describe la vista 7, donde el tamaño del ángulo se establece en 180 °. Sin embargo tal $$$z$ Es poco probable, porque generalmente los números no se escriben en un ángulo de 180 °.

El objetivo del entrenamiento VAE es maximizar $$$P (x)$ . Vamos a modelar $$$P (x | z)$ utilizando distribución gaussiana multidimensional $$$\ mathcal {N} (f (z), \ sigma ^ 2 \ cdot I)$ .

$$$f (z)$ modelado utilizando una red neuronal. $$$\ sigma$ Es un hiperparámetro para multiplicar la matriz de identidad. $$$I$ .

Ten en cuenta que $$$f$ - esto es lo que usaremos para generar nuevas imágenes usando un modelo entrenado. La superposición de una distribución gaussiana es solo para fines educativos. Si tomamos la función delta de Dirac (es decir, determinista $$$x = f (z)$ ), ¡entonces no podremos entrenar el modelo usando el descenso en gradiente!

Las maravillas del espacio oculto.

El enfoque del espacio oculto tiene dos grandes problemas:

1. ¿Qué información contiene cada dimensión? Algunas dimensiones pueden relacionarse con elementos abstractos, como el estilo. Incluso si fuera fácil interpretar todas las dimensiones, no queremos asignar etiquetas al conjunto de datos. Este enfoque no escala a otros conjuntos de datos.
2. El espacio oculto puede confundirse cuando existe una correlación entre las dimensiones. Por ejemplo, un número dibujado muy rápidamente puede conducir simultáneamente a la aparición de trazos angulares y más delgados. Definir estas dependencias es difícil.

El aprendizaje profundo viene al rescate

Resulta que cada distribución se puede generar aplicando una función bastante compleja a la distribución gaussiana multidimensional estándar.

Elegir $$$P (z)$ como una distribución gaussiana multidimensional estándar. Así modelado por una red neuronal $$$f$ se puede dividir en dos fases:

1. Las primeras capas mapean la distribución gaussiana en la distribución verdadera sobre el espacio oculto. No podemos interpretar las medidas, pero no importa.
2. Las capas posteriores se mostrarán desde el espacio oculto en $$$P (x | z)$ .

Entonces, ¿cómo entrenamos a esta bestia?

Fórmula para $$$P (x)$ insoluble, por lo tanto, lo aproximamos por el método de Monte Carlo:

1. Selección $$$\ {z_i \} _ {i = 1} ^ n$ del anterior $$$P (z)$
2. Aproximación con $$$P (x) \ aprox \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

Genial Así que prueba muchas cosas diferentes $$$z$ y comienza la fiesta de propagación de errores!

Lamentablemente desde $$$x$ muy multidimensional, para obtener una aproximación razonable, se requieren muchas muestras. Quiero decir si lo intentas $$$z$ , ¿cuáles son las posibilidades de obtener una imagen que se parece a $$$x$ ? Esto, por cierto, explica por qué $$$P (x | z)$ debe asignar un valor de probabilidad positivo a cualquier imagen posible, de lo contrario el modelo no podrá aprender: muestreo $$$z$ dará como resultado una imagen que seguramente es diferente de $$$x$ , y si la probabilidad es 0, entonces los gradientes no podrán propagarse.

¿Cómo resolver este problema?

¡Corta el camino!

La mayoría de las muestras $$$z$ no se agregará nada de la selección a $$$P (x)$ - Están demasiado lejos de sus fronteras. Ahora, si supieras de antemano de dónde sacarlos ...

Puede entrar $$$Q (z | x)$ . Dado $$$Q$ será entrenado para asignar valores de alta probabilidad a $$$z$ que es probable que generen $$$x$ . Ahora puede hacer una evaluación utilizando el método Monte Carlo, tomando muchas menos muestras de $$$Q$ .

¡Desafortunadamente, surge un nuevo problema! En lugar de maximizar $$$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$ maximizamos $$$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$ . ¿Cómo se relacionan entre sí?

Conclusión variacional

La conclusión variacional es el tema de un artículo separado, por lo que no me detendré aquí en detalle. Solo puedo decir que estas distribuciones están relacionadas por esta ecuación:

$$

$$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [log P (x | z)] - \ mathcal {KL} [Q (z | x) || P (z)]$$

$$$\ mathcal {KL}$ es la distancia Kullback - Leibler , que evalúa intuitivamente la similitud de las dos distribuciones.

En un momento, verá cómo maximizar el lado derecho de la ecuación. En este caso, el lado izquierdo también se maximiza:

• $$$P (x)$ maximizado
• que tan lejos $$$Q (z | x)$ de $$$P (z | x)$ - real a priori desconocido - se minimizará.

El significado del lado derecho de la ecuación es que tenemos tensión aquí:

1. Por un lado, queremos maximizar qué tan bien $$$x$ debe ser decodificado desde $$$z \ sim Q$ .
2. Por otro lado, queremos $$$Q (z | x)$ ( codificador ) fue similar al anterior $$$P (z)$ (distribución gaussiana multidimensional). Esto puede verse como regularización.

Minimización de la divergencia. $$$\ mathcal {KL}$ realizado fácilmente con la correcta selección de distribuciones. Simularemos $$$Q (z | x)$ como una red neuronal, cuyo resultado son los parámetros de una distribución gaussiana multidimensional:

• promedio $$$\ mu_Q$
• matriz de covarianza diagonal $$$\ Sigma_Q$

Entonces divergencia $$$\ mathcal {KL}$ se vuelve analíticamente solucionable, lo cual es excelente para nosotros (y para los gradientes).

La parte del decodificador es un poco más complicada. A primera vista, me gustaría decir que este problema no se puede resolver con el método de Monte Carlo. Pero la muestra $$$z$ de $$$Q$ no permitirá que los gradientes se propaguen a través de $$$Q$ , porque la selección no es una operación diferenciable. Esto es un problema, ya que los pesos de las capas que emiten $$$\ Sigma_Q$ y $$$\ mu_Q$ .

Nuevo truco de parametrización

Podemos reemplazar $$$Q$ transformación parametrizada determinista de una variable aleatoria no paramétrica:

1. Una muestra de la distribución gaussiana estándar (sin parámetros).
2. Multiplicar la muestra por la raíz cuadrada $$$\ Sigma_Q$ .
3. Agregando al resultado $$$\ mu_Q$ .

Como resultado, obtenemos una distribución igual a $$$Q$ . Ahora la operación de recuperación proviene de la distribución gaussiana estándar. En consecuencia, los gradientes pueden propagarse a través de $$$\ Sigma_Q$ y $$$\ mu_Q$ desde ahora estos son caminos deterministas.

Resultado? El modelo podrá aprender a ajustar los parámetros. $$$Q$ : ella se concentrará en lo bueno $$$z$ que son capaces de producir $$$x$ .

Poniendo todo junto

El modelo VAE puede ser difícil de entender. Hemos examinado aquí mucho material que es difícil de digerir.

Permítanme resumir todos los pasos para implementar VAE.



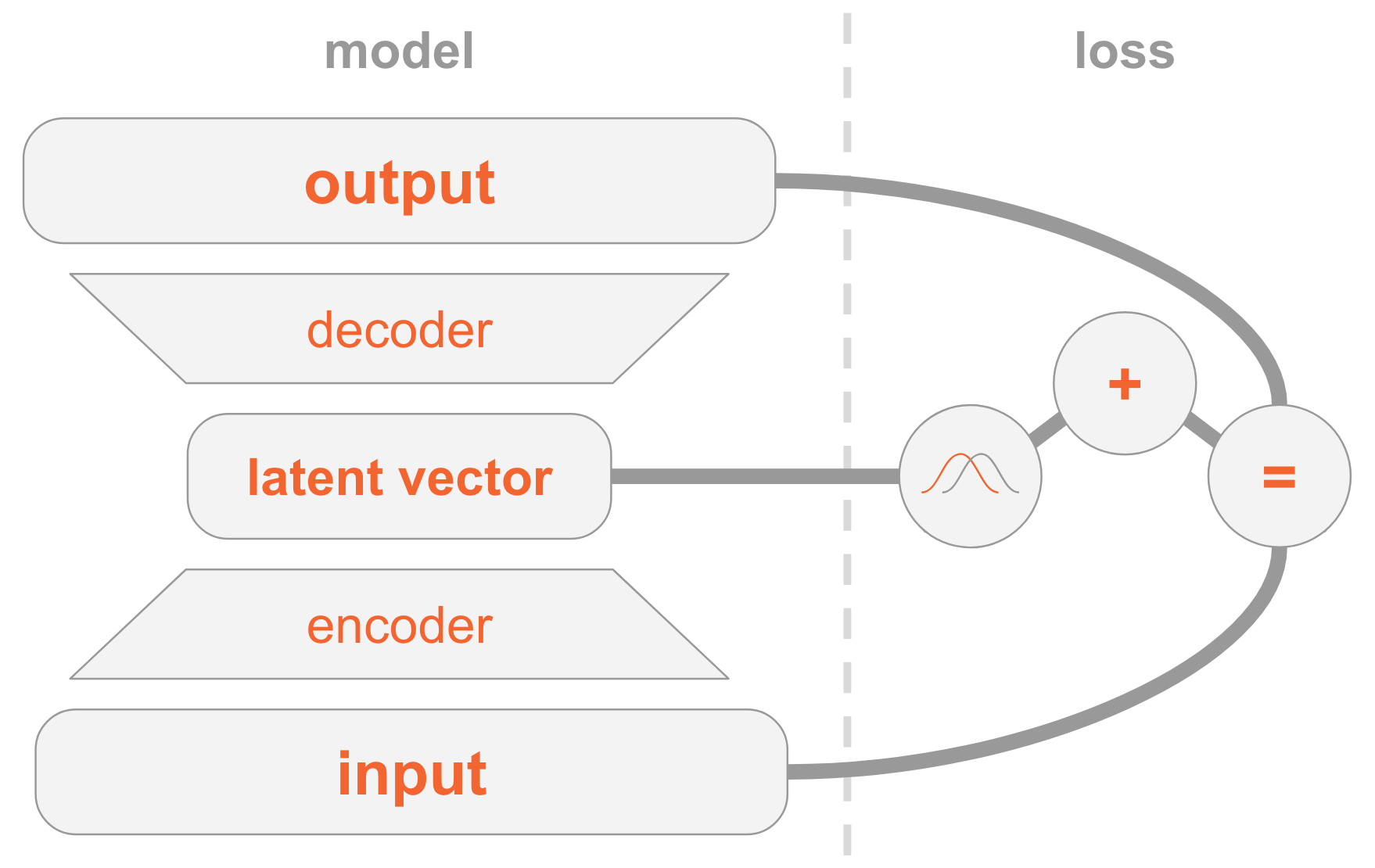
A la izquierda tenemos una definición de modelo:

1. La imagen de entrada se transmite a través de la red del codificador.
2. El codificador proporciona parámetros de distribución. $$$Q (z | x)$ .
3. Vector oculto $$$z$ tomado de $$$Q (z | x)$ . Si el codificador está bien entrenado, en la mayoría de los casos $$$z$ contener una descripción $$$x$ .
4. Decodificador decodifica $$$z$ en la imagen

En el lado derecho, tenemos una función de pérdida:

1. Error de recuperación: la salida debe ser similar a la entrada.
2. $$$Q (z | x)$ debería ser similar a la anterior, es decir, una distribución normal estándar multidimensional.

Para crear nuevas imágenes, puede seleccionar directamente el vector oculto de la distribución anterior y decodificarlo en una imagen.

Código de trabajo

Ahora estudiaremos VAE con más detalle y consideraremos el código de trabajo. Comprenderá todos los detalles técnicos necesarios para implementar VAE. Como beneficio adicional, mostraré un truco interesante: cómo asignar roles especiales a algunas dimensiones del vector oculto para que el modelo comience a generar imágenes de los números indicados.

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

Les recuerdo que las modelos están entrenadas en MNIST , un conjunto de números escritos a mano. Las imágenes de entrada vienen en el formato $$$\ mathbb {R} ^ {28 × 28}$ .

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

A continuación, definimos hiperparámetros.

Siéntase libre de jugar con diferentes valores para tener una idea de cómo afectan al modelo.

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

Modelo

El modelo consta de tres subredes:

1. Consigue $$$x$ (imagen), lo codifica en una distribución $$$Q (z | x)$ en espacio escondido
2. Consigue $$$z$ en un espacio oculto (representación de código de la imagen), la decodifica en la imagen correspondiente $$$f (z)$ .
3. Consigue $$$x$ y determina el número en comparación con la capa de 10 dimensiones, donde el valor i-ésimo contiene la probabilidad del número i-ésimo.

Las dos primeras subredes son la base de VAE puro.

La tercera es una tarea auxiliar que utiliza algunas de las dimensiones ocultas para codificar los números encontrados en la imagen. Explicaré por qué: anteriormente discutimos que no nos importa qué información contiene cada dimensión del espacio oculto. Un modelo puede aprender a codificar cualquier información que considere valiosa para su tarea. Como estamos familiarizados con el conjunto de datos, sabemos la importancia de la dimensión, que contiene el tipo de dígito (es decir, su valor numérico). Y ahora queremos ayudar a la modelo brindándole esta información.

Para un tipo de dígito dado, lo codificamos directamente, es decir, usamos un vector de tamaño 10. Estos diez números están asociados con un vector oculto, por lo que al decodificar este vector en una imagen, el modelo usará información digital.

Hay dos formas de proporcionar modelos de vector de codificación directa:

1. Agréguelo como entrada al modelo.
2. Agréguelo como una etiqueta, para que el modelo mismo calcule el pronóstico: agregaremos otra subred que predice un vector de 10 dimensiones, donde la función de pérdida es la entropía cruzada con el vector de codificación directo esperado.

Elige la segunda opción. Por qué Bueno, entonces, al probar, puede usar el modelo de dos maneras:

1. Especifique la imagen como entrada y muestre un vector oculto.
2. Especifique un vector oculto como entrada y genere una imagen.

Como queremos admitir la primera opción, no podemos darle al modelo un dígito como entrada, porque no queremos saberlo durante las pruebas. Por lo tanto, el modelo debe aprender a predecirlo.

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

Entrenamiento

Entrenaremos un modelo para optimizar dos funciones de pérdida - VAE y clasificación - usando SGD .

Al final de cada época, seleccionamos vectores ocultos y los decodificamos en imágenes para observar visualmente cómo mejora el poder generativo del modelo durante las épocas. El método de muestreo es el siguiente:

1. Establezca explícitamente las dimensiones que se utilizan para clasificar por el dígito que queremos generar. Por ejemplo, si queremos crear una imagen del número 2, entonces establecemos las medidas $$$[0010000000]$ .
2. Seleccione al azar de otras dimensiones de la distribución normal multidimensional. Estos son los valores para los diferentes números que se generan en esta era. Entonces tenemos una idea de lo que está codificado en otras dimensiones, por ejemplo, el estilo de escritura a mano.

El significado del paso 1 es que después de la convergencia, el modelo debería poder clasificar la figura en la imagen de entrada por estos ajustes de medición. Sin embargo, también se usan en la fase de decodificación para crear una imagen. Es decir, la subred del decodificador sabe: cuando las medidas corresponden al número 2, debe generar una imagen con este número. Por lo tanto, si establecemos manualmente las medidas en el número 2, obtendremos una imagen generada de esta figura.

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

Verifiquemos que ambas funciones de pérdida se vean bien, es decir, disminuyan:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

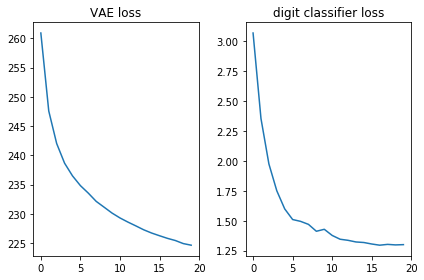
Además, visualicemos las imágenes generadas y veamos si el modelo realmente puede crear imágenes con números escritos a mano:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

Conclusión

Es agradable ver que una red de distribución directa simple (sin convoluciones elegantes) genera bellas imágenes en solo 20 eras. El modelo aprendió rápidamente a usar medidas especiales para los números: en la novena era, ya vemos la secuencia de números que estábamos tratando de generar.

Cada época usaba diferentes valores aleatorios para otras dimensiones, por lo que el estilo es diferente entre las épocas, pero es similar dentro de ellas: al menos dentro de algunas. Por ejemplo, en el 18, todos los números son más gordos en comparación con el 20.

Notas

El artículo se basa en mi experiencia y las siguientes fuentes:

• Conclusión variacional y aprendizaje profundo: una nueva síntesis
• Guía de variación del codificador automático