Curso MIT "Seguridad de sistemas informáticos". Lección 16: "Ataques de canal lateral", Parte 1

Instituto de Tecnología de Massachusetts. Conferencia Curso # 6.858. "Seguridad de los sistemas informáticos". Nikolai Zeldovich, James Mickens. Año 2014

Computer Systems Security es un curso sobre el desarrollo e implementación de sistemas informáticos seguros. Las conferencias cubren modelos de amenazas, ataques que comprometen la seguridad y técnicas de seguridad basadas en trabajos científicos recientes. Los temas incluyen seguridad del sistema operativo (SO), características, gestión del flujo de información, seguridad del idioma, protocolos de red, seguridad de hardware y seguridad de aplicaciones web.

Lección 1: "Introducción: modelos de amenaza" Parte 1 / Parte 2 / Parte 3
Lección 2: "Control de ataques de hackers" Parte 1 / Parte 2 / Parte 3
Lección 3: “Desbordamientos del búfer: exploits y protección” Parte 1 / Parte 2 / Parte 3
Lección 4: “Separación de privilegios” Parte 1 / Parte 2 / Parte 3
Lección 5: “¿De dónde vienen los sistemas de seguridad?” Parte 1 / Parte 2
Lección 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Lección 7: “Sandbox de cliente nativo” Parte 1 / Parte 2 / Parte 3
Lección 8: "Modelo de seguridad de red" Parte 1 / Parte 2 / Parte 3
Lección 9: "Seguridad de aplicaciones web" Parte 1 / Parte 2 / Parte 3
Lección 10: “Ejecución simbólica” Parte 1 / Parte 2 / Parte 3
Lección 11: "Ur / Lenguaje de programación web" Parte 1 / Parte 2 / Parte 3
Lección 12: Seguridad de red Parte 1 / Parte 2 / Parte 3
Lección 13: "Protocolos de red" Parte 1 / Parte 2 / Parte 3
Lección 14: "SSL y HTTPS" Parte 1 / Parte 2 / Parte 3
Lección 15: "Software médico" Parte 1 / Parte 2 / Parte 3
Lección 16: "Ataques de canal lateral" Parte 1 / Parte 2 / Parte 3

Ok chicos, comencemos. Entonces, hoy hablaremos sobre los ataques a través de canales secundarios, un problema común inherente a todo tipo de sistemas. En un sentido amplio, los ataques a través del canal lateral ocurren en una situación en la que no cree que alguna información sea capaz de revelar información sobre su sistema.



Por lo general, tiene varios componentes que establecen una conexión entre el usuario y el servidor. Al mismo tiempo, cree que sabe todo lo que pasa a través de este cable que conecta a dos suscriptores, sabe todos los bits que el usuario y el servidor intercambian entre sí, y esto es seguro. Pero a menudo sucede que parte de la información aún es revelada por el usuario o el servidor. El ejemplo descrito en la conferencia de hoy describe una situación en la que la sincronización de mensajes entre el usuario y el servidor revela información adicional que no conocería, simplemente observando el flujo de bits entre estos suscriptores.

De hecho, hay una clase mucho más amplia de canales laterales de los que puede preocuparse. La gente se enteró de la aparición de canales laterales en los años 40, cuando descubrieron que si comienzas a escribir caracteres en un teletipo, la electrónica del teletipo comenzará a emitir radiación de radiofrecuencia. En este caso, simplemente puede colocar el osciloscopio junto a él y observar cómo cambia la frecuencia de la señal de radio según el símbolo que imprima el operador de teletipo. Por lo tanto, la radiación RF es un ejemplo clásico de un canal lateral que te preocupa.

Hay muchos otros ejemplos notados por las personas, como el consumo de electricidad. Este es otro canal lateral del que puede preocuparse, ya que su computadora usará una cantidad diferente de energía dependiendo de lo que calcule.



Un ejemplo de un canal lateral es el sonido, debido a que también es posible la fuga de información. Por ejemplo, las personas escuchan la impresora y, según los sonidos que emiten, pueden decir qué caracteres imprime. Esto es especialmente fácil para las impresoras matriciales que producen sonidos muy molestos durante la impresión.

En general, esto es algo en lo que pensar. En una conferencia del lunes, Kevin también mencionó algunos canales secundarios interesantes con los que trata en su investigación. Pero vamos a ver el canal lateral específico que estudiaron David Bramley y Dan Bone. En su trabajo, publicado hace unos 10 años, escriben que pudieron extraer la clave criptográfica del servidor web Apache midiendo el tiempo de diferentes respuestas a varios paquetes de entrada de un cliente hostil. En este caso particular, "buscaron" una clave criptográfica. De hecho, muchos ataques a través del canal lateral apuntan a claves criptográficas en parte porque es bastante difícil obtener una gran cantidad de datos a través de dicho canal. Y las claves criptográficas son una de las situaciones en las que se emite un pequeño número de bits, es decir, durante un ataque, los atacantes pueden extraer alrededor de 200 a 256 bits de información. Pero basándose solo en estos 200 bits, pueden descifrar la clave criptográfica de este servidor web.

Si está tratando de ingresar a algún tipo de base de datos llena de números de seguridad social, deberá "fusionar" una gran cantidad de información. Es por eso que la mayoría de los ataques de canal lateral se centran en obtener pequeños secretos como claves criptográficas o contraseñas. Pero en general, esto se aplica a muchas otras situaciones.

En los materiales de la conferencia se describe otra cosa interesante: esto es que todo esto se puede hacer a través de la red. Probablemente se dio cuenta de que tenían que hacer mucho trabajo cuidadoso para captar estas pequeñas diferencias en la información de tiempo. Cada solicitud que enviaron al servidor difería de otra solicitud en 1-2 microsegundos, que es un período de tiempo muy corto. Por lo tanto, debe tener mucho cuidado, porque nuestras redes no nos permiten detectar una diferencia tan temporal y determinar que el servidor ha procesado su solicitud durante 1-2 microsegundos más de lo debido.



Como resultado, no estaba claro si tal ataque podría organizarse en una red muy "ruidosa", ya que la información útil debería separarse del nivel de ruido. Estos tipos estuvieron entre los primeros en demostrar que realmente se puede hacer esto a través de una red Ethernet con un servidor en un extremo de la red y un cliente en el otro extremo. Probaron que de hecho es posible medir estas diferencias en parte promediando, en parte con otros trucos.
El plan para el resto de esta conferencia es el siguiente: primero profundizamos en los detalles del algoritmo criptográfico de clave pública RSA que usaron estos tipos. No lo evaluaremos desde el punto de vista de la seguridad, pero veremos cómo se implementa, porque es la implementación del algoritmo lo que es crítico para usar el canal lateral.

Bramley y Bone examinaron los diversos detalles de implementación para comprender cuándo ciertas cosas se desempeñaron más rápido o más lento. Entonces, primero debemos averiguar cómo se implementa el criptosistema RSA, y luego volveremos y descubriremos cómo atacar todas estas estructuras disponibles en RSA.

Comencemos revisando el RSA a un alto nivel. RSA es un criptosistema de clave pública bastante utilizado. Mencionamos a estos tipos hace un par de semanas cuando hablamos de certificados. Ahora vamos a ver cómo funciona realmente.

Como regla general, debe preocuparse por 3 cosas: la generación, el cifrado y el descifrado de claves. En RSA, la forma de crear una clave es seleccionar 2 enteros primos grandes, denotándolos con py q. En su artículo, estos tipos escriben sobre pyq cada uno con un tamaño de 512 bits. Esto generalmente se llama un RSA de 1024 bits, porque el producto de estos primos es un entero de 1000 bits. En estos días, probablemente esta no sea una buena opción para el tamaño de la clave RSA, porque romperla es una tarea relativamente fácil para los atacantes. Entonces, si hace 10 años, 1000 bits parecían una cantidad razonable, hoy, al construir un sistema, debe elegir una clave RSA de 2000, 3000 o incluso 4000 bits. Entonces, el tamaño de la clave RSA significa el tamaño de estos números primos.

Luego, por conveniencia, hablaremos sobre el número n, que es simplemente el producto de estos números primos n = pq, y este número se llama módulo. Entonces, ahora que sabemos cómo crear la clave, o al menos parte de la clave, tendremos que descubrir cómo cifrar y descifrar mensajes.



Y la forma en que encriptaremos y desencriptaremos los mensajes se basa en elevar a la potencia de los números el módulo n. Parece un poco extraño, pero lo resolveremos en un segundo. Entonces, si desea cifrar el mensaje m, debe convertirlo a m ^e con mod n. El valor de e es un grado, en un segundo descubriremos cómo elegirlo. Así es como vamos a encriptar el mensaje.

Es decir, simplemente tomamos este mensaje como un número entero y lo elevamos a un poder. En un segundo veremos por qué funciona esto, pero por ahora, denotaremos todo este mensaje cifrado con la letra C.

Luego, para descifrarlo, debemos encontrar otro exponente interesante d, que nos permita tomar el mensaje cifrado C, elevarlo al módulo d de potencia y, como resultado, obtener mágicamente el mensaje descifrado m.

Entonces, el principio general es usar un exponente para cifrar un mensaje y otro exponente para descifrarlo.



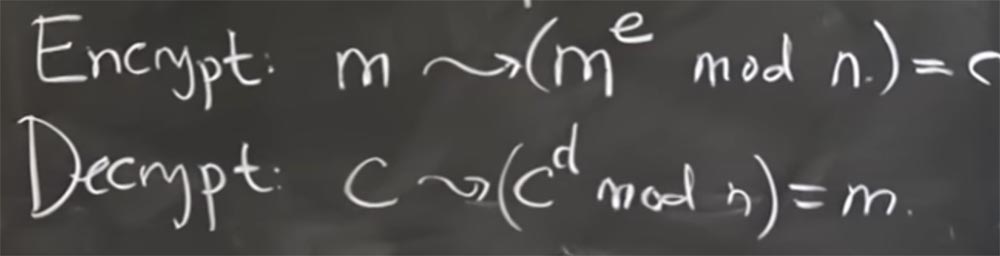
Con todo, parece un poco difícil entender cómo vamos a llegar a estos dos números mágicos que de alguna manera nos devuelven el mensaje original. Pero si observa cómo funciona el módulo de exponenciación o multiplicación de este número n, comprenderá todo.

Si tomamos X y lo elevamos a la potencia igual a la función φ de n, entonces será 1 módulo n:

X ^{φ (n)} = 1 mod n

Esta función phi para nuestra elección particular de n es bastante simple; es igual a φ = (p-1) (q-1).
Entonces el producto del exponente abierto e, que es mayor que 1 pero menor que φ (n), por el exponente secreto d, será igual a:

ed = ɑφ (n) +1, donde ɑ es una constante.

Por lo tanto, es posible descifrar correctamente el mensaje, ya que existe un algoritmo bastante simple si conoce el valor de φ (n) para calcular d teniendo en cuenta e o e teniendo en cuenta d.

Público: ¿1 módulo n no es igual a 1?

Profesor: sí, cometí un error aquí, la igualdad debería verse así:

X ^{φ (n)} _{mod n} = 1 mod n, es decir, el valor de X en el grado de la función "fi" de n módulo n es igual a la unidad módulo n.

Esto básicamente significa que para RSA tenemos que elegir algún valor e, que será nuestro valor de cifrado. Luego, desde e vamos a generar d en base a la fórmula de = 1 mod φ (n), por lo tanto, d = 1 / e mod φ (n).



Existen algunos algoritmos euclidianos que puede usar de manera efectiva para este cálculo. Pero para hacer esto, debe saber esto φ (n), que requiere factorización, es decir, la factorización de nuestro número n en los factores py q.

Entonces, RSA es un sistema donde la clave pública es un par: el exponente de cifrado e y el número n, y el par d y n es una clave privada que se mantiene en secreto. Para que cualquiera pueda aumentar el poder de cifrarlo por usted. Pero solo usted conoce este valor de d y, por lo tanto, puede descifrar el mensaje. Y hasta que sepa la factorización de estos factores P y Q, o N, igual al producto de P y Q, no sabrá qué es φ = (p-1) (q-1).



Como resultado, calcular este valor de d es una tarea bastante difícil. De esto se trata el algoritmo RSA de alto nivel.

Ahora que nos hemos familiarizado con los principios de RSA, quiero detenerme en 2 cosas. Hay trucos sobre cómo usarlo correctamente y hay dificultades que surgen al usarlo. Hay muchas formas de implementar código para esta exponenciación y hacerlo de manera eficiente. Esta es una tarea bastante extraordinaria, porque estamos tratando con enteros de 1000 bits, para los cuales no puede simplemente ejecutar la instrucción de multiplicación. Probablemente llevará mucho tiempo completar estas operaciones.

Por lo tanto, lo primero que quiero mencionar son las diversas trampas de RSA. Uno de ellos es la multiplicación. Supongamos que tenemos 2 mensajes: m ₀ ym ₁ . Los cifraré, convirtiendo m ₀ en m ₀ ^e mod n, y m1 en m ₁ ^e mod n. Un posible problema, o más bien, no necesariamente un problema, pero una sorpresa desagradable para alguien que usa RSA es que es muy fácil encriptar el producto m ₀ por m ₁ , porque simplemente multiplica estos 2 dígitos: m ₀ ^e mod n * m ₁ ^e mod n.



Si los multiplica, terminará con el producto (m ₀ m ₁ ) ^e módulo n. Este es el cifrado correcto con el uso simplificado de RSA para el valor m ₀ m ₁ . Este no es un gran problema en este momento, porque simplemente puede crear este mensaje cifrado, pero no puede descifrarlo. Sin embargo, es posible que un sistema común le permita descifrar mensajes específicos. Es decir, si le permite descifrar el mensaje que creó, entonces quizás siguiendo la ruta inversa, puede descubrir cuáles son estos mensajes m ₀ ym ₁ .

Este hecho no debe ignorarse, ya que afecta a varios protocolos que utilizan RSA. Hay una propiedad que usaremos como mecanismo de defensa al final de nuestra conferencia.

La segunda trampa, o propiedad de RSA, a la que debe prestar atención es el determinismo o determinabilidad. En la implementación primaria descrita anteriormente, si toma el mensaje my lo encripta, convirtiéndolo en m ^e mod n, entonces esta es una función de mensaje determinista. Por lo tanto, si lo vuelve a cifrar, obtendrá exactamente el mismo cifrado.

Esta no es una propiedad deseable, porque si veo que está enviando un mensaje cifrado con RSA y quiero saber de qué se trata, puede ser difícil para mí descifrarlo. Pero puedo probar cosas diferentes, como resultado de lo cual veo que estás enviando este mensaje.

Luego lo cifraré y veré si obtiene el mismo texto cifrado. Y si es así, descubriré que has encriptado. Porque todo lo que necesito para cifrar un mensaje es una clave pública de acceso público, que es un par de números (n, e).

Por lo tanto, esto no es tan bueno, y es posible que tenga que tener cuidado con esta propiedad al usar RSA. Por lo tanto, las primitivas de este tipo son difíciles de usar directamente.



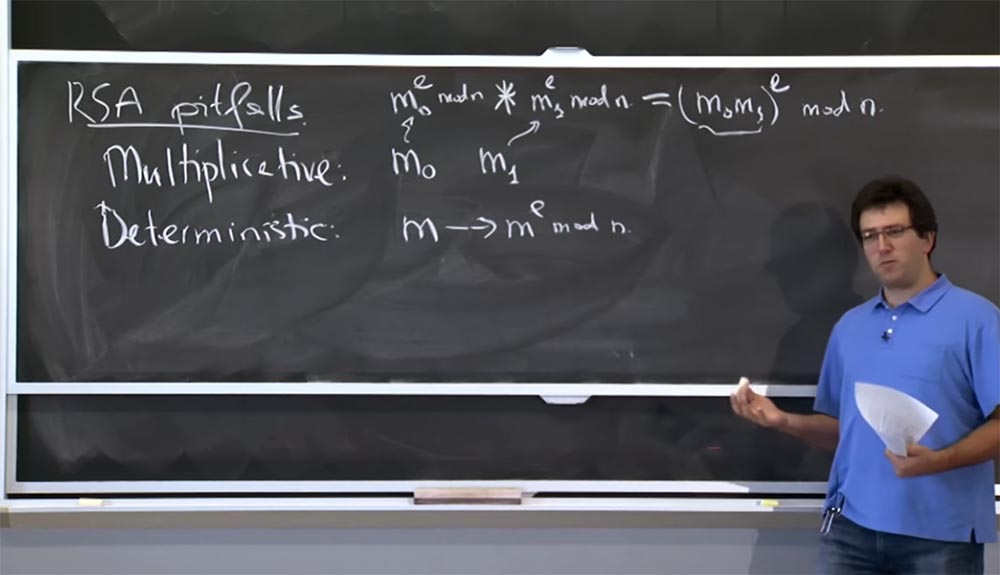
En la práctica, para evitar problemas similares con RSA, las personas codifican el mensaje de cierta manera antes del cifrado. En lugar de elevar directamente un mensaje a una potencia, toman algún tipo de función de mensaje y lo elevan a un módulo de potencia n:

(f (m)) ^e mod n.

Esta función f, comúnmente utilizada hoy en día, se llama OAEP: cifrado asimétrico óptimo con adición. Esto es algo codificado con dos propiedades interesantes.

En primer lugar, trae aleatoriedad. Puede pensar que f (m) genera un mensaje de 1000 bits que va a cifrar. Parte de este mensaje será tu mensaje aquí en el medio de este rectángulo. Por supuesto, puede recuperarlo cuando descifre. Entonces, hay 2 cosas interesantes que quieres hacer: a la derecha colocas algún tipo de aleatoriedad, el valor de r. Esto da que si encriptas un mensaje varias veces, obtendrás resultados diferentes cada vez, por lo que el cifrado ya no se determinará.

Para superar esta propiedad multiplicativa y otros tipos de problemas, a la izquierda tiene un pad pad, que es una secuencia del tipo 1 0 1 0 1 0. Puede elegir una secuencia mejor, pero en términos generales, esta es una especie de secuencia predecible, que inserta aquí y cada vez que descifra el mensaje, se asegura de que esta secuencia todavía esté allí. La multiplicidad destruirá estos pedazos de almohadilla, y luego estará claro para usted que alguien desordenó su mensaje y lo descartó. Si estos bits permanecen en su lugar, esto prueba que nadie ha falsificado su mensaje y usted puede recibirlo, ya que alguien lo cifró correctamente.



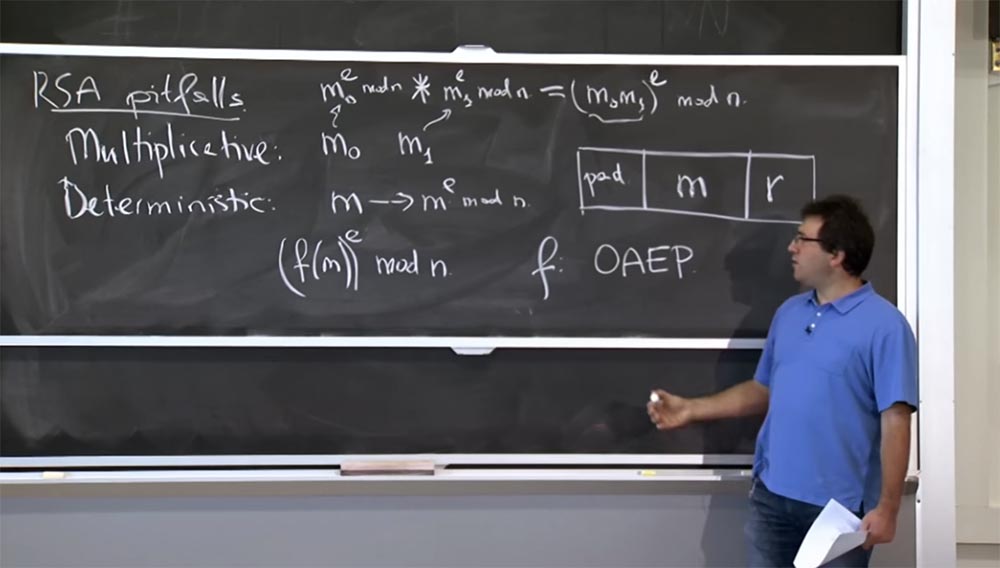Público: si un atacante sabe qué tan grande es el valor del pad, ¿puede establecer 1 en la parte inferior de la secuencia y luego multiplicar ese valor?

Profesor: sí, tal vez. Esto es un poco complicado, porque esta aleatoriedad continuará. Entonces, el diseño específico de este OAEP es un poco más complicado de lo que describí. Pero imagine que esto es un número entero en lugar de una multiplicación bit a bit, la aleatoriedad se extiende aún más, por lo que puede crear un esquema OAEP en el que esto no sucederá.

Resulta que no debe usar esta matemática RSA directamente, en la práctica debe usar algún tipo de biblioteca que implemente todas estas cosas para usted de la manera correcta, y usarla como un parámetro de cifrado y descifrado.

Sin embargo, los detalles discutidos anteriormente serán valiosos para nosotros, ya que en realidad estamos tratando de descubrir cómo romper o atacar la implementación de RSA existente.

En particular, el ataque descrito en el artículo de la conferencia aprovechará el hecho de que el servidor está a punto de probar este complemento de relleno cuando recibe el mensaje. Así es como vamos a considerar el tiempo que le tomará al servidor descifrar. Vamos a enviar un mensaje cuidadosamente construido, pero no se crea a partir del mensaje real my su encriptación. Vamos a crear un valor entero cifrado completo.

El servidor intentará descifrarlo y obtendrá algún tipo de absurdo, con el cual el pad pad probablemente no se emparejará, y el servidor rechazará inmediatamente este mensaje. , , , , : RSA, , . , . , .

, , RSA. , , , . , , , 1000 . e .



, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a ₁ ] mod p [ = a ₂ ] mod q, q – , .



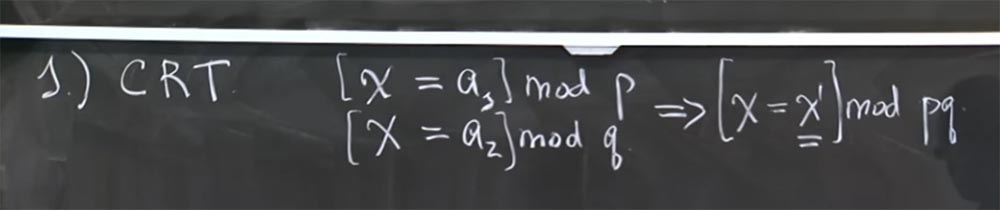
, [ = ¹ ] mod pq. ¹ , . ¹ , mod pq a ₁ a ₂ mod p q.

, ? , , n, p q.



, mod pq, mod p mod q. , , mod pq. , ? , , ?

: , ?

: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a ₁ ] mod p [ = a ₂ ] mod q , 4 . 2 RSA , .

, .

, Sliding windows, « ». . , .



, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .

c ^2x , : (c ^x ) ² :

c ^2x = (c ^x ) ²

c ^2x , 2 , cx, . , , c ^2x+1 :

c ^2x+1 = (c ^x ) ² x

.

, , , . , , , . , .

« », ? , . , , « » c ^2x+1 = (c ^x ) ² x .

, , , – , c ^2x+1 c ^2x , c. , , . , .



, :

1
3
7
...
31

. , , , .

, ^32x+y , 5 , 32- , ^y .



³² . , , , , c . «» .

29:00

Curso MIT "Seguridad de sistemas informáticos". 16: « », 2


.

Gracias por quedarte con nosotros. ¿Te gustan nuestros artículos? ¿Quieres ver más materiales interesantes? Apóyenos haciendo un pedido o recomendándolo a sus amigos, un descuento del 30% para los usuarios de Habr en un análogo único de servidores de nivel de entrada que inventamos para usted: toda la verdad sobre VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de $ 20 o cómo dividir el servidor? (las opciones están disponibles con RAID1 y RAID10, hasta 24 núcleos y hasta 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 veces más barato? Solo tenemos 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV desde $ 249 en los Países Bajos y los EE. UU. Lea sobre Cómo construir un edificio de infraestructura. clase utilizando servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?