Curso MIT "Seguridad de sistemas informáticos". Lección 16: Ataques a través del canal lateral, Parte 2

Instituto de Tecnología de Massachusetts. Conferencia Curso # 6.858. "Seguridad de los sistemas informáticos". Nikolai Zeldovich, James Mickens. Año 2014

Computer Systems Security es un curso sobre el desarrollo e implementación de sistemas informáticos seguros. Las conferencias cubren modelos de amenazas, ataques que comprometen la seguridad y técnicas de seguridad basadas en trabajos científicos recientes. Los temas incluyen seguridad del sistema operativo (SO), características, gestión del flujo de información, seguridad del idioma, protocolos de red, seguridad de hardware y seguridad de aplicaciones web.

Lección 1: "Introducción: modelos de amenaza" Parte 1 / Parte 2 / Parte 3
Lección 2: "Control de ataques de hackers" Parte 1 / Parte 2 / Parte 3
Lección 3: “Desbordamientos del búfer: exploits y protección” Parte 1 / Parte 2 / Parte 3
Lección 4: “Separación de privilegios” Parte 1 / Parte 2 / Parte 3
Lección 5: “¿De dónde vienen los sistemas de seguridad?” Parte 1 / Parte 2
Lección 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Lección 7: “Sandbox de cliente nativo” Parte 1 / Parte 2 / Parte 3
Lección 8: "Modelo de seguridad de red" Parte 1 / Parte 2 / Parte 3
Lección 9: "Seguridad de aplicaciones web" Parte 1 / Parte 2 / Parte 3
Lección 10: “Ejecución simbólica” Parte 1 / Parte 2 / Parte 3
Lección 11: "Ur / Lenguaje de programación web" Parte 1 / Parte 2 / Parte 3
Lección 12: Seguridad de red Parte 1 / Parte 2 / Parte 3
Lección 13: "Protocolos de red" Parte 1 / Parte 2 / Parte 3
Lección 14: "SSL y HTTPS" Parte 1 / Parte 2 / Parte 3
Lección 15: "Software médico" Parte 1 / Parte 2 / Parte 3
Lección 16: "Ataques de canal lateral" Parte 1 / Parte 2 / Parte 3

Audiencia: ¿cómo determinar x e y primero?

Profesor: para esto debes mirar al expositor en representación binaria. Supongamos que trato de calcular el valor de c ^1011010 , el grado también puede consistir en un mayor número de bits. Si queremos volver a cuadrar, entonces necesitamos mirar el bit más bajo, aquí está 0.



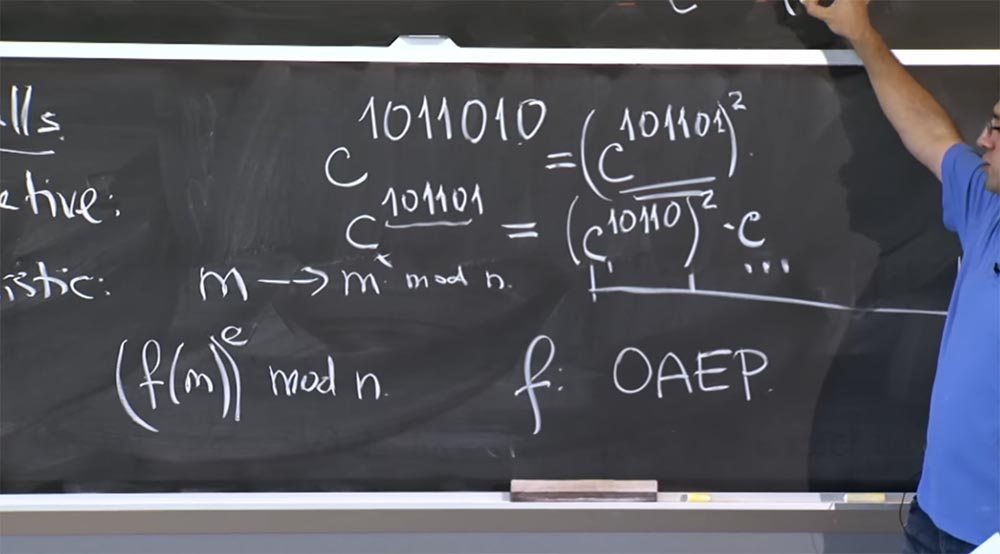
Por lo tanto, obtenemos la igualdad c ^1011010 = (c ¹⁰¹¹⁰¹ ) ²

A continuación, necesitamos calcular c ¹⁰¹¹⁰¹ , aquí no podemos usar esta regla, porque no es 2x, será x más 1. Por lo tanto, escribimos esta igualdad:

c ¹⁰¹¹⁰¹ = (c ¹⁰¹¹⁰ ) ² c, porque este prefijo 101101 = 10110 + 1.

Por lo tanto, multiplicamos el cuadrado por c, por lo que lo usamos para volver a cuadrado.

Para las "ventanas deslizantes" necesitamos capturar más bits del extremo inferior. Si quieres hacer un truco aquí con una "ventana deslizante" en lugar de extraer uno de aquí, entonces teniendo en cuenta esta enorme tabla, podemos tomar 3 bits a la vez, aferrándonos a c7. Si tomamos los primeros 3 bits de un grado, obtenemos c ¹⁰¹¹⁰¹ = (c ¹⁰¹ ) ⁸ c ¹⁰¹ .

En este caso, realmente tenemos la misma cantidad de cálculos para (c ¹⁰¹ ) ⁸ , pero puede ver el valor de c ¹⁰¹ en la tabla. Y la parte en forma de (c ¹⁰¹ ) ⁸ dice que va a usar "ventanas deslizantes" para calcular su valor.



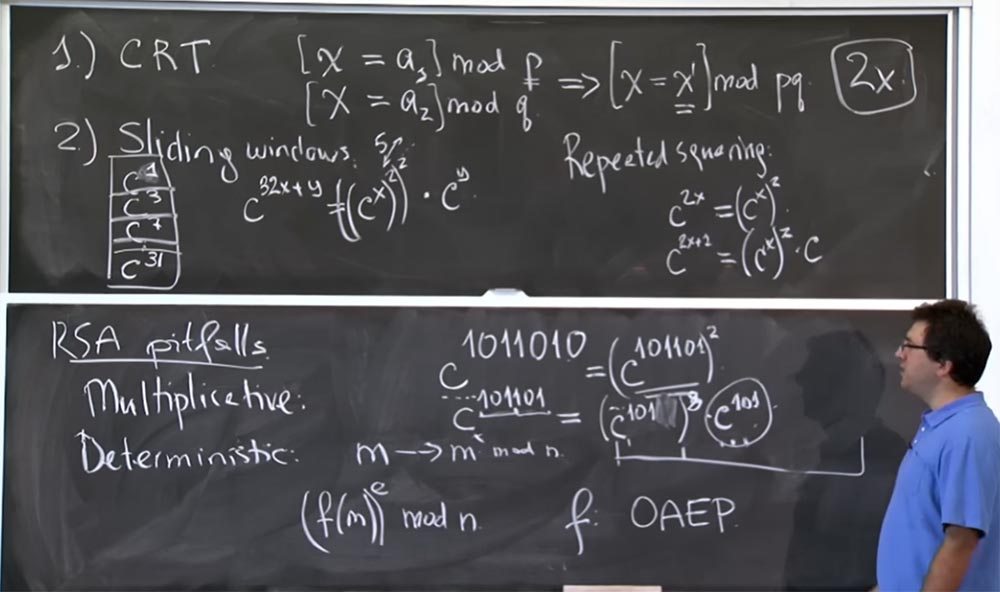
Esto ahorra mucho tiempo, ya que permite utilizar valores multiplicados previamente. Hace 10 años se creía que una tabla de valores de hasta 32 grados es el plan óptimo en términos de eficiencia computacional, porque hay algún tipo de compromiso aquí, ¿verdad? Dedica tiempo a crear esta tabla, pero no debería ser demasiado grande si no va a utilizar algunos registros con frecuencia. Suponga que si crea una tabla de valores de hasta c ⁵⁰⁰ grados, pero no va a utilizar exponentes con un valor superior a 128, simplemente pierda su tiempo.

Público: ¿hay alguna razón para no crear una mesa tan gigante de antemano? Es decir, calcular los valores de un número limitado de grados que se pueden eludir en los cálculos.

Profesor: si no desea realizar cálculos volumétricos por adelantado ... bueno, hay dos cosas. Una es que debe tener un código para verificar si el registro requerido en la tabla está lleno o no, y esto probablemente reducirá la precisión de la predicción de las ramas de los procesos de la CPU. Al mismo tiempo, en el caso general, el procesador funcionará más lentamente, ya que tendrá que verificar si el registro requerido está en la tabla. La segunda cosa, que es algo molesta, podría ser la pérdida de entradas de la tabla a través de varios canales laterales, es decir, a través de patrones de acceso a caché. Entonces, si tiene algún otro proceso ejecutándose en el mismo procesador, puede ver qué direcciones de caché se eliminan del caché o se ralentizan porque alguien tiene acceso a grabar c ³ o grabar c ³¹ . Y cuanto más grande sea esta tabla, más fácil será determinar qué bits de exponente se utilizan para crear la clave RSA.

Esta tabla gigante puede decir qué dirección de caché se perdió para el procesador, es decir, indica que el proceso de cifrado debe tener acceso a esta entrada en la tabla. A su vez, esto le indica que la secuencia de bits dada aparece en el exponente de su clave privada. Por lo tanto, supongo que matemáticamente puede completar esta tabla tanto como sea necesario, pero en la práctica no desea que resulte de un tamaño gigantesco. Además, no podrá utilizar eficazmente entradas de tabla enormes. Es mucho más útil usar los registros de una tabla relativamente pequeña repetidamente, por ejemplo, para calcular c ^7, puede usar el valor c ³ dos veces y así sucesivamente.

Por lo tanto, aquí está la optimización de RSA mediante el reencuadre y los métodos de "ventana deslizante". No sé si todavía usan este tamaño de "ventanas deslizantes", pero en cualquier caso, acelera el proceso de cálculo, porque de lo contrario tendría que cuadrar cada bit del exponente y luego multiplicarlo por cada bit. Por lo tanto, si tiene un exponente de 500 bits, entonces tendría que completar 500 cuadrados y aproximadamente 256 multiplicaciones por c. Con las "ventanas deslizantes" todavía tiene que hacer 512 cuadrados, porque esto no se puede evitar, pero el número de multiplicaciones por c disminuirá de 256 a aproximadamente 32 debido al uso de entradas de la tabla.

Este es el plan de optimización general, que acelera el proceso de cálculo aproximadamente una vez y media. Esta es una optimización bastante simple. Hay dos trucos inteligentes con números que hacen que el proceso de multiplicación sea más eficiente.

La primera es la transformación de Montgomery, en un segundo veremos por qué esto es especialmente importante para nosotros. Esta optimización está tratando de resolver un problema para nosotros, que es que cada vez que hacemos la multiplicación, obtenemos un número que continúa creciendo y creciendo en orden creciente. En particular, tanto en las "ventanas deslizantes" como en el nuevo cuadratura, en realidad multiplicaste 2 números juntos cuando elevaste c a la potencia de y.

El problema es que si los datos de entrada c ^x y c ^y para la multiplicación fueran, digamos, 512 bits cada uno, entonces el tamaño del resultado de la multiplicación sería 1000 bits. Después de eso, toma este resultado de 1000 bits y lo multiplica nuevamente por algo así como 512 bits, se convierte en el tamaño de 1500, 2000, 2500 bits y todo crece y crece.

Sin embargo, no desea esto, porque la multiplicación aumenta el orden de los números multiplicados. Debido a esto, debemos mantener el tamaño de nuestro número lo más pequeño posible, básicamente igual a 512 bits, porque todos estos cálculos son mod p o mod q.

Podemos reducir este número, por ejemplo, queremos calcular (((c ^x ) ² ) ² ) ² . Lo que podría hacer es, por ejemplo, calcular cx módulo p, luego volverlo al cuadrado nuevamente módulo p y nuevamente al cuadrado módulo p. Este método es relativamente bueno, porque nos permite mantener el tamaño de nuestro número dentro de 512 bits, es decir, lo más pequeño que podamos obtener. Esto es bueno en el sentido de reducir el tamaño de los números que necesitamos multiplicar, pero de hecho, la operación con este módulo p "aumenta significativamente el costo" del cálculo.



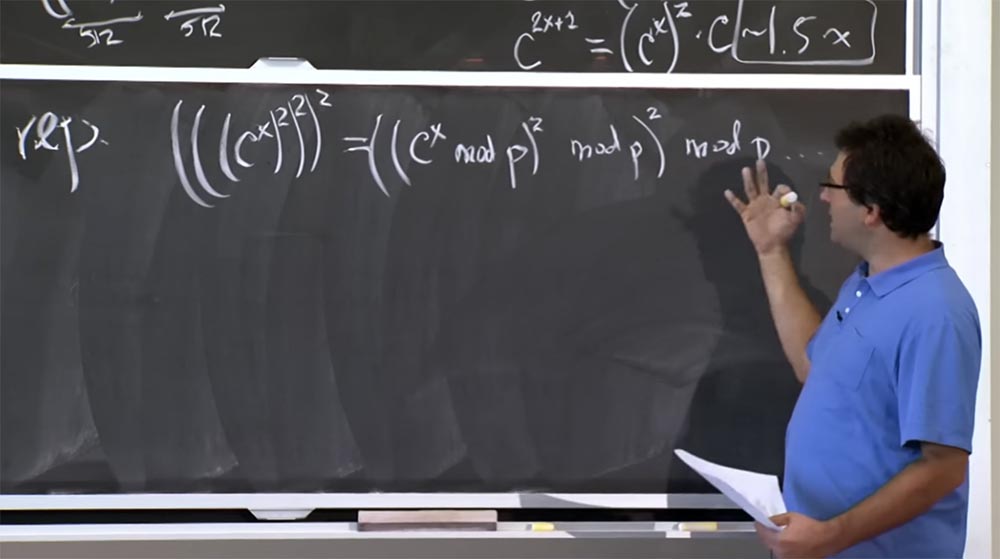
Porque la forma de obtener mod p es en división. Y la división es peor que la multiplicación. No enumeraré los algoritmos para la división, pero es muy lento. Por lo general, intenta evitar las operaciones de división siempre que sea posible, porque esta no es una programación fácil. El hecho es que necesita usar algún tipo de algoritmos de aproximación, métodos de Newton y similares, y todo esto ralentizará el proceso de cálculo.

La multiplicación es mucho más rentable, pero usar las operaciones mod p o mod q para reducir el tamaño de los números costará más que la multiplicación. Le mostraré una forma de evitar esto y cómo hacer cálculos rápidos utilizando la transformación Montgomery.

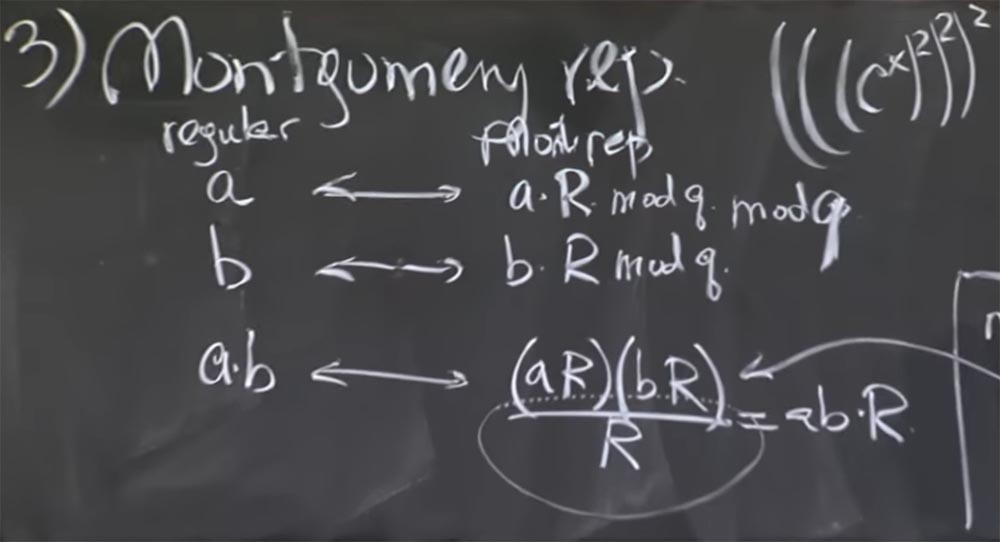
La idea básica es representar los enteros que vas a multiplicar en forma de transformación de Montgomery. Esto es realmente muy fácil. Para hacer esto, simplemente multiplicamos nuestro número a por un cierto valor mágico R. Después de un segundo te diré de qué se trata. Pero primero descubramos qué sucede cuando seleccionamos un valor arbitrario de R.

Entonces, tomamos 2 números, a y b, y los convertimos a la representación de Montgomery, multiplicando cada uno por R. Entonces el producto de a y b en la transformación de Montgomery se verá así:

ab <-> (aR) (bR) / R = abR

Es decir, multiplicas aR por bR y obtienes el producto de ab por R al cuadrado. Ahora tenemos dos R, esto es un poco molesto, pero puede dividirlo por R. Como resultado, obtenemos el producto de ab por R. No está claro por qué necesitábamos multiplicar este número una vez más. Primero descubramos si esto es correcto, y luego entenderemos por qué será más rápido.
Esto es correcto en el sentido de que es muy fácil. Si desea multiplicar algunos números, debe multiplicarlos por este valor de R y obtener la transformación Montgomery. Cada vez que multiplicamos estos 2 números, debemos dividirlos entre R y luego observar la forma resultante de la transformación de la forma abR. Luego, cuando terminemos de cuadrar, multiplicar y todas estas cosas, volveremos a la forma normal y ordinaria del resultado, simplemente dividiendo por R por última vez.



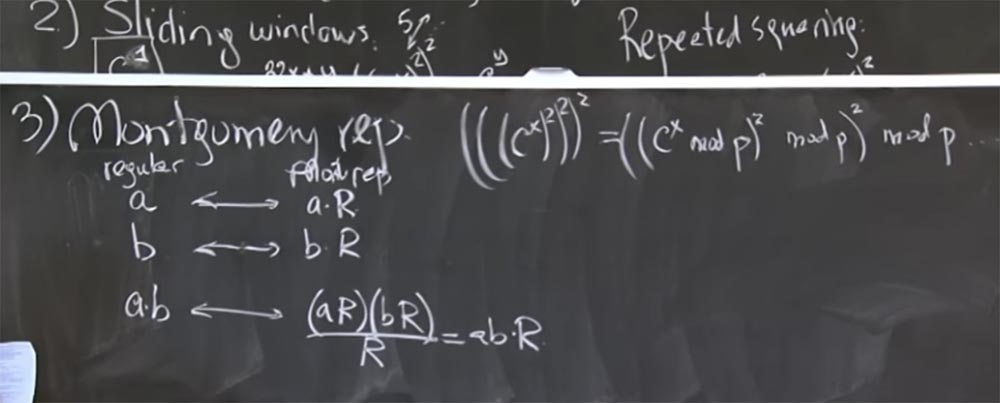
Ahora considere cómo elegir el número más adecuado para R para que la división por R sea una operación muy rápida. Y lo mejor aquí es que si la división por R es muy rápida cuando es un número pequeño, y no tenemos que hacer este mod q con demasiada frecuencia. En particular, aR, digamos, también tendrá un tamaño de aproximadamente 500 bits, porque todo esto es en realidad mod p o mod q. Por lo tanto, aR es de 500 bits, bR también será de 500 bits, de modo que el producto (aR) (bR) será de 1000 bits. R también será un número conveniente de 500 bits, el tamaño de p. Y si podemos hacer que la operación de división sea lo suficientemente rápida, entonces el resultado de ab también será aproximadamente un número de 500 bits, de modo que podamos multiplicar sin la necesidad de una división adicional. Dividir por R es mucho más rentable y nos da un pequeño resultado, lo que evita el uso de mod p en la mayoría de las situaciones.

Entonces, ¿cuál es este extraño número R del que estoy hablando todo el tiempo? Tiene un valor de 2 a 512 grados:

R = 2 ⁵¹²

Será 1 y un montón de ceros, por lo que es fácil multiplicar por ese número, porque es suficiente para agregar un montón de ceros al resultado. La división también puede ser simple si los bits menos significativos del resultado son cero. Entonces, si tiene un valor de un montón de bits acompañado de 512 ceros, dividir entre 2 y 512 grados será muy simple: simplemente coloca ceros en el lado derecho, y esta es una operación de división completamente correcta.

El pequeño problema es que en realidad no tenemos ceros en el lado derecho cuando haces esta multiplicación. Tenemos números reales de 512 bits con los 512 bits.

El producto de (aR) por (bR) también es un número real del orden de 1000 bits, por lo que no podemos soltar los bits menos significativos. Pero un enfoque razonable se basa en el hecho de que lo único que nos preocupa es el valor de mod p. Por lo tanto, siempre puede agregar múltiples p a este valor sin cambiar su equivalente de mod p. Como resultado, podemos agregar múltiplos de valores de p para que todos los bits menos significativos se conviertan en ceros. Veamos algunos ejemplos simples. No voy a escribir 512 bits en la pizarra, pero solo daré un breve ejemplo.

Supongamos que en nuestra situación R = 2 ⁴ = 10000. Este es un tamaño mucho más pequeño de lo que realmente es. Veamos cómo funciona esta transformación de Montgomery. Intentamos calcular mod q, donde q = 7. En forma binaria q = 7 es (111).

Supongamos además que realizamos alguna multiplicación (aR) (bR), y en representación binaria el resultado es 11010, es decir, este será el valor del producto (aR) (bR). ¿Cómo lo dividimos por R?

Obviamente, no los cuatro bits menos significativos son ceros, por lo que no podemos separarlos, sino que podemos agregar cantidades que son múltiplos de q. En particular, podemos agregar 2 veces en q, con 2q = 1110 en representación binaria. Como resultado de la suma, obtenemos 101000, espero haber hecho todo bien.



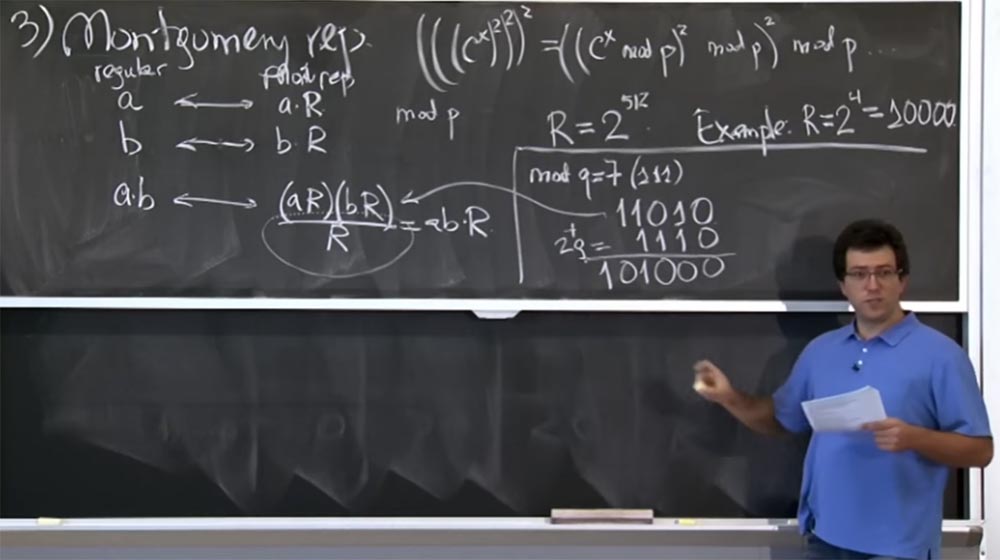
Entonces obtuvimos la suma (aR) (bR) + 2q. De hecho, no nos importa + 2q, porque lo único que nos importa es el valor de mod q. Ahora estamos más cerca de la meta, porque tenemos tres ceros a la derecha. Ahora podemos agregar más q. Digamos que esta vez será 8q, que será 111000. Nuevamente, sume nuestras líneas y obtenga 1100000. Ahora tenemos el original (aR) (bR) + 2q + 8q = 1100000. Finalmente, podemos dividir esto fácilmente en R, solo bajando cuatro ceros bajos.



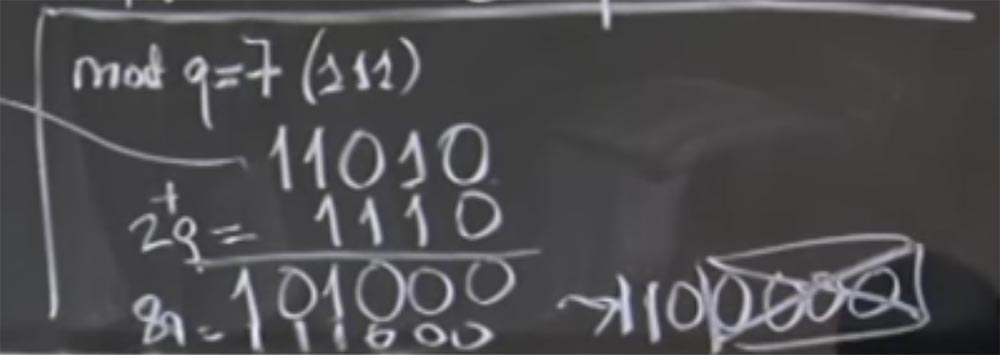Audiencia: ¿el producto (aR) (bR) siempre terminará con 1024 ceros?

Profesor: no, y explicaré cuál podría ser la confusión. Digamos que el número a es 512 bits, lo multiplicamos por R y obtuvimos un número de 1000 bits. En este caso, tiene razón, aR es el número en el que los bits altos son a, y los bits bajos son todos ceros. Pero luego ejecutamos mod q para hacerlo más pequeño. Por lo tanto, el tamaño de 1024 bits es generalmente una coincidencia, ya que este número tiene estos ceros bajos solo durante la primera conversión, pero después de hacer algunas multiplicaciones, serán bits arbitrarios.

Para no confundirlo, tuve que escribir mod q aquí después de aR y después de bR, aquí lo estoy agregando, y calcular este mod q tan pronto como realice la conversión para reducir el valor.



La conversión inicial es bastante laboriosa, o al menos tan costosa como la modulación convencional en la multiplicación. Lo bueno es que pagas este precio una vez cuando haces la conversión de Montgomery, y luego, en lugar de volver a convertirlo en cada paso de los cálculos, simplemente lo mantienes en forma de vista de Montgomery.
Recuerda que para elevar a una potencia que tiene 512 bits, tendrás que hacer más de 500 multiplicaciones, porque tenemos que hacer al menos 500 cuadrados y algunos más. Entonces haces mod q dos veces y luego obtienes muchas operaciones de división simples si te quedas en esta forma de representar números. Y al final, haces una división por R para volver a esta forma ab.

Entonces, en lugar de hacer mod q 500 veces para cada paso de la multiplicación, haces mod q dos veces y luego continúas haciendo estas divisiones por R a un costo mínimo.
Público: cuando agrega múltiplos de q y luego divide por R, ¿tenemos un resto?
Profesor: en realidad mod q significa el resto cuando se divide por q. En pocas palabras, x + yq mod q = x. En este caso, hay otra propiedad útil: que todos los módulos son primos. Esto es tan cierto como el hecho de que si tiene (x + yq / R) mod q, entonces es igual a x / R mod q.



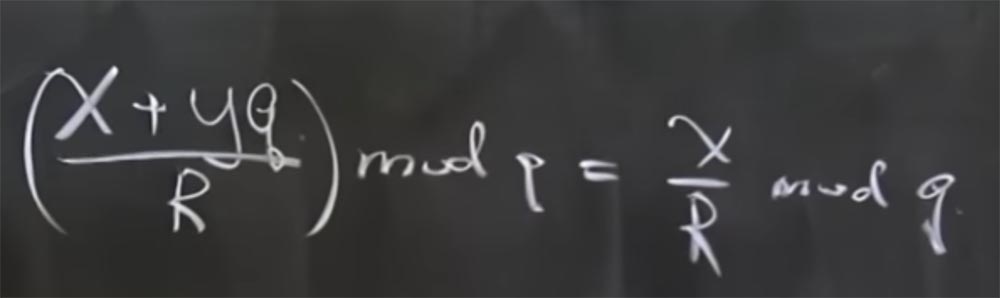
La razón para pensarlo es que no hay operaciones de división real en aritmética modular, es solo inversión. De hecho, esto significa que si tenemos (x + yq) multiplicado por R invertido calculado por mod q, entonces es igual a la suma de dos productos: el producto x del R invertido por mod q y el producto de yq por el R invertido por mod q. Además, el último término se reduce, porque es algo multiplicado por q.



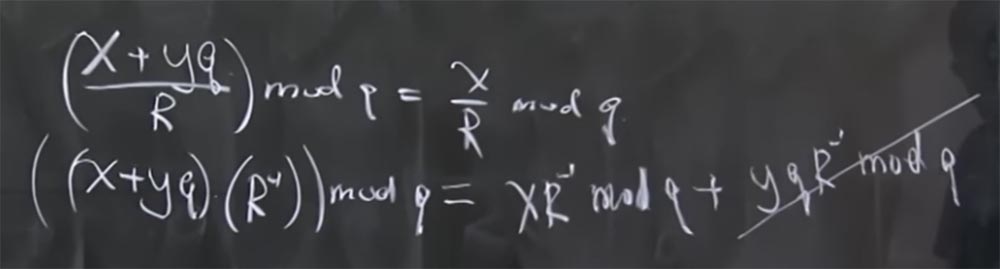
Para cosas como sumar 2q, 8q, etc., existe una fórmula que acelera el proceso de cálculo. Lo hice gradualmente, primero calculé 2q, luego 8q y así sucesivamente, pero los materiales de la conferencia tienen una fórmula completa que se puede usar, simplemente no quiero perder el tiempo escribiéndolo en la pizarra. Le permite calcular qué valor de múltiplo de q debe agregar para que todos los bits menos significativos se conviertan en 0. Luego resulta que para hacer la división por R, solo necesita calcular este múltiplo mágico de q, agregarlo y luego descartar el valor bajo cero bits, y esto devolverá su número a 512 bits sin importar el tamaño del resultado que obtenga.

Pero hay una sutileza. La única razón por la que estamos hablando de esto es porque algo extraño está sucediendo aquí, lo que nos permite encontrar información sobre los tiempos. En particular, aunque dividimos por R, todavía sabemos que el resultado será de aproximadamente 512 bits. Pero aún puede ser más que q, porque q no es un número de 512 bits, puede ser ligeramente menor que R.

Entonces puede ser que después de hacer esta división ventajosa por R, tengamos que restar q nuevamente, porque obtenemos algo pequeño, pero aún no lo suficientemente pequeño. Entonces existe la posibilidad de que después de esta división tengamos que restar q nuevamente. Y esta resta se puede usar como parte del ataque, porque la operación de resta agrega el tiempo de cálculo.



Y alguien descubrió, no estos tipos, sino alguien en el trabajo anterior, que existe la posibilidad de hacer algo llamado reducción adicional o reducción adicional. , . , xd mod q, - x mod q, 2R. .



, x mod q , . , cd.



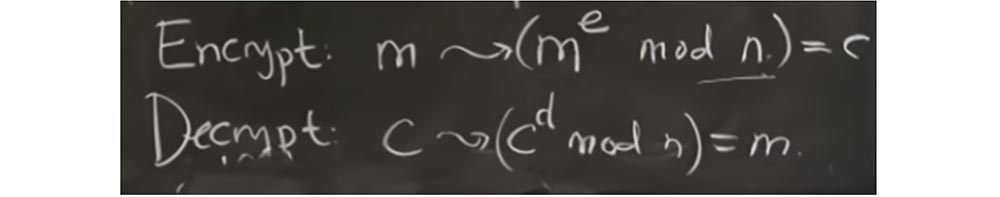
, extra reduction , X , , , q.



, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .

: , ?

: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



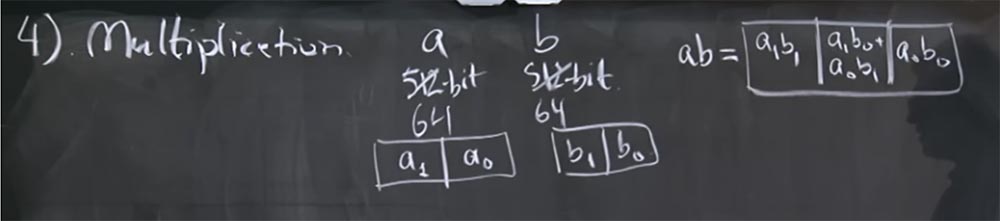
55:00

Curso MIT "Seguridad de sistemas informáticos". 16: « », 3


La versión completa del curso está disponible aquí .

Gracias por quedarte con nosotros. ¿Te gustan nuestros artículos? ¿Quieres ver más materiales interesantes? Apóyenos haciendo un pedido o recomendándolo a sus amigos, un descuento del 30% para los usuarios de Habr en un análogo único de servidores de nivel de entrada que inventamos para usted: toda la verdad sobre VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de $ 20 o cómo dividir el servidor? (las opciones están disponibles con RAID1 y RAID10, hasta 24 núcleos y hasta 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps hasta diciembre de forma gratuita al pagar por un período de seis meses, puede ordenar aquí .

Dell R730xd 2 veces más barato? Solo tenemos 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV desde $ 249 en los Países Bajos y los EE. UU. Lea sobre Cómo construir un edificio de infraestructura. clase utilizando servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?