Curso MIT "Seguridad de sistemas informáticos". Lección 16: "Ataques de canal lateral", Parte 3

Instituto de Tecnología de Massachusetts. Conferencia Curso # 6.858. "Seguridad de los sistemas informáticos". Nikolai Zeldovich, James Mickens. Año 2014

Computer Systems Security es un curso sobre el desarrollo e implementación de sistemas informáticos seguros. Las conferencias cubren modelos de amenazas, ataques que comprometen la seguridad y técnicas de seguridad basadas en trabajos científicos recientes. Los temas incluyen seguridad del sistema operativo (SO), características, gestión del flujo de información, seguridad del idioma, protocolos de red, seguridad de hardware y seguridad de aplicaciones web.

Lección 1: "Introducción: modelos de amenaza" Parte 1 / Parte 2 / Parte 3
Lección 2: "Control de ataques de hackers" Parte 1 / Parte 2 / Parte 3
Lección 3: “Desbordamientos del búfer: exploits y protección” Parte 1 / Parte 2 / Parte 3
Lección 4: “Separación de privilegios” Parte 1 / Parte 2 / Parte 3
Lección 5: “¿De dónde vienen los sistemas de seguridad?” Parte 1 / Parte 2
Lección 6: “Oportunidades” Parte 1 / Parte 2 / Parte 3
Lección 7: “Sandbox de cliente nativo” Parte 1 / Parte 2 / Parte 3
Lección 8: "Modelo de seguridad de red" Parte 1 / Parte 2 / Parte 3
Lección 9: "Seguridad de aplicaciones web" Parte 1 / Parte 2 / Parte 3
Lección 10: “Ejecución simbólica” Parte 1 / Parte 2 / Parte 3
Lección 11: "Ur / Lenguaje de programación web" Parte 1 / Parte 2 / Parte 3
Lección 12: Seguridad de red Parte 1 / Parte 2 / Parte 3
Lección 13: "Protocolos de red" Parte 1 / Parte 2 / Parte 3
Lección 14: "SSL y HTTPS" Parte 1 / Parte 2 / Parte 3
Lección 15: "Software médico" Parte 1 / Parte 2 / Parte 3
Lección 16: "Ataques de canal lateral" Parte 1 / Parte 2 / Parte 3

Público: ¿Utiliza el método Karatsuba?

Profesor: sí, este es un método de multiplicación inteligente que no requiere cuatro etapas de cálculo. El método Karatsuba se enseña en el curso .601, o ¿cómo se designa hoy?

Audiencia: 042.

Profesor: 042, excelente. Sí, este es un muy buen método. Casi todas las bibliotecas criptográficas lo usan. Para aquellos de ustedes que no son graduados de nuestro instituto, lo digo porque tenemos estudiantes graduados aquí, escribiré sobre el método Karatsuba en la pizarra. Aquí necesita calcular tres valores:

a ₁ b ₁
(a ₁ - a ₀ ) (b ₁ - b ₀ )
a ₀ b ₀

Por lo tanto, haces 3 multiplicaciones en lugar de cuatro, y resulta que puedes restaurar este valor a ₁ b ₀ + a ₀ b _{1 a} partir de estos tres resultados de multiplicación.



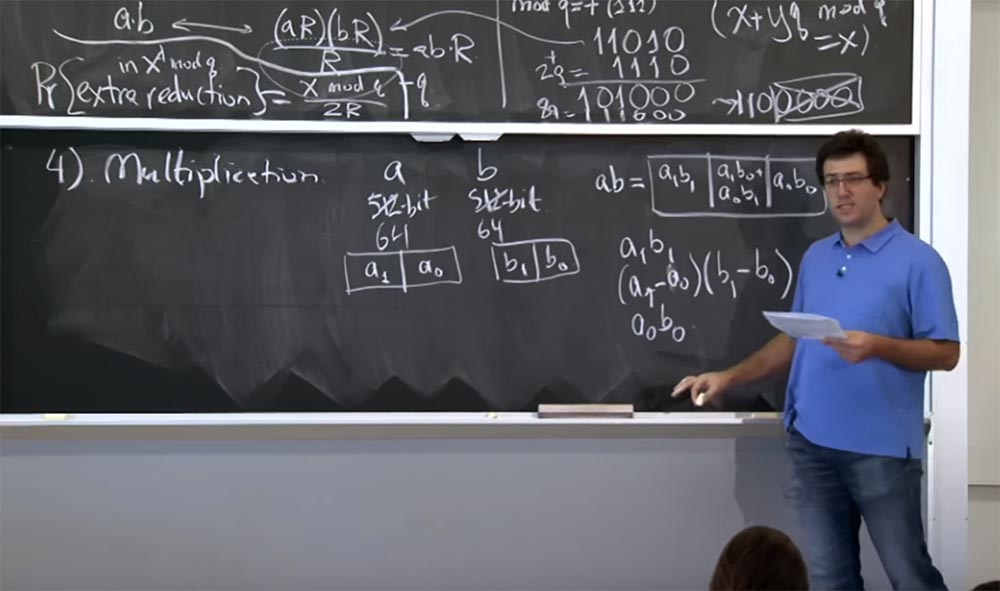
La forma especial de hacer esto es esto ... déjame ponerlo en una forma diferente.

Entonces, tendremos:

(2 ⁶⁴ + 2 ³² ) (a ₁ b ₁ ) +
(2 ³² ) (- (a ₁ - a ₀ ) (b ₁ - b ₀ )
(2 ³² + 1) (a ₀ b ₀ )

Esto no está muy claro, pero si calcula los detalles, en última instancia, convénzase usted mismo de que este valor en estas 3 líneas es equivalente a ab, pero al mismo tiempo reduce el cálculo en una multiplicación. Y la forma en que aplicamos esto a multiplicaciones más voluminosas es que continúas bajando recursivamente. Entonces, si tiene valores de 512 bits, puede dividirlos en una multiplicación de 256 bits. Haces tres multiplicaciones de 256 bits, cada vez de forma recursiva utilizando el método Karatsuba. Al final, sus cálculos se reducen al tamaño de la máquina y pueden procesarse mediante una sola instrucción de máquina.



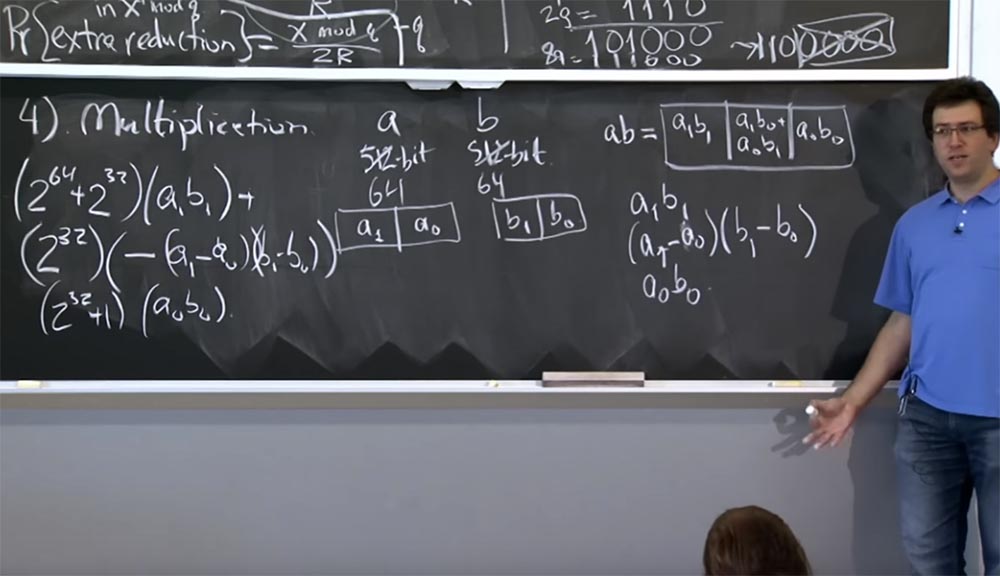
Entonces, ¿dónde está el ataque de tiempo? ¿Cómo usan estos muchachos la multiplicación de Karatsuba? Resulta que OpenSSL está preocupado por dos tipos de multiplicación que podría tener que hacer.
El primero es la multiplicación de dos números grandes de aproximadamente el mismo tamaño. Esto sucede muchas veces cuando realizamos una exponenciación modular, porque todos los valores que multiplicaremos tendrán un tamaño de aproximadamente 512 bits. Por lo tanto, cuando multiplicamos c por y o cuadrado, multiplicamos dos cosas de aproximadamente el mismo tamaño. En este caso, el método Karatsuba tiene mucho sentido, ya que reduce el tamaño de los números al cuadrado en aproximadamente 1,58 veces, lo que acelera enormemente el proceso de cálculo.
El segundo tipo de multiplicación es cuando OpenSSL multiplica dos números cuyo tamaño difiere significativamente entre sí: uno es muy grande y el otro es muy pequeño. En este caso, también podría usar el método Karatsuba, pero funcionará más lentamente que la multiplicación primitiva. Suponga que multiplica un número de 512 bits por un número de 64 bits, tendrá que elevar cada bit del primer número a una potencia de 64, lo que resulta en una desaceleración del proceso 2n en lugar de una aceleración n / 1.58. Por lo tanto, estos tipos que usan OpenSSL intentaron hacerlo de manera más inteligente, y fue aquí donde comenzaron los problemas.

Decidieron que cambiarían dinámicamente entre el método efectivo de Karatsuba y el método de multiplicación de la escuela primaria. Su heurística fue la siguiente. Si los dos números que multiplica consisten en el mismo número de palabras de máquina, o al menos tienen el mismo número de bits que las unidades de 32 bits, entonces se utiliza el método Karatsuba. Si dos números difieren mucho en tamaño entre sí, al cuadrado o directo simple, se realiza la multiplicación normal.

En este caso, puede realizar un seguimiento de cómo se produce el cambio a otro método de multiplicación. Dado que el momento del cambio no pasa sin dejar rastro, después se notará si ahora requiere mucho más tiempo para la multiplicación o mucho menos que antes. Los investigadores aprovecharon esta circunstancia para organizar un ataque utilizando el método de sincronización.

Creo que he terminado de contarte todos los trucos extraños que las personas usan cuando implementan RSA en la práctica. Ahora intentemos juntarlos y usarlos en relación con todo el servidor web para descubrir cómo puede "pellizcar" los bits que nos interesan del paquete de red de entrada.

Si recuerda de la conferencia sobre HTTPS, el servidor web tiene una clave secreta. Utiliza esta clave secreta para demostrar que es el propietario correcto de todos los certificados a través de HTTPS o TLS. Esto se debe al hecho de que los clientes envían algunos bits seleccionados al azar, estos bits se cifran con la clave pública del servidor y el servidor descifra este mensaje con el protocolo TLS. Y si se marca el mensaje, estos bits aleatorios se utilizan para establecer una sesión de comunicación.

Pero en nuestro caso, este mensaje no se verificará, porque se creará de una manera especial, y cuando resulte que los bits adicionales no coinciden, el servidor devolverá un error tan pronto como termine de descifrar nuestro mensaje.

Esto es lo que vamos a hacer aquí. El servidor, puede suponer que es Apache con SSL abierto, recibirá un mensaje del cliente que considera como texto cifrado o algún texto cifrado hipotético que el cliente creó. Lo primero que hacemos con el texto cifrado c es descifrarlo usando la fórmula con → (c ^d mod n) = m.

Si recuerda la primera optimización, aplicaremos el teorema del resto chino y dividiremos nuestro texto en dos partes: una para calcular por mod p, la otra por mod q, y luego combinar los resultados. Primero, tome c y represente en dos cantidades: la primera se llama c ₀ , será igual a mod q, y la segunda es c ₁ , y será igual a c mod p. Luego haremos lo mismo para calcular c para d mod p y c para d mod q.



A continuación, vamos a cambiar a la vista Montgomery porque esto hará que nuestras multiplicaciones sean muy rápidas. Entonces, lo siguiente que SSL hará con su número es calcular c ₀ ', que será igual a c ₀ R mod q y hacer lo mismo a continuación para el valor c1, no escribiré esto porque se ve igual .

Ahora que hemos cambiado a la forma de Montgomery, finalmente podemos realizar nuestras multiplicaciones, y aquí usaremos la técnica de "ventana deslizante". Tan pronto como obtengamos c ₀ ', hacemos este simple aumento de c ₀ ' a la potencia de d en mod q. Y aquí, dado que calculamos este valor para d, usaremos "ventanas deslizantes" para los bits del exponente d, y también usaremos el método Karatsuba o la multiplicación habitual, dependiendo del tamaño de nuestros operandos.



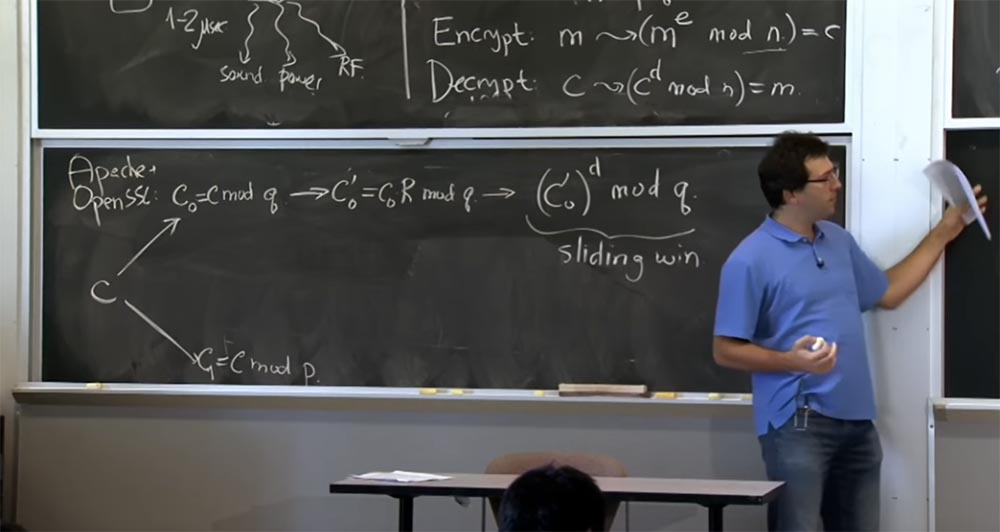
Entonces, si resulta que este valor c ₀ 'y el resultado de cuadratura obtenido previamente son del mismo tamaño, usamos el método Karatsuba. Si c ₀ 'es muy pequeño, y el resultado previo de la multiplicación es grande, entonces cuadraremos y multiplicaremos de la manera usual. Aquí usamos "ventanas deslizantes" y el método Karatsuba en lugar de la multiplicación normal.



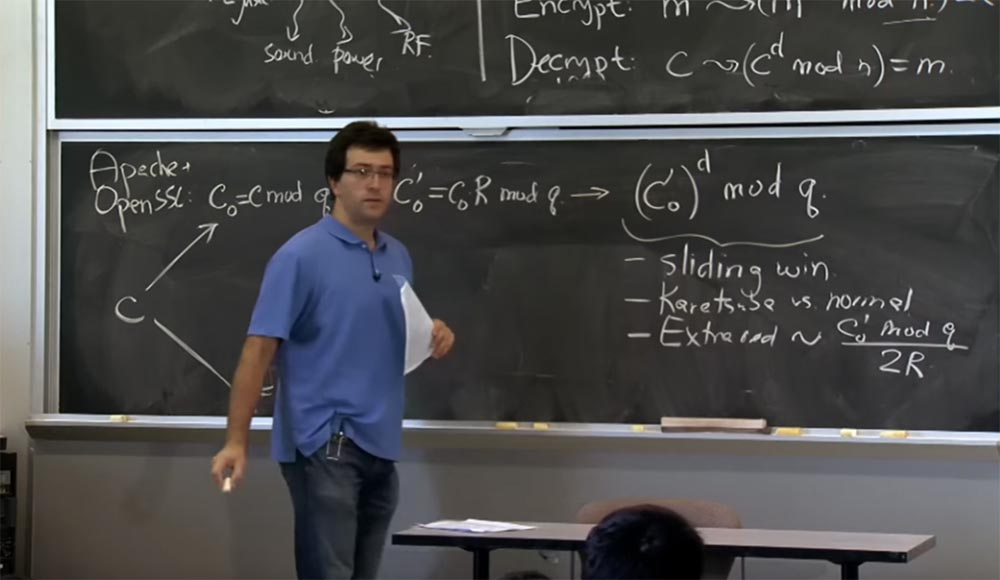
También en esta etapa, aparecen reducciones adicionales. Porque con cada multiplicación, las reducciones adicionales serán proporcionales a lo que elevamos a la potencia de mod q, es decir, el valor de (c ₀ ') ^d . Aquí, con una conexión simple de la fórmula, la probabilidad de reducciones adicionales será proporcional al valor c ₀ 'mod q dividido por 2R. Es en este lugar donde aparece un bit que afecta el tiempo.

De hecho, hay dos efectos posibles: usar el método Karatsuba en lugar de la multiplicación normal y la aparición de abreviaturas adicionales que vas a hacer.

En un segundo verás cómo se puede usar. Ahora, cuando obtenga este resultado para mod q y obtenga un resultado similar para mod p, finalmente puede recombinar estas dos partes en la parte superior e inferior y usar CRT, el teorema del resto chino.

Y lo que obtienes de la CRT como resultado ... lo siento, creo que primero debemos convertir esto desde el formulario de Montgomery. Por lo tanto, antes de la recombinación, convertimos la parte superior a la expresión (c ₀ ') ^d / R mod q y devolvemos nuestro valor cd mod q. En la parte inferior, en consecuencia, obtenemos cd mod p.

Ahora puede usar CRT para obtener el valor de c ^d mod n. Perdón por la fuente pequeña, no tenía suficiente pizarra. Aproximadamente lo mismo que obtenemos aquí abajo con ₁ , y finalmente podemos obtener nuestro resultado, es decir, el mensaje m.



Por lo tanto, el servidor toma un paquete entrante que recibe, lo ejecuta a través de toda esta tubería, ejecuta dos partes de esta tubería y termina con un mensaje descifrado m igual a cd mod m. Luego revisará el relleno de esta publicación. En el caso de nuestro ataque específico, creamos de tal manera que, de hecho, esta adición no coincidirá. Elegimos el valor c para las heurísticas que no cifran el mensaje real con la adición de relleno correcta.

Por lo tanto, el complemento no pasa la prueba, el servidor deberá registrar un error, enviar un mensaje de error al cliente y desconectarse. Por lo tanto, vamos a medir el tiempo que le tomará al servidor pasar nuestro mensaje a través de esta tubería. ¿Tiene alguna pregunta sobre el proceso de procesamiento de un mensaje por parte del servidor y la combinación de todas estas optimizaciones?

Público: en mi opinión, hay un error con un índice de magnitud c.

Profesor: sí, tienes razón, estoy agregando el índice 0, aquí debería estar c ₀ ^d mod q.



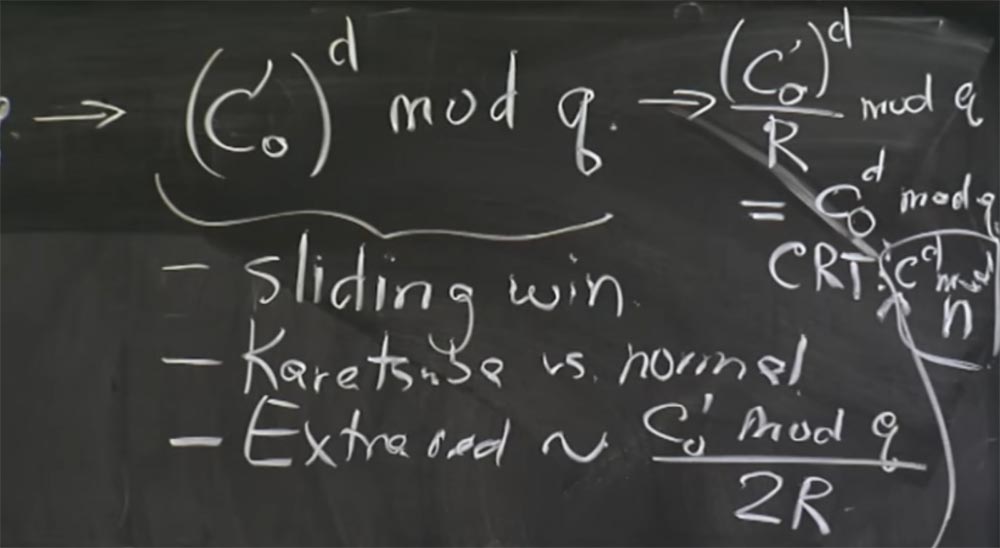Público: cuando divide por R mod q, ¿no hay suposiciones sobre cuánto q debe agregar para reducir aún más los bits bajos a ceros?

Profesor: sí, tiene razón, en esta etapa final (c ₀ ') ^d / R mod q puede haber reducciones adicionales. Entonces deberíamos hacer esta división por R de la manera correcta, y probablemente deberíamos hacer lo mismo que hacer la reducción de Montgomery aquí, cuando dividimos por R, para convertir el valor nuevamente. Dado que al comienzo de los cálculos no está claro exactamente cuánto q deberíamos agregar, usamos el método de selección, destruimos los ceros bajos, luego nuevamente hacemos mod q y, posiblemente, una reducción adicional. Tiene toda la razón, en este caso es exactamente la misma división por R mod q que para cada paso de la multiplicación de Montgomery.

Entonces, ¿cómo aprovechar esto? ¿Cómo puede un atacante resolver la clave secreta de un servidor midiendo el tiempo que lleva completar las operaciones? Estos tipos tienen un plan que se basa en adivinar un bit de clave privada a la vez. Podemos suponer que la clave secreta es el exponente encriptado d, porque conoce e y sabe n, esta es la clave pública. Lo único que no sabes es d.



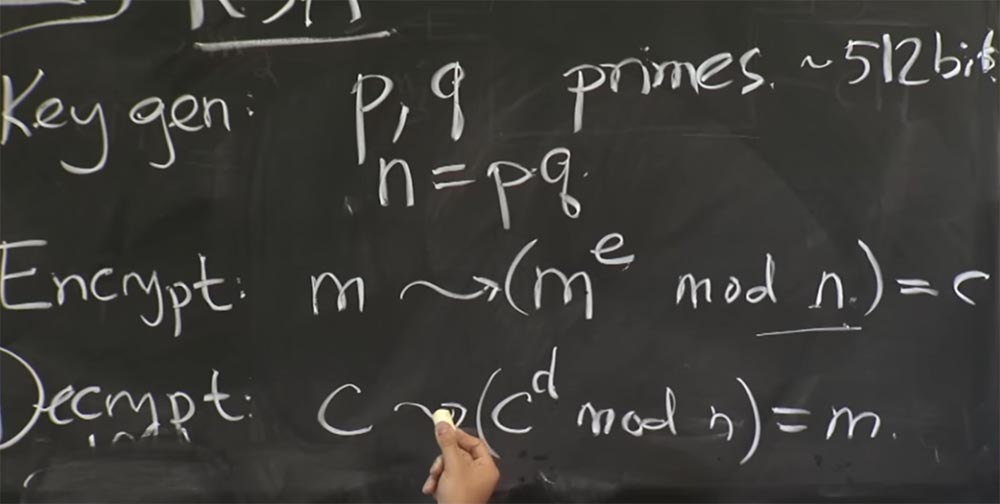
De hecho, en este ataque, no adivinan directamente el valor de d, ya que es bastante complicado. En cambio, consideran qop, sin importar cuál de estas dos cantidades. Una vez que adivine lo que importa, puede calcular n = pq. Luego, si conoce los valores de p y q, puede calcular la función φ de la que hablamos anteriormente. Esto le permitirá obtener el valor de d del valor de e. Por lo tanto, esta factorización del valor de n es extremadamente importante; debe mantenerse en secreto para garantizar la seguridad de RSA.

De hecho, estos tipos intentaron adivinar el valor q analizando los tiempos de esta tubería. ¿Qué están haciendo para esto? Seleccionan cuidadosamente el valor inicial del valor de c y miden el tiempo de su paso a través de la tubería del servidor.

En particular, hay dos partes en este ataque, y debes tomar algunos pasos iniciales para adivinar los primeros bits. Luego, tan pronto como tenga los primeros bits, puede adivinar el siguiente. Por lo tanto, déjame no contarte en detalle cómo adivinan los primeros bits, porque de hecho es mucho más interesante considerar cómo adivinan el siguiente bit. Si tenemos tiempo, volveremos a cómo se describe la suposición de varios bits iniciales en un artículo de conferencia.

Entonces, suponga que tiene la suposición g sobre qué bits están en el valor de esta q. Deje que este valor consista en tales bits: g = g ₀ g ₁ g ₂ ... y así sucesivamente. Más bien, ni siquiera es g, sino los bits reales de q, así que permítanme reescribirlo así: g = q ₀ q ₁ q ₂ ... Creemos que estos q son bits altos, y estamos tratando de adivinar los bits cada vez más bajos. Supongamos que conocemos el valor de q hasta el bit qj, y luego siguen todos los ceros. No tienes idea de cuáles son el resto de los bits.



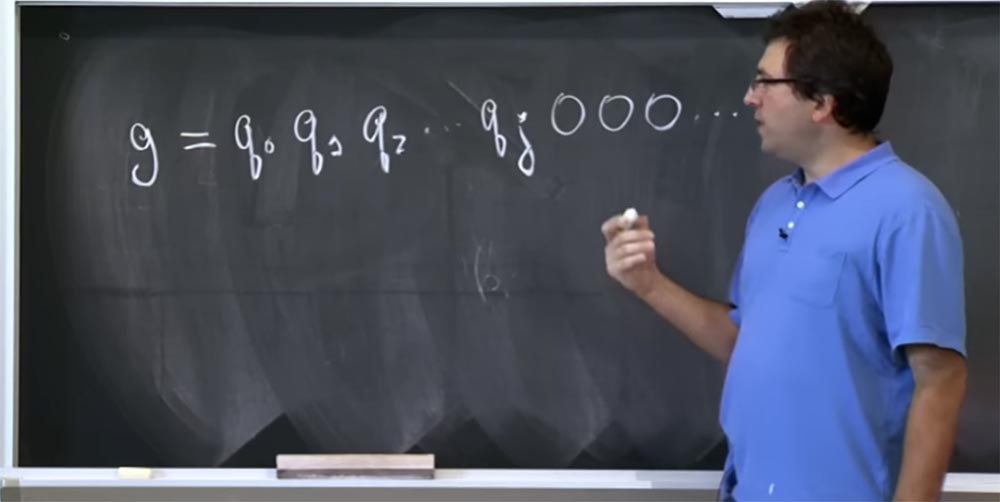
Estos tipos intentaron inyectar esta conjetura g en este lugar de nuestra tubería: (c0 ') d mod q. Porque este es el lugar donde se usan dos tipos de optimización: el método Karatsub en lugar de la multiplicación habitual y un número diferente de abreviaturas adicionales dependiendo del valor de c ₀ '. En realidad, intentaron introducir dos conjeturas diferentes en este lugar de la tubería: la primera, que parece g = q ₀ q ₁ q ₂ ... qj 000 ... 0000, y la segunda, que llamaron g _high , que consiste en los mismos bits altos, pero en su lugar De todos los ceros al final hay una unidad que indica un bit alto, seguido de ceros nuevamente:

g = q ₀ q ₁ q ₂ ... qj 100 ... 0000.

¿Cómo ayuda esto a estos muchachos a entender lo que está sucediendo? Hay dos formas de hacer esto. Supongamos que nuestra suposición g es igual al valor c ₀ '. Podemos suponer que estos g y g _altos corresponden al valor c ₀ 'dado en el tablero izquierdo. En realidad, es bastante simple hacer esto, porque c ₀ 'es bastante fácil de calcular hacia atrás a partir del valor de entrada cifrado c ₀ , simplemente lo multiplica por R.



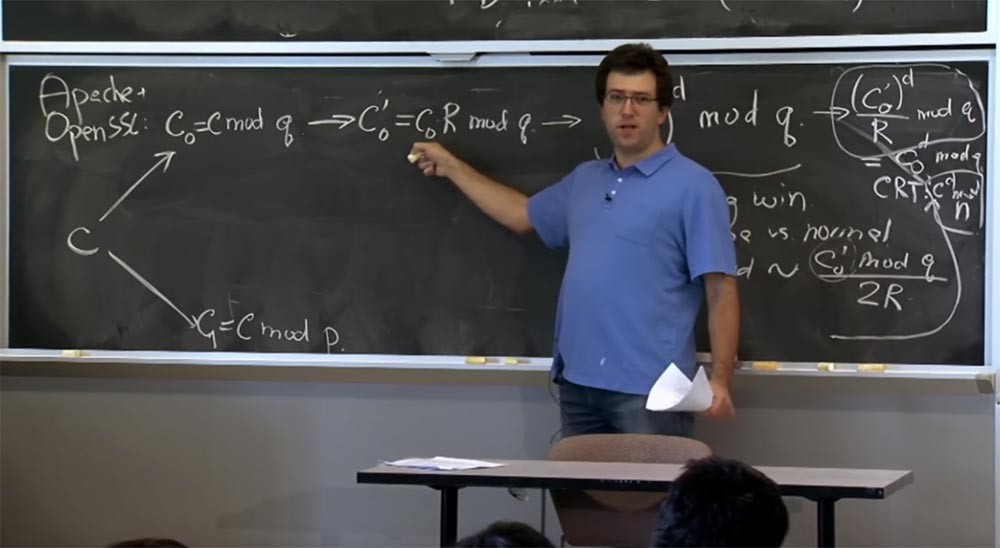
Por lo tanto, para adivinar el valor (c ₀ ') ^d , solo necesitan adivinar, adivinar g, y primero dividirlo por R, es decir, dividir por 512 mod algo allí. Luego lo volverán a presentar, el servidor lo multiplicará por R y continuará el proceso descrito en nuestro esquema de canalización.

Entonces, supongamos que pudimos poner nuestro valor entero particular seleccionado en el lugar correcto. Entonces, ¿cuál será el tiempo de cálculo c ₀ 'a d mod q?



Hay dos opciones posibles donde q encaja en esta imagen. Puede ser que q esté entre estos dos valores de gyg _alto , porque el siguiente bit de q es 0. Por lo tanto, este valor, el primer 0 después de qj, será menor que q, pero este valor, 1 después de q, será mayor que q. Esto sucede si el siguiente bit de q es 0, o es posible que q esté por encima de estos dos valores si el siguiente bit de q es 1.



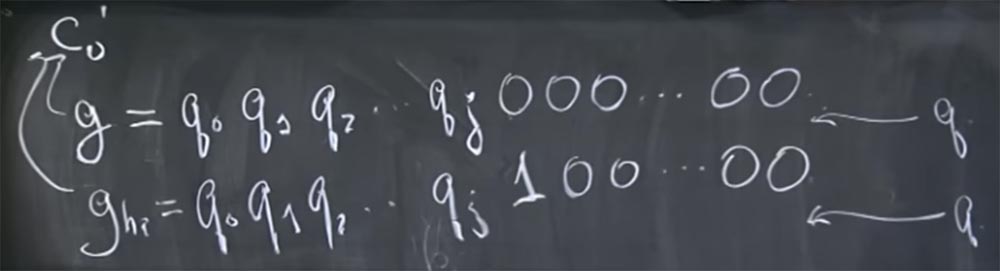
Ahora podemos decir cuál será el tiempo de descifrado de estos dos valores si q se encuentra entre ellos, o si q se encuentra por encima de ambos.

Veamos la situación donde q se encuentra arriba. En este caso, todo es más o menos lo mismo. Dado que ambos valores son menores que q, el valor de estas cosas en mod q será aproximadamente el mismo. Son ligeramente diferentes debido a este bit extra, pero aún más o menos del mismo tamaño. Y el número de reducciones adicionales, reducción adicional, probablemente tampoco diferirá mucho, porque es proporcional al valor de c0 'mod q. Y para ambos valores _altos g y g menores que q, todos son casi iguales. Ninguno de ellos excederá q y no causará una gran cantidad de reducciones adicionales, porque para q mayor que ambas conjeturas, el número de cálculos por el método Karatsuba con respecto al número de cálculos ordinarios seguirá siendo el mismo. En términos de esta relación, el servidor manejará g y g _{high por} igual. Por lo tanto, el servidor está a punto de crear aproximadamente la misma cantidad de abreviaturas adicionales para ambos valores. Por lo tanto, si ve que el servidor está pasando el mismo tiempo respondiendo a estas suposiciones, entonces probablemente debería suponer que realmente hay 1 en el valor _{alto de} g en este punto.



Por otro lado, si q se encuentra entre estos dos valores, entonces hay dos cosas posibles que pueden causar cambios de conmutación y sincronización. Una de las cosas es que dado que g _{high es} ligeramente mayor que q, el número de cortes adicionales será proporcional a c ₀ 'mod q, que es muy pequeño, porque c ₀ ' es q más algunos bits en esta secuencia adicional de 100 ... 00. Por lo tanto, el número de reducciones adicionales será más notable y todo comenzará a suceder más rápido.
, , , , , : «, !». , g c ₀ ' , q, , g _high q, g _high mod q . , . – , , .

c ₀ ' mod q. c ₀ g _high , q, , g q. , . , , . , 32- , .

, 32- , , , . , . 32 , , - . , , 32, , , , .

, , , . , q 1, , q 0, , g _high q , , .

. , . , . , , 1-2 . , , Ethernet.
, . . , 7 . , , -, , ?

: ?

: , , , , , . , .

, , 7 , , 7 . 7 g, 7 g + 1, g + 2 7 g + 400. g, g, , 7 400, ?



: , , ?

: , , , — (c ₀ ') ^d . . , , , mod p. , , . , g, 1, 2, 3, , .

, , – 100…00. , mod p, , mod p . « », , (c ₀ ') ^d , . ?

: , ?

: - , q. , q, , , .

: c ₀ '?

: c ₀ ', c, c ₀ ' R mod n.



, «» , c ₀ = mod q, c ₀ = ((c ₀ ' R ^-1 ) mod n) mod q. R, R. c ₀ ', (c ₀ ') ^d mod q. , , , , R. , R = 2 ⁵¹² . , .

: mod p ?

: , , ? , ! , .


.

Gracias por quedarte con nosotros. ¿Te gustan nuestros artículos? ¿Quieres ver más materiales interesantes? Apóyenos haciendo un pedido o recomendándolo a sus amigos, un descuento del 30% para los usuarios de Habr en un análogo único de servidores de nivel de entrada que inventamos para usted: toda la verdad sobre VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de $ 20 o cómo dividir el servidor? (las opciones están disponibles con RAID1 y RAID10, hasta 24 núcleos y hasta 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 veces más barato? Solo tenemos 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV desde $ 249 en los Países Bajos y los EE. UU. Lea sobre Cómo construir un edificio de infraestructura. clase utilizando servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?