🛁 🤶🏾 👩‍👩‍👧 Julia y el movimiento de una partícula cargada en un campo electromagnético ⚖️ 🍁 📚

Fortalecemos las habilidades para resolver y visualizar ecuaciones diferenciales usando una de las ecuaciones evolutivas más comunes como ejemplo, recuerda el viejo Scilab y trata de entender si lo necesitamos ... Debajo de la imagen cortada (kilobytes por setecientos)

Asegúrese de que el software esté actualizado

julia>] (v1.0) pkg>update #   (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Repasemos las guías pasadas

y proceder a la declaración del problema

El movimiento de partículas cargadas en un campo electromagnético.

En una partícula cargada con una carga $q$ moviéndose en EMF con velocidad $u$ la fuerza de Lorentz actúa: $\ vec {F} _L = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$ . Esta fórmula es válida con varias simplificaciones. Al descuidar las correcciones a la teoría de la relatividad, consideramos que la masa de partículas es constante, por lo que la ecuación de movimiento tiene la forma: $\ frac {d} {dt} (m \ vec {u}) = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$

Dirijamos el eje Y a lo largo del campo eléctrico, el eje Z a lo largo del campo magnético, y supongamos por simplicidad que la velocidad de partícula inicial se encuentra en el plano XY. En este caso, toda la trayectoria de la partícula también estará en este plano. Las ecuaciones de movimiento tomarán la forma:

\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right. $

$\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right. $$

Inconmensurable: $x ^ * = \ frac {x} {\ lambda}, \, y ^ * = \ frac {y} {\ lambda}, \, \ tau = \ frac {ct} {\ lambda}, \, B ^ * = \ frac {Bmc} {q \ lambda}, \, E ^ * = \ frac {Emc ^ 2} {q \ lambda}$ . Los asteriscos indican cantidades dimensionales, y $\ lambda$ - el tamaño característico del sistema físico considerado. Obtenemos un sistema adimensional de ecuaciones de movimiento de una partícula cargada en un campo magnético:

\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right. $

$\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right. $$

Bajemos el orden:

\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matriz} \ right. $

$\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matriz} \ right. $$

Como configuración inicial del modelo, elegimos: $B = 2$ T $E = 5 \ cdot 10 ^ 4$ V / m $v_0 = 7 \ cdot 10 ^ 4$ m / s Para una solución numérica, usamos el paquete DifferentialEquations :

Código y Gráficos

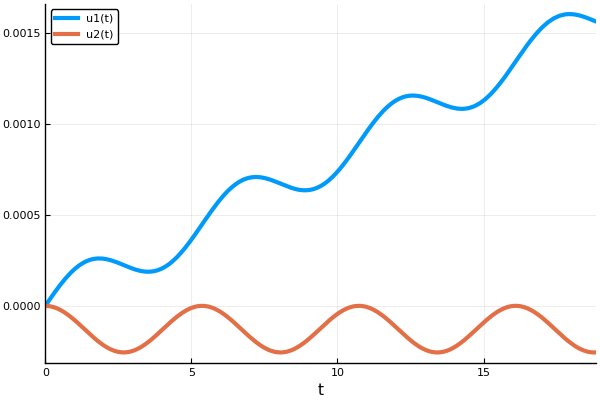
 using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)

Aquí usamos el método Euler, para el cual se especifica el número de pasos. Además, no toda la solución del sistema se guarda en la matriz de respuestas, sino solo 1 y 2 índices, es decir, las coordenadas de la X y el reproductor (no necesitamos velocidades).

 X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

Comprueba el resultado. Introducimos una nueva variable en lugar de x $\ tilde {x} = x-ut$ . Por lo tanto, se realiza una transición a un nuevo sistema de coordenadas que se mueve con relación al original con una velocidad u en la dirección del eje X :

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matriz} \ derecha. $

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matriz} \ derecha. $$

Si eliges $u = E / B$ y denotar $\ omega = qB / m$ , entonces el sistema se simplificará:

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matriz} \ derecha. $

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matriz} \ derecha. $$

El campo eléctrico ha desaparecido de las últimas igualdades, y son las ecuaciones de movimiento de una partícula bajo la influencia de un campo magnético uniforme. Por lo tanto, la partícula en el nuevo sistema de coordenadas (x, y) debe moverse en un círculo. Dado que este nuevo sistema de coordenadas se mueve con respecto al original con rapidez $u = E / B$ , entonces el movimiento de partículas resultante consistirá en un movimiento uniforme a lo largo del eje X y rotación alrededor del círculo en el plano XY . Como saben, la trayectoria que ocurre cuando se suman estos dos movimientos es generalmente un trocoide . En particular, si la velocidad inicial es cero, se realiza el caso más simple de movimiento de este tipo, a lo largo del cicloide .
Asegurémonos de que la velocidad de deriva sea realmente igual a E / V. Para hacer esto:

estropearemos la matriz de respuesta estableciendo un valor deliberadamente más bajo en lugar del primer elemento (máximo)
encontramos el número del elemento máximo en la segunda columna de la matriz de respuesta, que se retrasa por ordenadas
calculamos la velocidad de deriva adimensional dividiendo el valor máximo de abscisa por el valor de tiempo correspondiente

 Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]

Fuera: 8.334546850446588e-5

 B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B

Fuera: 8.33333333333333332e-5
¡Hasta séptimo orden!
Por conveniencia, definimos una función que toma los parámetros del modelo y la firma del gráfico, que también servirá como el nombre del archivo png creado en la carpeta del proyecto (funciona en Juno / Atom y Jupyter). A diferencia de Gadfly , donde los gráficos fueron creados en capas y luego mostrados por la función plot () , en Plots, para crear diferentes gráficos en un cuadro, el primero de ellos es creado por la función plot () , y los siguientes se agregan usando plot! () . Los nombres de las funciones que cambian los objetos aceptados en Julia son habituales para terminar con un signo de exclamación.

 function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end

A velocidad inicial cero, como se esperaba, obtenemos un cicloide :

 plot() plotter("Zero start velocity", 2, 4e4, 7e4)

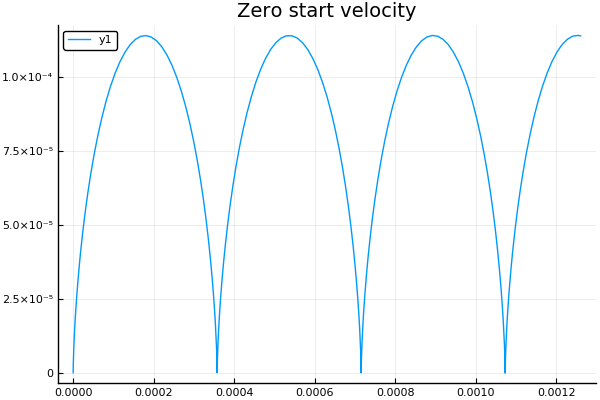
Obtenemos la trayectoria de la partícula cuando la inducción, la intensidad y cuando cambia el signo de carga. Permítame recordarle que un punto significa la ejecución secuencial de una función con todos los elementos de la matriz.

Escondido

 plot() plotter.("B   ", 0, [3e4 4e4 5e4 6e4] )

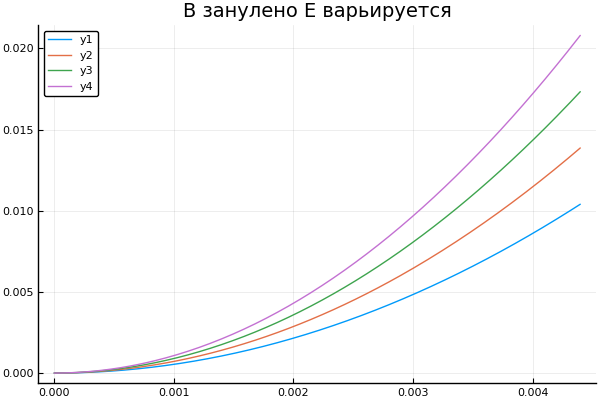
 plot() plotter.("E  B ", [1 2 3 4], 0 )

 q = -1.6e-19 # C plot() plotter.(" ")

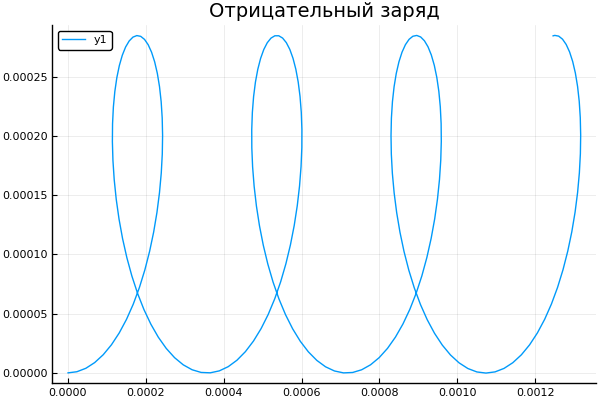
Y veamos cómo el cambio en la velocidad inicial afecta la trayectoria de la partícula:

 plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )

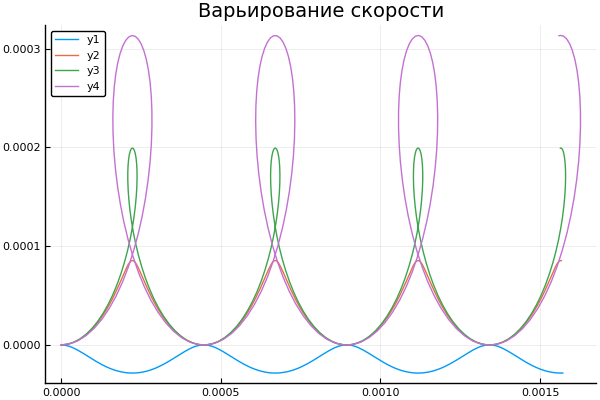
Un poco sobre Scilab

En Habré ya hay suficiente información sobre Silab, por ejemplo 1 , 2 , y aquí sobre Octave, por lo tanto, nos limitaremos a enlaces a Wikipedia y a la página de inicio .

Por mi cuenta, agregaré sobre la presencia de una interfaz conveniente con casillas de verificación, botones y gráficos, y una herramienta de modelado visual Xcos bastante interesante. Este último puede usarse, por ejemplo, para simular una señal en ingeniería eléctrica:

Spoiler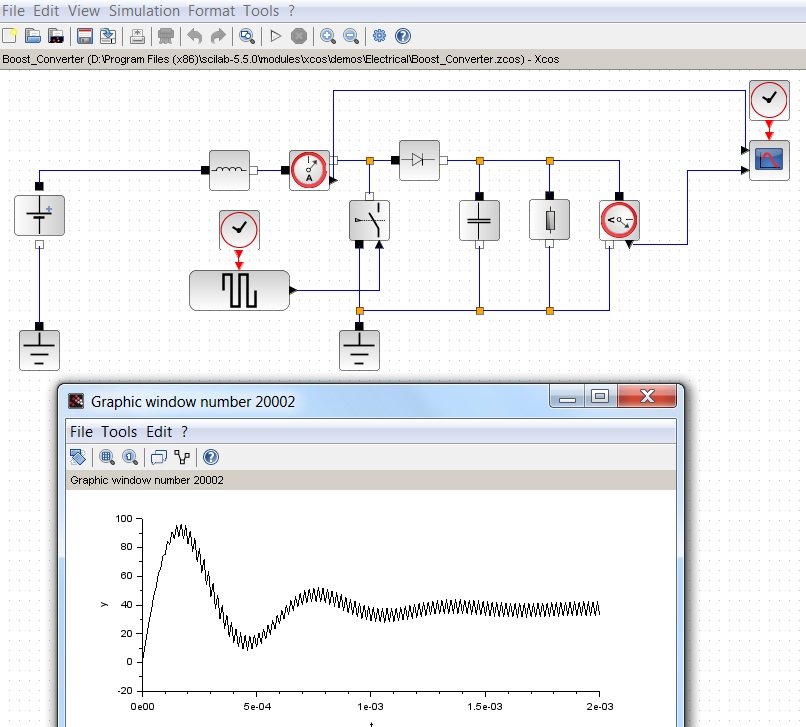

Y aquí hay una guía muy conveniente:

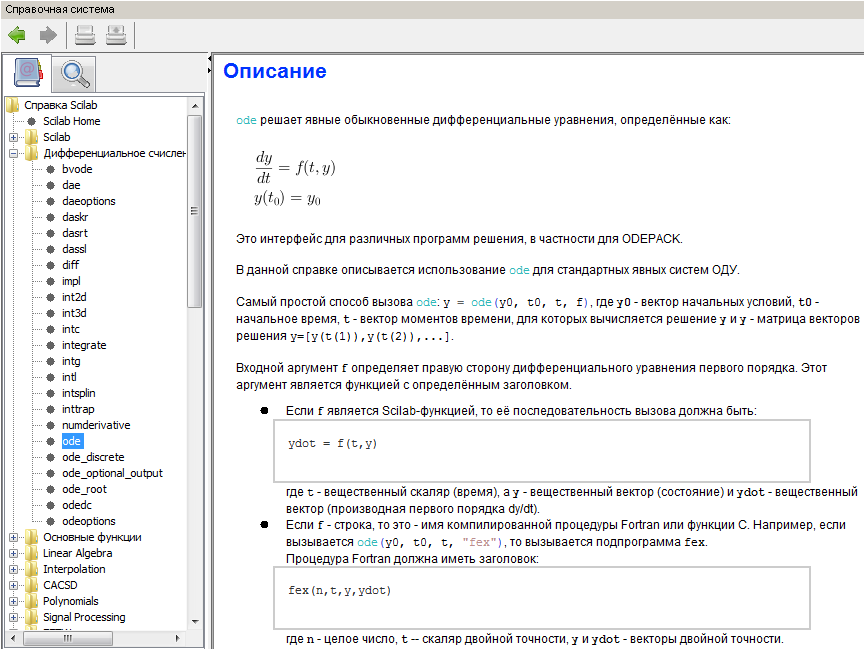
En realidad, nuestra tarea también se puede resolver en Scilab:

Código y fotos

 clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle ("   ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)//    plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');//       xs2jpg(1,'graf2');// ,  -

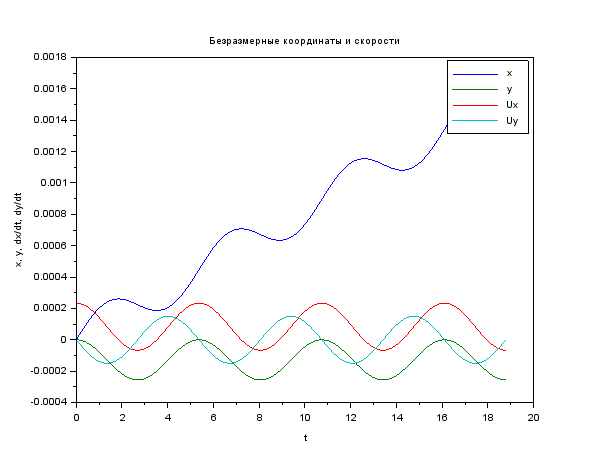
Aquí hay información sobre la función para resolver las diferencias de oda. En principio, la pregunta plantea

¿Por qué necesitamos a Julia?

... si hay cosas tan maravillosas como Scilab, Octave y Numpy, Scipy?
Sobre los dos últimos no lo diré, no lo he probado. Y en general la pregunta es complicada, así que echemos un vistazo rápido:

Scilab
En un disco duro tomará un poco más de 500 MB, se iniciará rápidamente e inmediatamente habrá cálculos diferenciales disponibles, gráficos y todo lo demás. Bueno para principiantes: una excelente guía (principalmente localizada), hay muchos libros en ruso. Ya se han dicho errores internos aquí y aquí , y dado que el producto es muy específico, la comunidad es lenta y los módulos adicionales son muy escasos.

Julia
A medida que se agregan paquetes (especialmente cualquier python-a la Jupyter y Mathplotlib), crece de 376 MB a un poco más de seis gigabytes. Tampoco ahorra RAM: al comienzo de 132 MB y después de planear los horarios en Júpiter, alcanzará tranquilamente 1 GB. Si trabaja en Juno , entonces todo es casi como en Scilab : puede ejecutar el código inmediatamente en el intérprete, puede imprimir en el bloc de notas incorporado y guardarlo como un archivo, hay un navegador variable, un registro de comandos y ayuda en línea. Personalmente, estoy indignado por la falta de clear () , es decir, ejecuté el código, luego comencé a corregirlo y cambiarle el nombre, y las antiguas variables permanecieron (no hay un navegador de variables en Júpiter).

Pero todo esto no es crítico. Scilab es bastante adecuado para la primera pareja, hacer una frente, un cursor o calcular algo intermedio es una herramienta muy improvisada. Aunque también hay soporte para computación paralela y llamadas a funciones sishn / Fortran, para lo cual no se puede usar en serio. Las grandes matrices lo aterrorizan, para establecer las multidimensionales, debe lidiar con todo tipo de oscurantismo , y los cálculos más allá del alcance de las tareas clásicas bien pueden dejar todo junto con el sistema operativo.

Y después de todos estos dolores y decepciones, también puedes cambiar a Julia para rastrillar aquí. Continuaremos estudiando, el beneficio de la comunidad es muy receptivo, los problemas se resuelven rápidamente y Julia tiene muchas más características interesantes que convertirán el proceso de aprendizaje en un viaje emocionante.

Julia y el movimiento de una partícula cargada en un campo electromagnético

El movimiento de partículas cargadas en un campo electromagnético.

Un poco sobre Scilab

¿Por qué necesitamos a Julia?

More articles: