capítulos anteriores

Curvas de aprendizaje

28 Diagnóstico de sesgos y dispersión: curvas de aprendizaje

Examinamos varios enfoques para la separación de errores en sesgo y dispersión evitables. Hicimos esto evaluando la proporción óptima de errores, calculando errores en la muestra de entrenamiento del algoritmo y en la muestra de validación. Analicemos un enfoque más informativo: gráficos de curvas de aprendizaje.
Los gráficos de las curvas de aprendizaje son las dependencias de la cuota de error en el número de ejemplos de la muestra de entrenamiento.

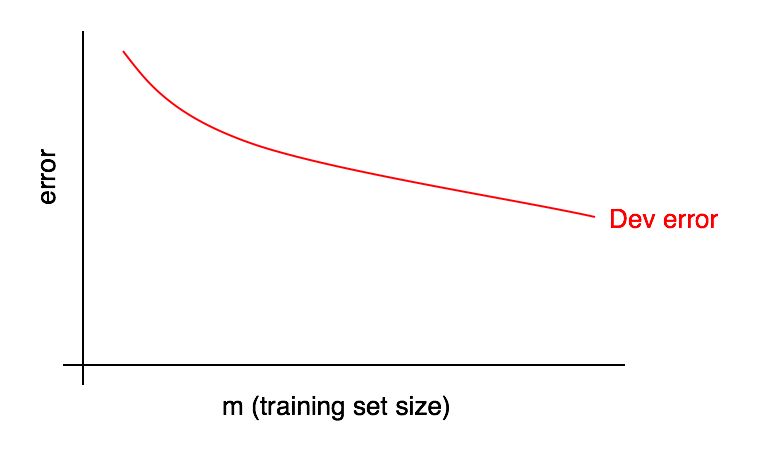
A medida que aumenta el tamaño de la muestra de entrenamiento, el error en la muestra de validación debería disminuir.
A menudo nos enfocaremos en algunos "errores deseados" que esperamos lleguen a nuestro algoritmo. Por ejemplo:

• Si esperamos alcanzar un nivel de calidad accesible para el hombre, la proporción de errores humanos debería convertirse en la "proporción de errores deseada"
• Si el algoritmo de aprendizaje se utiliza en algún producto (como un proveedor de imágenes de gato), podemos comprender qué nivel de calidad necesita alcanzar para que los usuarios obtengan el mayor beneficio
• Si ha estado trabajando en una aplicación importante durante mucho tiempo, puede tener una comprensión razonable de los progresos que puede hacer en el próximo trimestre / año.

Agregue el nivel de calidad deseado a nuestra curva de aprendizaje:

Puede extrapolar visualmente la curva de error roja en la muestra de validación y asumir qué tan cerca podría llegar al nivel de calidad deseado agregando más datos. En el ejemplo que se muestra en la imagen, parece probable que duplicar el tamaño de la muestra de entrenamiento alcanzará el nivel de calidad deseado.
Sin embargo, si la curva de la fracción del error de la muestra de validación ha alcanzado una meseta (es decir, se ha convertido en una línea recta paralela al eje de la abscisa), indica inmediatamente que agregar datos adicionales no ayudará a lograr el objetivo:

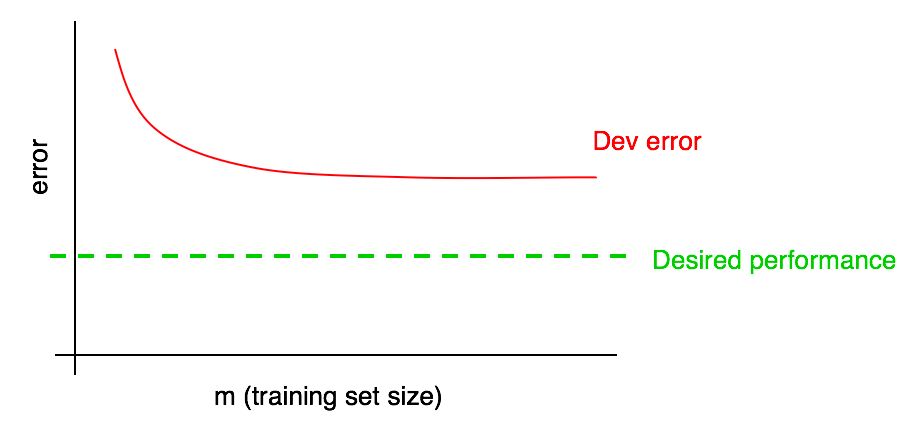
Una mirada a la curva de aprendizaje puede ayudarlo a evitar perder meses recolectando el doble de datos de entrenamiento solo para darse cuenta de que agregarlo no ayuda.
Uno de los inconvenientes de este enfoque es que si solo observa la curva de error en la muestra de validación, puede ser difícil extrapolar y predecir con precisión cómo se comportará la curva roja si agrega más datos. Por lo tanto, hay otro gráfico adicional que puede ayudar a evaluar el impacto de los datos de capacitación adicionales en la proporción de errores: un error de aprendizaje.

29 Horario de errores de aprendizaje

Los errores en las muestras de validación (y prueba) deberían disminuir a medida que aumenta la muestra de entrenamiento. Pero en la muestra de entrenamiento, el error al agregar datos generalmente crece.

Vamos a ilustrar este efecto con un ejemplo. Suponga que su muestra de entrenamiento consta de solo 2 ejemplos: una imagen con gatos y otra sin gatos. En este caso, el algoritmo de aprendizaje puede recordar fácilmente ambos ejemplos de la muestra de entrenamiento y mostrar un 0% de error en la muestra de entrenamiento. Incluso si ambos ejemplos de entrenamiento están etiquetados incorrectamente, el algoritmo recordará fácilmente sus clases.

Ahora imagine que su conjunto de entrenamiento consta de 100 ejemplos. Suponga que cierto número de ejemplos se clasifican incorrectamente, o es imposible establecer una clase en algunos ejemplos, por ejemplo, en imágenes borrosas, cuando incluso una persona no puede determinar si un gato está presente en la imagen o no. Suponga que el algoritmo de aprendizaje todavía "recuerda" la mayoría de los ejemplos de muestra de capacitación, pero ahora es más difícil obtener una precisión del 100%. Aumentando la muestra de entrenamiento de 2 a 100 ejemplos, encontrará que la precisión del algoritmo en la muestra de entrenamiento disminuirá gradualmente.

Al final, supongamos que su conjunto de entrenamiento consta de 10,000 ejemplos. En este caso, se vuelve cada vez más difícil para el algoritmo clasificar idealmente todos los ejemplos, especialmente si el conjunto de entrenamiento contiene imágenes borrosas y errores de clasificación. Por lo tanto, su algoritmo funcionará peor en tal muestra de entrenamiento.

Agreguemos un gráfico de error de aprendizaje a los anteriores.

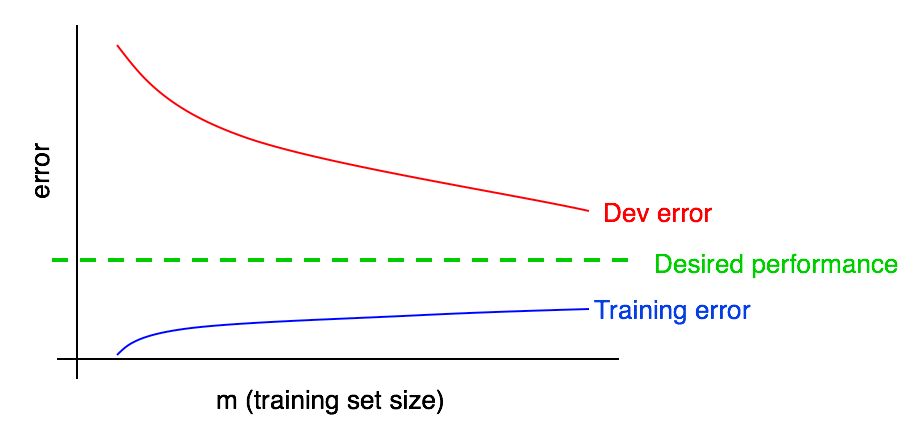
Puede ver que la curva azul "Errores de aprendizaje" crece con un aumento en la muestra de entrenamiento. Además, un algoritmo de aprendizaje generalmente muestra mejor calidad en una muestra de entrenamiento que en una de validación; por lo tanto, la curva de error roja en la muestra de validación se encuentra estrictamente por encima de la curva de error azul en la muestra de entrenamiento.

A continuación, analicemos cómo interpretar estos gráficos.

continuación