• Programa educativo sobre teoría de la probabilidad (artículo introductorio, opcional)
  
• Introducción a los sistemas lineales de ecuaciones.
  
• Métodos de elementos finitos
  
• Minimización de formas cuadráticas y ejemplos de problemas de MCO
  
• De mínimos cuadrados a redes neuronales
  

Entonces, otro artículo del ciclo de "matemáticas en los dedos ". Hoy continuamos la discusión sobre los métodos de mínimos cuadrados, pero esta vez desde el punto de vista del programador. Este es otro artículo de la serie, pero se distingue, ya que generalmente no requiere ningún conocimiento de las matemáticas. El artículo fue concebido como una introducción a la teoría, por lo que a partir de habilidades básicas requiere la capacidad de encender una computadora y escribir cinco líneas de código. Por supuesto, no me detendré en este artículo, y en un futuro cercano publicaré una secuela. Si puedo encontrar suficiente tiempo, escribiré un libro de este material. El público objetivo son los programadores, por lo que Habr es el lugar adecuado para entrar. En general, no me gusta escribir fórmulas, y realmente me gusta aprender de los ejemplos, me parece que es muy importante, no solo mirar los garabatos en el tablero de la escuela, sino probar todo en el diente.

Entonces comencemos. Imaginemos que tengo una superficie triangulada con un escaneo de mi cara (en la imagen de la izquierda). ¿Qué necesito hacer para mejorar las características, convirtiendo esta superficie en una máscara grotesca?



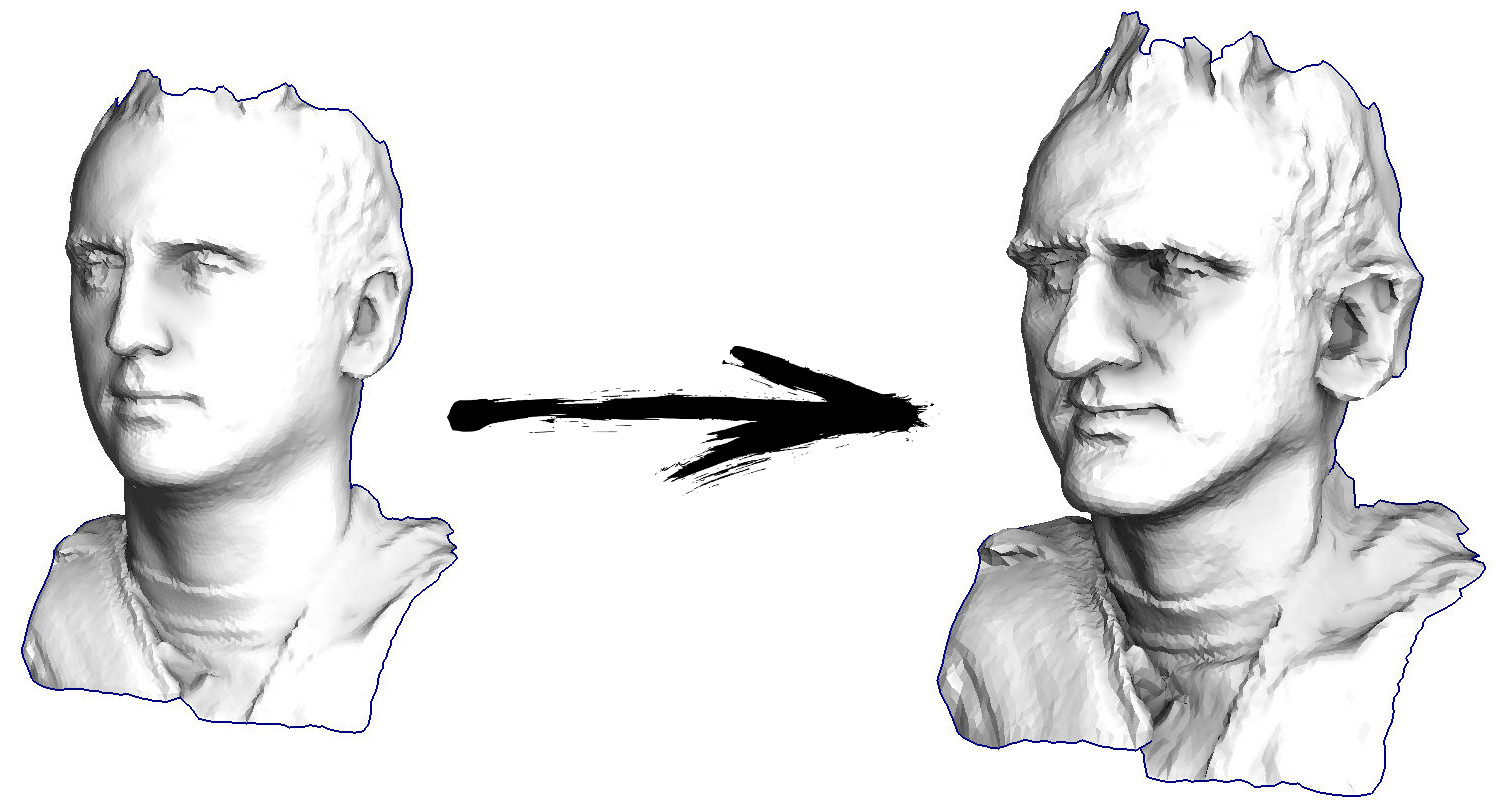
En este caso particular, resuelvo una ecuación diferencial elíptica llamada Simeon Demi Poisson . Compañeros programadores, juguemos un juego: ¿adivina cuántas líneas hay en el código C ++ que lo decide? No se puede llamar a las bibliotecas de terceros, solo tenemos un compilador desnudo a nuestra disposición. La respuesta está debajo del corte.

De hecho, veinte líneas de código son suficientes para un solucionador. Si cuenta con todo, todo, incluido el analizador del archivo de modelo 3D, manténgase dentro de doscientas líneas, solo escupe.

Ejemplo 1: suavizado de datos

Hablemos de cómo funciona. Comencemos desde lejos, imagine que tenemos una matriz regular f, por ejemplo, de 32 elementos, inicializados de la siguiente manera:



Y luego realizaremos el siguiente procedimiento mil veces: para cada celda f [i] escribimos el valor promedio de las celdas vecinas: f [i] = (f [i-1] + f [i + 1]) / 2. Para hacerlo más claro, aquí está el código completo:

import matplotlib.pyplot as plt f = [0.] * 32 f[0] = f[-1] = 1. f[18] = 2. plt.plot(f, drawstyle='steps-mid') for iter in range(1000): f[0] = f[1] for i in range(1, len(f)-1): f[i] = (f[i-1]+f[i+1])/2. f[-1] = f[-2] plt.plot(f, drawstyle='steps-mid') plt.show() 

Cada iteración suavizará los datos de nuestra matriz, y después de mil iteraciones obtendremos un valor constante en todas las celdas. Aquí hay una animación de las primeras ciento cincuenta iteraciones:



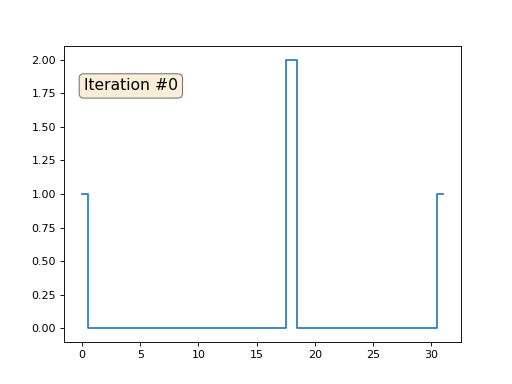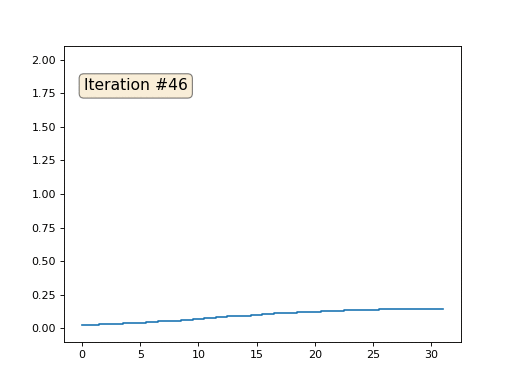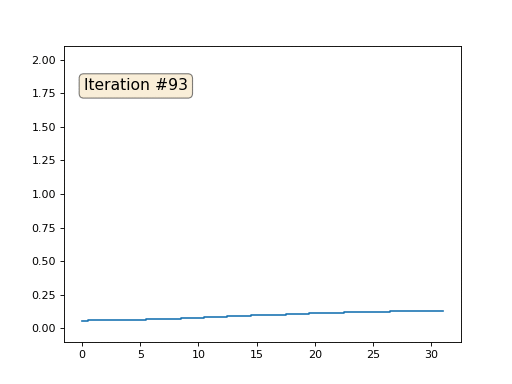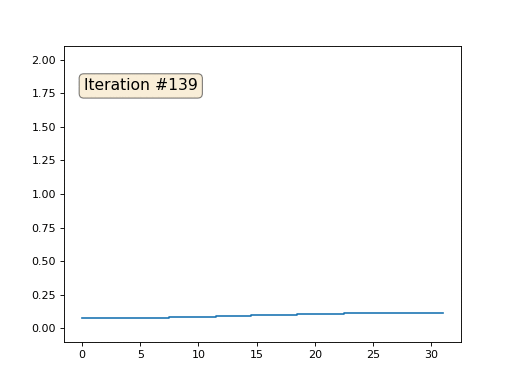
Si no está claro por qué ocurre el suavizado, deténgase ahora mismo, tome un bolígrafo e intente dibujar ejemplos, de lo contrario, no tiene sentido seguir leyendo. La superficie triangulada es esencialmente la misma que este ejemplo. Imagine que para cada vértice encontraremos sus vecinos, calcularemos su centro de masa y moveremos nuestro vértice a este centro de masa, y así diez veces. El resultado será así:



Por supuesto, si no se detiene en diez iteraciones, luego de un tiempo, toda la superficie se comprimirá en un punto exactamente de la misma manera que en el ejemplo anterior, toda la matriz se llenó con el mismo valor.

Ejemplo 2: características de mejora / atenuación

El código completo está disponible en el github , pero aquí daré la parte más importante, omitiendo solo la lectura y escritura de modelos 3D. Entonces, el modelo triangulado para mí está representado por dos matrices: verts y caras. La matriz de verts es solo un conjunto de puntos tridimensionales, son los vértices de la malla poligonal. La matriz de caras es un conjunto de triángulos (el número de triángulos es igual a faces.size ()), para cada triángulo, los índices de la matriz de vértices se almacenan en la matriz. El formato de datos y el trabajo con ellos lo describí en detalle en mi curso de conferencias sobre gráficos por computadora. También hay una tercera matriz, que relato de las dos primeras (más precisamente, solo de la matriz de caras): vvadj. Esta es una matriz que para cada vértice (el primer índice de una matriz bidimensional) almacena los índices de sus vecinos (segundo índice).

 std::vector<Vec3f> verts; std::vector<std::vector<int> > faces; std::vector<std::vector<int> > vvadj; 

Lo primero que hago es que para cada vértice de mi superficie considero el vector de curvatura. Vamos a ilustrar: para el vértice actual v, itero sobre todos sus vecinos n1-n4; entonces cuento su centro de masa b = (n1 + n2 + n3 + n4) / 4. Bueno, el vector de curvatura final se puede calcular como c = vb, no se parece en nada a las diferencias finitas ordinarias para la segunda derivada .



Directamente en el código, se ve así:

  std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0)); for (int i=0; i<(int)verts.size(); i++) { for (int j=0; j<(int)vvadj[i].size(); j++) { curvature[i] = curvature[i] - verts[vvadj[i][j]]; } curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size(); } 

Bueno, entonces hacemos lo siguiente muchas veces (ver la imagen anterior): movemos el vértice v a v: = b + const * c. Tenga en cuenta que si la constante es igual a uno, ¡nuestro vértice no se moverá a ninguna parte! Si la constante es cero, entonces el vértice se reemplaza por el centro de masa de los vértices vecinos, lo que suavizará nuestra superficie. Si la constante es mayor que la unidad (la imagen del título se realizó con const = 2.1), entonces el vértice se desplazará en la dirección del vector de curvatura de la superficie, fortaleciendo los detalles. Así es como se ve en el código:

  for (int it=0; it<100; it++) { for (int i=0; i<(int)verts.size(); i++) { Vec3f bary(0,0,0); for (int j=0; j<(int)vvadj[i].size(); j++) { bary = bary + verts[vvadj[i][j]]; } bary = bary / (float)vvadj[i].size(); verts[i] = bary + curvature[i]*2.1; // play with the coeff here } } 

Por cierto, si es menor que la unidad, entonces los detalles se debilitarán por el contrario (const = 0.5), pero esto no será equivalente a un simple suavizado, el "contraste de la imagen" permanecerá:



Tenga en cuenta que mi código genera un archivo de modelo 3D en formato Wavefront .obj , lo rendericé en un programa de terceros. Puede ver el modelo resultante, por ejemplo, en el visor en línea . Si está interesado en los métodos de representación, en lugar de generar el modelo, lea mi curso sobre gráficos por computadora .

Ejemplo 3: agregar restricciones

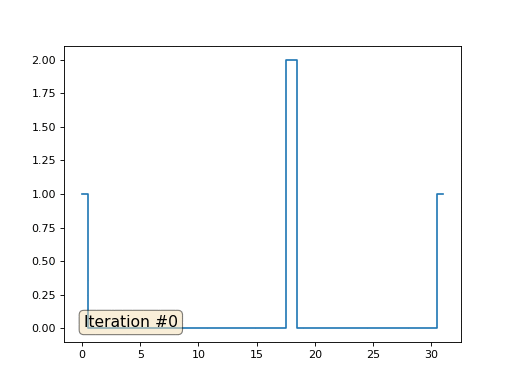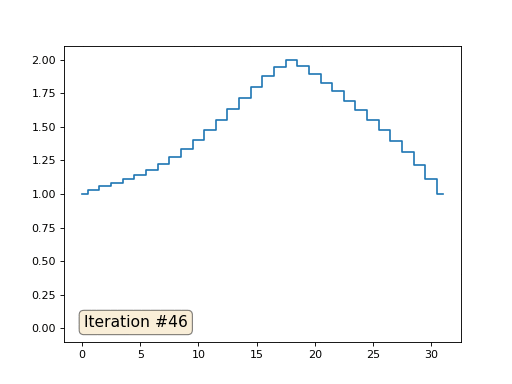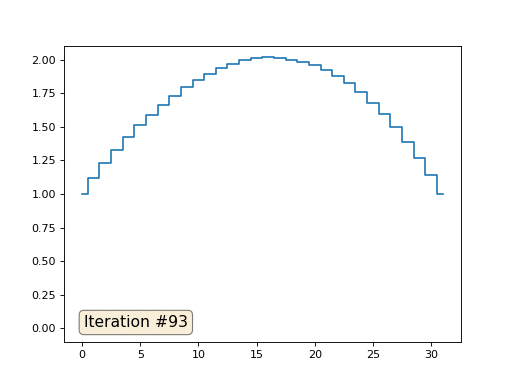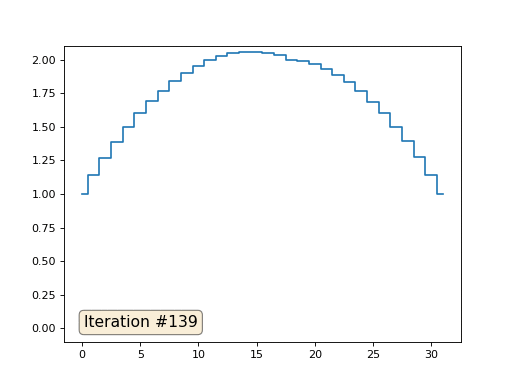
Volvamos al primer ejemplo y hagamos exactamente lo mismo, pero no reescribiremos los elementos de la matriz con los números 0, 18 y 31:

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. plt.plot(x, drawstyle='steps-mid') plt.show() 

Inicialicé el resto, elementos "libres" de la matriz con ceros, y todavía los reemplazo iterativamente con el valor promedio de los elementos vecinos. Así es como se ve la evolución de la matriz en las primeras ciento cincuenta iteraciones:



Es bastante obvio que esta vez la solución convergerá no a un elemento constante que llene la matriz, sino a dos rampas lineales. Por cierto, ¿es realmente obvio para todos? Si no, entonces experimente con este código, específicamente doy ejemplos con un código muy corto para que pueda comprender completamente lo que está sucediendo.

Digresión lírica: solución numérica de sistemas de ecuaciones lineales.

Se nos dará el sistema habitual de ecuaciones lineales:



Se puede reescribir, dejando en cada una de las ecuaciones en un lado del signo igual x_i:



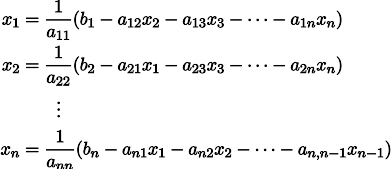
Se nos dará un vector arbitrario aproximando la solución de un sistema de ecuaciones (por ejemplo, cero).

Luego, pegándolo en el lado derecho de nuestro sistema, podemos obtener un vector de aproximación de solución actualizado .

Para hacerlo más claro, x1 se obtiene de x0 de la siguiente manera:



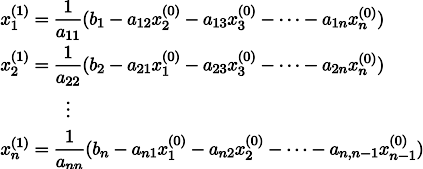
Repitiendo el proceso k veces, la solución será aproximada por el vector

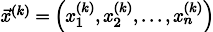
Por si acaso, escriba una fórmula de recursión:



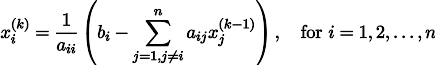
Bajo algunos supuestos acerca de los coeficientes del sistema (por ejemplo, es obvio que los elementos diagonales no deberían ser cero, porque los dividimos), este procedimiento converge a la solución verdadera. Esta gimnasia es conocida en la literatura como el método Jacobi . Por supuesto, hay otros métodos para resolver numéricamente sistemas de ecuaciones lineales, y otros mucho más potentes, por ejemplo, el método de gradiente conjugado , pero, quizás, el método de Jacobi es uno de los más simples.

Ejemplo 3 nuevamente, pero por otro lado

Y ahora echemos un vistazo más de cerca al bucle principal del Ejemplo 3:

 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. 

¡Comencé con un vector inicial x, y lo actualicé mil veces, y el procedimiento de actualización es sospechosamente similar al método de Jacobi! Escribamos este sistema de ecuaciones explícitamente:



Tómese un poco de tiempo, asegúrese de que cada iteración en mi código de Python sea estrictamente una actualización del método Jacobi para este sistema de ecuaciones. Los valores x [0], x [18] yx [31] son ​​fijos para mí, respectivamente, no están incluidos en el conjunto de variables, por lo tanto, se transfieren al lado derecho.

En total, todas las ecuaciones en nuestro sistema se ven como - x [i-1] + 2 x [i] - x [i + 1] = 0. Esta expresión no es más que diferencias finitas ordinarias para la segunda derivada . Es decir, nuestro sistema de ecuaciones simplemente prescribe que la segunda derivada debe ser igual a cero en todas partes (bueno, excepto en el punto x [18]). ¿Recuerdas que dije que es obvio que las iteraciones deberían converger en rampas lineales? Esa es precisamente la razón por la cual la derivada lineal de la segunda derivada es cero.

¿Sabes que acabamos de resolver el problema de Dirichlet para la ecuación de Laplace ?

Por cierto, un lector atento debería haber notado que, estrictamente hablando, en mi código, los sistemas de ecuaciones lineales se resuelven no por el método de Jacobi, sino por el método de Gauss-Seidel , que es una especie de optimización del método de Jacobi:

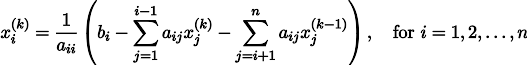
Ejemplo 4: ecuación de Poisson

Y cambiemos el tercer ejemplo solo un poco: cada celda se coloca no solo en el centro de masa de las celdas vecinas, sino en el centro de masa más alguna constante (arbitraria):

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1] +11./32**2 )/2. plt.plot(x, drawstyle='steps-mid') plt.show() 

En el ejemplo anterior, encontramos que colocar en el centro de masa es la discretización del operador de Laplace (en nuestro caso, la segunda derivada). Es decir, ahora estamos resolviendo un sistema de ecuaciones que dice que nuestra señal debe tener una segunda derivada constante. La segunda derivada es la curvatura de la superficie; por lo tanto, una función cuadrática por partes debería ser la solución a nuestro sistema. Veamos el muestreo en 32 muestras:



Con una longitud de matriz de 32 elementos, nuestro sistema converge en una solución en un par de cientos de iteraciones. Pero, ¿y si probamos una matriz de 128 elementos? Aquí todo es mucho más triste, el número de iteraciones ya debe calcularse en miles:



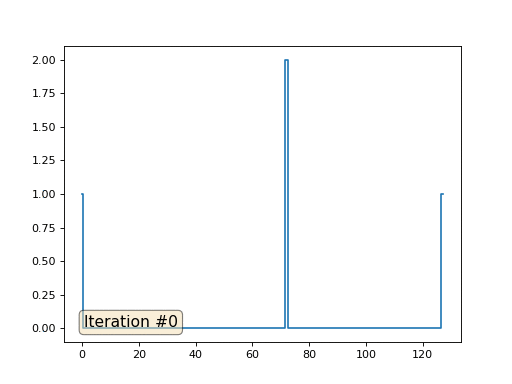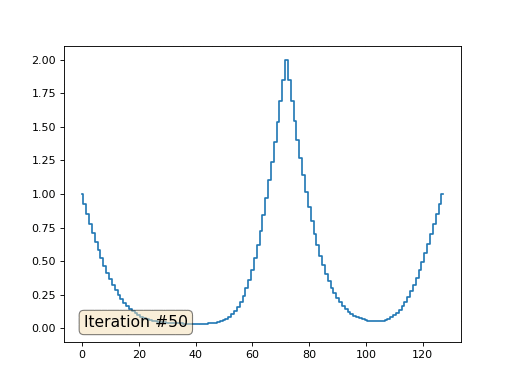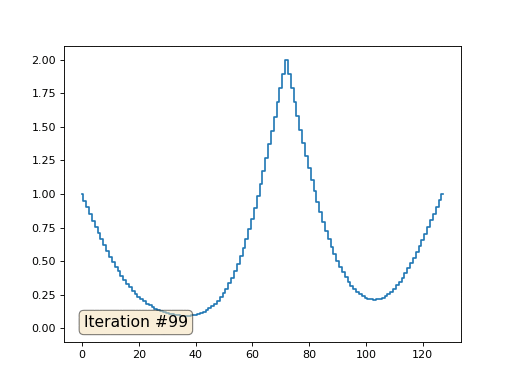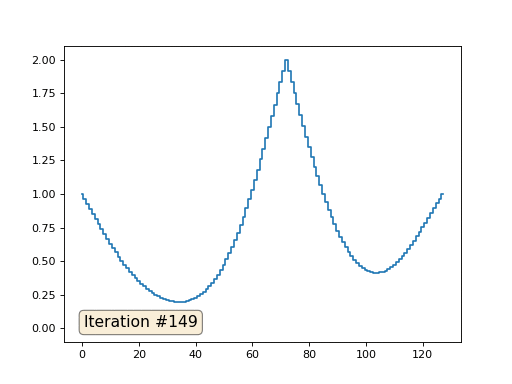
El método de Gauss-Seidel es extremadamente simple de programar, pero no aplicable para grandes sistemas de ecuaciones. Puede intentar acelerarlo utilizando, por ejemplo, métodos de cuadrícula múltiple . En palabras, esto puede sonar engorroso, pero la idea es extremadamente primitiva: si queremos una solución con una resolución de mil elementos, primero podemos resolver con diez elementos, obtener una aproximación aproximada, luego duplicar la resolución, resolverla nuevamente, y así sucesivamente, hasta que alcancemos Resultado deseado. En la práctica, se ve así:



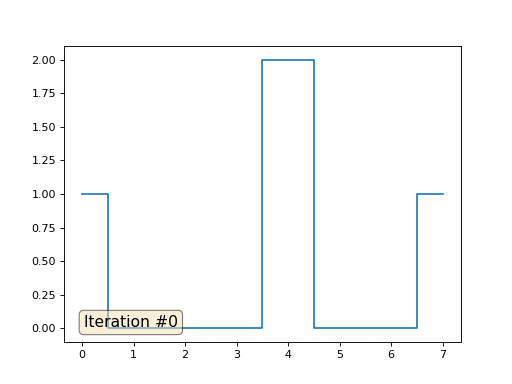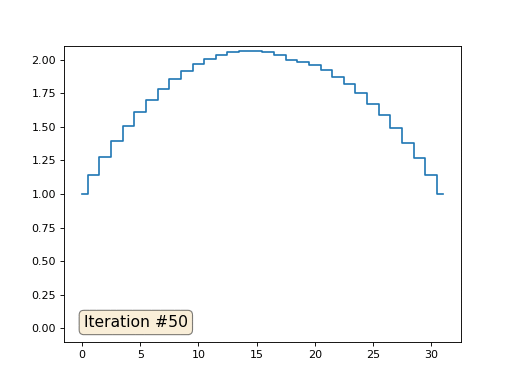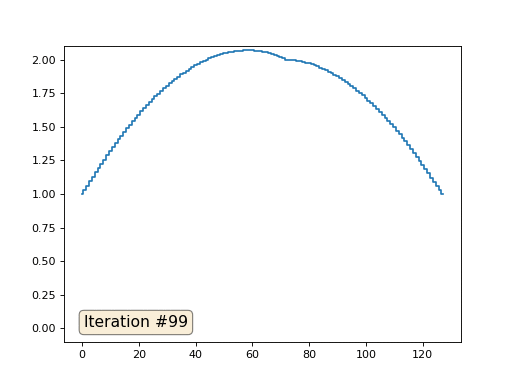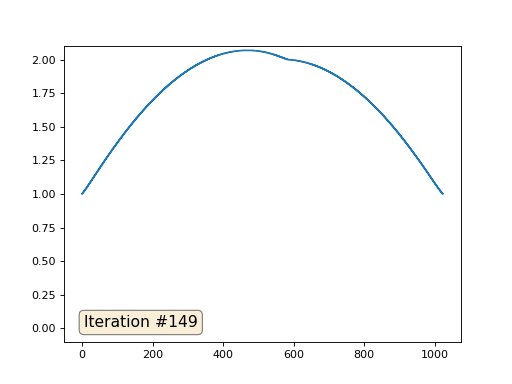
Y no puede presumir, y usar solucionadores reales de sistemas de ecuaciones. Así que resuelvo el mismo ejemplo construyendo la matriz A y la columna b, y luego resolviendo la ecuación matricial Ax = b:

 import numpy as np import matplotlib.pyplot as plt n=1000 x = [0.] * n x[0] = x[-1] = 1. m = n*57//100 x[m] = 2. A = np.matrix(np.zeros((n, n))) for i in range(1,n-2): A[i, i-1] = -1. A[i, i] = 2. A[i, i+1] = -1. A = A[1:-2,1:-2] A[m-2,m-1] = 0 A[m-1,m-2] = 0 b = np.matrix(np.zeros((n-3, 1))) b[0,0] = x[0] b[m-2,0] = x[m] b[m-1,0] = x[m] b[-1,0] = x[-1] for i in range(n-3): b[i,0] += 11./n**2 x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0]) x2.insert(0, x[0]) x2.insert(m, x[m]) x2.append(x[-1]) plt.plot(x2, drawstyle='steps-mid') plt.show() 

Y aquí está el resultado del trabajo de este programa, tenga en cuenta que la solución resultó al instante:



Por lo tanto, de hecho, nuestra función es cuadrática por partes (la segunda derivada es constante). En el primer ejemplo, establecemos la segunda segunda derivada en cero, la tercera no es cero, pero igual en todas partes. ¿Y qué había en el segundo ejemplo? Resolvimos la ecuación discreta de Poisson especificando la curvatura de la superficie. Permítame recordarle lo que sucedió: calculamos la curvatura de la superficie entrante. Si resolvemos el problema de Poisson al establecer la curvatura de la superficie en la salida igual a la curvatura de la superficie en la entrada (const = 1), entonces nada cambiará. El fortalecimiento de las características faciales ocurre cuando simplemente aumentamos la curvatura (const = 2.1). Y si const <1, entonces la curvatura de la superficie resultante disminuye.

Actualización: otro juguete como tarea

Desarrollando la idea sugerida por SquareRootOfZero , juegue con este código:



Este es el resultado predeterminado, Lenin rojo es el dato inicial, la curva azul es su evolución, en el infinito el resultado converge a un punto:



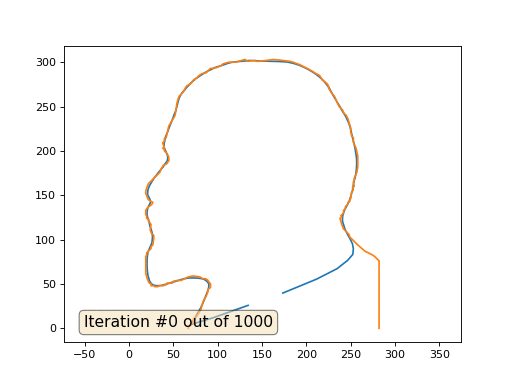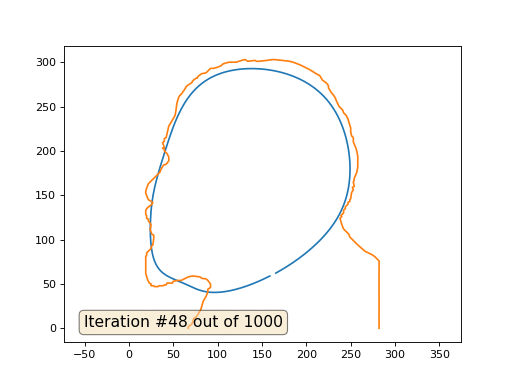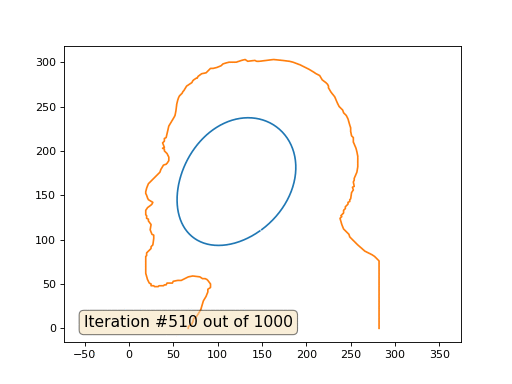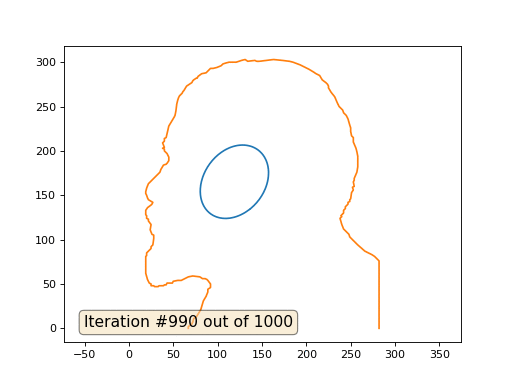
Y aquí está el resultado con el coeficiente 2:



Tarea: ¿por qué en el segundo caso, Lenin primero se convierte en Dzerzhinsky, y luego converge nuevamente a Lenin, pero de mayor tamaño?

Conclusión

Se pueden formular muchas tareas de procesamiento de datos, en particular, geometría, como una solución a un sistema de ecuaciones lineales. En este artículo no dije cómo construir estos sistemas, mi objetivo era solo demostrar que esto es posible. El tema del próximo artículo ya no será "por qué", sino "cómo" y qué solucionadores usará más adelante.

Por cierto, y después de todo en el título del artículo hay mínimos cuadrados. ¿Los viste en el texto? Si no, entonces esto no da miedo, esta es exactamente la respuesta a la pregunta "¿cómo?". Manténgase en línea, en el próximo artículo le mostraré exactamente dónde se esconden y cómo modificarlos para obtener acceso a una herramienta de procesamiento de datos extremadamente poderosa. Por ejemplo, en diez líneas de código puede obtener esto:



¡Estén atentos para más!