Mejorando la calidad de pegar panoramas al hacer coincidir el gráfico de transformaciones proyectivas

Hola Habr! Hoy hablaremos sobre una de las formas de mejorar la calidad de los panoramas de pegado. Existe un enfoque ampliamente utilizado para pegar panoramas de objetos planos, pero dado que este enfoque no está exento de inconvenientes, ofrecemos nuestra mejora.

La tarea de paneo es construir una imagen compuesta basada en un conjunto de imágenes de origen (ver Fig. 1). Encuentra aplicación en la resolución de problemas prácticos como:

• sondeo de la superficie de la Tierra desde un satélite o desde un avión no tripulado;
• pegar imágenes obtenidas usando un microscopio;
• pegar video;
• Super resolución de captura de imagen.

Figura 1 - Imágenes originales y panorama

En general, el algoritmo de pegado panorámico se puede formular de la siguiente manera [1] (ver Fig. 2). Al principio, se requiere extraer una cantidad suficiente de cuadros del flujo de video. Esto se puede hacer en línea, leyendo secuencialmente todos los cuadros y seleccionando cuadros individuales con la frecuencia necesaria.

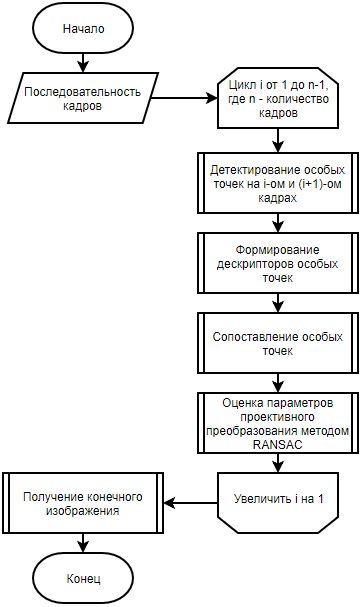
Figura 2: diagrama de flujo del algoritmo de pegado panorámico con puntos especiales

Después de eso, ordenando secuencialmente a través de pares de imágenes del conjunto, es necesario detectar puntos singulares y calcular sus descriptores en estas imágenes [2–4]. Son estos puntos singulares los que nos permiten construir una correspondencia geométrica entre dos cuadros. La siguiente es una comparación de puntos singulares en función de sus descriptores. Debe tenerse en cuenta que esto no excluye la posibilidad de obtener coincidencias falsas.

Además, al tener dos conjuntos de puntos singulares, uno debe encontrar una transformación proyectiva que traduzca los puntos de un cuadro a los puntos correspondientes de otro de la mejor manera. Para resolver este problema, se puede utilizar el enfoque RANSAC [5]. Este enfoque se describe con más detalle en [6, 7]

Para buscar una transformación proyectiva entre cuadros, también se puede usar una corriente óptica, que a menudo se usa en la tarea de pegar panoramas [8].
Después de obtener el conjunto requerido de transformaciones proyectivas, se lleva a cabo un procedimiento técnico para pegar imágenes, a saber: para cada píxel del panorama final (x, y) para cada canal (RGB), el promedio aritmético de las intensidades de píxeles con las coordenadas (x, y) de todos los cuadros, incluidos un píxel con tales coordenadas.

Usando los métodos de búsqueda de transformaciones proyectivas, se puede determinar el desplazamiento de la posición de la cámara en relación con la posición anterior en el espacio. En condiciones de laboratorio, la precisión del cálculo de estos datos es suficiente para construir un panorama de un objeto estacionario plano. En condiciones reales, al calcular el desplazamiento de la posición de la cámara con respecto a la posición anterior, se produce un error de cálculo (error de medición / interferencia / limitaciones impuestas por algoritmos, etc.). Con el tiempo, el error acumulativo continúa aumentando de tal manera que, a pesar de la precisión aceptable de determinar el desplazamiento entre posiciones adyacentes, el panorama general del objeto ya contendrá desviaciones graves (ver Fig. 3).

Figura 3 - Error acumulativo

Nos propusimos el objetivo de desarrollar un método para hacer coincidir el gráfico de transformaciones proyectivas para la tarea de encuadrar objetos fijos planos que sea resistente al problema de acumular errores. Otro objetivo es desarrollar el método de tal manera que no dependa del método de cálculo de los parámetros de la transformación proyectiva.

Se debe cumplir una de las condiciones:

• disparar un objeto estacionario pseudo-rígido;
• disparo de un objeto cercano al plano desde una distancia suficientemente grande;
• para todas las posiciones de la cámara durante el disparo, se cumple el requisito: para todos los puntos de imagen, los rayos que conectan estos puntos con el enfoque de la cámara no coinciden entre sí.

Descripción del algoritmo de coincidencia del gráfico de transformación de proyección

Introducimos el concepto de un sistema de coordenadas único. Por un solo sistema de coordenadas nos referimos a un sistema de coordenadas donde los mismos puntos de un objeto de diferentes imágenes tendrán las mismas coordenadas. Este requisito puede expresarse mediante la siguiente fórmula:

$$

$$f (x) = y,$$

donde $$$f$Es un mapeo definido en la parte común de los cuadros y traduce los puntos del primer cuadro a los puntos del segundo cuadro, $$$x$- coordenadas del punto en el sistema de coordenadas del primer cuadro, $$$y$- coordenadas de un punto en el sistema de coordenadas del segundo cuadro.

En el caso cuando el mapeo $$$f$puede continuar correctamente más allá de la intersección de cuadros, podemos complementar el segundo cuadro con información del primero. Por lo tanto, se obtendrá un mapa pegado como un mosaico de dos o más cuadros.

Después de encontrar las transformaciones proyectivas entre los cuadros adyacentes, hay un pegado inicial que establece la ubicación única de los cuadros en un solo sistema de coordenadas (ver Fig. 4).

Figura 4: la ubicación inequívoca del marco en el mapa

Después de construir el pegado primario de imágenes, se construye un gráfico de transformaciones proyectivas $$$G$:

$$

$$G = (V, E),$$

donde $$$V$- una gran cantidad de cuatro puntos, que son los vértices de las imágenes corregidas proyectivamente; $$$\ vert V \ vert = n$, $$$E$- muchas transformaciones proyectivas entre cuadros; $$$\ vert E \ vert = m$.

Un borde entre los vértices se construye solo si los marcos se cruzan al menos en $$$T \%$en el encolado primario (IoU - Intersección sobre Unión) (ver. Fig. 5, 6):

$$

$$\ frac {s_ {ij}} {s_i + s_j-s_ {ij}} \ cdot100 \%> T \%.$$

Figura 5 - Área de intersección del marco

Umbral $$$T$se selecciona según el método utilizado para buscar una transformación proyectiva al equilibrar entre la condicionalidad de la tarea de buscar una transformación proyectiva entre dos cuadros y el número esperado de aristas y ciclos en el gráfico.

Figura 6 - Un ejemplo de construcción gráfica

Como resultado, la gráfica de transformaciones proyectivas $$$G$se ve de la siguiente manera (ver Fig. 7):

Figura 7 - El gráfico final de transformaciones proyectivas

Si el gráfico contiene ciclos (ver Fig. 6), aparece información redundante en él, que también puede contener contradicciones. Para determinar qué tipo de contradicciones pueden surgir, consideramos un cierto ciclo del gráfico (ver Fig. 8). Deje que este ciclo consista en vértices $$$1,2, ..., k$. Luego tenemos una serie de mapeos proyectivos a lo largo de este ciclo:

$$

$$H_ {12}: 1 \ to2, \\ H_ {23}: 2 \ to3, \\ ... \\ H_ {k1}: k \ to1. \\ $$

Considere la composición de estas asignaciones:

$$

$$H_ {k1} * ... * H_ {23} * H_ {12} = H_ {11}.$$

Figura 8 - Bucle de gráfico

Display $$$H_ {11}$debe ser un mapeo idéntico. Si el mapeo $$$H_ {11}$diferente de lo idéntico, entonces decimos que se obtiene una contradicción. En este caso, el ciclo se llamará inconsistente . Por lo tanto, existe un problema asociado con la presencia de ciclos inconsistentes en el gráfico de mapeos proyectivos, ya que con un pegado perfecto las contradicciones en el gráfico de transformaciones proyectivas $$$G$debe estar ausente

Describimos el algoritmo de coincidencia para el gráfico de transformaciones proyectivas, es decir, la coincidencia de todos sus ciclos. Para minimizar el error acumulativo que ocurre cuando el ciclo se cierra en el gráfico de transformaciones proyectivas, se utiliza el concepto del método SLAM (localización y mapeo simultáneo) [9].

Considere en cada cuadro cuatro puntos en posición general. Deje que los marcos estén numerados $$$1$antes $$$n$entonces cuatro puntos serán denotados por $$$p_i$donde $$$1 \ le i \ le n$. Tal conjunto de cuatro puntos $$$P$define de forma única un sistema de coordenadas único, ya que para cualquiera de los dos cuadros puede encontrar de manera única un mapa proyectivo que traduzca uno cuatro puntos a otro.

Para encontrar el conjunto de cuatro puntos que determinarán el gráfico consistente deseado, puede usar el método de mínimos cuadrados. Minimizamos lo funcional, que es igual a la suma sobre todos los bordes del conjunto $$$E$contar $$$G$y para cada borde: la suma de cuatro puntos de cantidades $$$\ Vert H_ {ij} p_ {is} -p_ {js} \ Vert$. Para encontrar una solución que minimice lo funcional, se propone utilizar el método de gradiente conjugado.

$$

$$\ sum _ {(i, j) \ en E} \ sum_ {s = 1} ^ 4 \ Vert H_ {ij} p_ {is} -p_ {js} \ Vert \ to \ min_ {P}.$$

Después de que haya una transformación proyectiva para cada cuadro que establezca de manera única la posición del cuadro en el mapa, puede obtener una imagen panorámica.

Resultados experimentales

Hasta la fecha, no existe un método universal para evaluar la calidad de las imágenes pegadas. Como regla general, la calidad del encolado es evaluada organolépticamente por expertos, pero para la investigación científica es preferible tener una evaluación de calidad cuantitativa y calculada automáticamente.

Para evaluar la calidad del encolado sin la participación de un experto humano, es necesario tener un encolado estándar con el que se comparará el resultado. El enfoque en el que se obtuvo el encolado a partir de un video real, y la fotografía de todo el objeto se considera como el encolado estándar, requiere buenas condiciones de laboratorio utilizando un manipulador que sea capaz de fijar físicamente (usando sensores) la posición de la cámara en el espacio. Sin embargo, este método de evaluación de calidad es costoso.

En [10], para una evaluación cuantitativa de la calidad de la vinculación panorámica, los autores, que tienen una imagen de alta resolución, crean un video artificial cuyos marcos son áreas distorsionadas proyectivamente de la imagen original (ver Fig. 9). Proyectivamente distorsionó todos los cuadros excepto el primero, ya que se especifica un único sistema de coordenadas en relación con el primer cuadro. Además, estos cuadros de video artificial se pegan en un panorama, que se compara aún más con la imagen de referencia original. Con este enfoque, es posible evitar los problemas de la diferencia en el brillo de los encolados obtenidos y de referencia, así como la distorsión de la escena.

Figura 9 - Imagen original y cuadros de video artificial

Para comparar la calidad del pegado antes y después de acordar un gráfico, se preparó una muestra de prueba de 50 imágenes, se crearon 50 videos artificiales a partir de las imágenes originales, según las cuales se realizó el pegado (ver Fig. 10). Todos los panoramas obtenidos se redujeron al tamaño de las imágenes de origen, y para cada panorama se calculó la medida de error:

$$

$$RMSE = \ sqrt {\ frac {\ sum_ {i = 1} ^ h \ sum_ {j = 1} ^ w ((I_ {ij} ^ R- \ hat {I_ {ij} ^ R}) ^ 2+ (I_ {ij} ^ G- \ hat {I_ {ij} ^ G}) ^ 2+ (I_ {ij} ^ B- \ hat {I_ {ij} ^ B}) ^ 2)} {h \ cdot w \ cdot 3}},$$

donde $$$h$- altura de la imagen $$$w$- ancho de imagen $$$I_ {ij} ^ R$- intensidad de píxeles $$$(i, j)$el panorama resultante en el canal rojo ( $$$G$- canal verde $$$B$- canal azul) $$$\ hat {I_ {ij} ^ R}$- intensidad de píxeles $$$(i, j)$imagen de origen en el canal rojo ( $$$G$- canal verde $$$B$- canal azul).

Figura 10 - Panorama antes del acuerdo del gráfico (RMSE = 35.3) y después (RMSE = 14.2)

En la representación gráfica, el RMSE en el conjunto de prueba tiene el siguiente aspecto (ver Fig. 11):

Figura 11 - RMSE en la muestra de prueba. Los marcos se ordenan en orden ascendente de RMSE hasta la coincidencia de gráficos.

De acuerdo con cada valor raíz del error cuadrático medio antes de hacer coincidir, se presentan los valores raíz del error cuadrático medio después de hacer coincidir el gráfico. El valor medio de RMSE en la muestra de prueba antes de que el gráfico sea consistente es 35.5 , después de que el gráfico coincida - 13.9 .

Conclusión

Con base en los resultados de comparar la calidad del encolado, podemos concluir que la coincidencia del gráfico reduce significativamente el error acumulado y mejora la calidad de los panoramas de encolado. Sin embargo, debe tenerse en cuenta que la correspondencia de gráficos solo puede ayudar si hay ciclos en el gráfico de transformaciones proyectivas. En ausencia de ciclos en el gráfico de transformaciones proyectivas, el módulo de correspondencia de gráficos no afecta la calidad del pegado panorámico.

Vale la pena señalar que este método de comparación de gráficos funciona con un conjunto de transformaciones proyectivas, y la forma en que se encontraron estas transformaciones proyectivas no juega un papel para este método.

En el futuro, se planea optimizar la complejidad del algoritmo, ya que es aplicable solo a casos de usuarios "fuera de línea".

Literatura

[1] Gubin A.Yu., Kovin R.V. Un enfoque simple para la tarea de pegar imágenes superpuestas en un panorama // X Conferencia Internacional Científica y Práctica de Estudiantes, Estudiantes de Posgrado y Jóvenes Científicos "Juventud y Tecnologías de la Información Modernas", pág. 79-81, 2012.
[2] Drummond T., Rosten E. Aprendizaje automático para la detección de esquinas a alta velocidad // Novena Conferencia Europea sobre Visión por Computadora (ECCV), p. 430-443, 2006.
[3] Características distintivas de la imagen de Lowe DG desde puntos clave invariables a escala // International Journal of Computer Vision, p. 91-110, 2004.
[4] Bay H., Ess A., Yuitelaars T., Van Gool L. SURF: Aceleraron características robustas // Visión por computadora y comprensión de imágenes, v. 110, p. 346-359, 2008.
[5] Martin A. Fischler, Robert C. Bolles. Consenso de muestras aleatorias: un paradigma para el ajuste de modelos con aplicaciones para análisis de imágenes y cartografía automatizada // Comm. de la ACM, v. 24, p. 381-395, 1981.
[6] Arlazarov V.L., Bulatov K.B., Chernov T.S. El método de búsqueda de imágenes difusas en grandes volúmenes de datos de video // Sistemas de alta disponibilidad, Vol. 12, No. 1, p. 53-58, 2016.
[7] Skoryukina N. y col. Snapscreen: búsqueda de cuadros de transmisión de TV con consulta proyectiva distorsionada y ruidosa // Novena Conferencia Internacional sobre Visión Artificial (ICMV) - Proc. SPIE V.10341, p. 103410Y, 2017.
[8] Bouguet JY Implementación piramidal del rastreador de características afines lucas kanade: descripción del algoritmo // Intel corporation, V. 5, p. 1-10, 2001.
[9] Newman P., Ho K. Cierre SLAM-loop con características visualmente destacadas // IEEE Proc. de la Conferencia Internacional sobre Robótica y Automatización, p. 635-642, 2005.
[10] Paalanen P., Kamarainen JK, Kalviainen H. Evaluación cuantitativa de mosaicos basada en imágenes con video artificial // Conferencia escandinava sobre análisis de imágenes, Springer (Berlín, Heidelberg), p. 470-479, 2009.