Los científicos confunden confusamente que todavía no conocen la magnitud exacta de la interacción gravitacional

Según la leyenda, el primer experimento, que mostró que todos los objetos caen a la misma velocidad, independientemente de la masa, fue realizado por Galileo Galilei, de pie en la cima de la Torre Inclinada de Pisa. Cualquiera de los dos objetos arrojados en el campo gravitacional, en ausencia de resistencia del aire (o descuidándolo) se acelerará por igual. Más tarde, esta regla fue brevemente escrita por Newton después de estudiar este tema.

Por primera vez comenzamos a formular las leyes de la física, lo hicimos empíricamente: a través de experimentos. Lanza la pelota desde la torre, como podría haber hecho Galileo, y puedes medir cuánto volará y después de qué hora caerá. Suelte el péndulo, y puede encontrar la relación entre su longitud y la cantidad de tiempo durante un período. Después de hacer esto con varias distancias, longitudes e intervalos de tiempo, comenzará a notar el sistema: la altura del objeto es proporcional al cuadrado del tiempo, el período del péndulo es proporcional a la raíz cuadrada de su longitud.

Pero para convertir las proporciones en ecuaciones, debe elegir una constante.


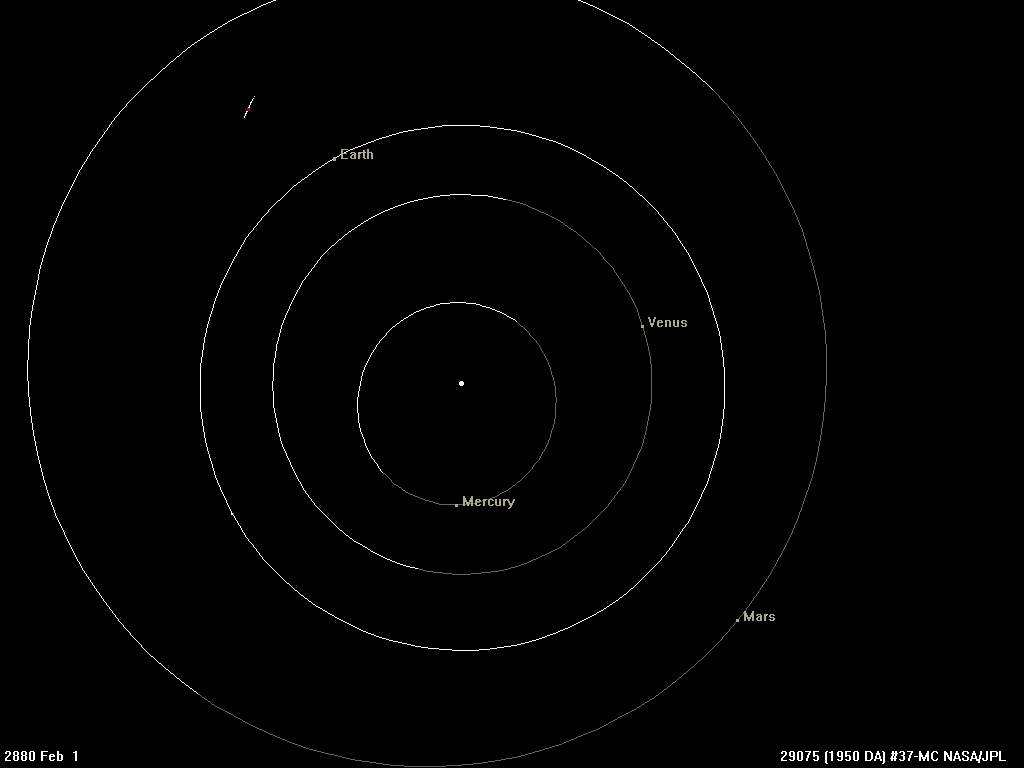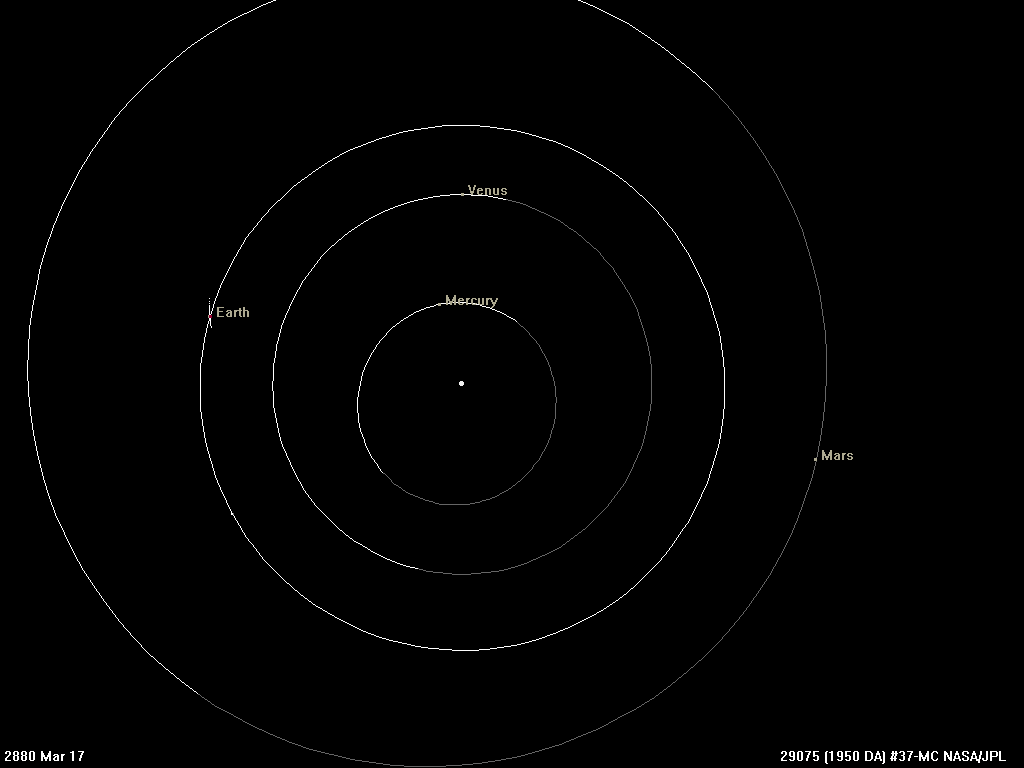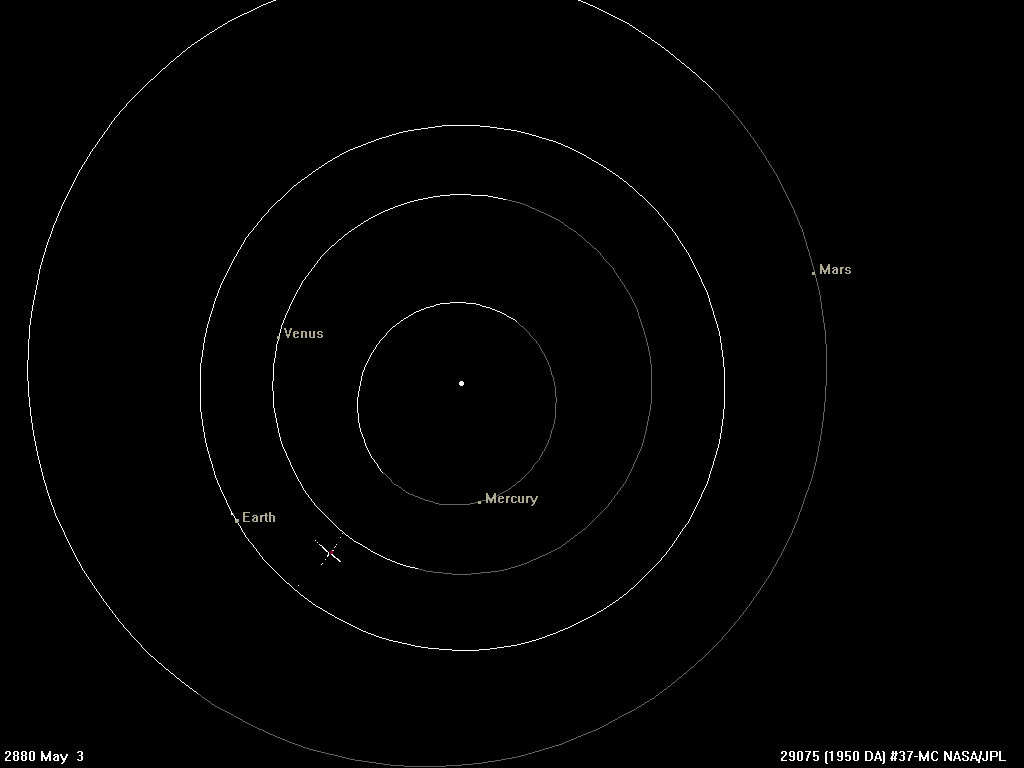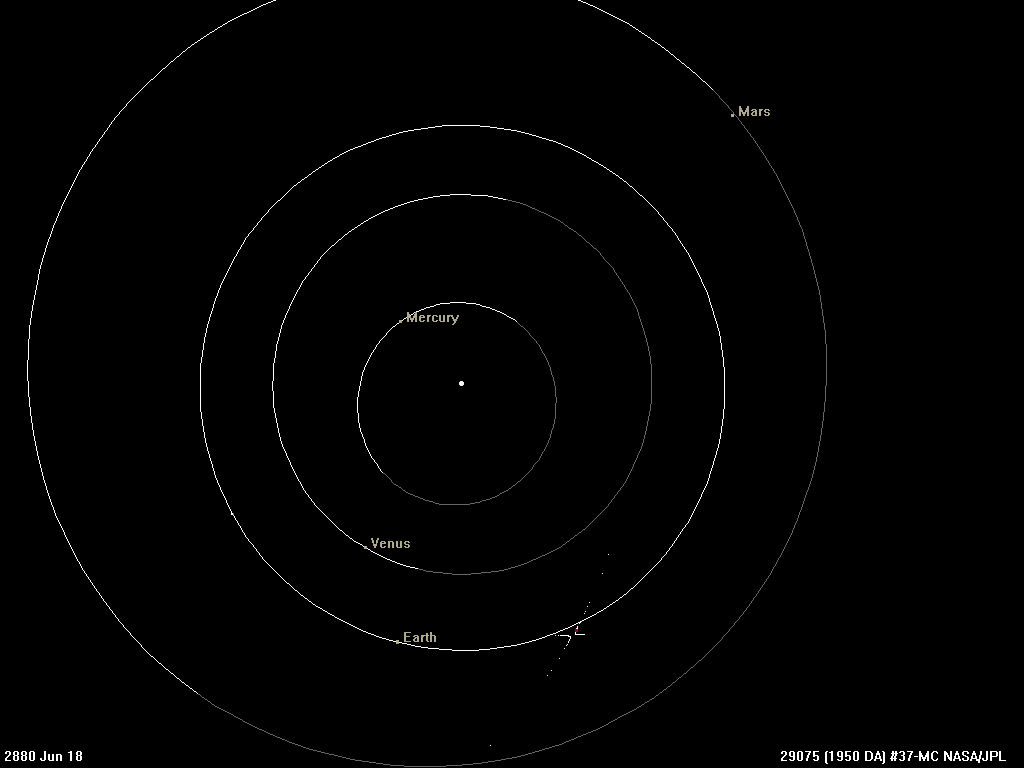Las órbitas de los planetas del sistema solar interno no son perfectamente redondas, sino cercanas a círculos. Mercurio y Marte se desvían más del ideal, lo que demuestra la elipticidad de las órbitas. A mediados del siglo XIX, los científicos comenzaron a notar las desviaciones de Mercurio de las predicciones de la gravedad newtoniana, que solo la Relatividad General en el siglo XX podía explicar. La misma ley de gravedad, y la misma constante, describen el efecto de la gravedad en todas las escalas, desde la Tierra hasta el espacio.

En estos ejemplos, y en muchos otros, el papel de la constante de proporcionalidad es G, la constante gravitacional . La luna se mueve alrededor de la Tierra, el planeta - alrededor del Sol, la luz se distorsiona por lentes gravitacionales, los cometas pierden energía, escapan del sistema Solar - y todo esto sucede en proporción a G. Incluso antes de Newton, en las décadas de 1640 y 1650, los científicos italianos Francesco Grimaldi y Giovanni Riccioli realizó los primeros cálculos de la constante gravitacional, lo que significa que se convirtió en la primera de todas las constantes fundamentales determinadas, incluso antes de la determinación de la velocidad de la luz en 1676, realizada por Ole Römer .


La ley de gravedad de Newton ha sido reemplazada por la Teoría general de la relatividad de Einstein. Se basó en una acción instantánea de largo alcance y fue extremadamente sencillo. El valor de la constante gravitacional G de esta ecuación todavía es muy poco conocido.

Si tomas dos masas en el Universo y las colocas cerca una de la otra, se sentirán atraídas. De acuerdo con las leyes de Newton, aplicables a todas las masas, excepto a las extremadamente grandes, y para todas las distancias pequeñas, la fuerza gravitacional está asociada con ambas masas, separándolas por la distancia y la constante gravitacional G. Durante varios siglos hemos refinado nuestras mediciones de muchas constantes fundamentales con una precisión increíble. La velocidad de la luz c se conoce exactamente: 299,792,458 m / s. La constante de Planck ħ que controla las interacciones cuánticas tiene un valor de 1.05457180 × 10 ^-34 J * s, con un error de ± 0.000000013 × 10 ^-34 J * s.

Pero con G viene un asunto completamente diferente.


Ya sea que usemos la descripción de la gravedad de Newton o Einstein, la magnitud de la fuerza está determinada, en particular, por la magnitud de la constante gravitacional G, cuyo valor debe medirse experimentalmente y no puede deducirse de otros.

En la década de 1930, para el valor G, se obtuvieron 6.67 × ^10-11 N * m ² / kg ² , en la década de 1940 se refinó a 6.673 × 10-11 N * m ² / kg ² , y ambas mediciones fueron realizadas por Paul Hale . Como era de esperar, con el tiempo, los valores mejoraron constantemente, y el error cayó del 0.1% al 0.04%, y alcanzó el 0.012% a fines de la década de 1990 gracias al trabajo de Barry Taylor de NIST.

Si observa la copia anterior del folleto de datos de partículas, en la que se dieron los valores de las constantes fundamentales, puede encontrar el valor G de 6.67259 × 10-11 N * m ² / kg ² , con un error de solo 0,00085 × 10 ^{- 11} N * m ² / kg ² .


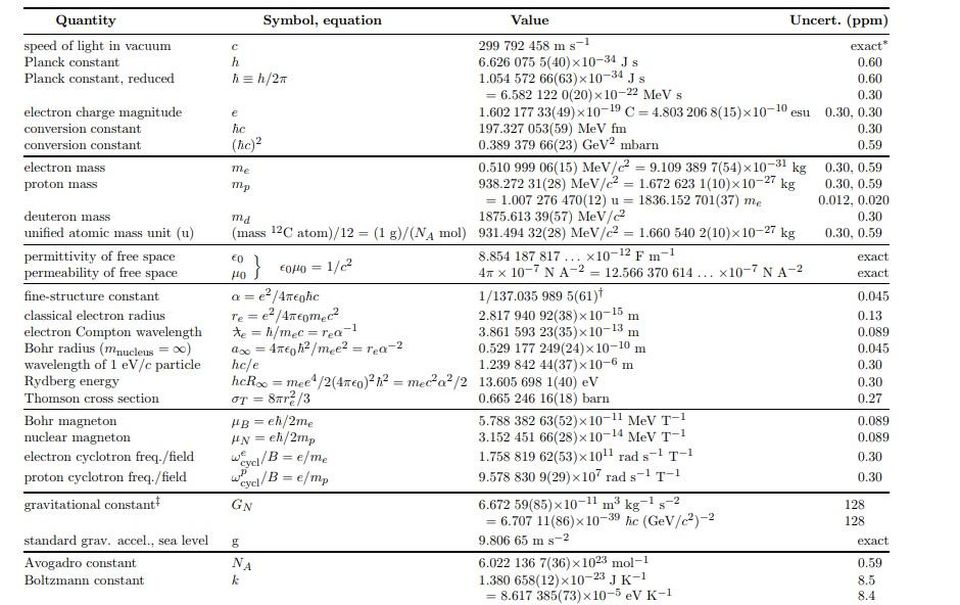Los valores de las constantes fundamentales para 1998

Y entonces sucedió algo gracioso.

Más tarde ese año, los experimentos revelaron un valor que era demasiado alto para el valor indicado: 6.674 × 10-11 N * m ² / kg ² . Los diferentes equipos que utilizan diferentes métodos recibieron valores de G que no coincidieron entre sí en un 0,15%, que es más de diez veces el error informado anteriormente.

¿Cómo sucedió esto?


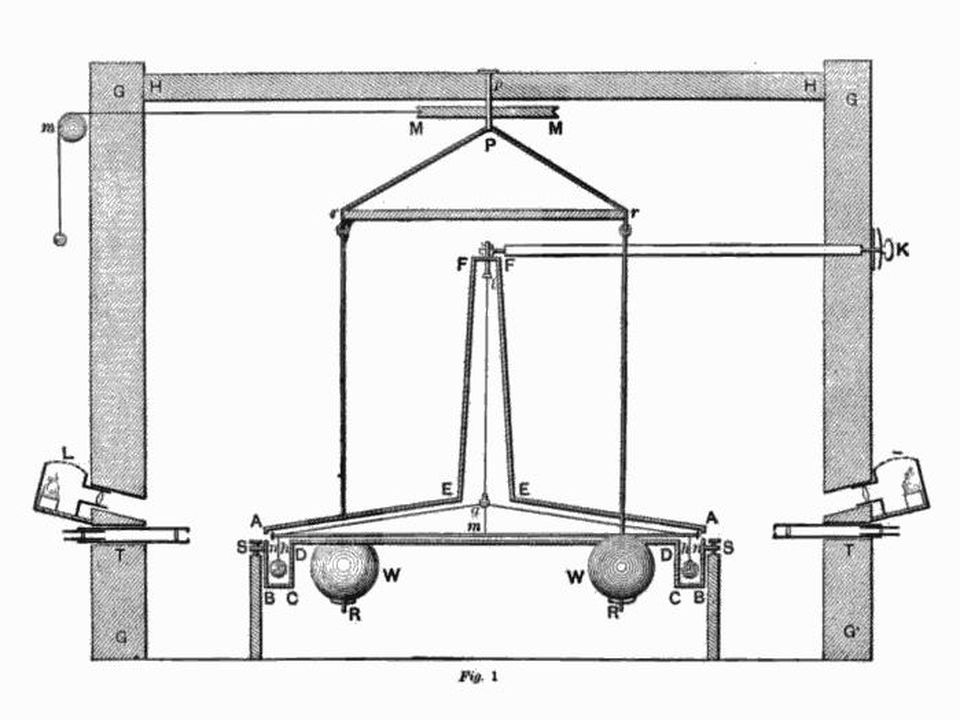El experimento inicial sobre la medición exacta de G, desarrollado y publicado por Henry Cavendish , se basa en el principio de los pesos de torsión , girando dependiendo de la atracción gravitacional de una masa cercana de una cantidad conocida.

La primera medición precisa de la constante gravitacional, independiente de otras incógnitas (por ejemplo, la masa del Sol o la masa de la Tierra) tuvo lugar solo en el experimento de Henry Cavendish a fines del siglo XVIII. Cavendish desarrolló un experimento conocido como equilibrio de torsión en el que se suspendió una pequeña pesa y se equilibró perfectamente en un cable. Cerca de cada una de las masas al final de la mancuerna había dos masas más grandes, que atraían gravitacionalmente a las masas pequeñas. El valor de la rotación de la pesa a distancias y masas conocidas nos dio la oportunidad de medir G experimentalmente.


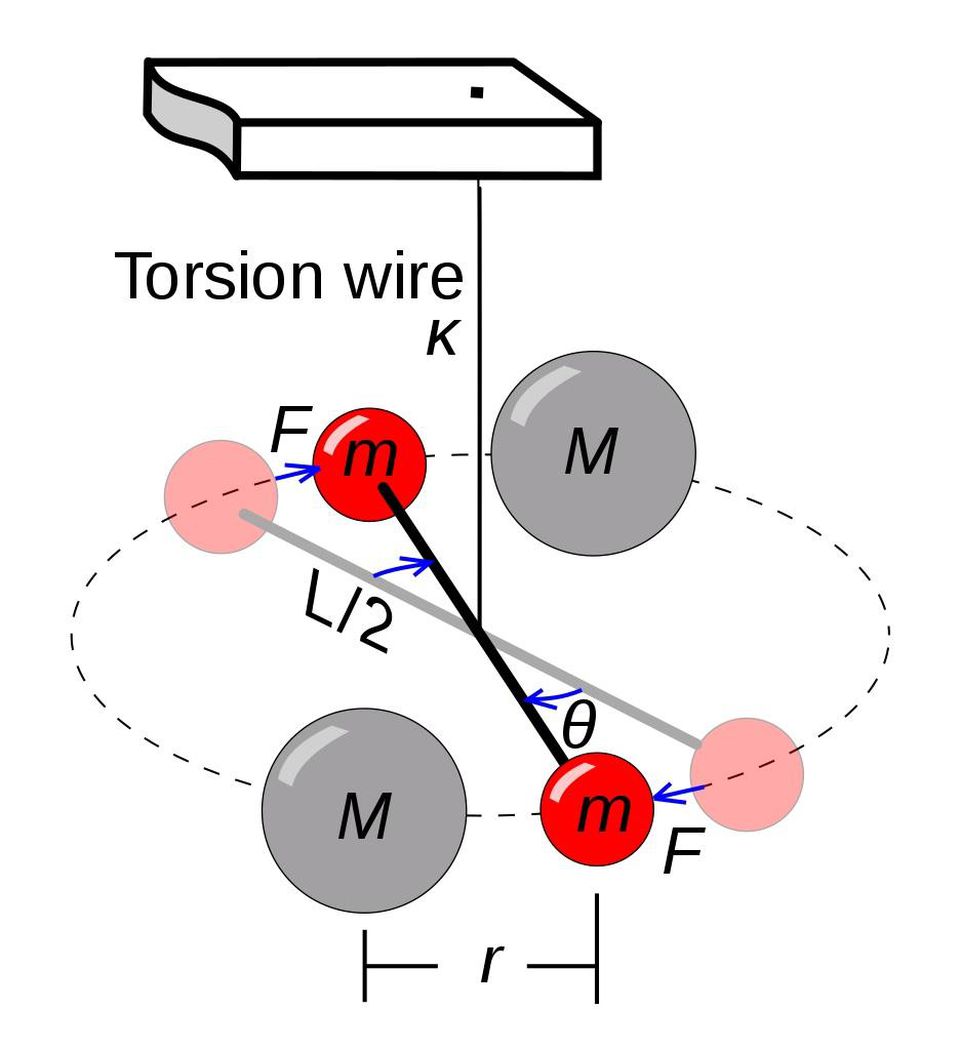A pesar de muchos avances en física en los últimos 200 años, el mismo principio utilizado en el experimento Cavendish se utiliza en los experimentos de medición G. Hasta hoy, ninguna otra técnica de medición o dispositivo experimental ha dado mejores resultados.

Existe la sospecha de que una de las razones de las discrepancias es el conocido factor psicológico del sesgo de confirmación . Si todos sus colegas obtienen un resultado de la forma 6.67259 × 10-11 N * m ² / kg ² , es razonable esperar que también recibirá un resultado del tipo 6.67224 × 10-11 N * m ² / kg ² , o 6.67293 × ^10-11 N * m ² / kg ² ; pero si obtiene algo como 6.67532 × 10-11 N * m ² / kg ² , decidirá que hizo algo mal.

Buscará fuentes de error hasta que lo encuentre. Repetirá el experimento una y otra vez hasta que obtenga algo razonable: algo que no contradiga el valor de 6.67259 × 10-11 N * m ² / kg ² .


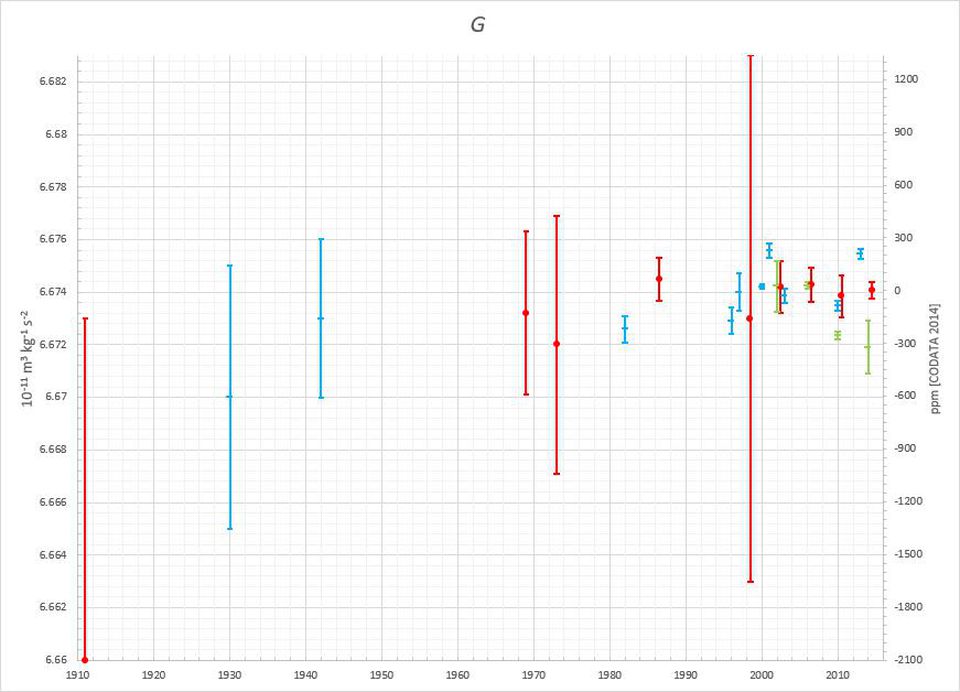En 1997, el equipo de Bagley y Luther realizó un experimento con un equilibrio de torsión que arrojó un resultado de 6.674 × 10-11 N * m ² / kg ² , que se tomó lo suficientemente en serio como para poner en duda el error de medición anterior G

Por lo tanto, tal conmoción fue el evento de 1998, cuando un equipo que trabajó con mucho cuidado recibió un resultado que difería en un increíble 0.15% de los anteriores, mientras que los errores declarados de las mediciones anteriores fueron diez veces menores. En respuesta, el NIST rechazó los errores anteriores, y los valores resultantes se redujeron a cuatro dígitos significativos, y el error se incrementó.

Las escalas de torsión y los péndulos de torsión, realizados bajo la influencia del experimento Cavendish original, continúan liderando las mediciones de G, por delante de las tecnologías de interferometría atómica más modernas. Solo en agosto, el equipo chino anunció la recepción del valor G más preciso de dos mediciones independientes: 6.674184 × 10-11 N * m ² / kg ² y 6.674484 × 10-11 N * m ² / kg ² con errores en 0.0011%.


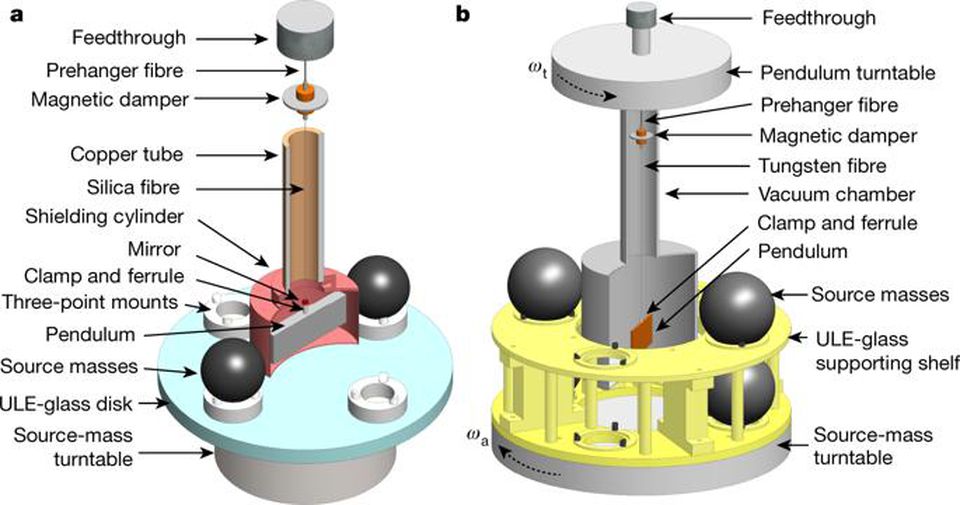Dos instalaciones experimentales, cuyos esquemas se publicaron en Nature 2018 en agosto de 2018, dieron los valores más precisos (según los científicos) para G

Estos valores son consistentes entre sí dentro de dos desviaciones estándar, pero no son consistentes con otras mediciones tomadas por otros equipos en los últimos 15 años, que varían de 6.6757 × 10-11 N * m ² / kg ² a 6.6719 × 10 ^{- 11} N * m ² / kg ² . Si bien se conocen otras constantes fundamentales con una precisión de 8 a 14 dígitos significativos, al medir G, los errores son miles o miles de millones de veces más grandes.


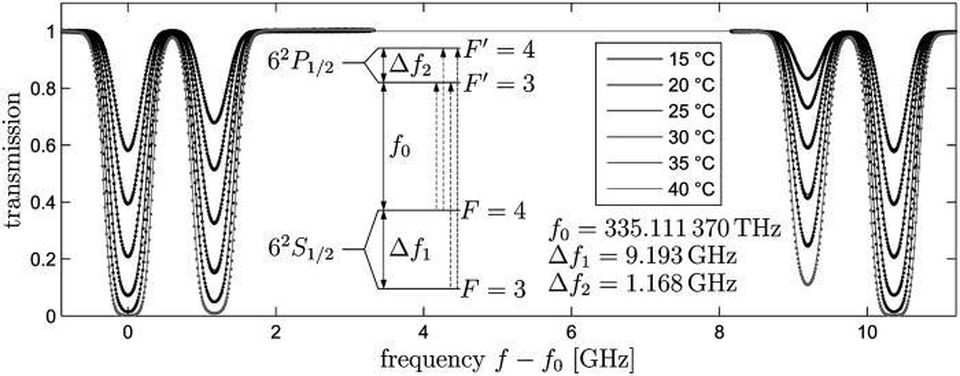La transición atómica del orbital 6S, Delta_f1, determina el medidor, el segundo y la velocidad de la luz. La precisión de determinar las constantes cuánticas es miles de veces mayor que la precisión de medir G, la primera de las constantes medidas.

La constante gravitacional del Universo, G, fue la primera de las medidas. Sin embargo, 350 años después de la primera medición, es vergonzoso decir cuán poco se conoce en comparación con todos los demás. Utilizamos esta constante en una gran cantidad de mediciones y cálculos, desde ondas gravitacionales hasta púlsares, midiendo la expansión del Universo. Sin embargo, nuestra capacidad para determinarlo se basa en experimentos a pequeña escala realizados en la Tierra. Pequeñas fuentes de incertidumbre, desde la densidad de los materiales hasta las vibraciones sísmicas, penetran nuestros intentos de medirlo. Y hasta que podamos lograr más, donde sea que la gravedad sea importante, habrá un error interno desagradablemente grande. Es 2018, y todavía no sabemos cuán grande es realmente la gravedad.

Puede encontrar más artículos sobre el tema de la ciencia popular en el sitio web Golovanov.net . Leer: es la tectónica de placas necesaria para la formación de la vida en el planeta; ¿De dónde viene la energía en la energía oscura? si la actividad humana conducirá a una guerra interestelar; ¿Hay una cantidad saludable de alcohol? La serie de artículos de cosmología Ask Ethan .

No dude en apoyar el proyecto financieramente (tarjetas bancarias, Yandex.Money, WebMoney, Bitcoins, pero lo que sea). ¡Gracias a todos los que ya han brindado apoyo!