Procesos de oleaje en líneas hidráulicas. Los fundamentos

Hola Habr!

En un artículo anterior hablé sobre el método de características, diseñado para calcular procesos de ondas en líneas hidráulicas. De hecho, por supuesto, los procesos de onda se pueden calcular en la mente, solo necesita conocer el enfoque.

Debajo del corte, mostraré "en los dedos" y con la ayuda de gifs los principales efectos de onda. Como ejemplo, volveré a usar la línea hidráulica, pero de hecho, se basan en casi las mismas ecuaciones que para las líneas acústicas y eléctricas. Entonces, incluso si no es hidráulico, puede haber analogías simples para ayudarlo a comprender los procesos de onda en general.

Precaución ¡Debajo del gato, 15 MB de gifs animados!

Entonces, aquí consideraremos la propagación de ondas planas unidimensionales en una línea hidráulica. Esta suposición es bastante cierta para tuberías largas, cuya longitud es muchas veces mayor que el diámetro interno. Por simplicidad, también descuidamos la fricción por ahora. En este caso, los procesos físicos en curso se describirán mediante un par de ecuaciones diferenciales parciales:

$$

$$\ frac {\ partial p} {\ partial t} + \ rho \; c ^ 2 \ frac {\ partial v} {\ partial x} = 0$$

$$

$$\ frac {\ partial v} {\ partial t} + \ frac1 \ rho \ frac {\ displaystyle \ partial p} {\ displaystyle \ partial x} = 0$$

donde $$$\ rho$ - densidad $$$v$ - velocidad $$$p$ - presión $$$c$ - velocidad del sonido.

Por costumbre, el aspecto de estas ecuaciones puede asustar, pero de hecho, todo es simple aquí. La primera ecuación nos dice que la presión aumentará con el tiempo si fluye más líquido hacia el segmento de la tubería de lo que sale (además, cuanto más rápido, más denso y elástico es el líquido en la tubería); la segunda ecuación muestra que para acelerar un segmento de un líquido, es necesario aplicarle una diferencia de presión (además, cuanto mayor es la densidad, más diferencia de presión debe aplicarse para acelerar el segmento). Es decir Se describen cosas bastante banales: el fluido es compresible, el fluido tiene una masa.
Dejemos la solución analítica de estas ecuaciones para futuros artículos, pasemos inmediatamente al ejemplo "en los dedos".
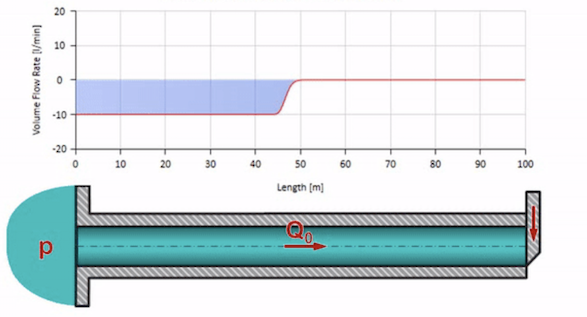
Tome una tubería llena de agua en la que se mantenga una presión de 100 bar (10 MPa) y un caudal de 30 l / min. Si se aplica un paso de presión al extremo izquierdo, previsiblemente comenzará a moverse a lo largo de la corriente a una velocidad igual a la velocidad del sonido en el medio.

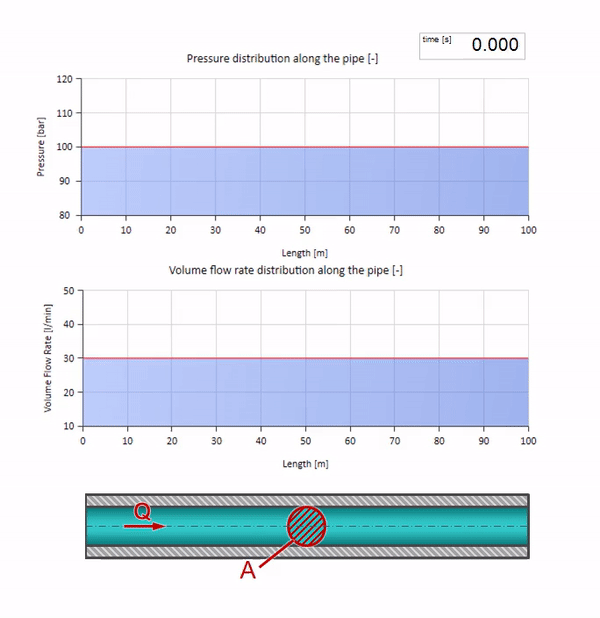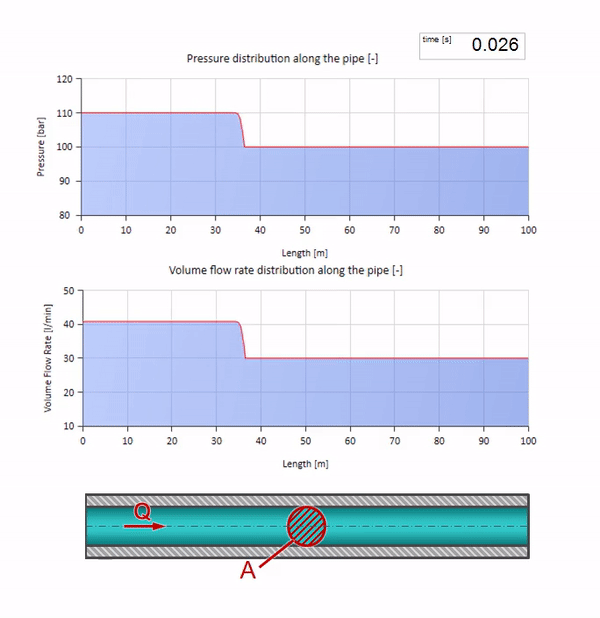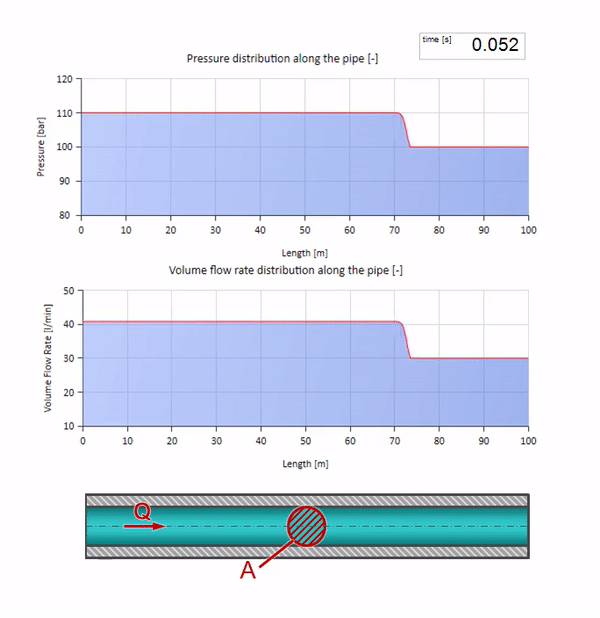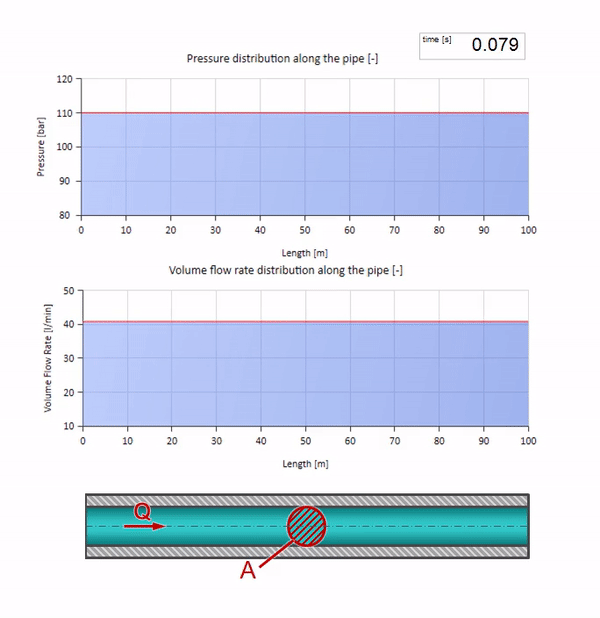
Por supuesto, con la presión, el caudal también cambiará. Si la presión aumenta, “ajustará” el fluido aguas arriba y aumentará el caudal en algún “paso” también. Cuánto está determinado por el valor de la impedancia de onda. Para una tubería con un área de sección transversal $$$A$ lleno de líquido con densidad $$$\ rho$ y velocidad local del sonido $$$c$ , la impedancia de onda se puede calcular de la siguiente manera:

$$

$$Z_L = \ frac {\ rho \; c} A$$

En términos de dimensiones, esto es lo mismo que la resistencia hidráulica convencional, solo utilizada para calcular las relaciones de onda de presión ( $$$\ widehat p$ ) y caudal ( $$$\ widehat Q$ ), y no sus valores absolutos:

$$

$$Z_L = \ frac {\ widehat p} {\ widehat Q}$$

Cuanto mayor es la densidad y la velocidad del sonido, mayor es la impedancia de onda, es decir cuanto más difícil sea para una cierta caída de presión dispersar el líquido (aumentar el flujo)

Ahora veamos cómo se moverán dos olas, moviéndose una hacia la otra:

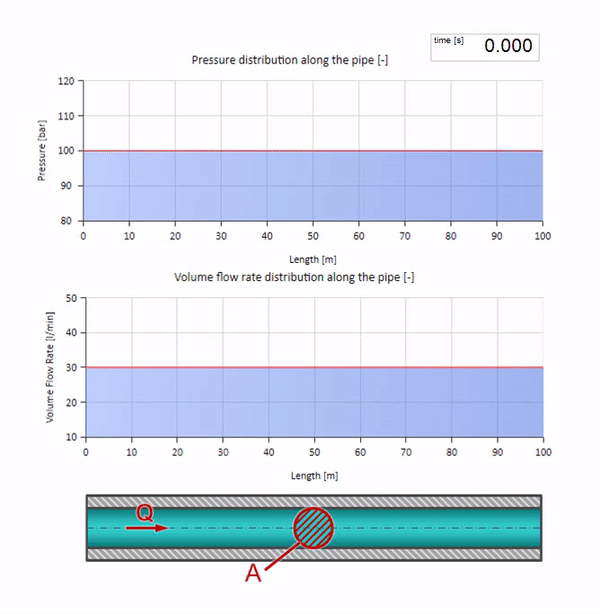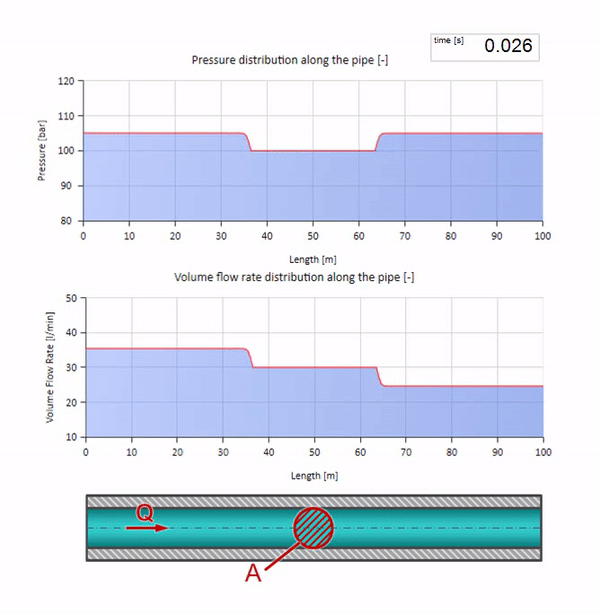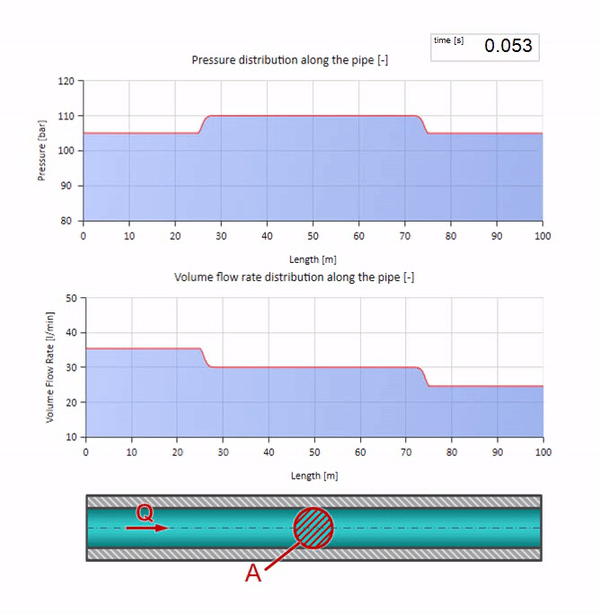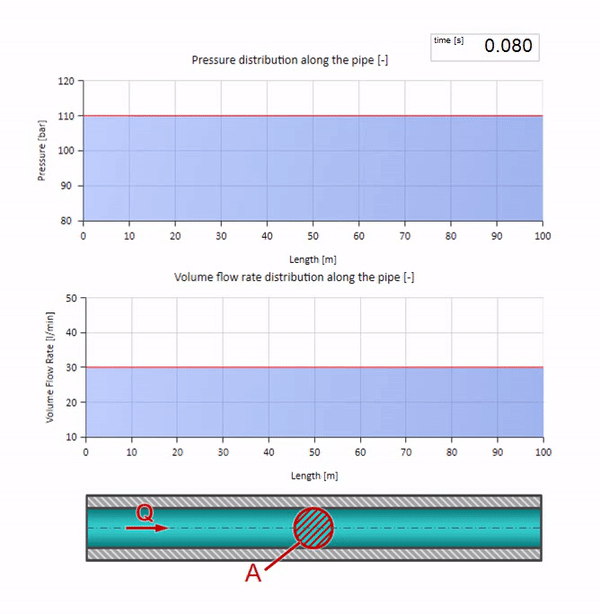
Si la presión en el extremo derecho aumenta, el fluido será inevitablemente inhibido por un diferencial negativo. Esto significa que la onda de aumento de presión que va contra el flujo conducirá a una disminución en la velocidad de flujo en una cantidad determinada nuevamente por la resistencia de la onda. Es decir, una ola de crecimiento de presión y flujo descendente se moverá a la derecha.
En una colisión, puede parecer que las ondas de flujo se reflejan entre sí y regresan. De hecho, simplemente se superponen. Este efecto también se llama interferencia:

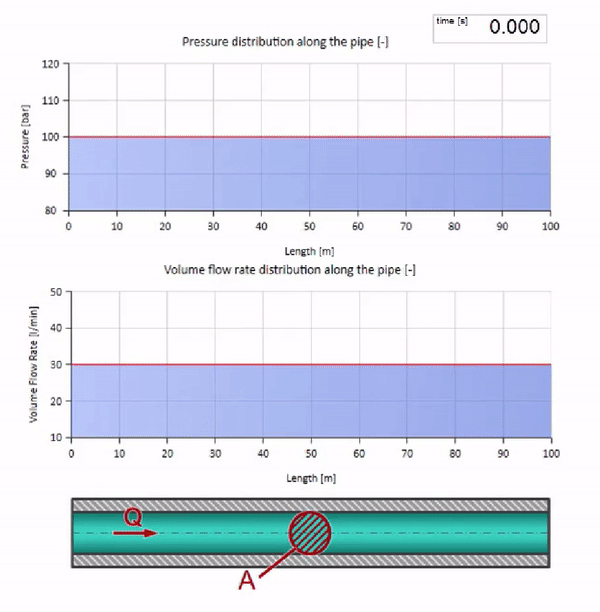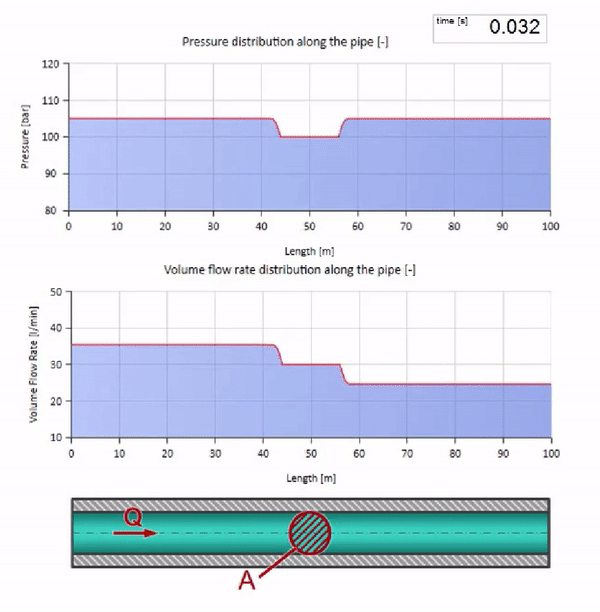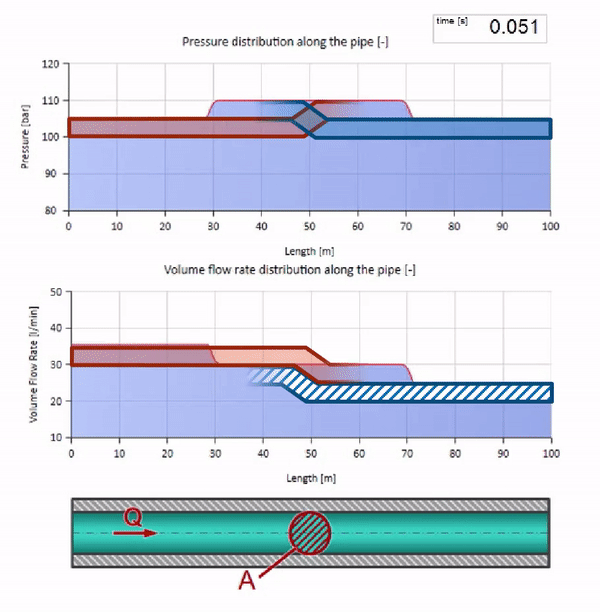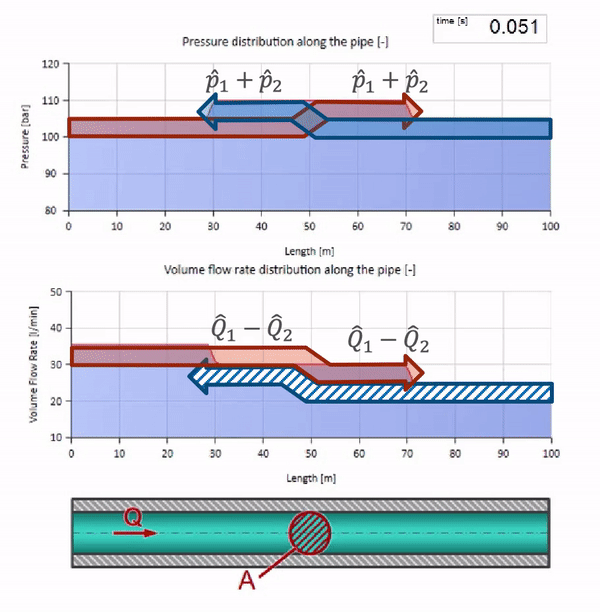
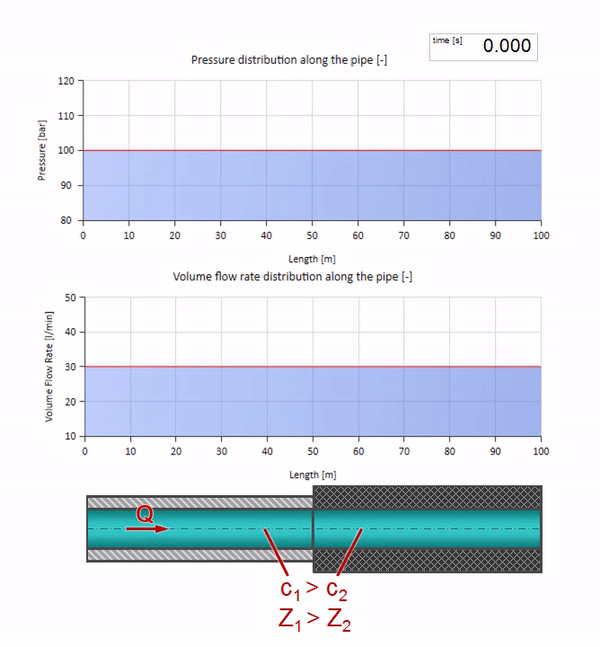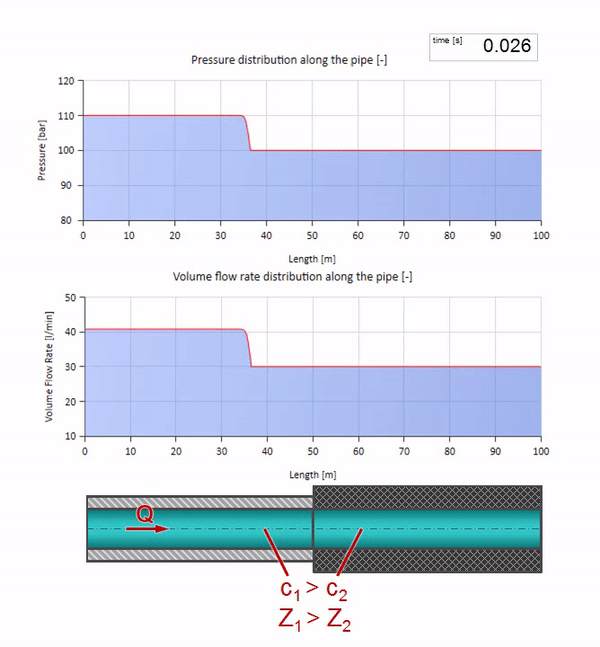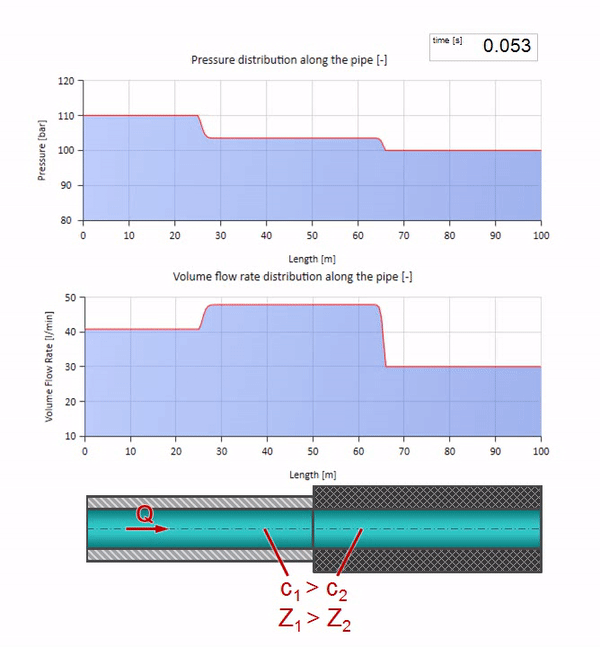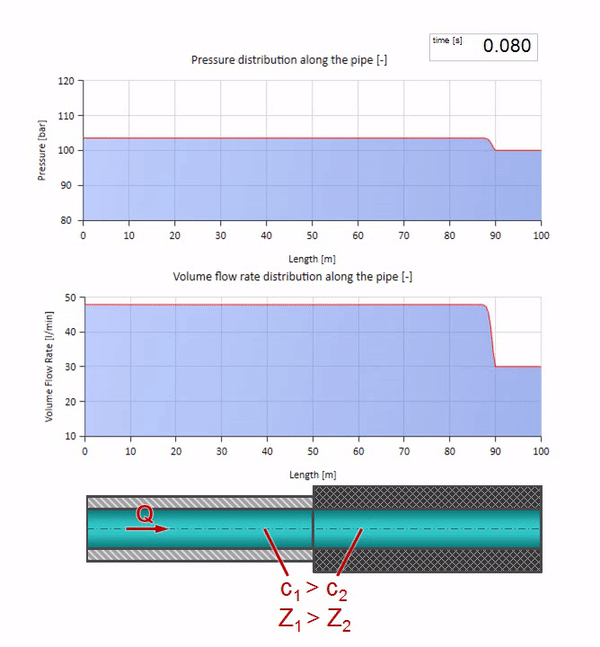
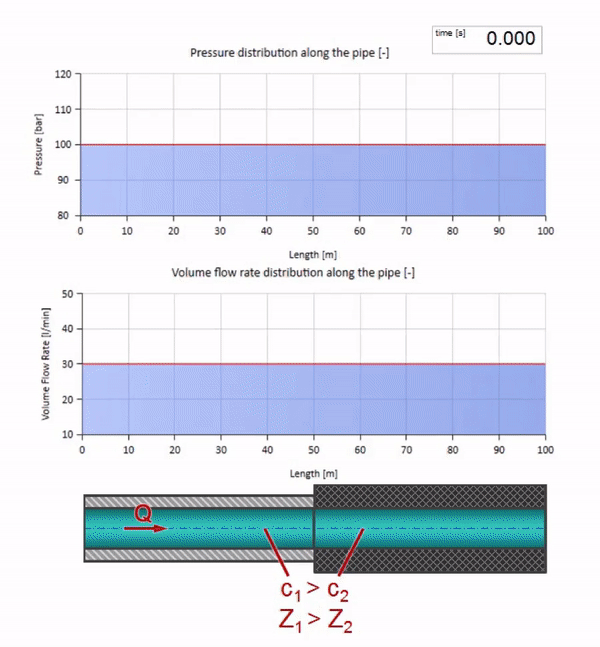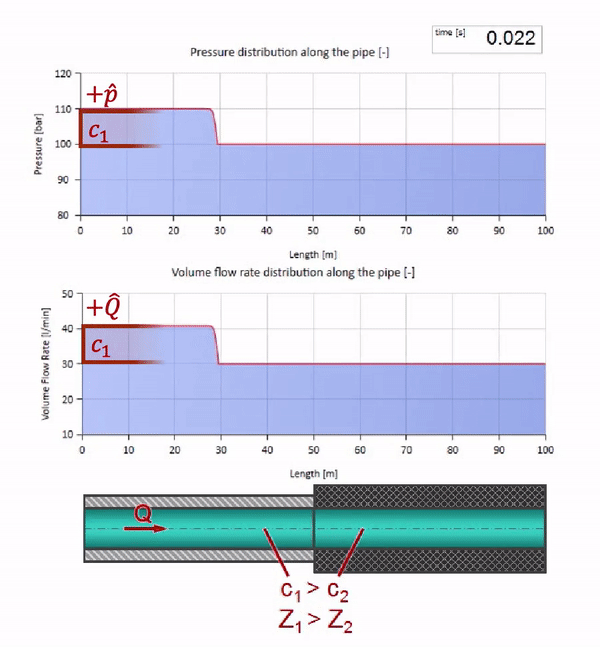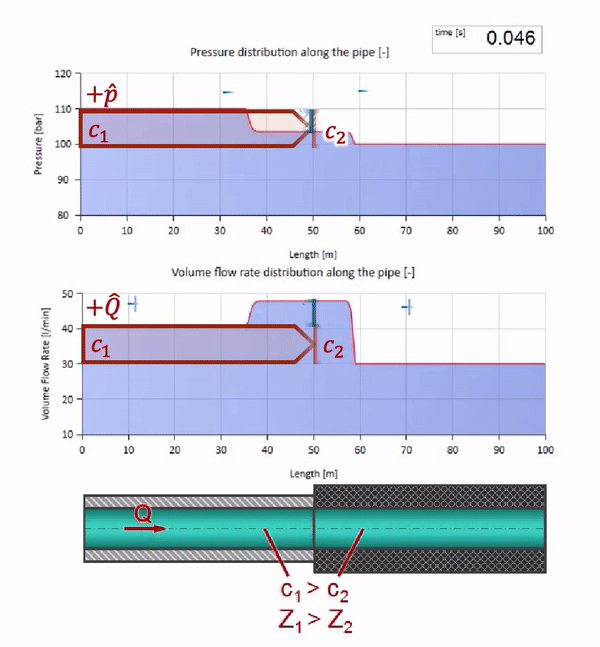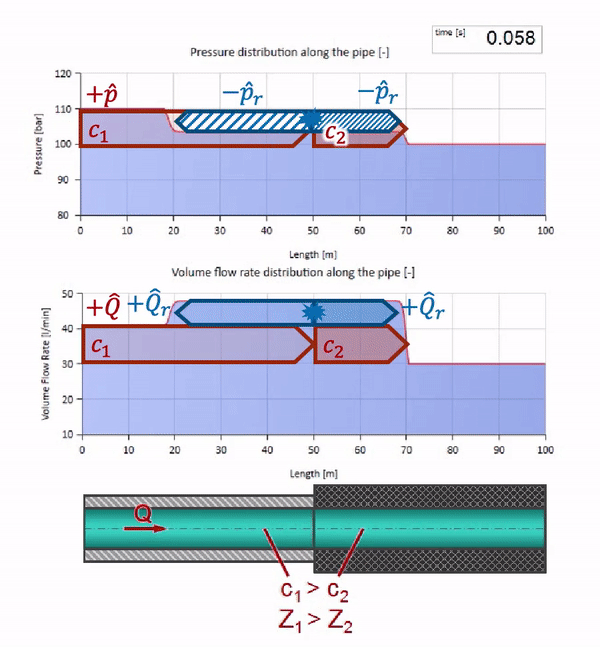
Ahora sabemos que cada tubería con un líquido tiene una propiedad como la resistencia a las olas. Es interesante ver qué pasará con la ola si el diámetro de una tubería en una determinada sección cambia drásticamente:

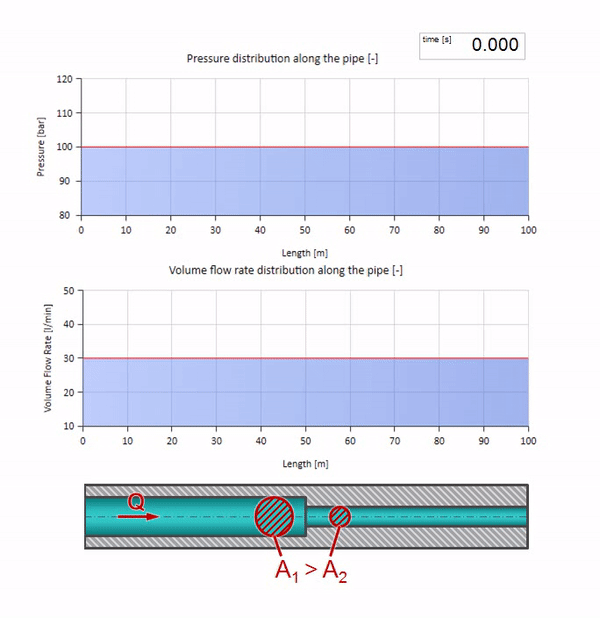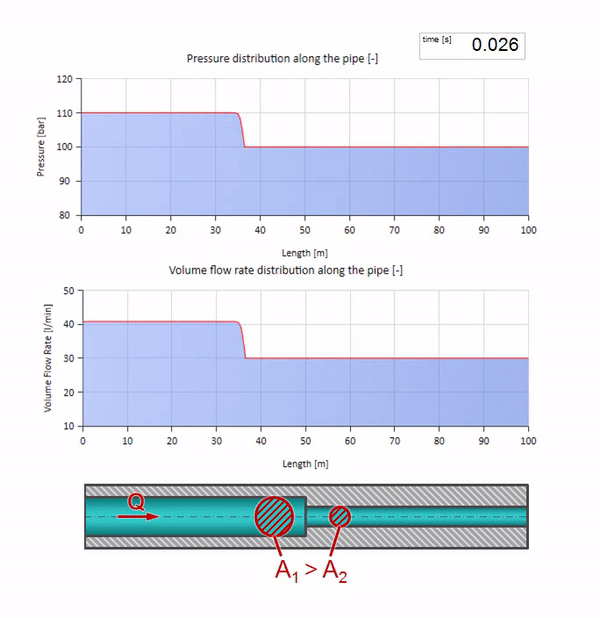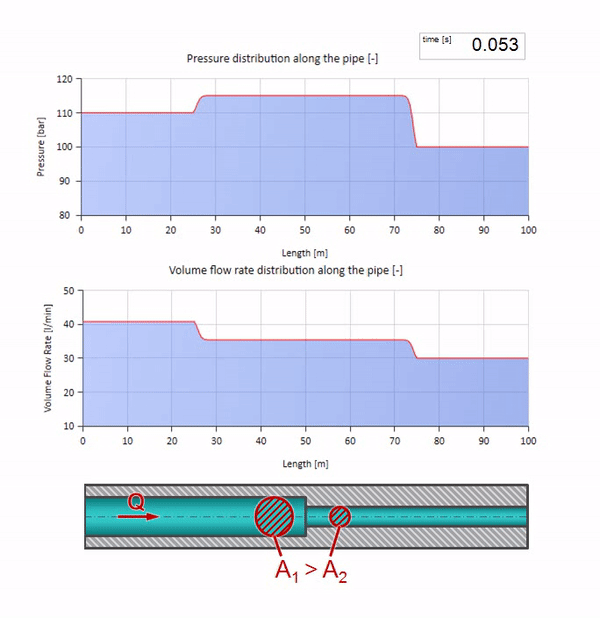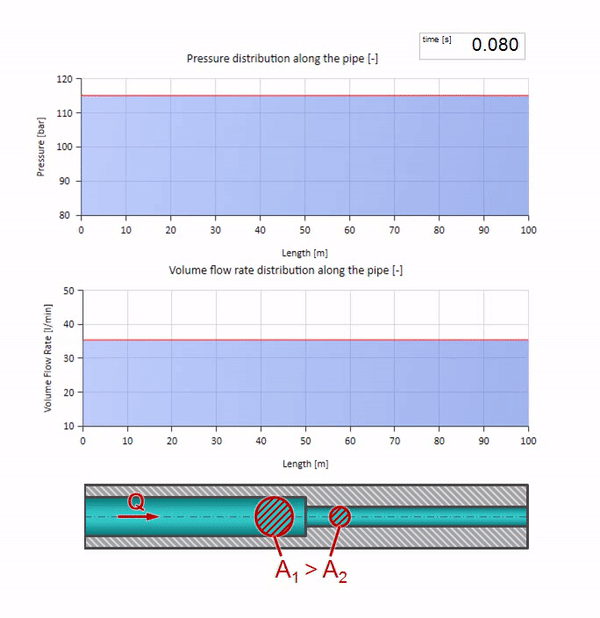
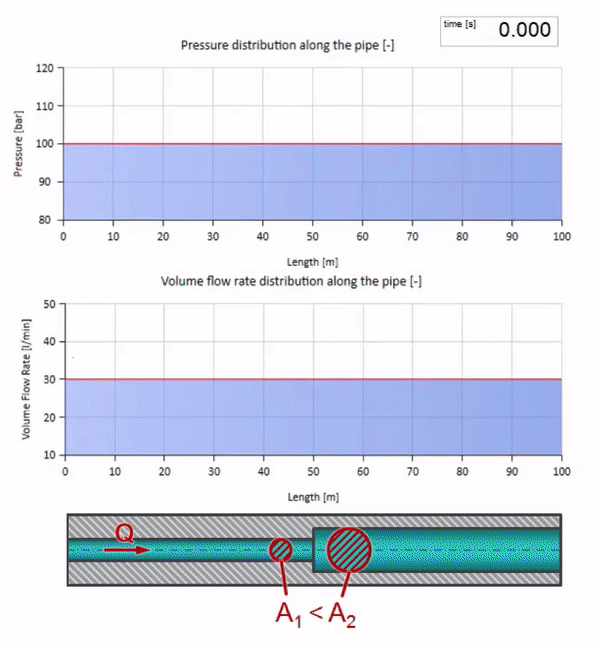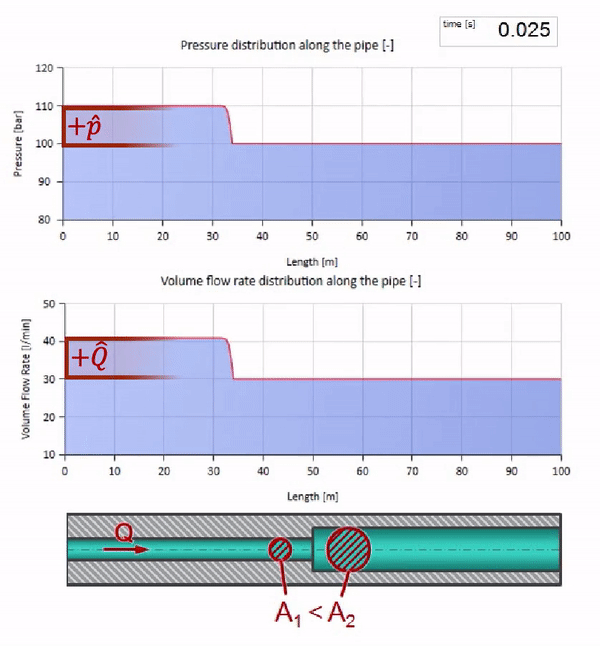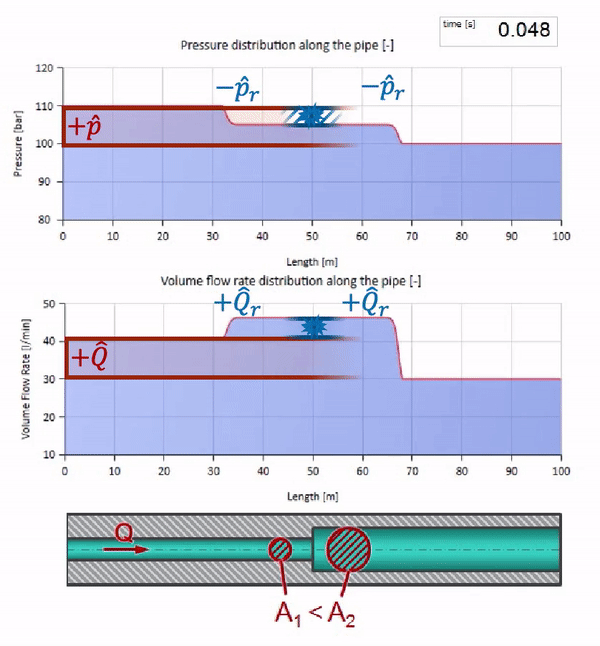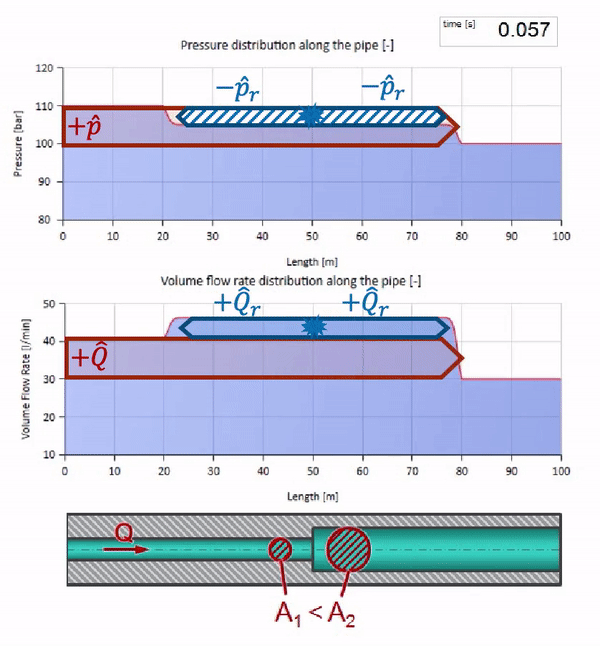
Antes de que la ola llegue a un lugar con una disminución en el diámetro de la tubería, por supuesto, no sucede nada interesante. Pero luego llega a una sección con una resistencia de onda más alta, lo que significa que la relación de la onda de presión a la onda de flujo debe ser mayor que en la sección de la tubería izquierda. Esto significa que la onda de presión debería aumentar y la velocidad de flujo debería disminuir. Al mismo tiempo, no queda nada para la ola excepto doblarse hacia la izquierda, mientras se mantienen valores iguales en la unión de las dos tuberías.

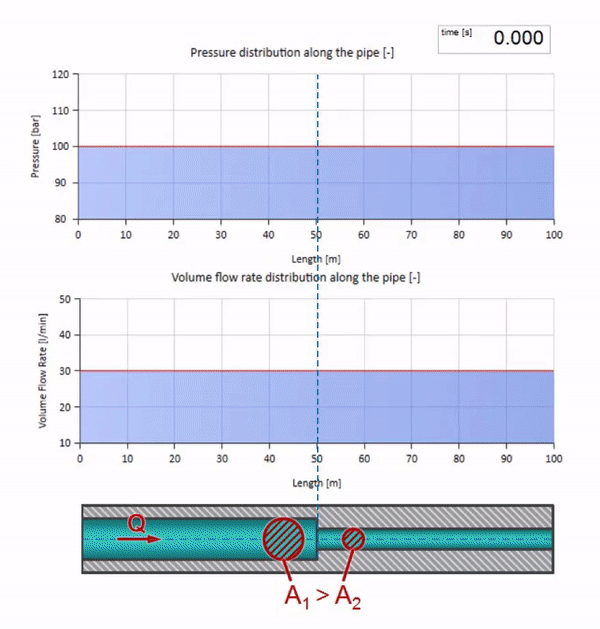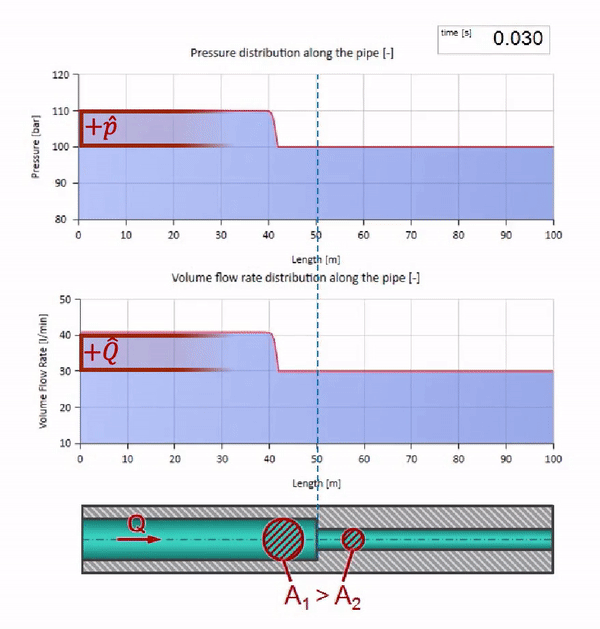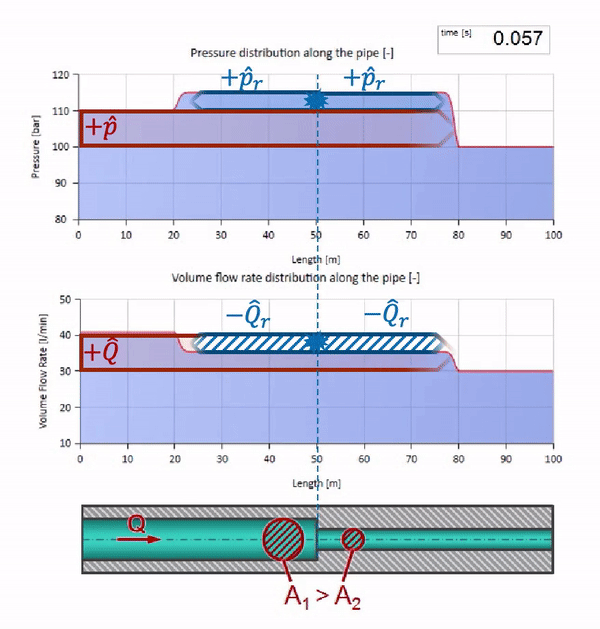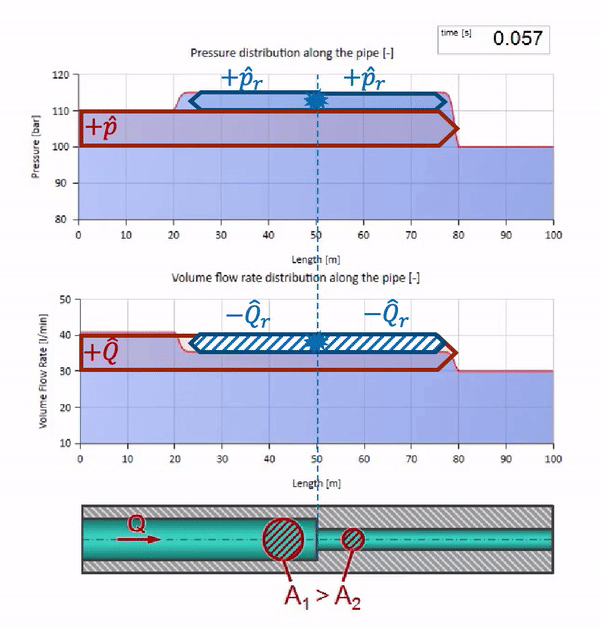
Para los cálculos, es conveniente usar el coeficiente de reflexión $$$r$ , que se considera a partir de las impedancias de onda de secciones individuales:

$$

$$r = \ frac {Z_2-Z_1} {Z_1 + Z_2}$$

Entonces la presión reflejada y las ondas de flujo se pueden calcular de la siguiente manera:

$$

$${\ widehat p} _r = r \; \ widehat p$$

$$

$${\ widehat Q} _r = - \ frac {\ displaystyle \; {\ widehat p} _r} {Z_1} = - r \; \ widehat Q$$

y estas ondas mismas se superpondrán de acuerdo con la ley de interferencia con la original.
Y se verá como una imagen del reflejo de una ola desde un sitio con menor resistencia a las olas:

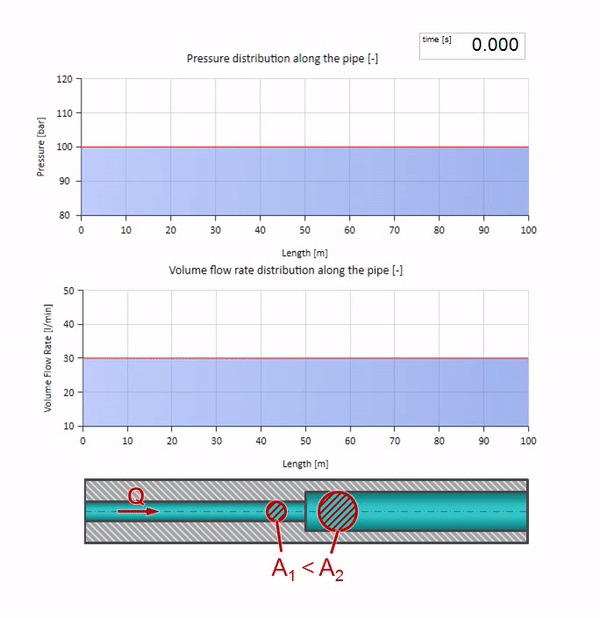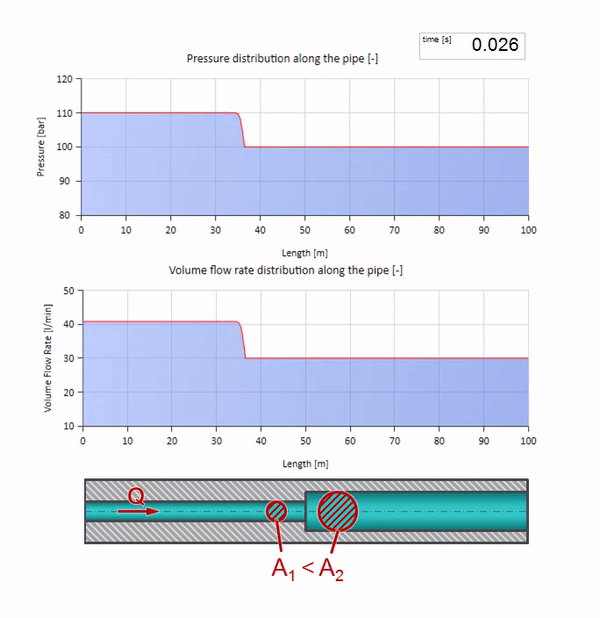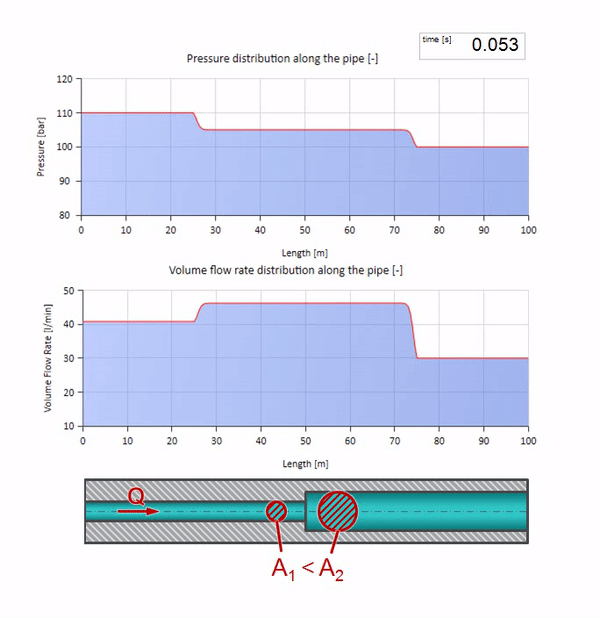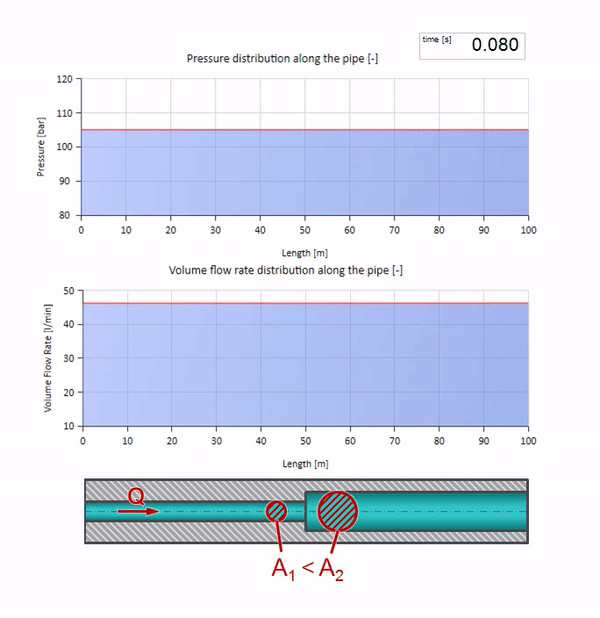
Se puede ver que esta vez el coeficiente de reflexión es negativo, lo que significa que la onda de presión después de la reflexión será menor, y el caudal, por el contrario, más.

Debe recordarse que la impedancia depende no solo del tamaño de la tubería, sino también de la velocidad local del sonido. Es decir Si tenemos una sección de tubería con una funda de goma en la que la velocidad del sonido es mucho menor, entonces la onda también se reflejará:

En primer lugar, inmediatamente llama la atención que la onda en la sección con la pared de goma de la tubería se mueve más lentamente. Y dado que la resistencia a las olas es menor, el resultado de la reflexión se parecerá al caso con la expansión de la tubería:

Ahora sería bueno considerar casos extremos con cero e infinitamente grandes valores de impedancia de onda. Esta será la salida de la tubería hacia el tanque con presión constante y el extremo cerrado, respectivamente. Dejaré estas animaciones sin comentarios:


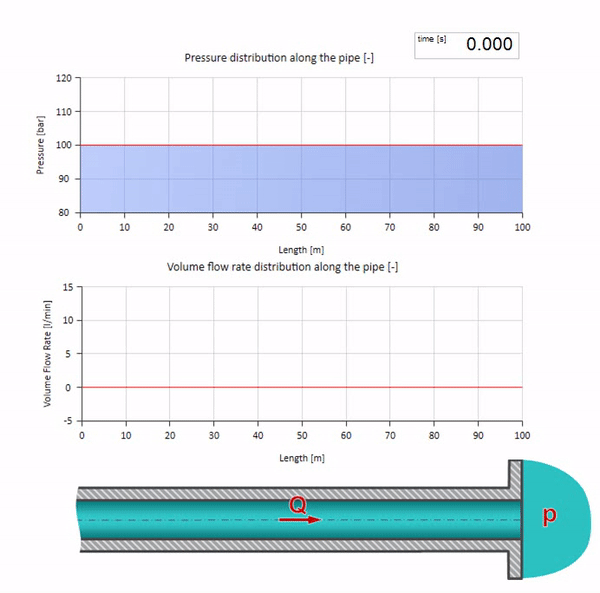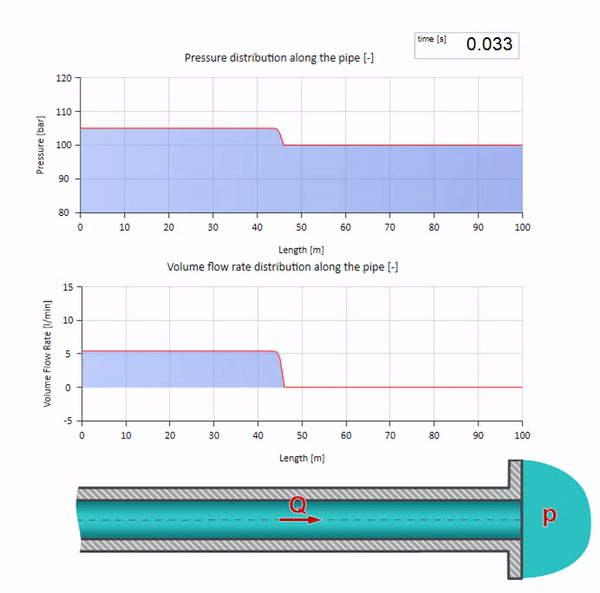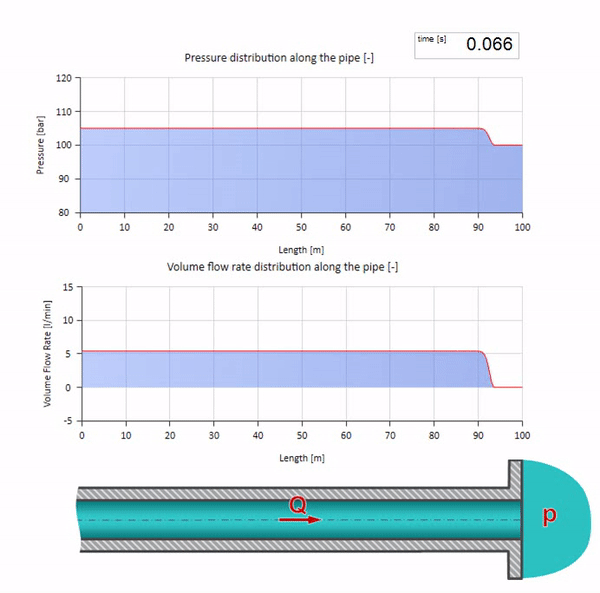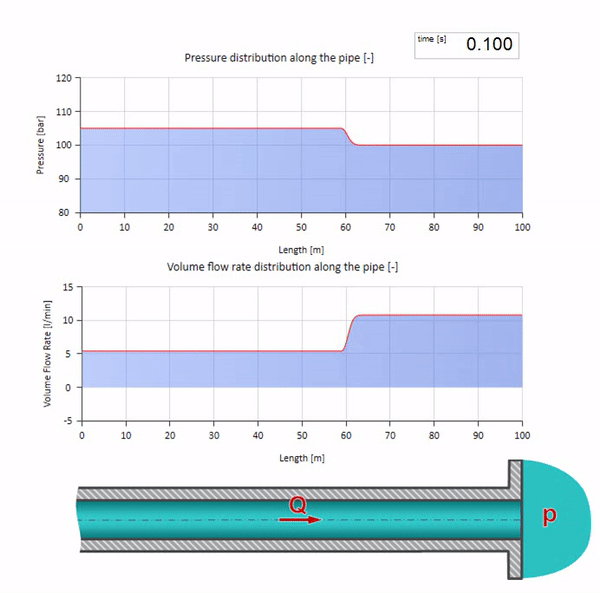
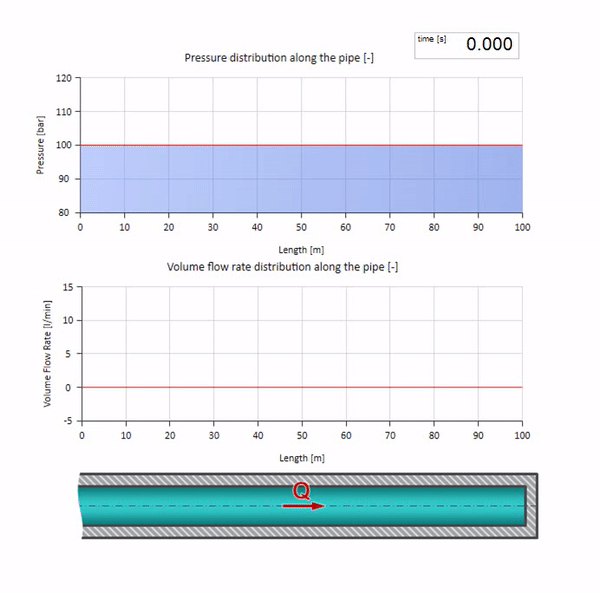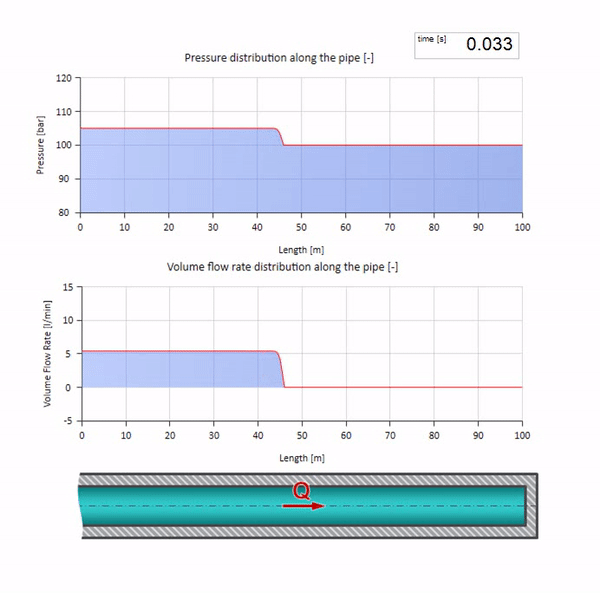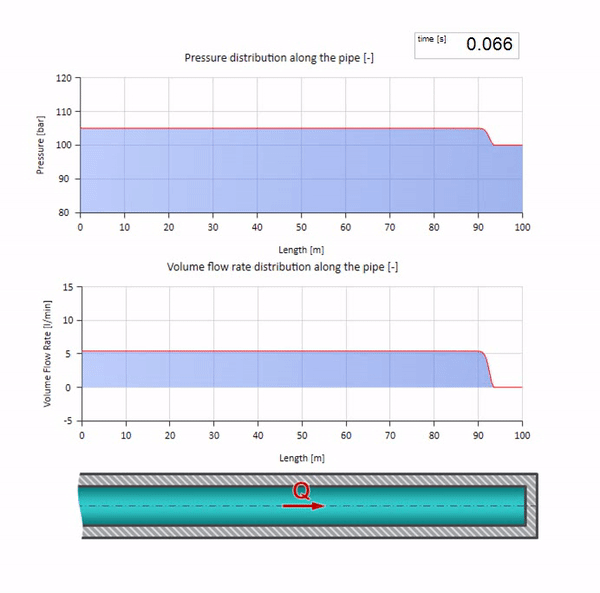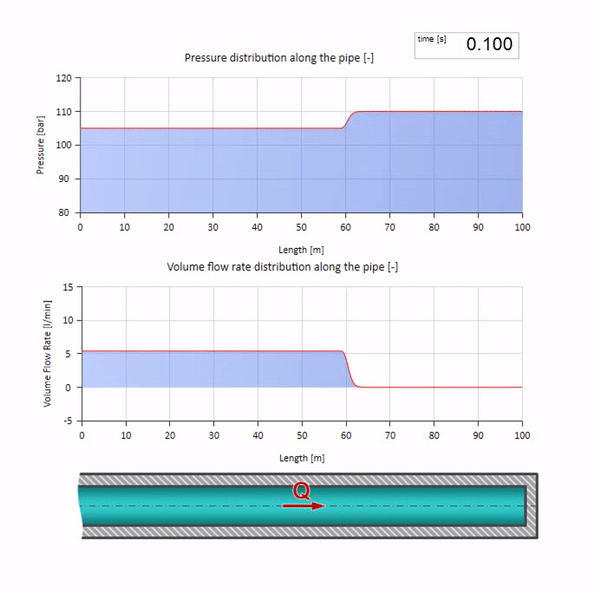
Bueno, si combinamos estos dos casos, obtenemos un choque hidráulico clásico:

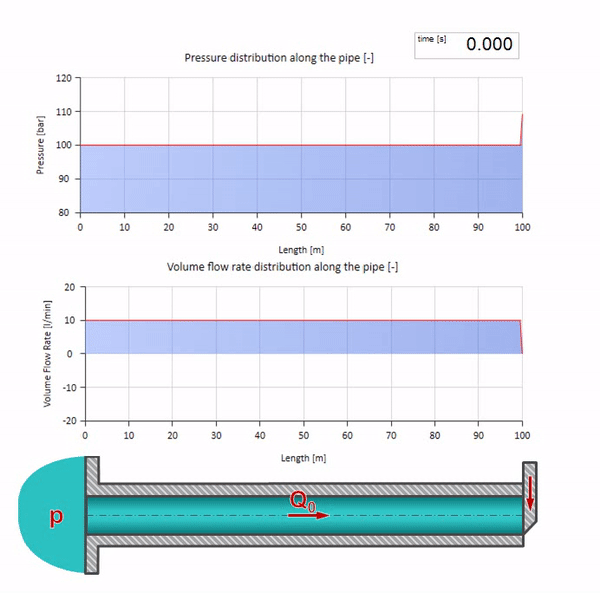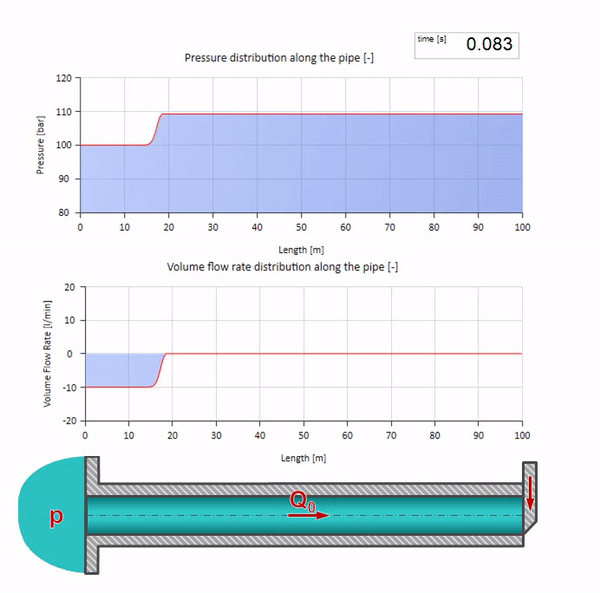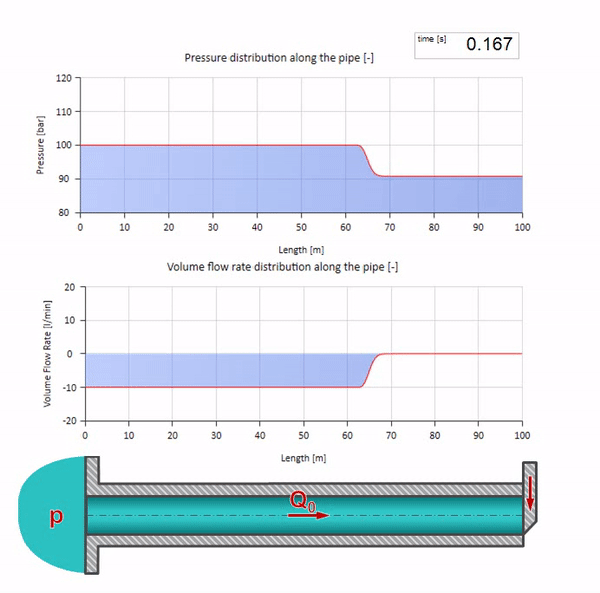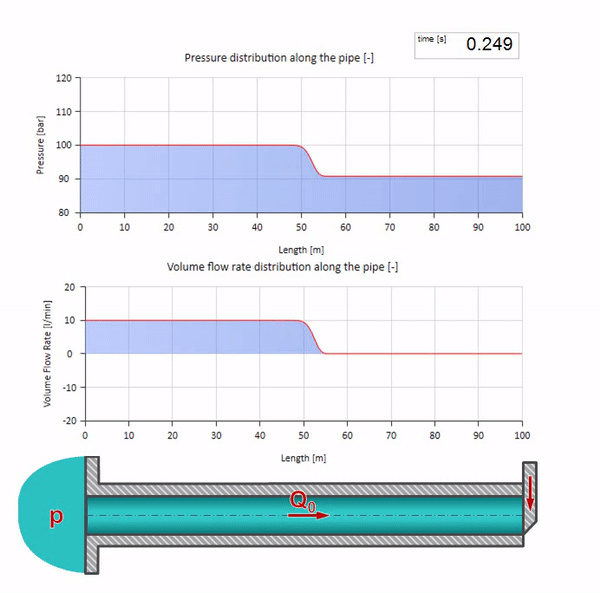
Aquí, en el momento inicial del tiempo, hay un valor de flujo que instantáneamente es igual a cero en el extremo derecho de la tubería (la válvula se cierra). Una ola de flujo descendente y presión creciente comienza a moverse hacia la izquierda. Estas ondas se reflejan desde el extremo derecho de la tubería con cero impedancia. En ausencia de fricción, este proceso será interminable.
Curiosamente, usando las fórmulas anteriores, podemos derivar la ecuación de Zhukovsky para el golpe de ariete:

$$

$$\ widehat p = Z_L \ widehat Q \;$$

Expresamos el caudal a través de la velocidad, asumiendo que cae de un valor dado a cero, y pintamos la impedancia de onda:

$$

$$\ widehat p = A \; v_0 \; \ frac {\ rho \; c} {\ A} = \ rho \; c \; v_0$$

Obtenemos el valor del salto de presión que ocurre cuando el obturador se cierra instantáneamente.

Notas

1. Me inspiró escribir un artículo del jefe de un libro de texto básico sobre hidráulica en el Departamento de Ingeniería Hidráulica de la Universidad Técnica Rin-Westfalia de Aquisgrán, donde, en mi opinión, los procesos en líneas hidráulicas se describen con mayor claridad (Grundlagen der Fluidtechnik Teil 1: Hydraulik, Hubertus Murrenhoff ISBN: 978-3-8440 -1223-1).
2. Se realizaron animaciones en el programa SimulationX, el cálculo se realizó por el método de características