Cómo crear mecánicas de juego confiables en Excel. Parte 2

En esta parte, resolveremos el problema de la colocación óptima de armas en el tanque, la disposición espacial de los teletransportadores en MMORPG y equilibraremos las batallas de las cuatro clases de personajes RPG.

Tareas de colocación de objetos

Las hojas de cálculo para esta parte se pueden descargar aquí: ( SuperTank ) ( teletransportadores, parte 1 ) ( teletransportadores, parte 2 )

SuperTank: ¡el problema está resuelto!

En el primer artículo de la serie, hablamos sobre un ejemplo de una tarea para un juego llamado SuperTank. En la segunda parte, nos familiarizamos con los conceptos básicos del modelado de decisiones y hablé sobre resolver un ejemplo simple usando la herramienta "Buscar soluciones" en Excel.

Ahora podemos aplicar el conocimiento adquirido en la segunda parte al problema de SuperTank, y demostrar que con su ayuda este problema puede resolverse fácil y rápidamente. Refresca tu memoria: SuperTank es un juego en el que puedes luchar en un tanque personalizado. El supertank se parece a esto:


Cada supertank puede tener cualquier cantidad de armas de cinco tipos diferentes:


Un supertank puede caber 50 toneladas de armas, y un jugador puede gastar 100 créditos. Además, el supertank tiene 3 "ranuras críticas", en las que se colocan pistolas especiales como MegaRocket y UltraLaser.

La hoja de cálculo para este ejemplo se puede descargar aquí .

El objetivo es recoger armas que maximicen el daño causado por el súper tanque, sin ir más allá de los límites de 50 toneladas, 100 créditos y 3 ranuras críticas. También suponemos que esta tabla contiene toda la información necesaria y que factores como el rango, la frecuencia y la precisión no son relevantes o ya se tienen en cuenta en el parámetro Daño del arma correspondiente.

Para optimizar este esquema, primero ingresamos estos datos en la hoja de cálculo. Justo debajo de él, agregaremos otra tabla, en la que habrá un conjunto de 5 celdas "cuantitativas" para indicar la cantidad de cada uno de los 5 tipos de armas.

Hasta que ingresemos un valor de 1 en estas celdas, solo para probar su trabajo, pero estas serán nuestras celdas de decisión: le pediremos a la herramienta Solver que encuentre los valores correctos para estas celdas. Es posible comprender que se trata de celdas de decisión en amarillo, porque seguimos las reglas de formato descritas en la segunda parte. A la derecha de las celdas "cuantitativas", agregaremos celdas de cálculo que multiplicarán los valores de cantidad en las celdas de decisión por los valores de Daño, Peso, Costo y Ranuras críticas de la tabla anterior. Por lo tanto, cada fila de esta tabla mostrará correctamente el daño, el peso, el precio y los espacios críticos necesarios para todas las armas usadas en todas las categorías de armas.


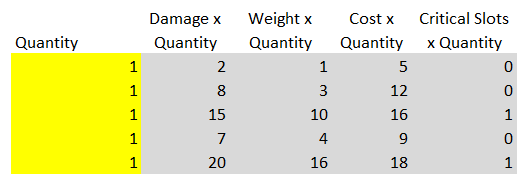
También crearemos una sección a continuación, que resumirá todos los valores de cantidad, peso, costo y ranuras críticas de la tabla anterior, y la compararemos con los valores máximos de peso, costo y ranuras críticas especificados en las condiciones de la tarea (50, 100 y 3, respectivamente).


De acuerdo con las reglas de formato de la segunda parte del artículo, las celdas azules en la parte superior son los criterios de las condiciones del problema. Las celdas grises son celdas de cálculo que representan el peso total, el costo y las ranuras críticas en función de la suma de la tabla de cantidades (es decir, los valores totales de las columnas Peso x Cantidad, Costo x Cantidad y Ranuras críticas x Cantidad). Finalmente, la celda naranja representa el daño total de nuestro súper tanque recibido en función del daño total de la columna Daño x Cantidad de la tabla anterior.

Antes de comenzar, hagamos que nuestra hoja de cálculo sea más fácil de usar. Aprovecharemos la oportunidad de Excel para asignar un nombre a cada celda y dar nombres claros a siete celdas en la última tabla de cálculo. Esto es opcional, pero a la larga hará que la hoja de cálculo se vea mucho más clara (por ejemplo, si en lugar de $ F $ 21 la celda se llamará MaxCriticalSlots). Para hacer esto, simplemente seleccionamos una celda y vamos al campo de entrada de nombre a la izquierda del campo de fórmula, e ingresamos un nuevo nombre.


Ahora, finalmente, vayamos a Excel Solver y busquemos una solución (vaya al lado derecho de la pestaña Datos y seleccione Solver. Si no lo ve, vaya a Opciones de Excel , seleccione la categoría Complementos ("Complementos"), asegúrese de que los Complementos de Excel estén seleccionados en la lista desplegable "Administrar", haga clic en Ir ("Ir ...") y asegúrese de La casilla de verificación Complemento Solver está seleccionada.

En el campo Establecer objetivo ("Optimizar la función objetivo") seleccionaremos la celda naranja del objetivo y luego haremos clic en el botón de radio Máx. ("Máximo"). En el campo Al cambiar las celdas variables, seleccione las celdas de decisión (celdas amarillas en la columna Cantidad de la segunda tabla). A continuación, haga clic en el botón Agregar para agregar las siguientes restricciones:

• Los valores de las celdas de decisión deben estar en el rango de 0 a algún máximo razonable (elegimos 50, aunque este es probablemente un valor límite mucho mayor que el necesario). También es necesario establecer cada celda de solución en una restricción "= entero", porque no podemos tener una parte fraccionaria del armamento, y Excel Solver considera que cada variable es un número real por defecto, a menos que se indique lo contrario.

• También debemos limitar los valores del costo total, el peso total y el número total de ranuras críticas a los valores de las condiciones del problema. La imagen del cuadro de diálogo muestra que ahora tienen nombres convenientes que hemos agregado a la tabla inferior, lo que hace que el cuadro de diálogo sea más fácil de leer.

Ahora hacemos clic en el botón Resolver ("Encontrar una solución") y después de una breve espera, Solver completará los valores de Cantidad, lo que nos dará lo siguiente:

• 1 ametralladora
• 3 cohetes
• 2 megacohetes
• 1 láser
• 1 UltraLaser

Todo esto nos da un daño total de 83 unidades y requiere exactamente 50 toneladas, 100 créditos y 3 ranuras críticas. Puede ver que la mejor solución no cambia con el tiempo de ejecución de Solver. Si restablece estos valores y realiza una segunda optimización, o va a Opciones y cambia la semilla, aún obtendremos los mismos valores. No podemos estar 100% seguros de que esta solución sea óptima, pero teniendo en cuenta el hecho de que Solver no logró mejorarla después de varios pases de optimización, es muy probable que sea un óptimo real, y no solo un máximo local.

¡El problema está resuelto!

Usos Adicionales

Lo bueno es que no solo resolvimos el problema mucho más rápido de lo que pudimos manejarlo manualmente, sino que también lo configuramos de tal manera que nos permite probar qué armas en el juego SuperTank serán más útiles con diferentes parámetros (peso, costo, ranuras críticas). Esto significa que podemos cambiar relativamente fácilmente el efecto de varios cambios en estos parámetros en el juego SuperTank, y si queremos agregar un nuevo modelo alternativo de super tanque que sea más liviano, más pesado o tenga un número diferente de ranuras críticas, entonces esto se puede hacer de manera muy simple.

Al cambiar todos estos parámetros, también podemos obtener una comprensión de la utilidad relativa de cada una de estas armas, y determinar rápidamente cuál es demasiado útil, no lo suficientemente útil, tiene un precio que no es adecuado para su peso y daño, y así sucesivamente.

Una vez más, el punto es que dicha herramienta nos permite buscar en el espacio de diseño mucho más rápido de lo que podríamos hacerlo manualmente. Nos brinda una oportunidad conveniente para evaluar el efecto de tales cambios para cualquier decisión de diseño incremental que podamos encontrar, ya sea cambiando los parámetros del arma o el súper tanque, agregando nuevas armas o modelos de súper tanques, así como agregando nuevos parámetros (digamos que el límite de tamaño está en metros cúbicos).

Para entender lo que quiero decir, vaya a la celda azul "Costo máximo" y cambie su valor de 100 a 99. Ahora ejecute Solver nuevamente y obtendrá un diseño de arma completamente diferente:

• 0 ametralladoras
• 2 cohetes
• 3 megacohetes
• 3 láseres
• 0 UltraLasers

Tal esquema da un índice de daño ligeramente más bajo (82 en lugar de 83), pero es radicalmente diferente del anterior.

Si establece el valor de Costo máximo en 101 o 102, y realiza el cálculo nuevamente, entonces existe la posibilidad de que obtengamos una configuración similar a la primera o que coincida con ella; Sea como fuere, el daño seguirá siendo igual a 83 (los esquemas pueden cambiar, porque en tales casos hay varios esquemas óptimos). Sin embargo, si establece el Costo máximo en 103, debería obtener lo siguiente:

• 1 ametralladora
• 4 cohetes
• 2 megacohetes
• 0 láseres
• 1 UltraLaser

Lo que aumenta el daño total a 84.

Esto es interesante: esta disposición de armas es muy diferente de las dos primeras.


Como puede ver, obtenemos un resultado inesperado: la elección óptima de armas en nuestro esquema depende en gran medida de los parámetros del súper tanque y puede variar significativamente incluso con pequeños cambios en estos parámetros. Además, esto nos proporciona todo tipo de información útil: los cinco tipos de armas son útiles en al menos dos de las tres configuraciones de súper tanque, y los Rockets y MegaRockets son obviamente útiles en los tres. Parece que esto nos dice que los cinco tipos de armas están bien equilibrados, es decir, son útiles entre sí y, al mismo tiempo, siguen siendo únicos.

Y como también puede observar, este modelado y optimización de soluciones nos brindan una excelente oportunidad para realizar búsquedas rápidamente en un vecindario local y volver a optimizarlas. Para algunos tipos de tareas, nos permitirá detectar estrategias dominantes y hazañas de jugadores que son difíciles o imposibles de encontrar de otra manera.

Teleportes - Agujeros de gusano

Si observa los dos últimos ejemplos (el ejemplo de las tasas impositivas en un juego estratégico y SuperTank), podría pensar que tales técnicas solo son aplicables en los casos en que los usuarios manejan números. ¡Pero estarás absolutamente equivocado! Como veremos, hay muchos ejemplos de cómo puede obtener los beneficios de optimizar elementos de diseño que no solo no se parecen a los números de los usuarios, sino que tampoco se parecen a ellos.

También puede pensar que el modelado de decisiones solo es aplicable a las decisiones que los jugadores pueden tomar en los juegos. Esto tampoco es cierto: en algunos casos pueden usarse para modelar con el fin de optimizar sus propias soluciones como diseñador.

Supongamos que está trabajando en un MMORPG espacial. Un día, su diseñador principal se le acerca con una ansiedad visible en su rostro. "Estamos completando un rediseño del sector Omega", dice. “Y tuvimos un problema. Planeamos agregar algunos teletransportadores de agujeros de gusano "en este segmento del mundo, pero no podemos acordar dónde colocarlos".

"¿Cuántos teletransportadores?", Preguntas.

“Todavía no lo sabemos. Probablemente tres, pero puede haber de dos a cuatro. Todavía no estamos seguros ". Luego te muestra un mapa que se ve así:


"¿Qué es esto?"

“Este es un mapa del sector Omega. O al menos los sistemas estelares que un jugador puede visitar en este cuadrante. Necesitamos determinar en qué células deben estar los agujeros de gusano ".

“Bueno, entonces, ¿y por qué reglas se colocan? ¿Es posible colocar el agujero de gusano en un cuadrante con el sistema estelar?

“Queremos que coloque los agujeros de gusano de tal manera que minimice la distancia desde cualquier sistema estelar al agujero de gusano más cercano. Y sí, puedes ponerlos en el mismo cuadrante que el sistema estelar; son solo pequeños teletransportadores que cuelgan en el espacio, por lo que se pueden colocar en cualquier lugar. Y recuerda que aún no hemos decidido cuántos debería haber, así que dame soluciones para 2, 3 y 4 agujeros de gusano ".

¿Cómo formular este problema y cómo resolverlo?

¡Optimizando teletransportadores!

Comencemos preparando células de solución. Denotamos los cuatro telepuertos como A, B, C y D. Sabemos que cada telepuerto no es más que las coordenadas (x, y) en el mapa estelar del sector Omega. También sabemos que necesitaremos alguna forma de indicar el número de teletransportes activos, por lo que agregaremos una celda que le permite establecer el número de teletransportes. Solo usamos el teletransporte D cuando se usan 4 agujeros de gusano, y C solo cuando tenemos 3 o más.


A continuación, prepararemos una tabla para calcular la distancia desde cada sistema estelar al teletransporte más cercano. Esta tabla se ve así:


El azul izquierdo muestra las coordenadas de cada sistema estelar en el mapa. Cada fila es un sistema estelar. Simplemente los transferimos del mapa del sector Omega, que nos dio el diseñador líder.

A la derecha, calculamos la distancia a cada uno de los cuatro teletransportadores. Esto es solo un teorema de Pitágoras. La distancia se calcula como la raíz cuadrada de las distancias horizontal y vertical entre el sistema estelar y el teletransporte:

= SQRT (($ B14-Ax) ^ 2 + ($ C14-Ay) ^ 2)

(No se preocupe, ¡prometo que esta es la matemática más difícil que encontraremos en la serie!)

Tomamos las coordenadas X e Y de cada sistema estelar de las celdas azules de la tabla de arriba, y las coordenadas X e Y de cada teletransporte (celdas con los nombres Ax y Ay para el teletransporte A en la función SQRT () que se muestra arriba) de las celdas de solución amarilla en la parte superior.

Finalmente, tomamos el mínimo de estos cuatro valores en la columna Dist to Closest, es decir, simplemente usamos la función MIN () para determinar el mínimo de cuatro valores a la izquierda. Luego resumimos la columna completa a continuación; la suma es la celda objetivo.

Es posible que haya notado que en la captura de pantalla anterior, todas las celdas están configuradas en Dist a D. ¿La razón es que estamos usando la celda “Número de teletransportadores? en la sección superior del modelo de solución, que le permite configurar el número de teletransportes que se tienen en cuenta. Si el número de teletransportadores es 2, entonces usamos el valor 99 en Dist a C y Dist a D, y si es 3, entonces el valor 99 se usa solo en la columna Dist a D. Por lo tanto, cada sistema estelar ignorará todos los teletransportadores innecesarios al calcular la distancia al telepuerto más cercano en el caso de 2 o 3 telepuertos.

Ahora lanzaremos Solver:


La celda objetivo es la suma en la parte inferior de la columna Dist. Más cercana. Tenga en cuenta que, a diferencia de otros ejemplos, aquí queremos usar el botón de opción "Para: Min" porque necesitamos una distancia mínima entre todos los sistemas estelares y teletransportadores, no un máximo.

A continuación, indicaremos ocho celdas amarillas para resolver las coordenadas X e Y de los agujeros de gusano A, B, C y D como celdas de las soluciones (al cambiar las celdas variables). En la sección de restricciones, limitaremos cada una de las coordenadas como un valor entero en el rango de 0 a 12. Tenga en cuenta que utilizamos una restricción entera para estas celdas de solución, porque queremos decir que el diseñador principal solo quiere saber en qué celda estará cada teletransporte, pero podemos omitir fácilmente esta restricción si el diseñador necesita coordenadas de material.

Si preguntamos por "Número de teletransportadores?" valores 2, 3 y 4, y secuencialmente lanzaremos Solver en cada valor, obtendremos las siguientes configuraciones:


Con esta información, podemos ir al diseñador líder y mostrarle las ubicaciones óptimas para la ubicación de cualquier número de teletransportadores en el rango de 2 a 4. Así es como se ven las ubicaciones óptimas de los "agujeros de gusano" para 2, 3 y 4 teletransportadores en el mapa (se muestra en verde).


La hoja de cálculo para este ejemplo se puede descargar desde aquí .

¿Hablé sobre el ninja?

"Increíble", dice el diseñador principal, pero ves sufrimiento en su rostro. “Uh, pero olvidé decirte que algunos de estos sistemas están habitados por ninja espacial. Y queremos que los sistemas con el ninja estén más lejos de los "agujeros de gusano" para que los jugadores no sientan una amenaza excesiva ".

"Wow. Esto está cambiando completamente el caso ".

"Bien. Además, en algunos sistemas estelares no hay una sino dos colonias, es decir, son dos veces más importantes que estar cerca de los teletransportadores. O es dos veces más importante ir más allá si se trata de un sistema con dos colonias de ninjas espaciales. Así es como se ve el mapa ahora: "


Él continúa: “Cada número negativo es una colonia de ninjas espaciales. El sistema con el número 2 contiene dos colonias humanas, y con el número -2 contiene dos colonias del ninja. ¿Me puede decir dónde colocar teletransportadores en este caso?

"Dime, al menos ya has decidido cuántos teletransportes habrá: ¿2, 3 o 4?", Preguntas sarcásticamente.

"Me temo que aún no".

Resolvemos teniendo en cuenta el ninja

Para resolver este problema, necesitamos agregar una nueva columna a la tabla que indique el peso de la tabla. Lo llamaremos el "multiplicador". Simplemente multiplicaremos este valor por el valor en la columna Dist a más cercano.

Cuando hacemos esto, Dist to Closest cambia ligeramente su significado. Ahora, esta no es la distancia al sistema estelar más cercano, porque para los sistemas estelares ninja el valor cambia en -1 veces. Se asemeja a "puntos" (puntaje) más generalizados, así que llamémosles así.


Por lo tanto, los puntos ahora indican el valor acumulativo. Al minimizarlo, hacemos que Solver se esfuerce por estar lo más cerca posible de los sistemas con colonias humanas y, al mismo tiempo, lo más lejos posible de los sistemas ninja poblados.

Ahora obtenemos los siguientes resultados:


Como puede ver, esto nos da la configuración de teletransportadores, en cada caso muy diferente de las versiones más simples sin un ninja.


La hoja de cálculo para esta versión extendida del ejemplo de teletransporte se puede descargar desde aquí .

Como puede ver, nuestro modelo de solución fue capaz de resolver muy rápidamente esta tarea no trivial, y podemos adaptarla a los requisitos cambiantes.

Esta tarea pertenece a la clase de tareas llamadas "tareas de asignación de objetos", que están muy bien estudiadas en el campo de la gestión operativa. Pero como puede ver, pueden usarse potencialmente en el diseño de juegos, así como en el diseño de niveles, y la solución es simple (si no trivial) en Excel.

Equilibrio de clase para peleas jugador contra jugador

La hoja de cálculo para esta parte se puede descargar desde aquí: enlace

Hojas de cálculo y simulaciones

En las tres partes anteriores de esta serie de artículos, nos presentamos el concepto de modelado y optimización de soluciones, así como la herramienta "Solver" del paquete Excel. Mostramos cómo se pueden usar para calcular las tasas impositivas óptimas de la ciudad en la estrategia 4X, para determinar la ubicación óptima de los teletransportadores en el juego espacial y para seleccionar el diseño de arma óptimo para la tarea de súper tanque descrita en la primera parte.

Surge una pregunta natural: ¿qué pasa con el equilibrio del juego? ¿Es posible aplicar técnicas similares a todo tipo de tareas complejas de equilibrio que se encuentran en muchos tipos diferentes de juegos, en particular, en estrategias, RPG y MMORPG?

La respuesta a esta pregunta es sí, por supuesto, pero con muchas reservas. Las hojas de cálculo en particular tienen muchas limitaciones, porque en la mayoría de los casos no triviales no describen con precisión el juego. Por lo tanto, será difícil para nosotros realizar un equilibrio confiable utilizando técnicas de optimización; Las verdaderas tareas de equilibrio de la gran mayoría de los juegos irán mucho más allá de lo que podemos modelar en una hoja de cálculo. La simulación del juego en sí misma suele ser demasiado complicada, tiene muchas "partes móviles" y a menudo se realiza en tiempo real, cuando tratamos de simular discretamente, podemos encontrar todo tipo de problemas.

Por lo tanto, si quisiéramos usar técnicas similares para equilibrar clases en MMORPG como WildStar o en juegos estratégicos comoAniquilación planetaria , para garantizar al menos cierta precisión y utilidad, tendríamos que integrarlos en la simulación del juego en sí.

Además, la verdad es que algunos aspectos del equilibrio no pueden automatizarse; Como explicamos en la primera parte del artículo, es imposible ajustar automáticamente la experiencia del juego.

Por lo tanto, lo mejor que podemos esperar es una demostración de un ejemplo simple que ilustre un enfoque general para tareas de este tipo: con un ejemplo simple en Excel, aprenderemos cómo abordar la formulación de este tipo de problemas de equilibrio y optimizarlos. Mostraremos que, al menos para un ejemplo de una batalla simple, Solver puede equilibrar varias clases de RPG entre sí. Luego puede utilizar esta estructura básica como base para resolver tales problemas de optimización con un esquema más complejo y más profundamente integrado en la simulación del juego.

Esperamos que con nosotros aprenda todos los trucos y vea lo que este simple ejemplo nos puede dar.

Desequilibrado

No existe una definición única y generalmente aceptada de la palabra "equilibrio". Tiene muchos significados, y la verdad generalmente depende del contexto del juego en cuestión. En diferentes condiciones, el equilibrio puede estar relacionado con la creación de varias clases de personajes para igualar sus capacidades en un juego de rol, con el número de fuerzas de los oponentes que luchan entre sí en un juego estratégico, o con el ajuste del costo de varias unidades o recursos de acuerdo con su utilidad.

La mejor definición de "equilibrio" generalmente depende de los objetivos de diseño del juego en cuestión, pero dado que estos objetivos pueden ser cualquiera, es imposible determinar a priori qué significa realmente el equilibrio para los juegos en general.

Algunos jugadores tienden a creer que equilibrarse en la batalla significa el mismo daño. Esto es especialmente cierto para los MMORPG, en los que los jugadores a menudo se quejan de que el daño por segundo (DPS) de una clase es demasiado pequeño o demasiado grande en relación con los demás.

Por supuesto, las clases no pueden ser balanceadas solo por DPS; es aceptable que una clase tenga un DPS más grande que otra, pero esto debe compensarse con otros factores que limitan la utilidad general de la clase, por ejemplo, una supervivencia reducida o menos DPS a largo plazo en comparación con el DPS a corto plazo.

Pequeño MMO

Imagine que estamos creando un nuevo proyecto, un juego de rol en línea multijugador masivo muy simplificado llamado "Tiny MMO". Como parte del desarrollo del diseño, nos esforzamos por equilibrar las cuatro clases para las peleas de jugador a jugador (PVP) para que las cuatro clases sean relativamente iguales en la batalla entre ellas, y que no haya una clase clara "mejor" o "peor" que Puedes luchar contra otras clases.

Aunque Tiny MMO es un juego en tiempo real, la acción de cada jugador dura exactamente 3 segundos, por lo que podemos discretizar presentándola como un juego por turnos en el que cada movimiento es una parte del juego de tres segundos.

Los jugadores en este juego pueden elegir una de las cuatro clases de personajes:

• Guerrero hace el mayor daño.
• Mage lanza hechizos desde la distancia y tiene el rango de ataque más largo de las cuatro clases.
• Healer (Healer) se trata automáticamente, restaurando para cada turno cierta parte de su salud.
• Bárbaro (Bárbaro) tiene la mayor salud

Esto es todo lo que sabemos sobre estas cuatro clases, y necesitamos establecer los parámetros iniciales de salud (HP), daño, curación y rango de ataques para las cuatro clases. Necesitamos equilibrarlos de tal manera que cada clase sea única y sus características difieran significativamente de todas las otras clases, pero de modo que cada clase resulte ser lo más "equilibrada" posible con respecto a las otras tres.

En otras palabras, nos esforzamos por optimizar la siguiente tabla:


Si bien utilizamos valores temporales y suponemos que cada clase comienza con 50 HP, causa 10 daños por turno, cura 0 HP por turno y tiene un alcance de ataque de 40 metros. Cada personaje se mueve a una velocidad de 10 metros por turno. Como el diseño indica que las cuatro clases de caracteres pueden moverse a la misma velocidad, consideraremos este valor constante y no ingresaremos la velocidad de movimiento en la tabla de variables de decisión.

Obviamente, este es un caso de estudio con un modelo de daño muy simplificado. Este es un valor promedio continuo de daño por segundo, que ignora la diferencia entre el daño del pulso y el daño a largo plazo, así como el maná y otras mecánicas que modifican las habilidades de ataque de las clases. Solo tendremos un tipo de daño, lo cual es bastante poco realista, porque la mayoría de las clases tienen docenas de tipos de daño, y necesitaremos implementar un sistema de IA que seleccione el ataque en cada turno. Además, en la mayoría de los juegos, el daño tiene un elemento de aleatoriedad, pero por ahora lo omitiremos y asumiremos que la variabilidad del daño no es tan grande como para afectar significativamente el resultado de la batalla entre las dos clases.

Por supuesto, cualquier balance realizado en Excel es poco probable que sea ideal o consistente con el balance final del juego; ella tendrá que pasar por muchas iteraciones de pruebas de juego. Pero si nos tomamos una o dos horas para obtener una buena primera opción para nuestro juego en Excel, entonces al menos es mucho más probable que nos acerquemos a los parámetros cualitativos del saldo inicial, lo que nos acercará al saldo final que queremos obtener.

Mesa de la victoria

Necesitamos equilibrar cuatro clases entre sí en una batalla uno a uno. Como solo tenemos 4 clases (Guerrero, Mago, Sanador y Bárbaro), hay 6 combinaciones posibles de diferentes clases:

• Guerrero - Mago
• Guerrero - Sanador
• Guerrero - Bárbaro
• Mago - Sanador
• Mago - Bárbaro
• Sanador - Bárbaro

Este equilibrio puede ser bastante complicado. Incluso en nuestro caso bastante simple con cuatro clases, tenemos seis relaciones entre clases, así como podemos dibujar seis líneas entre cuatro puntos de un cuadrado.


Cada vez que deseamos realizar incluso un pequeño cambio en uno de los parámetros de cualquiera de las clases, este cambio también afectará el equilibrio PvP entre este par de clases y las otras dos clases. Esta interconexión de la ley de poder solo crecerá con un aumento en el número de clases, y las decisiones sobre el equilibrio de PvP entre cualquier par de clases hechas "en el vacío", sin tener en cuenta todas las demás interacciones, pueden volverse muy peligrosas.

Idealmente, nos gustaría crear algún tipo de tabla de victoriacomo el que se muestra a continuación. Si podemos simular una batalla entre cada uno de estos 6 pares en una hoja de cálculo, podremos generar una determinada variable de "puntos" para cada uno de los 6 pares. Cuantos más puntos, mejor, entonces podemos combinar los seis puntos para generar una función de objetivo.


Tenga en cuenta que en la tabla anterior, las celdas a lo largo de las diagonales son cero, porque denotan pares de la misma clase que se equilibrarán por definición. Además, las celdas en la esquina superior derecha también son cero, porque denotan exactamente los mismos pares que en las celdas en la esquina inferior izquierda.

Ahora preparemos el modelo para la batalla entre dos clases diferentes.

"Simulador de batalla"

Organizaremos cada par de clases a una distancia de 100 metros entre sí. Cada personaje tiene 3 segundos para atacar, por lo que podemos imaginar esto como una simulación por turnos en la que cada "movimiento" significa 3 segundos. En cada "movimiento", cada personaje ataca al otro, si está dentro del alcance del ataque, o continúa moviéndose para reducir la distancia.

La simulación se ve así:


Arriba hay un par de personajes que entraron en la batalla: en este caso, Mage (clase 1) y Healer (clase 2). La columna izquierda muestra la distancia actual entre los dos caracteres simulados.

Para cada personaje, las columnas serán:

• Max Range : , . .
• Healing : , .
• HP : . HP , . , .
• Damage : , , . , 0.
• Los ataques? : Esta columna verifica si el personaje está dentro del rango de ataque. Si es así, esto significará que el personaje está atacando en el turno actual; si no, el personaje se acerca para alcanzar a otro personaje.

Por lo tanto, ambos personajes comienzan a moverse uno hacia el otro, y luego atacan hasta que cualquiera de ellos o ambos mueren. Cada personaje se mueve cada 3 segundos 5 metros (5 metros por "turno"). Cuando ambos personajes se mueven el uno hacia el otro, el Rango cambiará en cada turno en 10 unidades, y en 5 unidades si solo uno de ellos se mueve. El juego en sí está estructurado para que ambos personajes puedan comenzar a moverse simultáneamente, después de lo cual se permite el movimiento al mismo tiempo, por lo que es posible que ambos personajes puedan morir al mismo tiempo.

Luego, necesitamos establecer la puntuación para esta tabla y generar un valor numérico que indique cuán "buena" fue la batalla; en otras palabras, qué tan cerca estamos de alcanzar nuestros objetivos de diseño.

Obviamente, queremos que ambos personajes estén muertos al final de la batalla, o al menos estén lo más cerca posible de la muerte. Si la batalla es equilibrada, ambas clases de lucha deberían minimizar la salud del enemigo al final de la batalla.

Sin embargo, esto solo no es suficiente. Si organizamos la puntuación de esta manera, ¡entonces el optimizador simplemente maximizará los valores de daño para que ambos personajes se maten instantáneamente! (Si tiene curiosidad, intente cambiar la hoja de cálculo adjunta al artículo para verlo usted mismo). Obviamente, no luchamos por la muerte instantánea: necesitamos que ambos personajes estén muertos o casi muertos al final de la batalla, pero al mismo tiempo queremos que la pelea dure un tiempo razonable.

En otras palabras, no solo nos esforzamos por garantizar un equilibrio relativamente igual de todas las clases entre sí; También queremos hacer que el balance sea interesante , incluida la lucha que dura una cantidad de tiempo adecuada.

Para generar tal estimación de saldo, necesitamos crear varias celdas a la derecha de cada tabla. Duración indica la duración de la batalla; ella cuenta el número de filas en la tabla en la que ambos personajes todavía están vivos. Total HP calcula los puntos de golpe totales de los dos personajes supervivientes. Idealmente, debería ser 0, es decir, para cuando la batalla termine, ambos personajes están muriendo.


Y finalmente, Score combina la duración y la cantidad total de puntos de golpe en el formulario (Duración / (1 + HP total)). Observe que agregamos 1 al divisor, porque Total HP podría ser 0, y en ese caso obtendríamos un error de división por cero. De esta forma, podemos garantizar que recompensemos al optimizador por encontrar la duración máxima de la batalla y el valor mínimo de la suma de los puntos de golpe.

(Tenga en cuenta que dado que tenemos 17 líneas en cada "simulación" de combate de clase a clase. Esto significa que esencialmente tomamos una decisión de diseño de que la pelea debería durar alrededor de 17 rondas. Si queremos que la pelea sea más corta o durante más tiempo, puede cambiar el número de filas, editar la fórmula para calcular el puntaje y realizar una segunda optimización en consecuencia).

Finalmente, tomamos estos seis valores de Puntuación (uno para cada tabla) y los usamos en la Tabla de Victoria anterior para mostrar los resultados de la batalla entre cada par de clases.

Simplemente puede resumir estos seis valores de puntaje y usar el resultado como el valor de puntaje final. Sin embargo, si hacemos esto, entonces Solver con una alta probabilidad no podrá encontrar un buen equilibrio entre las calificaciones más altas y más bajas para las peleas individuales, y también recibirá calificaciones muy altas para algunos pares de clases y calificaciones bajas para otros. Esto no es lo que queremos: necesitamos que todas las calificaciones sean altas y nos esforzamos por elevarlas todas. Para solucionar esto, multiplicamos la suma de las calificaciones por la calificación más pequeña en el grupo (usando la función MIN () de Excel) para que Solver se enfoque en las calificaciones con el valor más bajo.

Agregar restricciones

Aún no hemos terminado. Si optimiza un modelo de solución con los parámetros actuales, lo más probable es que las clases no se configuren correctamente; de ​​hecho, es muy probable que el modelo escriba los mismos valores de HP, Daño, Curación y Rango en la tabla de variables de decisión.

Y, por supuesto, queremos que cada clase tenga su propia personalidad. Necesitamos que Warrior haga el mayor daño, Mage tiene el rango más grande, Healer tiene el valor de curación máximo y Barbarian tiene el HP más alto. También queremos que estas diferencias no sean demasiado pequeñas, necesitamos que estas clases sean muy diferentes entre sí.

Para hacer esto, crearemos una pequeña tabla de restricciones. Esta tabla garantiza que cada una de las cuatro clases tendrá un atributo correspondiente, y luego dará una puntuación de 0 o 1, dependiendo de si se cumple la condición de restricción.


La tabla Diferencia mínima de la derecha muestra la diferencia mínima de cada atributo de la clase en relación con todas las demás clases. En otras palabras, Warrior debe tener al menos 4 HP más de daño que todas las demás clases, Mage debe tener un rango de ataque de al menos 10 más, y así sucesivamente.

Ahora que hemos agregado estas restricciones especiales, ¡es hora de optimizar!

Busca soluciones

Ahora podemos ejecutar la herramienta Solver ("Encontrar soluciones") integrada en Excel para tratar de optimizar los parámetros iniciales. Como celda objetivo, seleccionaremos la celda Puntuación, que combina los resultados de los seis torneos. Establecimos las variables de decisión para incluir las 16 celdas en la tabla amarilla de variables de decisión que creamos al principio.

También establecemos las restricciones (en el campo Sujeto a restricciones) de la siguiente manera:

• Todas las celdas de decisión deben ser enteras con un valor mínimo de 0.
• Todas las celdas de la columna HP deben tener un valor máximo de 200 y un mínimo de 30.
• Todas las celdas en la columna Daño tienen un valor máximo de 20.
• Todas las celdas en la columna Curación tienen un valor máximo de 15.
• Todas las celdas en la columna Rango tienen un valor máximo de 100.
• Además, las cuatro celdas en la sección Restricciones especiales deben establecerse en 1 para satisfacer sus condiciones especiales.

Finalmente, configure el Método de resolución en Evolutivo y ejecute Solver. Tenga en cuenta que, dado que se trata de un algoritmo evolutivo, existe la posibilidad de mejorar la solución encontrada durante la segunda o tercera ejecución de Solver, o después de configurar los parámetros (botón Opciones) para la optimización evolutiva.

Como resultado, deberíamos obtener algo similar:


... y como por arte de magia, Solver nos dio una buena configuración de equilibrio inicial.

Como puedes ver, Warrior ahora hace el mayor daño, Mage tiene el rango más grande, Healer cura mejor y Barbarian tiene la mayor cantidad de HP. Además, puedes ver los resultados de los torneos individuales "clase contra clase" y ver cómo las clases se mostraron en la batalla entre ellas; Como puede ver, la mayoría de ellos están equilibrados de manera muy uniforme: al final de la batalla, ambas clases están muriendo, o una de ellas apenas sobrevive. Además, todos los torneos duran lo suficiente, ninguna de las clases puede "patear" a la otra.

No está mal para unas pocas horas de trabajo, ¿verdad?

Conclusión

En este ejemplo, creamos una tarea de equilibrio simple y demostramos que, de hecho, podemos resolverla con la ayuda de la simulación y la optimización. Aunque es obvio que este es un ejemplo simple, nos muestra el poder de las técnicas de modelado y la optimización de decisiones. Además, puede convertirse en una fuente de inspiración que se puede utilizar en herramientas de equilibrio más complejas, estrechamente integradas en la simulación del juego. Esperamos que pueda usar este ejemplo como guía para formular tales tareas en la práctica.

En las siguientes dos partes de la serie, profundizaremos en el área de tareas de asignación, que está asociada con la selección de asignaciones óptimas de dos o más conjuntos de entidades. Mostraremos cómo resolver este tipo de problemas y demostraremos cómo usamos este enfoque para crear el diseño de la torre en nuestro juego de estrategia para iOS / Android City Conquest .