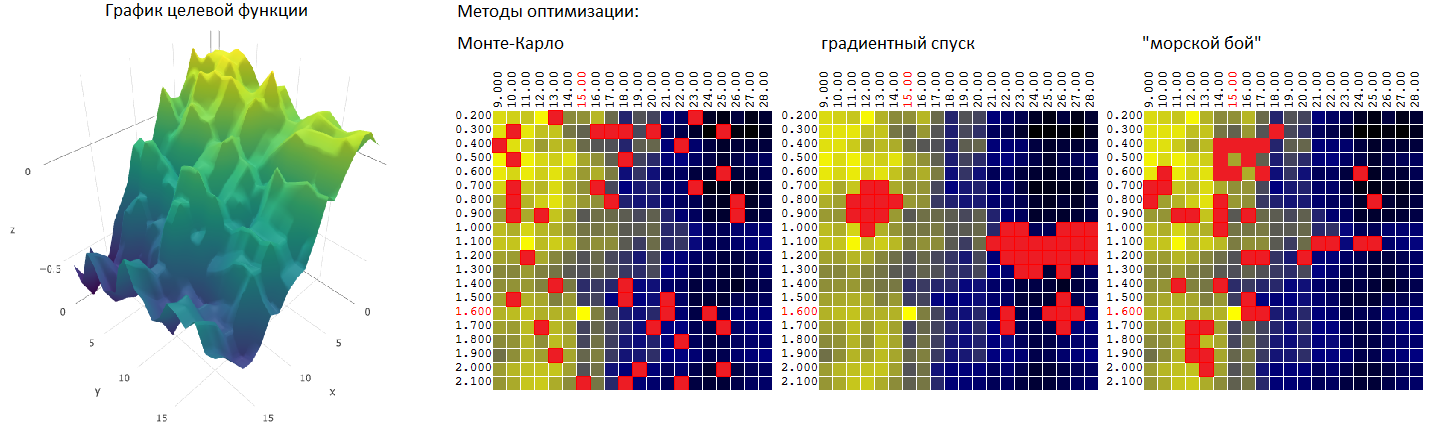
Leí un libro autorizado sobre estrategias comerciales y escribí mi robot comercial. Para mi sorpresa, el robot no trae millones, incluso comerciando virtualmente. La razón es obvia: un robot, como un automóvil de carreras, necesita ser "ajustado" para seleccionar parámetros adaptados a un mercado específico, un período de tiempo específico.
Dado que el robot tiene suficientes configuraciones, itera sobre todas sus combinaciones posibles en busca de la mejor tarea, que consume demasiado tiempo. En un momento, al resolver el problema de optimización, no encontré una elección razonable del algoritmo de búsqueda para el vector cuasi óptimo de los parámetros del robot comercial. Por lo tanto, decidí comparar independientemente varios algoritmos ...
Breve declaración del problema de optimización.
Tenemos un algoritmo comercial. Datos de entrada: historial de precios del intervalo por hora durante 1 año de observación. Datos de salida - P - ganancia o pérdida, valor escalar.
El algoritmo de negociación tiene 4 parámetros configurables:
- Mf es el período de la media móvil "rápida",
- Ms período de la media móvil "lenta"
- T - TakeProfit, el nivel de beneficio objetivo para cada transacción individual,
- S - StopLoss, el nivel de pérdida objetivo para cada transacción individual.
Asignamos un rango y un paso de cambio fijo a cada uno de los parámetros, un total de
20 valores para cada uno de los parámetros.
Por lo tanto, podemos buscar el beneficio máximo (P) para un parámetro en una matriz de datos de entrada:
- variando un parámetro, por ejemplo, P = f (Ms), produciendo hasta 20 backtests ,
- variando dos parámetros, por ejemplo, P = f (Ms, T), produciendo hasta 20 * 20 = 400 backtests,
- variando tres parámetros, por ejemplo, P = f (Mf, Ms, T), produciendo hasta 20 * 20 * 20 = 8,000 backtests,
- variando cada uno de los parámetros, P = f (Mf, Ms, T, S) y produciendo hasta 20 ^ 4 = 160,000 backtests.
Sin embargo, para la mayoría de los algoritmos de negociación, lleva varias órdenes de magnitud más tiempo realizar una sola prueba. Lo que nos lleva a la tarea de encontrar un vector de parámetros casi óptimo sin la necesidad de iterar sobre todo el conjunto de combinaciones posibles.
detalles sobre el comercio y los robots comercialesOperar en la bolsa de valores, apostar en el centro de operaciones de Forex, apuestas locas sobre "opciones binarias", especulación con criptomonedas, una especie de "diagnóstico", con varias opciones posibles para el desarrollo de la "enfermedad". Un escenario muy común es cuando un jugador, después de jugar "intuición", llega al comercio automático. No me malinterpreten, no quiero poner el énfasis de tal manera que los robots comerciales rigurosos "tecnológicamente y matemáticamente" se opongan al comercio "manual" ingenuo e indefenso. Por ejemplo, yo mismo estoy convencido de que cualquiera de mis intentos de obtener ganancias de un mercado eficiente (leído de cualquier mercado transparente y líquido) a través de la especulación, ya sea discrecional o totalmente automatizada, están condenados a priori al fracaso. Si, tal vez, no permite el factor de la suerte al azar.
Sin embargo, el comercio, y en particular, el comercio algo (rítmico), es un pasatiempo popular para muchos. Algunos programan robots de negociación de forma independiente, otros van aún más lejos y crean sus propias plataformas para escribir, depurar y probar estrategias de negociación, mientras que otros descargan / compran un "experto" electrónico listo para usar. Pero incluso aquellos que no escriben algoritmos comerciales por su cuenta, deben tener una idea de cómo manejar esta "caja negra" para beneficiarse de ella de acuerdo con la idea del autor. Para no ser infundado, doy mis observaciones adicionales usando un ejemplo de una estrategia comercial simple:
Robot comercial simple
Un robot comercial analiza la dinámica del valor del oro, en dólares por onza troy, y decide "comprar" o "vender" una cierta cantidad de oro. Por simplicidad, suponemos que el robot siempre comercia en una onza troy.
Por ejemplo, al momento de la compra, el costo de una onza troy de oro era de 1075.00
USD . En el momento de la venta posterior (cierre de la transacción), el precio aumentó a 1079.00 USD. El beneficio de esta transacción ascendió a 4 USD.
Si el robot "vendió" oro a 1075.00 USD, y posteriormente completó (cerró) la transacción al "comprar" oro de nuevo a un precio de 1079 USD, el beneficio de la transacción será negativo, menos 4 USD. En realidad, no importa para nosotros cómo el robot vende oro, que no tiene, para luego "recomprarlo". Un corredor / centro de negociación le permite a un operador "comprar" y "vender" un activo de una forma u otra, ganando (o, más a menudo, perdiendo), en la diferencia en las tasas.
Decidimos los
datos de entrada para el robot; de hecho, esta es la serie temporal de precios (cotizaciones) del oro. Si dice que mi ejemplo es demasiado simple, no vital, puedo asegurarlo: la mayoría de los robots que circulan en el mercado (y de hecho los comerciantes también) en su comercio se guían solo por las estadísticas de precios de los bienes que están comercializando. En cualquier caso, en el problema de la optimización paramétrica de una estrategia comercial, no existe una diferencia fundamental entre un robot que opera sobre la base del vector de precios y un robot que accede a una matriz de terabytes de análisis de mercado de clasificación múltiple. Lo principal es que ambos robots pueden (deberían poder) probarse en datos históricos. Deben determinarse los algoritmos: es decir, en los mismos datos de entrada (tiempo del modelo, si es necesario, también podemos tomarlo como parámetro), el robot comercial debería mostrar el mismo resultado.
Se pueden encontrar más detalles sobre el robot comercial en el siguiente spoiler:
algoritmo de negociación de robot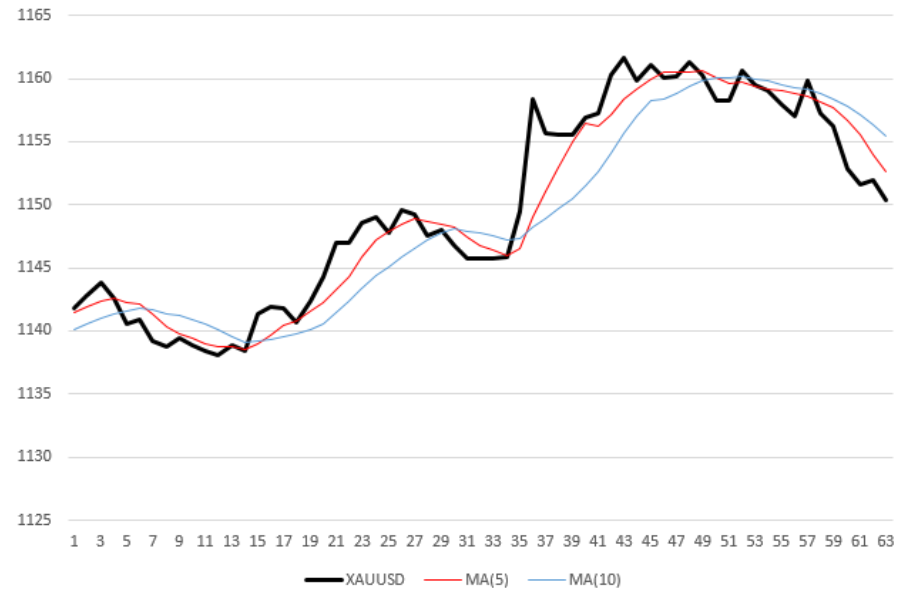
La curva negra (gruesa) en el gráfico es la medición del precio
XAUUSD por hora. Dos líneas discontinuas finas, rojo y azul: valores de precio promedio con períodos promedio de 5 y 10, respectivamente. En otras palabras, Promedio móvil (MA) con períodos de 5, 10. Por ejemplo, para calcular la ordenada del último punto (derecho) de la curva roja, tomé el promedio de los últimos 5 valores de precio. Por lo tanto, cada promedio móvil no solo se "suaviza" en relación con la curva de precios, sino que también se retrasa a la mitad de su período en relación con ella.
Regla de apertura de transacción
El robot tiene una regla simple para tomar una decisión de compra / venta:
- tan pronto como un promedio móvil con un período corto (
MA “rápido”) cruza un promedio móvil con un período largo (MA “lento”) de abajo hacia arriba, el robot compra un activo (oro).
Tan pronto como la MA "rápida" cruza la MA "lenta" de arriba a abajo, el robot vende el activo. En la figura anterior, el robot realizará 5 transacciones: 3 ventas en las marcas de tiempo 7, 31 y 50 y dos compras (marcas 16 y 36).
El robot puede abrir un número ilimitado de transacciones. Por ejemplo, en algún momento, el robot puede tener varias compras y ventas pendientes al mismo tiempo.
Regla de cierre del trato
El robot cierra el trato tan pronto como:
- el beneficio de la transacción supera el umbral especificado en porcentaje: TakeProfit,
- o la pérdida de la transacción, en porcentaje, excede el valor correspondiente: StopLoss.
Supongamos que StopLoss es 0.2%.
El acuerdo es una "venta" de oro a un precio de 1061.50.
Tan pronto como el precio del oro aumente a 1061.50 + 1061.50 * 0.2% / 100% = 1063.12%, la pérdida del trato será obviamente del 0.2% y el robot cerrará el trato automáticamente.
El robot toma todas las decisiones sobre abrir / cerrar una transacción en puntos discretos en el tiempo, al final de cada hora, después de la publicación de la próxima cotización de XAUUSD.
Sí, el robot es extremadamente simple. Al mismo tiempo, cumple al 100% los requisitos para ello:
- el algoritmo es determinista: cada vez que simulemos el trabajo del robot con los mismos datos de precios, obtendremos el mismo resultado,
- tiene un número suficiente de parámetros ajustables, a saber: el período de "rápido" y el período de promedio móvil "lento" (números naturales), TakeProfit y StopLoss - números reales positivos,
- un cambio en cada uno de los 4 parámetros, en el caso general, tiene un efecto no lineal en las características comerciales del robot, en particular, en su rentabilidad,
- la rentabilidad de un robot en el historial de precios se considera un código de programa elemental, y el cálculo en sí mismo toma una fracción de segundo para un vector de miles de cotizaciones,
- Finalmente, lo que, sin embargo, es irrelevante, el robot, con toda su simplicidad, en realidad demostrará no ser peor (aunque probablemente no mejor) que el Grial vendido por el autor en Internet por una cantidad inmoderable.
Búsqueda rápida de un conjunto cuasi óptimo de parámetros de entrada
Usando el ejemplo de nuestro robot simple, se puede ver que una enumeración completa de todos los posibles vectores de configuración del robot es demasiado costosa incluso para 4 parámetros variables. Una alternativa obvia a la búsqueda exhaustiva es la elección de vectores de parámetros para una estrategia específica. Consideramos solo una parte de todas las combinaciones posibles en busca de la mejor, en la que la
CF se aproxima a la más alta (o la más pequeña, según la CF que elijamos y el resultado que logremos).
Consideraremos tres algoritmos de búsqueda para el valor cuasi
óptimo del
filtro digital . Para cada algoritmo, establecemos un límite de 40 pruebas (de 400 combinaciones posibles).
Método Monte Carlo
o una selección aleatoria de M vectores no correlacionados entre el número posible de conjuntos igual a N. El método es probablemente el más simple posible. Lo usaremos como punto de partida para la comparación posterior con otros métodos de optimización.
Ejemplo 1
El gráfico muestra la dependencia de la ganancia (P) de nuestro robot comercial
EURUSD , obtenido en el segmento anual de la historia de las mediciones de precios por hora, en el valor del parámetro, el período del
promedio móvil "lento" (M). Todos los demás parámetros son fijos y no están optimizados.
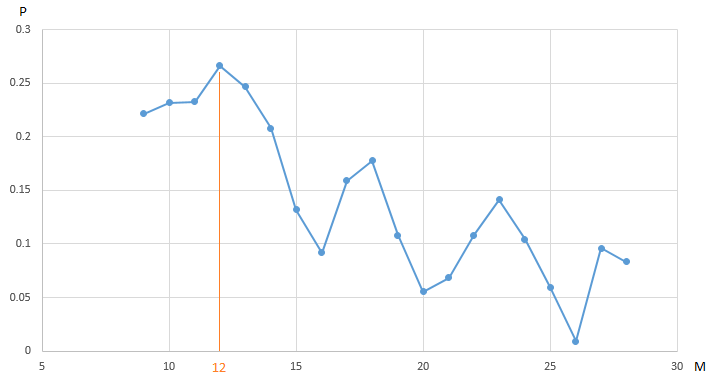
CF (ganancia) alcanza un máximo de 0.27 en el punto M = 12. Para garantizar el valor máximo de ganancia, necesitamos realizar 20 iteraciones de prueba. Una alternativa es realizar un número menor de pruebas de un robot comercial con un valor seleccionado al azar del parámetro M en el intervalo [9, 20]. Por ejemplo, después de 5 iteraciones (20% del número total de pruebas, encontramos un vector cuasi óptimo (vector, obviamente, unidimensional) de parámetros: M = 18 con un valor de CF (M) igual a 0.18:

Los valores restantes en el gráfico de nuestro algoritmo de optimización estaban ocultos por la "niebla de guerra".
La optimización de uno de los cuatro parámetros de nuestro robot comercial, con valores fijos de los parámetros restantes, no nos permite ver la imagen completa. ¿Quizás un máximo de 0.27 CF no sea el mejor valor del indicador, si varía el valor de otros parámetros?

Así es como la dependencia de la ganancia en el período promedio móvil cambia para varios valores del parámetro TakeProfit en el intervalo [0.2 ... 0.8].
Método Monte Carlo: optimización de dos parámetros.
La dependencia del beneficio de un robot comercial en dos parámetros se puede representar gráficamente como una superficie:

Los dos ejes son los valores de los parámetros T (TakeProfit) y M (período de la media móvil), el tercer eje es el valor del beneficio.
Para nuestro robot comercial, después de realizar 400 pruebas en un intervalo de datos de un año (~ 6000 cotizaciones por hora del euro frente al dólar estadounidense), obtenemos una superficie de la forma:

o, en el plano donde los valores de los activos financieros (beneficio, P) están representados por el color:

Al elegir puntos arbitrarios en el plano, en este ejemplo, el algoritmo no encontró el valor óptimo, pero se acercó bastante a él:

¿Qué tan efectivo es el método de Monte Carlo para encontrar la máxima
FQ ? Después de realizar 1,000 iteraciones de búsqueda del máximo de CF en los datos de origen del ejemplo anterior, obtuve las siguientes estadísticas:
- el valor promedio del máximo del DF encontrado durante 1,000 iteraciones de optimización (40 vectores aleatorios de parámetros [M, T] de 400 combinaciones posibles) fue 0.231 o 95.7% del máximo global del DF (0.279).
Obviamente, al comparar los métodos de optimización paramétrica de robots comerciales, una muestra no es un indicador. Pero por ahora, esta evaluación es suficiente. Pasamos al siguiente método: el método de
descenso de gradiente .
Método de descenso de gradiente
Formalmente, como su nombre lo indica, el método se utiliza para buscar el mínimo del DF.
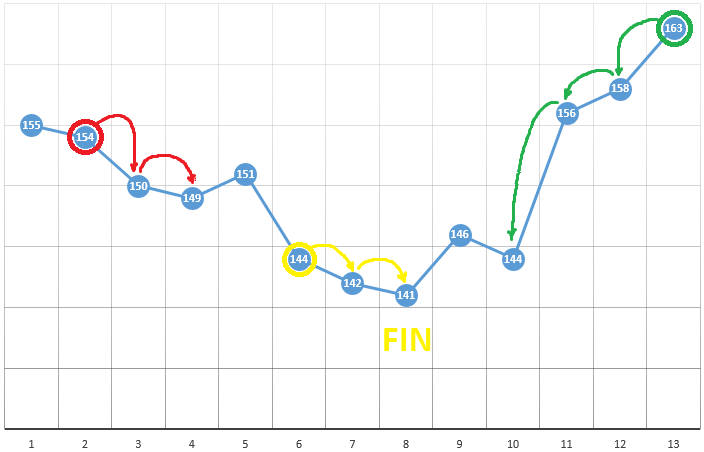
Según el método, seleccionamos el punto de partida con coordenadas [x0, y0, z0, ...]. En el ejemplo de optimización de un parámetro, este puede ser un punto seleccionado al azar:
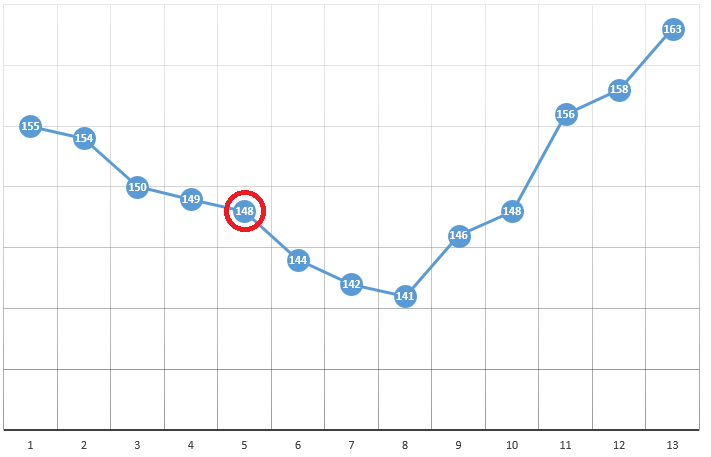
con coordenadas [5] y un valor de DF de 148. Los siguientes son tres pasos simples:
- verifique los valores de CF cerca de la posición actual (149 y 144)
- moverse al punto con el valor CF más pequeño
- si esto está ausente, se encuentra un extremo local, se completa el algoritmo

Para optimizar el DF en función de dos parámetros, utilizamos el mismo algoritmo. Si antes calculamos el CF en dos puntos vecinos
, ahora comprobamos 4 puntos:
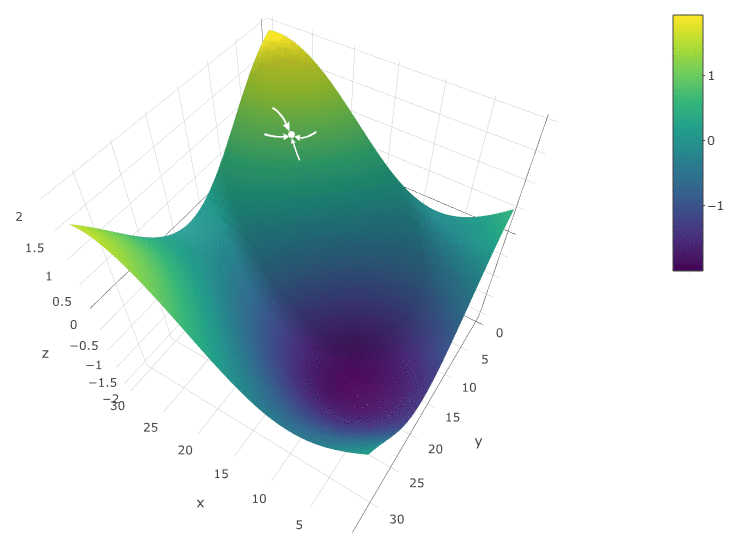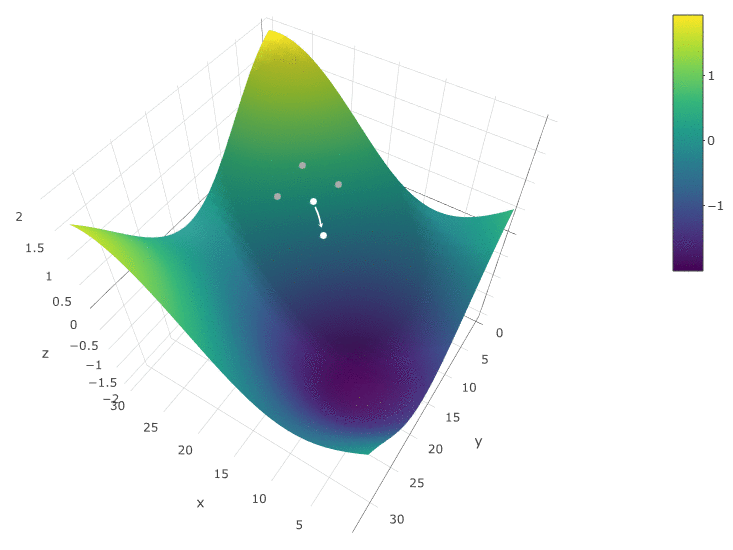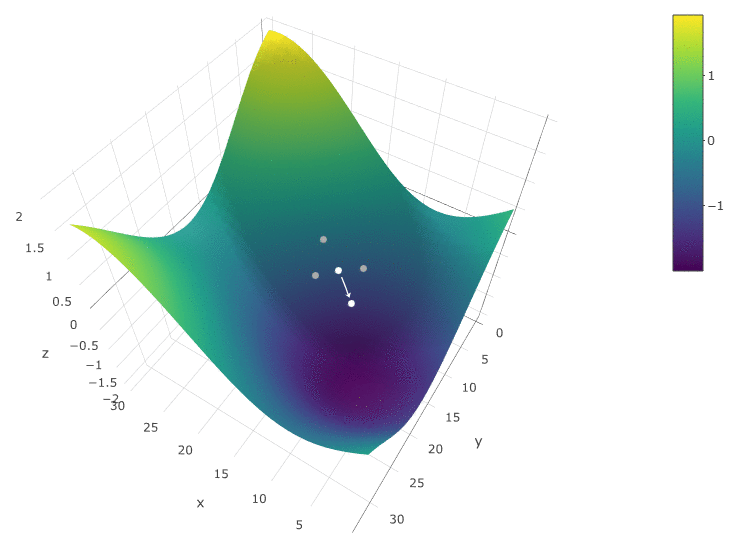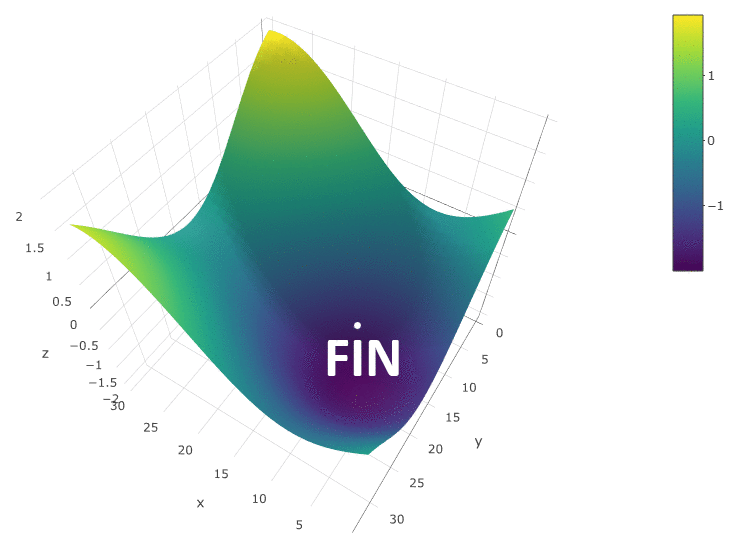
El método es definitivamente bueno cuando solo hay un extremo en un DF en un espacio de prueba. Si hay varios extremos, la búsqueda deberá repetirse varias veces para aumentar la probabilidad de encontrar un extremo global:
En nuestro ejemplo, estamos buscando el
máximo DF. Para mantener la definición del algoritmo, podemos suponer que estamos buscando un mínimo de "menos DF". De todos modos, el beneficio de un robot comercial en función del período del promedio móvil y el valor de TakeProfit, una iteración:
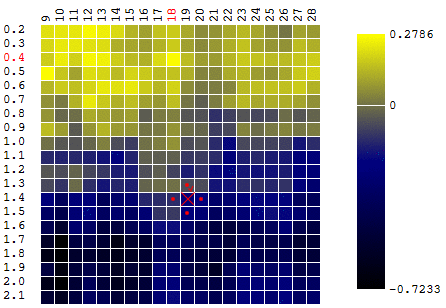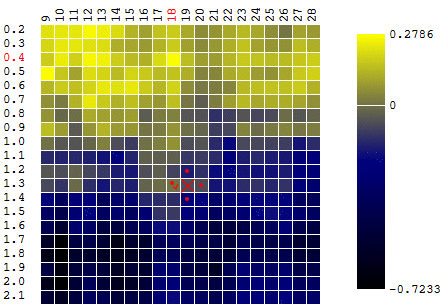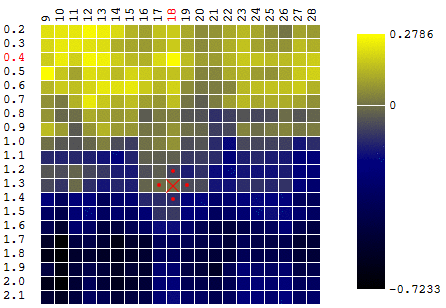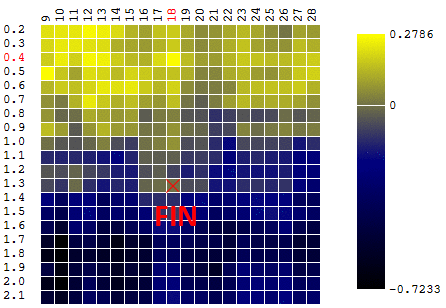
En este caso, se encontró un extremo local que está lejos del máximo global de la FQ. Un ejemplo de varias iteraciones de la búsqueda del extremo del FS por el método de descenso de gradiente, el valor del FS se calcula 40 veces (40 puntos de 400 posibles):

Ahora, comparamos la eficiencia de la búsqueda del máximo global de la CF (ganancia) en nuestros datos iniciales utilizando los algoritmos de Monte Carlo y de descenso de gradiente. En cada caso, se llevan a cabo 40 pruebas (cálculos de CF). Se realizaron 1,000 iteraciones de optimización por cada uno de los métodos:
| Montecarlo | descenso gradiente |
|---|
| el promedio del valor cuasi óptimo obtenido de la FQ | 0,231 | 0.200 |
| el valor obtenido del máximo de CF | 95,7% | 92,1% |
Como puede ver en la tabla, en este ejemplo, el método de descenso de gradiente es peor en su tarea: buscar el extremo global del activo digital: el beneficio máximo. Pero no tenemos prisa por descartarlo.
Estabilidad paramétrica del algoritmo de negociación.
Encontrar las coordenadas del máximo / mínimo global de un filtro digital a menudo no es un objetivo de optimización. Supongamos que, en el gráfico, hay un pico "agudo": un máximo global, cuyo valor de CF en las proximidades es mucho más bajo que el valor pico:
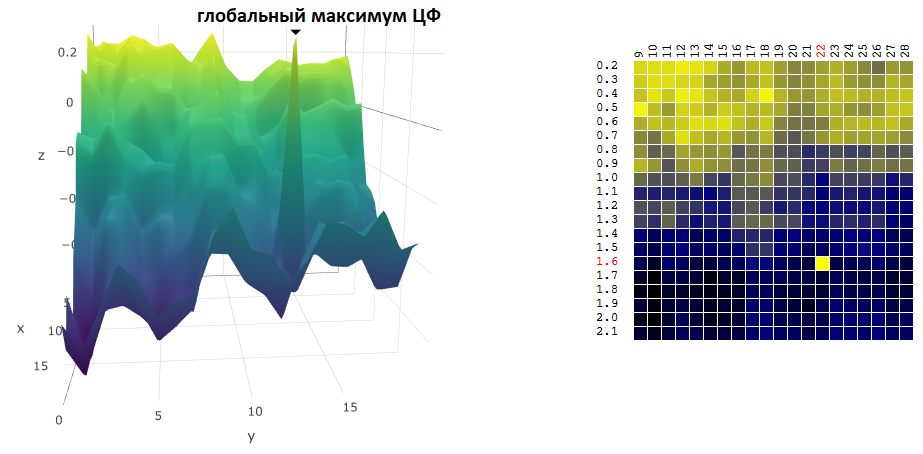
Supongamos que hemos seleccionado la configuración del robot comercial que corresponde al máximo encontrado del activo digital. Si cambiamos ligeramente el valor de al menos uno de los parámetros (el período de la media móvil y / o TakeProfit), la rentabilidad del robot caerá bruscamente (se volverá negativa). Con respecto al comercio real, al menos uno puede esperar que el mercado en el que operará nuestro robot sea notablemente diferente del período de la historia en el que optimizamos el algoritmo de comercio.
Por lo tanto, al elegir la configuración "óptima" de un robot comercial, vale la pena hacerse una idea de cuán sensible es el robot a los cambios en la configuración en las proximidades del punto extremo encontrado del DF.
Obviamente, el método de descenso de gradiente, como regla, nos da los valores de TF en la vecindad del extremo. El método de Monte Carlo es más probable que golpee cuadrados.
En múltiples instrucciones para probar estrategias de negociación automatizadas, una vez que se completa la optimización, se recomienda verificar los indicadores de destino del robot en la vecindad del vector de parámetros encontrado. Pero estas son pruebas adicionales. Además, ¿qué pasa si la rentabilidad de la estrategia cae con un ligero cambio en la configuración? Obviamente, tienes que repetir el proceso de prueba.
Un algoritmo sería útil para nosotros, que, al mismo tiempo que se busca el extremo del CF, nos permitiría evaluar la estabilidad de la estrategia comercial para cambiar la configuración en un rango estrecho con respecto a los picos encontrados. Por ejemplo, no busque directamente el máximo CF
y el valor promedio ponderado que tiene en cuenta los valores vecinos de la función objetivo, donde el peso es inversamente proporcional a la distancia al valor vecino (para optimizar dos parámetros x, y y la función objetivo P):
En otras palabras, al elegir un vector de parámetros casi óptimo, el algoritmo evaluará la función objetivo "suavizada":
fue se ha convertido
se ha convertido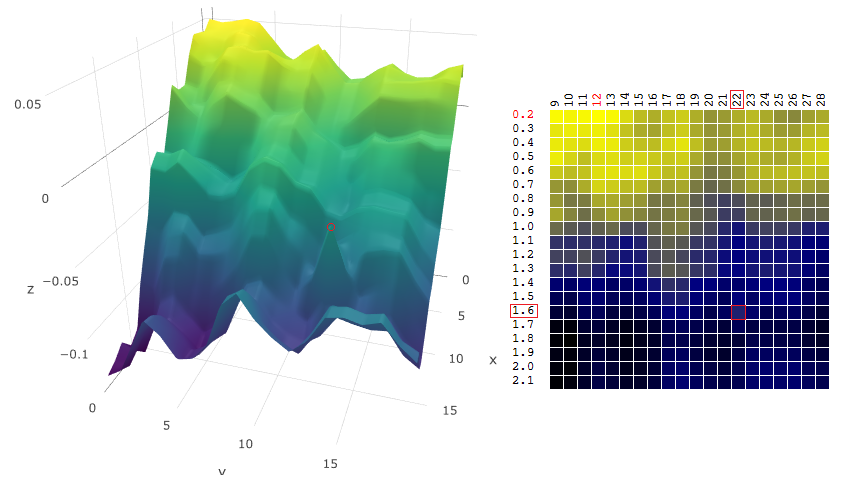
El método de "batalla naval"
Intentando combinar las ventajas de ambos métodos (Monte Carlo y el método de descenso de gradiente), probé un algoritmo similar al algoritmo del juego en la "batalla naval":
- primero, golpeo algunos "golpes" en toda el área
- entonces, en lugares de "golpes" abro fuego masivo.
En otras palabras, las primeras N pruebas se llevan a cabo en vectores aleatorios no correlacionados de parámetros de entrada. De estos, se seleccionan los M mejores resultados. En la vecindad de estas pruebas (más - minutos 0..L a cada una de las coordenadas) se llevan a cabo otras K pruebas.
Para nuestro ejemplo (400 puntos, 40 ensayos en total) tenemos:
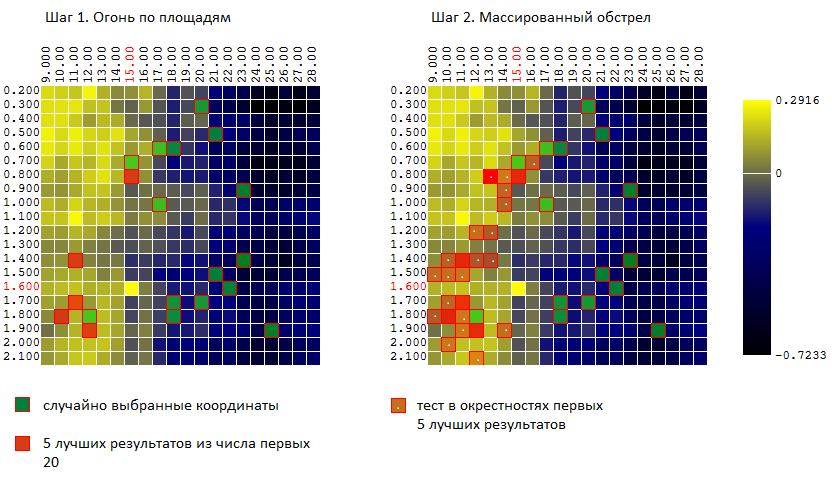
Y nuevamente, comparamos la efectividad de ahora 3 algoritmos de optimización:
| Montecarlo | descenso gradiente | "Batalla naval" |
|---|
El valor promedio del extremo encontrado de la FQ como porcentaje del valor global.
40 pruebas, 1,000 iteraciones de optimización
| 95,7% | 92,1% | 97,0% |
El resultado es alentador. Por supuesto, la comparación se realizó en una muestra de datos específica: un algoritmo de negociación en una serie de tiempo del valor del euro frente al dólar estadounidense.
Pero, antes de comparar los algoritmos en más muestras de los datos de origen, voy a hablar sobre otro, inesperadamente (¿injustificable?) Algoritmo popular para optimizar estrategias comerciales: la optimización del algoritmo genético (GA). Sin embargo, el artículo salió demasiado voluminoso, y el GA tendrá que posponerse para la próxima publicación .