Introduccion

OpenGL, que es el backend para OpenSceneGraph, utiliza primitivas geométricas (como puntos, líneas, triángulos y caras poligonales) para construir todos los objetos en el mundo tridimensional.

Estas primitivas están definidas por datos sobre sus vértices, que incluyen las coordenadas de los vértices, componentes normales, datos de color y coordenadas de textura. Estos datos se almacenan en matrices especiales. Las primitivas se pueden formar, por ejemplo, especificando para los objetos que los describen una lista de índices de vértices. Este método se llama método de matriz de vértices, elimina el almacenamiento de vértices redundantes en la memoria y tiene un buen rendimiento.

Además, OpenGL puede usar el mecanismo de las llamadas listas de visualización , cuando las primitivas preparadas en la memoria de video pueden reutilizarse, lo que acelera significativamente la visualización de objetos estáticos.

De forma predeterminada, OSG utiliza el método de matriz de vértices y el método de lista de visualización para representar la geometría. Sin embargo, la estrategia de representación puede cambiar, dependiendo de cómo se presenten los datos de geometría. En este artículo, cubriremos las técnicas básicas para trabajar con geometría en OSG.

1. Clases Geode y Drawable

La clase osg :: Geode es un terminal, el llamado nodo "hoja" del árbol de escenas. No puede tener nodos secundarios, pero contiene toda la información necesaria para representar la geometría. Su nombre, Geode, es la abreviatura de nodo de geometría.

Los datos geométricos que procesará el motor se almacenan en el conjunto de objetos de la clase osg :: Drawable, administrada por la clase osg :: Geode. La clase osg :: Drawable es una clase puramente virtual. Se heredan una serie de subclases, que son modelos tridimensionales, imágenes y texto procesados ​​por la canalización de OpenGL. OSG se refiere a dibujable como todos los elementos que puede dibujar el motor.

La clase osg :: Geode proporciona varios métodos para unir y separar elementos dibujables:

• Método público addDrawable (): pasa un puntero a un elemento dibujable en una instancia de la clase osg :: Geode. Todos estos elementos están controlados por osg :: ref_ptr <> punteros inteligentes.
  
• El método público removeDrawable () y removeDrawables () elimina el objeto de osg :: Geode y disminuye el recuento de referencias para él. El método removeDrawable () toma como parámetro único un puntero a un elemento de interés, y el método removeDrawables () toma dos parámetros: el índice inicial y el número de elementos que se eliminarán de la matriz de objetos osg :: Geode.
  
• El método getDrawable () devuelve un puntero a un elemento en el índice pasado como parámetro.
  
• El método getNumDrawables () devuelve el número total de elementos adjuntos a osg :: Geode. Por ejemplo, para eliminar todos los elementos de osg :: Geode, puede usar dicho código
  

geode->removeDrawables(0, geode->getNumDrawables()); 

2. Dibujando formas simples

OSG proporciona la clase osg :: ShapeDrawable, que es descendiente de la clase osg :: Drawable y está diseñada para crear primitivas tridimensionales simples. Esta clase incluye un objeto osg :: Shape que almacena información sobre geometría específica y otros parámetros. Las primitivas se generan utilizando el método setShape (), por ejemplo

 shapeDrawable->setShape(new osg::Box(osg::Vec3(1.0f, 0.0f, 0.0f), 10.0f, 10.0f, 5.0f)); 

crea una caja rectangular con un centro geométrico en el punto (1.0, 0.0, 0.0) con un ancho y una altura de 10 y una profundidad de 5 unidades. La clase osg :: Vec3 define un vector en el espacio tridimensional (además, también se presentan las clases osg :: Vec2 y osg :: Vec4 que describen vectores de la dimensión correspondiente).

Las primitivas más populares están representadas en OSG por las clases osg :: Box, osg :: Capsule, osg :: Cone, osg :: Cylinder y osg :: Sphere.

Considere un ejemplo de la aplicación de este mecanismo.

main.h

 #ifndef MAIN_H #define MAIN_H #include <osg/ShapeDrawable> #include <osg/Geode> #include <osgViewer/Viewer> #endif // MAIN_H 

main.cpp

 #include "main.h" int main(int argc, char *argv[]) { (void) argc; (void) argv; osg::ref_ptr<osg::ShapeDrawable> shape1 = new osg::ShapeDrawable; shape1->setShape(new osg::Box(osg::Vec3(-3.0f, 0.0f, 0.0f), 2.0f, 2.0f, 1.0f)); osg::ref_ptr<osg::ShapeDrawable> shape2 = new osg::ShapeDrawable; shape2->setShape(new osg::Cone(osg::Vec3(0.0f, 0.0f, 0.0f), 1.0f, 1.0f)); shape2->setColor(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f)); osg::ref_ptr<osg::ShapeDrawable> shape3 = new osg::ShapeDrawable; shape3->setShape(new osg::Sphere(osg::Vec3(3.0f, 0.0f, 0.0f), 1.0f)); shape3->setColor(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f)); osg::ref_ptr<osg::Geode> root = new osg::Geode; root->addDrawable(shape1.get()); root->addDrawable(shape2.get()); root->addDrawable(shape3.get()); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); } 

Este ejemplo especialmente no necesita comentarios: en el programa se crean tres formas simples, después de la compilación y el lanzamiento veremos tal resultado



El mecanismo que se muestra en el ejemplo es simple y directo, pero no es la forma más efectiva de crear geometría y puede usarse exclusivamente para pruebas. La clase osg :: Geometry se usa para crear geometría en aplicaciones basadas en OSG de alto rendimiento.

3. Almacenamiento de datos de geometría: clases osg :: Array y osg :: Geometry

La clase osg :: Array es una clase abstracta básica, de la que se heredan varios descendientes, diseñada para almacenar datos que se pasan a las funciones de OpenGL. Trabajar con esta clase es similar a trabajar con std :: vector de la biblioteca estándar de C ++. El siguiente código ilustra la adición de un vector a una matriz de vértices utilizando el método push_back ()

 vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f)); 

Las matrices OSG se asignan en el montón y se gestionan mediante punteros inteligentes. Sin embargo, esto no se aplica a los elementos de la matriz, como osg :: Vec3 u osg :: Vec2, que también se pueden crear en la pila.

La clase osg :: Geometry es un contenedor sobre las funciones de OpenGL que funcionan con matrices de vértices. Se deriva de la clase osg :: Drawable y se puede agregar fácilmente a la lista de objetos osg :: Geode. Esta clase toma las matrices descritas anteriormente como entrada y las usa para generar geometría usando OpenGL.

4. Vértices y sus atributos.

Un vértice es una unidad atómica de primitivas de geometría. Tiene una serie de atributos que describen un punto en un espacio de dos o tres dimensiones. Los atributos incluyen: posición, color, vector normal, coordenadas de textura, coordenadas de niebla, etc. La parte superior siempre debe tener una posición en el espacio, ya que para otros atributos, pueden estar presentes opcionalmente. OpenGL admite 16 atributos de vértice básicos y puede usar diferentes matrices para almacenarlos. Todas las matrices de atributos son compatibles con la clase osg :: Geometry y se pueden establecer utilizando los métodos del conjunto de formularios * Array ().

Atributos de vértices en OpenSceneGraph

Atributo	Tipo de datos	Osg :: Método de Geometría	Llamada equivalente a OpenGL
Posición	3 vectores	setVertexArray ()	glVertexPointer ()
Normal	3 vectores	setNormalArray ()	glNormalPointer ()
Color	4-vector	setColorArray ()	glColorPointer ()
Color secundario	4-vector	setSecondaryColorArray ()	glSecondaryColorPointerEXT ()
Coordenadas de niebla	flotar	setFogCoordArray ()	glFogCoordPointerEXT ()
Coordenadas de textura	2 o 3 vectores	setTexCoordArray ()	glTexCoordPointer ()
Otros atributos	Definido por el usuario	setVertexArribArray ()	glVertexAttribPointerARB ()

En principio, es necesario establecer sus propios atributos para cada uno de los vértices, lo que conduce a la formación de varias matrices de atributos del mismo tamaño; de lo contrario, una falta de coincidencia en los tamaños de las matrices puede conducir a un comportamiento indefinido del motor. OSG admite varios métodos para vincular atributos de vértices, por ejemplo

 geom->setColorBinding(osg::Geometry::BIND_PER_VERTEX); 

significa que cada vértice y cada color del vértice están correlacionados uno a uno entre sí. Sin embargo, si nos fijamos en dicho código

 geom->setColorBinding(osg::Geometry::BIND_OVERALL); 

luego aplica un color a toda la geometría. Del mismo modo, las relaciones entre otros atributos se pueden configurar llamando a los métodos setNormalBinding (), setSecondaryColorBinding (), setFogCoordBinding () y setVertexAttribBinding ().

5. Conjuntos de primitivas de geometría

El siguiente paso después de definir las matrices de atributos de vértice es describir cómo se representarán los datos de vértice. La clase virtual osg :: PrimitiveSet se usa para controlar las primitivas geométricas generadas por el renderizador a partir de un conjunto de vértices. La clase osg :: Geometry proporciona varios métodos para trabajar con conjuntos de primitivas de geometría:

• addPrimitiveSet (): pasa un puntero a un conjunto de primitivas en un objeto osg :: Geometry.
  
• removePrimitiveSet (): elimina un conjunto de primitivas. Como parámetros, toma el índice inicial de conjuntos y el número de conjuntos que se eliminarán.
  
• getPrimitiveSet (): devuelve un conjunto de primitivas en el índice pasado como parámetro.
  
• getNumPrimitiveSets (): devuelve el número total de conjuntos de primitivas asociadas con esta geometría.
  

La clase osg :: PrimitiveSet es abstracta y no se puede instanciar, pero varias clases derivadas que encapsulan conjuntos de primitivas con las que opera OpenGL, como osg :: DrawArrays y osg :: DrawElementsUInt, heredan de ella.

La clase osg :: DrawArrays usa varios elementos consecutivos de una matriz de vértices para construir una primitiva geométrica. Se puede crear y adjuntar a la geometría llamando a un método.

 geom->addPrimitiveSet(new osg::DrawArrays(mode, first, count)); 

El primer modo de parámetro establece el tipo primitivo en los tipos primitivos OpenGL correspondientes: GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_QUAD_STRIP, GL_QUADS y GL_POLY.

El primer y segundo parámetro especifican el primer índice en la matriz de vértices y el número de vértices a partir del cual se debe generar la geometría. Además, OSG no comprueba si el número especificado de vértices es suficiente para construir la geometría especificada por el modo, ¡lo que puede provocar el bloqueo de la aplicación!

6. Ejemplo: dibuja un cuadrado pintado

Implementamos todo lo anterior como un ejemplo simple


Después de la compilación y ejecución, obtenemos un resultado similar a este



Este ejemplo necesita aclaración. Entonces, en primer lugar, creamos una matriz de vértices del cuadrado, en el que se almacenan sus coordenadas

 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array; vertices->push_back(osg::Vec3(0.0f, 0.0f, 0.0f)); vertices->push_back(osg::Vec3(1.0f, 0.0f, 0.0f)); vertices->push_back(osg::Vec3(1.0f, 0.0f, 1.0f)); vertices->push_back(osg::Vec3(0.0f, 0.0f, 1.0f)); 

A continuación establecemos la matriz de normales. En nuestro caso simple, no necesitamos crear una normal para cada vértice, solo describa un vector unitario dirigido perpendicularmente al plano del cuadrado

 osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array; normals->push_back(osg::Vec3(0.0f, -1.0f, 0.0f)); 

Establecer un color para cada vértice

 osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array; colors->push_back(osg::Vec4(1.0f, 0.0f, 0.0f, 1.0f)); colors->push_back(osg::Vec4(0.0f, 1.0f, 0.0f, 1.0f)); colors->push_back(osg::Vec4(0.0f, 0.0f, 1.0f, 1.0f)); colors->push_back(osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f)); 

Ahora cree un objeto de geometría donde se almacenará la descripción de nuestro cuadrado, que será procesada por el render. Pasamos una matriz de vértices a esta geometría.

 osg::ref_ptr<osg::Geometry> quad = new osg::Geometry; quad->setVertexArray(vertices.get()); 

Al pasar una serie de normales, informamos al motor que se usará una sola normal para todos los vértices, especificando el método de enlace ("enlace") de los normales BIND_OVAERALL

 quad->setNormalArray(normals.get()); quad->setNormalBinding(osg::Geometry::BIND_OVERALL); 

Al pasar los colores de los vértices, por el contrario, indicamos que cada vértice tendrá su propio color.

 quad->setColorArray(colors.get()); quad->setColorBinding(osg::Geometry::BIND_PER_VERTEX); 

Ahora cree un conjunto de primitivas para la geometría. Indicamos que las caras cuadradas (GL_QUADS) deben generarse a partir de la matriz de vértices, tomando el vértice con índice 0 como primer vértice, y el número total de vértices será 4

 quad->addPrimitiveSet(new osg::DrawArrays(GL_QUADS, 0, 4)); 

Bueno, creo que no vale la pena explicar la transferencia de geometría y el lanzamiento del render

 osg::ref_ptr<osg::Geode> root = new osg::Geode; root->addDrawable(quad.get()); osgViewer::Viewer viewer; viewer.setSceneData(root.get()); return viewer.run(); 

El código anterior es equivalente al siguiente diseño en OpenGL puro

 static const GLfloat vertices[][3] = { … }; glEnableClientState( GL_VERTEX_ARRAY ); glVertexPointer( 4, GL_FLOAT, 0, vertices ); glDrawArrays( GL_QUADS, 0, 4 ); 

7. Indización de vértices en primitivas

La clase osg :: DrawArrays funciona bien cuando se leen datos de vértices directamente desde matrices, sin espacios. Sin embargo, esto no es tan efectivo cuando el mismo vértice puede pertenecer a varias caras de un objeto. Veamos un ejemplo.



El cubo tiene ocho vértices. Sin embargo, como se puede ver en la figura (observamos el despliegue del cubo en el plano), algunos vértices pertenecen a más de una cara. Si construyes un cubo de 12 caras triangulares, estos vértices se repetirán, y en lugar de una matriz de 8 vértices, obtendremos una matriz de 36 vértices, ¡la mayoría de los cuales son en realidad el mismo vértice!

Las clases OSG osg :: DrawElementsUInt, osg :: DrawElementsUByte y osg :: DrawElementsUShort, que utilizan matrices de índice de vértices como datos, están diseñadas para resolver el problema descrito. Las matrices de índices almacenan índices de vértices de primitivas que describen caras y otros elementos de geometría. Al aplicar estas clases para un cubo, es suficiente almacenar una matriz de ocho vértices que están asociados con caras a través de matrices de índices.

Las clases de tipo osg :: DrawElements * se construyen de la misma manera que la clase estándar std :: vector. Dicho código se puede usar para agregar índices.

 osg::ref_ptr<osg::DrawElementsUInt> de = new osg::DrawElementsUInt(GL_TRIANGLES); de->push_back(0); de->push_back(1); de->push_back(2); de->push_back(3); de->push_back(0); de->push_back(2); 

Este código define la cara frontal del cubo que se muestra en la figura.

Consideremos un ejemplo ilustrativo más: un octaedro



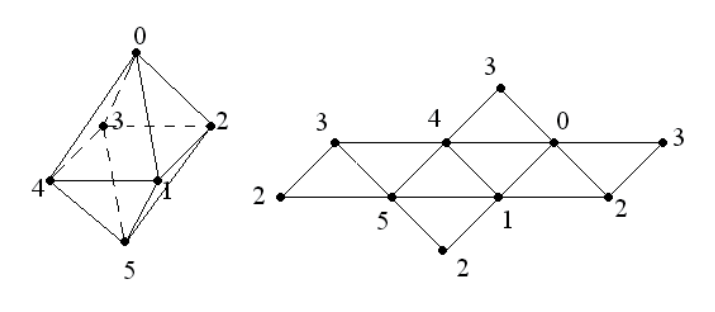
Es interesante porque contiene solo seis vértices, ¡pero cada vértice ingresa hasta cuatro caras triangulares! Podemos crear una matriz de 24 vértices para mostrar las ocho caras usando osg :: DrawArrays. Sin embargo, haremos lo contrario: almacenaremos los vértices en una matriz de seis elementos y generaremos caras usando la clase osg :: DrawElementsUInt.


Analicemos este código con más detalle. Por supuesto, lo primero que hacemos es crear una matriz de seis vértices

 osg::ref_ptr<osg::Vec3Array> vertices = new osg::Vec3Array(6); (*vertices)[0].set( 0.0f, 0.0f, 1.0f); (*vertices)[1].set(-0.5f, -0.5f, 0.0f); (*vertices)[2].set( 0.5f, -0.5f, 0.0f); (*vertices)[3].set( 0.5f, 0.5f, 0.0f); (*vertices)[4].set(-0.5f, 0.5f, 0.0f); (*vertices)[5].set( 0.0f, 0.0f, -1.0f); 

Inicializamos cada vértice directamente accediendo al vector de sus coordenadas usando la operación de desreferenciación del puntero y el operador [] (recordamos que osg :: Array es similar en su dispositivo a std :: vector).

Ahora cree caras como una lista de índices de vértices

 osg::ref_ptr<osg::DrawElementsUInt> indices = new osg::DrawElementsUInt(GL_TRIANGLES, 24); (*indices)[ 0] = 0; (*indices)[ 1] = 1; (*indices)[ 2] = 2; //  0 (*indices)[ 3] = 0; (*indices)[ 4] = 4; (*indices)[ 5] = 1; //  1 (*indices)[ 6] = 4; (*indices)[ 7] = 5; (*indices)[ 8] = 1; //  2 (*indices)[ 9] = 4; (*indices)[10] = 3; (*indices)[11] = 5; //  3 (*indices)[12] = 3; (*indices)[13] = 2; (*indices)[14] = 5; //  4 (*indices)[15] = 1; (*indices)[16] = 5; (*indices)[17] = 2; //  5 (*indices)[18] = 3; (*indices)[19] = 0; (*indices)[20] = 2; //  6 (*indices)[21] = 0; (*indices)[22] = 3; (*indices)[23] = 4; //  7 

Las caras serán triangulares, habrá 8, lo que significa que la lista de índices debe contener 24 elementos. Los índices de caras van secuencialmente en esta matriz: por ejemplo, la cara 0 está formada por los vértices 0, 1 y 2; cara 1 - vértices 0, 4 y 1; cara 2 - vértices 4, 5 y 1 y así sucesivamente. Los vértices se enumeran en el sentido contrario a las agujas del reloj si observa la cara de la cara (consulte la figura anterior).

Pasos adicionales para crear la geometría que realizamos en los ejemplos anteriores. Lo único que no hicimos fue la generación automática de normales suavizados (promediados), que realizamos en este ejemplo llamando

 osgUtil::SmoothingVisitor::smooth(*geom); 

De hecho, si se dan los vértices de una cara, entonces es fácil calcular lo normal. En los vértices en los que convergen varias caras, se calcula un cierto promedio normal: se suman las normales de las caras convergentes y la suma resultante se normaliza nuevamente. Estas operaciones (¡y muchas más!) Pueden ser realizadas por el propio motor utilizando clases de la biblioteca osgUtil. Por lo tanto, en nuestro ejemplo, agregaremos una instrucción al enlazador para construir nuestro programa con esta biblioteca en el archivo * .pro

octahedron.pro

 CONFIG(debug, debug|release) { TARGET = $$join(TARGET,,,_d) . . . LIBS += -L$$OSG_LIB_DIRECTORY -losgUtild } else { . . . LIBS += -L$$OSG_LIB_DIRECTORY -losgUtil } 

Como resultado, obtenemos el siguiente resultado



Para entender cómo funciona esto, considere la canalización de OpenGL



El mecanismo de matriz de vértices reduce la cantidad de llamadas OpenGL. Almacena datos de vértices en la memoria de la aplicación, que se usa en el lado del cliente. La canalización de OpenGL en el lado del servidor obtiene acceso a varias matrices de vértices. Como se muestra en el diagrama, OpenGL recibe datos del búfer de vértices en el lado del cliente y, de manera ordenada, realiza el ensamblaje de primitivas. Así es como se procesan los datos utilizando los métodos set * Array () de la clase osg :: Geometry. La clase osg :: DrawArrays revisa estas matrices directamente y las muestra.

Cuando se usa osg :: DrawElements *, se reduce la dimensión de las matrices de vértices y se reduce el número de vértices transferidos a la tubería. Una matriz de índices le permite crear un caché de vértices en el lado del servidor. OpenGL lee datos de vértices de la memoria caché, en lugar de leer desde el búfer de vértices en el lado del cliente. Esto aumenta significativamente el rendimiento general de renderizado.

8. Técnicas de procesamiento de mallas poligonales.

OpenSceneGraph admite varias técnicas para procesar la malla poligonal de los objetos de geometría de escena. Estos métodos de preprocesamiento, como la reducción de polígonos y la teselación, a menudo se utilizan para crear y optimizar modelos poligonales. Tienen una interfaz simple, pero en el proceso realizan muchos cálculos complejos y no son muy adecuados para la ejecución sobre la marcha.

Las técnicas descritas incluyen:

1. osgUtil :: Simplifier - reduciendo el número de triángulos en geometría. El método público simplify () se usa para simplificar la geometría del modelo.
   
2. osgUtil :: SmootingVisitor - cálculo de normales. El método smooth () se puede usar para generar normales suavizadas para el modelo, en lugar de calcularlas independientemente y establecerlas explícitamente a través de una matriz de normales.
   
3. osgUtil :: TangentSpaceGenerator - generación de vectores de base tangente para vértices modelo. Se inicia llamando al método generate () y guarda el resultado devuelto por los métodos getTangentArray (), getNormalArray () y getBinormalArray (). Estos resultados se pueden usar para varios atributos de vértice al escribir sombreadores en GLSL.
   
4. osgUtil :: Tesselator - realiza la teselación de una malla poligonal - divide primitivas complejas en una secuencia de simples (método retesselatePolygons ())
   
5. osgUtil :: TriStripVisitor - convierte una superficie geométrica en un conjunto de tiras de caras triangulares, lo que permite renderizar con un consumo eficiente de memoria. El método stripify () convierte un conjunto de primitivas del modelo en geometría basada en el conjunto GL_TRIANGLE_STRIP.
   

Todos los métodos aceptan la geometría del objeto como un parámetro pasado por osg :: Geometry & link, por ejemplo así

 osgUtil::TriStripVisitor tsv; tsv.stripify(*geom); 

donde geom se refiere a una instancia de geometría descrita por un puntero inteligente.

Las clases osg :: Simplifier, osg :: SmoothingVisitor y osg :: TriStripVisitor pueden trabajar directamente con nodos en el gráfico de escena, por ejemplo

 osgUtil::TriStripVisitor tsv; node->accept(tsv); 

El método accept () procesa todos los nodos secundarios hasta que la operación especificada se aplica a todos los nodos terminales de esta parte del árbol de escenas almacenadas en nodos del tipo osg :: Geode.

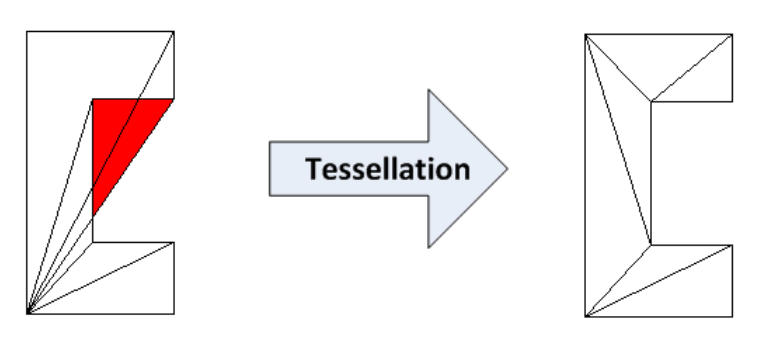
Probemos la técnica de teselación en la práctica.


En base a la posición espacial de los vértices en este ejemplo, vemos que estamos tratando de crear un polígono no convexo de ocho vértices, utilizando la generación de una cara del tipo GL_POLYGON. El ensamblaje y la ejecución de este ejemplo muestra que el resultado que esperamos no funciona: el ejemplo se muestra incorrectamente



Para solucionar este problema, la geometría construida debe estar teselada antes de pasarla al espectador.

 osgUtil::Tessellator ts; ts.retessellatePolygons(*geom); 

después de lo cual obtenemos el resultado correcto



Como funciona Un polígono no convexo, sin el uso de la teselación correcta, no se mostrará como esperamos, ya que OpenGL, que busca optimizar el rendimiento, lo considerará como un polígono convexo simple o simplemente lo ignorará, lo que puede dar resultados completamente inesperados.

La clase osgUtil :: Tessellator utiliza algoritmos para transformar un polígono convexo en una serie de no convexos; en nuestro caso, transforma la geometría en GL_TRIANGLE_STRIP.



Esta clase puede manejar polígonos de agujeros y polígonos de auto-intersección. Usando el método public setWindingType (), puede definir varias reglas de procesamiento, como GLU_TESS_WINDING_ODD o GLU_TESS_WINDING_NONZERO, que especifican las regiones internas y externas de un polígono complejo.

Conclusión

En este artículo, obtuvimos una comprensión básica de cómo la geometría de los objetos tridimensionales se almacena y procesa en el motor OSG. No piense que esos ejemplos simples y no demasiado impresionantes que se consideran en el artículo son el límite de las capacidades del motor. Solo estos ejemplos pueden ayudar al desarrollador a comprender la mecánica de OpenSceneGraph, y sin esta comprensión es difícil imaginar el trabajo de cosas más complejas.

Este artículo se basa en la traducción y el procesamiento del texto de los capítulos correspondientes del libro OpenSceneGraph 3.0. Guía para principiantes . Todos los ejemplos los compruebo personalmente y su código fuente está disponible aquí . Continuará ...