Introduccion

Cuando se dibuja un punto, línea o polígono complejo en un mundo tridimensional, el resultado final finalmente se mostrará en una pantalla plana y bidimensional. En consecuencia, los objetos tridimensionales pasan por una cierta ruta de transformación, convirtiéndose en un conjunto de píxeles que se muestran en una ventana bidimensional.

El desarrollo de herramientas de software que implementan gráficos tridimensionales ha llegado, independientemente de cuál elija, a aproximadamente el mismo concepto de descripciones matemáticas y algorítmicas de las transformaciones anteriores. Ideológicamente, las API gráficas "limpias" como OpenGL, y los motores de juegos geniales como Unity y Unreal, utilizan mecanismos similares para describir la transformación de una escena tridimensional. OpenSceneGraph no es una excepción.

En este artículo, revisaremos los mecanismos para agrupar y transformar objetos tridimensionales en OSG.

1. Matriz modelo, matriz de vista y matriz de proyección

Tres matrices básicas involucradas en la transformación de coordenadas están involucradas en la transformación entre diferentes sistemas de coordenadas. A menudo, en términos de OpenGL, se denominan matriz modelo , matriz de vista y matriz de proyección .

La matriz del modelo se usa para describir la ubicación del objeto en el mundo 3D. Convierte los vértices del sistema de coordenadas local del objeto al sistema de coordenadas mundial . Por cierto, todos los sistemas de coordenadas en OSG son diestros .

El siguiente paso es la transformación de las coordenadas mundiales en un espacio de vista, realizado utilizando la matriz de vista. Supongamos que tenemos una cámara ubicada en el origen del sistema de coordenadas mundial. La matriz inversa a la matriz de transformación de la cámara se usa realmente como una matriz de vista. En un sistema de coordenadas diestro, OpenGL, por defecto, siempre define una cámara ubicada en el punto (0, 0, 0) del sistema de coordenadas global y dirigida a lo largo de la dirección negativa del eje Z.

Observo que en OpenGL la matriz del modelo y la matriz de vista no están separadas. Sin embargo, la matriz de vista de modelo se determina allí, lo que convierte las coordenadas locales del objeto en las coordenadas del espacio de vista. Esta matriz, de hecho, es el producto de la matriz modelo y la matriz de la forma. Por lo tanto, la transformación de un vértice V de coordenadas locales a un espacio de la forma se puede escribir condicionalmente como el producto

Ve = V * modelViewMatrix 

La siguiente tarea importante es determinar cómo se proyectarán los objetos 3D en el plano de la pantalla y calcular la llamada pirámide de recorte , un área de espacio que contiene objetos que se mostrarán en la pantalla. La matriz de proyección se utiliza para especificar la pirámide de recorte definida en el espacio mundial por seis planos: izquierdo, derecho, inferior, superior, cercano y lejano. OpenGL proporciona la función gluPerapective (), que le permite especificar una pirámide de recorte y una forma de proyectar un mundo tridimensional en un plano.

El sistema de coordenadas obtenido después de las transformaciones anteriores se denomina sistema de coordenadas normalizado del dispositivo , tiene un rango de coordenadas de -1 a 1 en cada eje y es zurdo. Y, como último paso, los datos recibidos se proyectan en el puerto de visualización (ventana gráfica) de la ventana, definido por el rectángulo del área del cliente de la ventana. Después de eso, el mundo 3D aparece en nuestra pantalla 2D. El valor final de las coordenadas de pantalla de los vértices Vs puede expresarse mediante la siguiente transformación

 Vs = V * modelViewMatrix * projectionMatrix * windowMatrix 

o

 Vs = V * MVPW 

donde MVPW es la matriz de transformación equivalente igual al producto de tres matrices: matrices de vista de modelo, matrices de proyección y matrices de ventana.

Vs en esta situación es un vector tridimensional que determina la posición de un píxel 2D con un valor de profundidad. Al invertir la operación de transformación de coordenadas, obtenemos una línea en el espacio tridimensional. Por lo tanto, un punto 2D puede considerarse como dos puntos: uno en el cercano (Zs = 0), el otro en el plano de recorte lejano (Zs = 1). Las coordenadas de estos puntos en el espacio tridimensional.

 V0 = (Xs, Ys, 0) * invMVPW V1 = (Xs, Ys, 1) * invMVPW 

donde invMVPW es el inverso de MVPW.

En todos los ejemplos discutidos hasta ahora, creamos un único objeto tridimensional en las escenas. En estos ejemplos, las coordenadas locales del objeto siempre coincidieron con las coordenadas globales globales. Ahora es el momento de hablar sobre las herramientas que le permiten colocar muchos objetos en la escena y cambiar su posición en el espacio.

2. Agrupar nodos

La clase osg :: Group es el llamado nodo de grupo de un gráfico de escena en OSG. Puede tener cualquier número de nodos secundarios, incluidos los nodos hoja de geometría u otros nodos de grupo. Estos son los nodos más utilizados con amplia funcionalidad.

La clase osg :: Group se deriva de la clase osg :: Node y, en consecuencia, hereda de la clase osg :: Referenced. osg :: Group contiene una lista de nodos secundarios, donde cada nodo secundario está controlado por un puntero inteligente. Esto asegura que no haya pérdidas de memoria cuando se conecta en cascada una rama de un árbol de escena. Esta clase proporciona al desarrollador una serie de métodos públicos.

1. addChild (): agrega el nodo al final de la lista de nodos secundarios. Por otro lado, existe el método insertChild (), que coloca el nodo secundario en una posición específica en la lista, que se especifica mediante un índice entero o un puntero al nodo, pasado como un parámetro.
   
2. removeChild () y removeChildren (): elimina un solo nodo o grupo de nodos.
   
3. getChild (): obtener un puntero a un nodo por su índice en la lista
   
4. getNumChildren (): obtiene el número de nodos secundarios asociados a este grupo.
   

Administración del nodo principal

Como ya sabemos, la clase osg :: Group gestiona grupos de sus objetos secundarios, entre los cuales puede haber instancias osg :: Geode que controlan la geometría de los objetos de escena. Ambas clases tienen una interfaz para administrar nodos primarios.

OSG permite que los nodos de escena tengan múltiples nodos principales (hablaremos de esto algún día más tarde). Mientras tanto, veremos los métodos definidos en osg :: Node que se utilizan para manipular los nodos principales:

1. getParent (): devuelve un puntero de tipo osg :: Group que contiene una lista de nodos principales.
   
2. getNumParants (): devuelve el número de nodos principales.
   
3. getParentalNodePath (): devuelve todas las rutas posibles al nodo raíz de la escena desde el nodo actual. Devuelve una lista de variables de tipo osg :: NodePath.
   

osg :: NodePath es un std :: vector de punteros a nodos de escena.



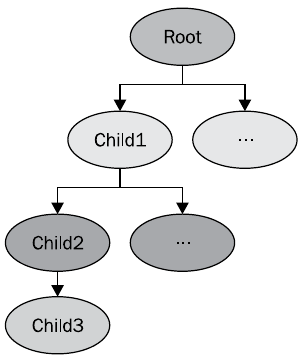
Por ejemplo, para la escena que se muestra en la figura, el siguiente código

 osg::NodePath &nodePath = child3->getParentalNodePaths()[0]; for (unsigned int i = 0; i < nodePath.size(); ++i) { osg::Node *node = nodePath[i]; // -    } 

devolverá nodos Root, Child1, Child2.

No debe utilizar mecanismos de administración de memoria para hacer referencia a los nodos principales. Cuando se elimina un nodo principal, todos los nodos secundarios se eliminan automáticamente, lo que puede provocar un bloqueo de la aplicación.

3. Agregar múltiples modelos al árbol de escenas

Ilustramos el mecanismo para usar grupos con el siguiente ejemplo.


Fundamentalmente, el ejemplo difiere de todos los anteriores en que cargamos dos modelos tridimensionales, y para agregarlos a la escena, creamos un nodo raíz grupal y le agregamos nuestros modelos como nodos secundarios

 osg::ref_ptr<osg::Group> root = new osg::Group; root->addChild(model1.get()); root->addChild(model2.get()); 

Como resultado, obtenemos una escena que consta de dos modelos: un avión y una divertida vaca espejo. Por cierto, una vaca espejo no será espejo a menos que copie su textura de OpenSceneGraph-Data / Images / reflect.rgb en el directorio data / Images de nuestro proyecto.

La clase osg :: Group puede aceptar cualquier tipo de nodos como hijos, incluidos los nodos de su tipo. Por el contrario, la clase osg :: Geode no contiene ningún nodo secundario en absoluto; es un nodo terminal que contiene la geometría del objeto de escena. Este hecho es conveniente cuando se pregunta si el nodo es un nodo de tipo osg :: Group u otro tipo de derivado de osg :: Node. Veamos un pequeño ejemplo.

 osg::ref_ptr<osg::Group> model = dynamic_cast<osg::Group *>(osgDB::readNodeFile("../data/cessna.osg")); 

El valor devuelto por la función osgDB :: readNodeFile () siempre es del tipo osg :: Node *, pero se puede convertir a su descendiente osg :: Group *. Si el nodo del modelo Cessna es un nodo de grupo, la conversión tendrá éxito; de lo contrario, la conversión devolverá NULL.

También puedes realizar el mismo truco que funciona en la mayoría de los compiladores

 //      osg::ref_ptr<osg::Group> group = ...; //     osg::Node* node1 = dynamic_cast<osg::Node*>( group.get() ); //      osg::Node* node2 = group.get(); 

En lugares de código de rendimiento crítico, es mejor usar métodos de conversión especiales

 osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("cessna.osg"); osg::Group* convModel1 = model->asGroup(); //   osg::Geode* convModel2 = model->asGeode(); //  NULL. 

4. Nodos de transformación.

Los nodos Osg :: Group no pueden realizar ninguna transformación, excepto la capacidad de ir a sus nodos secundarios. OSG proporciona la clase osg :: Transform para el movimiento de geometría espacial. Esta clase es una sucesora de la clase osg :: Group, pero también es abstracta: en la práctica, se utilizan sus herederos, que implementan diversas transformaciones espaciales de la geometría. Al recorrer el gráfico de escena, el nodo osg :: Transform agrega su transformación a la matriz de transformación actual de OpenGL. Esto es equivalente a multiplicar las matrices de transformación de OpenGL por el comando glMultMatrix ()



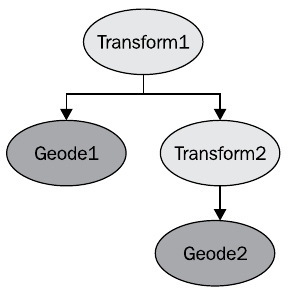
Este ejemplo de gráfico de escena se puede traducir al siguiente código de OpenGL

 glPushMatrix(); glMultMatrix( matrixOfTransform1 ); renderGeode1(); glPushMatrix(); glMultMatrix( matrixOfTransform2 ); renderGeode2(); glPopMatrix(); glPopMatrix(); 

Podemos decir que la posición de Geode1 se establece en el sistema de coordenadas Transform1, y la posición de Geode2 se establece en el sistema de coordenadas Transform2, desplazamiento relativo a Transform1. Al mismo tiempo, el posicionamiento en coordenadas absolutas se puede habilitar en OSG, lo que conducirá al comportamiento del objeto, equivalente al resultado del comando glGlobalMatrix () OpenGL

 transformNode->setReferenceFrame( osg::Transform::ABSOLUTE_RF ); 

Puede volver al modo de posicionamiento relativo

 transformNode->setReferenceFrame( osg::Transform::RELATIVE_RF ); 

5. El concepto de una matriz de transformación de coordenadas.

El tipo osg :: Matrix es un tipo OSG básico no controlado por punteros inteligentes. Proporciona una interfaz para operaciones en matrices 4x4 que describen la transformación de coordenadas, como mover, rotar, escalar y calcular proyecciones. La matriz se puede especificar explícitamente.

 //   44 osg::Matrix mat(1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f, 0.0f, 0.0f, 0.0f, 0.0f, 1.0f ); 

La clase osg :: Matrix proporciona los siguientes métodos públicos:

1. postMult () y operator * (): la multiplicación correcta de la matriz actual por la matriz o el vector pasado como parámetro. El método preMult () realiza la multiplicación izquierda.
   
2. makeTranslate (), makeRotate () y makeScale (): restablece la matriz actual y crea una matriz 4x4 que describe el movimiento, la rotación y la escala. sus versiones estáticas translate (), rotate () y scale () se pueden usar para crear un objeto matricial con parámetros específicos.
   
3. invert (): calcula el inverso de la matriz actual. Su versión estática de inverse () toma una matriz como parámetro y devuelve una nueva matriz inversa a la dada.
   

OSG entiende las matrices como matrices de cadenas y los vectores como cadenas, por lo tanto, para aplicar una transformación matricial a un vector, haga esto

 osg::Matrix mat = …; osg::Vec3 vec = …; osg::Vec3 resultVec = vec * mat; 

El orden de las operaciones matriciales es fácil de entender al observar cómo se multiplican las matrices para obtener una conversión equivalente

 osg::Matrix mat1 = osg::Matrix::scale(sx, sy, sz); osg::Matrix mat2 = osg::Matrix::translate(x, y, z); osg::Matrix resultMat = mat1 * mat2; 

El desarrollador debe leer el proceso de transformación de izquierda a derecha. Es decir, en el fragmento de código descrito, el vector primero se escala y luego su movimiento.

osg :: Matrixf contiene elementos de tipo float.

6. Usando la clase osg :: MatrixTransform

Aplicamos el conocimiento teórico adquirido en la práctica al cargar dos modelos de aviones en diferentes puntos de la escena.


El ejemplo es realmente bastante trivial. Cargando el modelo de avión desde el archivo

 osg::ref_ptr<osg::Node> model = osgDB::readNodeFile("../data/cessna.osg"); 

Crear un nodo de transformación

 osg::ref_ptr<osg::MatrixTransform> transform1 = new osg::MatrixTransform; 

Configuramos el modelo para mover el modelo a lo largo del eje X 25 unidades hacia la izquierda como matriz de transformación

 transform1->setMatrix(osg::Matrix::translate(-25.0, 0.0, 0.0)); 

Establecemos nuestro modelo para el nodo de transformación como un nodo hijo

 transform1->addChild(model.get()); 

Hacemos lo mismo con la segunda transformación, pero como matriz establecemos el movimiento a la derecha en 25 unidades.

 osg::ref_ptr<osg::MatrixTransform> transform2 = new osg::MatrixTransform; transform2->setMatrix(osg::Matrix::translate(25.0, 0.0, 0.0)); transform2->addChild(model.get()); 

Creamos un nodo raíz y como nodos de transformación para él establecemos nodos de transformación transform1 y transform2

 osg::ref_ptr<osg::Group> root = new osg::Group; root->addChild(transform1.get()); root->addChild(transform2.get()); 

Crear un visor y pasarle el nodo raíz como datos de escena

 osgViewer::Viewer viewer; viewer.setSceneData(root.get()); 

Ejecutar el programa da esa imagen



La estructura del gráfico de escena en este ejemplo es la siguiente.



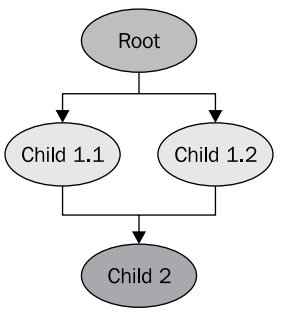
No debemos confundirnos por el hecho de que los nodos de transformación (Niño 1.1 y Niño 1.2) se refieren al mismo objeto hijo del modelo de avión (Niño 2). Este es un mecanismo OSG normal, cuando un nodo secundario de un gráfico de escena puede tener varios nodos principales. Por lo tanto, no tenemos que almacenar dos instancias del modelo en nuestra memoria para obtener dos planos idénticos en la escena. Este mecanismo le permite asignar memoria de manera muy eficiente en la aplicación. El modelo no se eliminará de la memoria hasta que se haga referencia a él como un hijo, al menos un nodo.

En su acción, la clase osg :: MatrixTransform es equivalente a los comandos de OpenGL glMultMatrix () y glLoadMatrix (), implementa todo tipo de transformaciones espaciales, pero es difícil de usar debido a la necesidad de calcular la matriz de transformación.

La clase osg :: PositionAttitudeTransform funciona como las funciones de OpenGL glTranslate (), glScale (), glRotate (). Proporciona métodos públicos para convertir nodos secundarios:

1. setPosition (): mueve el nodo a un punto dado en el espacio especificado por el parámetro osg :: Vec3
   
2. setScale (): escala el objeto a lo largo de los ejes de coordenadas. Los factores de escala a lo largo de los ejes correspondientes se establecen mediante un parámetro del tipo osg :: Vec3
   
3. setAttitude (): establece la orientación espacial del objeto. Como parámetro, toma el cuaternión de conversión de rotación osg :: Quat, cuyo constructor tiene varias sobrecargas que le permiten especificar el cuaternión directamente (por componentes) y, por ejemplo, a través de los ángulos de Euler osg :: Quat (xAngle, osg :: X_AXIS, yAngle, osg :: Y_AXIS, zAngle, osg :: Z_AXIS) (¡los ángulos se dan en radianes!)
   

7. Cambiar nodos

Considere otra clase: osg :: Switch, que le permite mostrar u omitir la representación de un nodo de escena, dependiendo de alguna condición lógica. Es un descendiente de la clase osg :: Group y atribuye algún valor lógico a cada uno de sus hijos. Tiene varios métodos públicos útiles:

1. AddChild () sobrecargado, como segundo parámetro, toma una clave lógica que indica si se muestra o no este nodo.
   
2. setValue (): establece la clave de visibilidad / invisibilidad. Toma el índice del nodo hijo que nos interesa y el valor clave deseado. En consecuencia, getValue () le permite obtener el valor clave actual por el índice del nodo que nos interesa.
   
3. setNewChildDefaultValue (): establece el valor predeterminado para la clave de visibilidad de todos los objetos nuevos agregados como elementos secundarios.
   

Considere la aplicación de esta clase con un ejemplo.


El ejemplo es trivial: cargamos dos modelos: un cessna convencional y un cessna con el efecto de un motor en llamas

 osg::ref_ptr<osg::Node> model1 = osgDB::readNodeFile("../data/cessna.osg"); osg::ref_ptr<osg::Node> model2 = osgDB::readNodeFile("../data/cessnafire.osg"); 

Sin embargo, creamos osg :: Switch como nodo raíz, lo que nos permite, al agregarle modelos como nodos secundarios, establecer la clave de visibilidad para cada uno de ellos.

 osg::ref_ptr<osg::Switch> root = new osg::Switch; root->addChild(model1.get(), false); root->addChild(model2.get(), true); 

Es decir, model1 no se representará y model2 sí, lo cual observaremos al ejecutar el programa



Al intercambiar los valores de las teclas veremos la imagen opuesta

 root->addChild(model1.get(), true); root->addChild(model2.get(), false); 

Levantando ambas teclas, veremos dos modelos al mismo tiempo

 root->addChild(model1.get(), true); root->addChild(model2.get(), true); 

Puede habilitar la visibilidad e invisibilidad de un nodo, un hijo de osg :: Switch, directamente sobre la marcha utilizando el método setValue ()

 switchNode->setValue(0, false); switchNode->setValue(0, true); switchNode->setValue(1, true); switchNode->setValue(1, false); 

Conclusión

En este tutorial, analizamos todas las clases principales de nodos intermedios utilizados en OpenSceeneGraph. Por lo tanto, colocamos otro ladrillo básico en la base del conocimiento sobre el dispositivo de este motor gráfico indudablemente interesante. Los ejemplos discutidos en el artículo, como antes, están disponibles en mi repositorio en Github .

Continuará ...