Lógica difusa contra PID. Cruzamos el erizo y la serpiente. Motor de aeronave y algoritmos de control de NPP

Probablemente, todos los que estudiaron la teoría del control automático en repetidas ocasiones tenían dudas sobre cómo estas dos, tres o incluso diez cuadrados de funciones de transferencia en el modelo representan la dinámica de una unidad compleja, como un reactor nuclear o un motor de avión. ¿Hay trampa aquí? Es posible que trabajar con modelos simples deje de funcionar con modelos complejos en la vida "real".

En este artículo, experimentaremos con el modelo de motor de avión "real". Habiéndolo rodeado de modelos "reales" de equipos y algoritmos de control de una planta de energía nuclear.

Inicialmente, el modelo fue escrito en Fortran y está destinado a algunos fines altamente científicos relacionados con los sistemas de gestión del motor. Este modelo se nos dio como ejemplo y nuestra tarea consistía en repetir el modelo de forma estructural y demostrar que coincide con el original. Lo cual fue hecho.

Tan pronto como el modelo pasó de la lista de Fortran a un diagrama de bloques, se volvió simple y conveniente trabajar con él, realizando cualquiera de los experimentos más "sofisticados". No es casualidad que resulte ser algoritmos reales de control de NPP. Eso hizo posible ensamblar rápidamente un modelo para experimentos sin usar ninguna fórmula, sí, solo imágenes.

Modelo de motor

El modelo es un conjunto de bloques típicos configurados para simular varios componentes de un motor en particular. En un artículo anterior, desmontamos un motor de turbina de gas en el que se elimina la potencia neta utilizando un eje. En un motor turborreactor, la potencia neta es el empuje del chorro, pero controlaremos la velocidad.

El esquema general del modelo se muestra en la Figura 1.

Figura 1. Diagrama de un modelo estructural de un motor turborreactor.

A pesar de que el diagrama del modelo parece una dispersión de partes tridimensionales, de hecho es un conjunto de elementos estructurales interconectados.

Como experimento, nosotros, como en el artículo anterior , intentaremos controlar el suministro de combustible para obtener la velocidad deseada.

Para hacer esto, necesitamos una cámara de combustión, en cuyas propiedades encontremos el consumo de combustible, que cambiaremos. Y en los parámetros, la cámara tiene una presión de entrada, que se calcula en este bloque. (ver fig. 2 y 3)

Figura 2. Propiedades de la cámara de combustión.

Figura 3. Parámetros de la cámara de combustión.

Como velocidad ajustable, tomamos las revoluciones del eje de baja presión. Me parece que sus revoluciones tienen una dependencia más compleja de la presión de suministro de combustible que las revoluciones del eje de alta presión, que se ve afectado por los gases después de la cámara de combustión.

Modelo de suministro de combustible

En el modelo original, el suministro de combustible se especifica en kg / s, como las condiciones límite para el modelado, en forma de una función tabular del tiempo. Queremos crear un modelo cercano al "real", por lo que utilizaremos la propuesta del artículo anterior y crearemos un modelo hidráulico de suministro de combustible desde una tubería y una electroválvula.

Como modelo, colocaremos una tubería con un diámetro de 10 mm, sobre la cual colocaremos una válvula eléctrica. La presión en un lado de la tubería se establece constante, suponiendo que la bomba de combustible esté trabajando allí. La presión del otro lado se tomará del modelo del motor. Al final de la tubería agregamos un estrechamiento de 2 veces para simular la boquilla. (Fig. 4)

Figura 4. Modelo de suministro de combustible al motor.

El modelo incorpora la dependencia del cambio en la resistencia hidráulica de la válvula en la posición de la válvula.

Dicho modelo nos permitirá tener en cuenta el efecto de la presión en la cámara de combustión sobre el consumo de combustible, proporcionando retroalimentación. Cuando aumentamos el consumo de combustible, aumentamos la presión en la cámara de combustión y, en consecuencia, la diferencia entre la bomba de combustible y la cámara de combustión disminuye, lo que conduce a un menor consumo de combustible .

Los costos de la tubería se determinan resolviendo la ecuación no estacionaria del flujo de fluido, teniendo en cuenta la fricción, la viscosidad, la densidad y otros efectos físicos, cuya descripción tomará un par: tres páginas de fórmulas.

Modelo de gestión

Para simular un sistema de control real, tomaremos el modelo del regulador para suministrar vapor a la turbina desde el proyecto de control de la central nuclear. No solo un PID que nos da la posición de la válvula, sino un modelo honesto que tiene:

1. Modelado del funcionamiento del motor de accionamiento teniendo en cuenta la zona de no sensibilidad, los retrasos, las velocidades de apertura y cierre.
2. FIR (relé de conversión de pulso) es un bloque no lineal que proporciona la conversión de la acción de control en el comando "abrir" y "cerrar".
3. Controlador PID.
4. La inercia del sensor de velocidad.

Para describir todos los bloques y modelos enumerados, necesitará otras ciento cincuenta páginas de texto, así que solo dé las imágenes con una explicación mínima.

Modelo de válvula

Es un modelo del motor y el sistema de control local.

El motor es un integrador complicado que procesa los comandos "abrir" y "cerrar", teniendo en cuenta una velocidad de movimiento dada de posibles impactos, fallas de energía, etc. (ver Fig. 5) A la salida de este bloque, la posición de la válvula se calcula en cada punto de tiempo en la simulación del proceso

Figura 5. Modelo de motor eléctrico

Para controlar el motor eléctrico de la válvula, se utiliza la unidad de control de la válvula (BUK), que proporciona un procesamiento lógico de los comandos entrantes y posibles fallas dadas, y también genera todas las señales necesarias para los sistemas de indicación y control. (ver figura 6)

Figura 6. Modelo de la unidad de control de la válvula (BEECH)

Los diagramas en las Figuras 5-6 son esquemas de biblioteca típicos para modelar centrales nucleares. Estos bloques no son modificados por el usuario, sino que están listos y utilizados para crear algoritmos de control. Los algoritmos de control se crean en forma de hojas. En nuestro caso, la hoja del algoritmo de control de la válvula se presenta en la Figura 7.

La formación directa del comando "abrir" o "cerrar" (Más, Menos) se lleva a cabo en el bloque de conversión de pulsos de relé (FIR). Esta unidad se puede realizar tanto en la "lógica de hierro" (transistores, relés, amplificadores) como en forma de programa.
A la entrada del bloque EPI, se calcula una falta de coincidencia, calculada por el bloque PID en forma de porcentaje de desviación. Según estos datos, la unidad misma genera pulsos "abiertos" o "cerrados" (Más, Menos) para la unidad de control de la válvula. El diagrama de bloques del EPI se muestra en la Figura 8.

El algoritmo de control de velocidad se muestra en la Figura 9.

Como datos iniciales para el cálculo del regulador de presión, se utilizan la velocidad establecida y las lecturas del sensor.

El algoritmo PID en sí se muestra en la Figura 10.

El sensor de velocidad tiene en cuenta el retraso, la inercia y el error del sensor real. El diagrama del modelo del sensor se muestra en la Figura 11.

Figura 7. Algoritmo de control de válvula

Figura 8. Diagrama de bloques FIR

Figura 9. El algoritmo de la perilla de control

Figura 10. Controlador PID

Figura 11. Modelo del sensor

Como podemos ver, el modelo es bastante detallado (más de mil bloques) y no es lineal en absoluto.

Dado que en este experimento estamos explorando la posibilidad misma de optimizar y gestionar sistemas complejos, el detalle del modelo matemático es importante para nosotros desde el punto de vista de su no linealidad y complejidad. Por lo tanto, una combinación tan "salvaje" de un programa de control real de los reguladores de la central nuclear y un modelo de motor "real" constituye la tarea de probar los reguladores con modelos complejos.

• El sistema de control utiliza la siguiente configuración:
• Tiempo de apertura y cierre de la válvula: 10 segundos
• rango de regulación de la velocidad del motor - 1500 - 4000 rpm
• banda muerta para el regulador - 1%

Modelo de ajuste y experimento numérico

El modelo que estamos explorando describe solo el motor. Y todas las acciones de control, como el consumo de combustible, los ángulos de rotación de la paleta guía, los caudales, etc., se configuran en forma de funciones que cambian con el tiempo. Hemos creado un modelo de suministro de combustible "más honesto" y estamos tratando de conectarlo al modelo del motor. El diseño del experimento numérico es el siguiente:

1. llevar el modelo del motor a la velocidad nominal;
2. cambiar el suministro de combustible al sistema de control creado;
3. hacer control de velocidad.

La Figura 12 muestra el circuito de control para realizar un experimento numérico.

Figura 12. Modelo de control numérico del experimento.

El modelo puede funcionar en modo de optimización o en modo de control.

Cuando el modo de optimización está activado, la unidad de optimización funciona; en el modo desactivado, no participa en el cálculo.

Se considera que todos los modelos conectados en un solo paquete intercambian datos sincrónicamente a través de una base de datos de señales. En un proyecto de gestión de facturación, los datos se transfieren de un modelo a otro. En particular, la presión de la cámara de combustión del motor se transmite a la presión en la salida del sistema de combustible, y las revoluciones calculadas del eje de baja presión se transmiten al modelo del sensor para contabilizarlo en el sistema de control.

Para simular la inexactitud de medir la velocidad, se agrega ruido blanco al valor calculado de la velocidad del eje.

La velocidad establecida se transmite a la unidad de optimización. Para monitorear la calidad del transitorio, se utilizan caudales y posiciones de válvulas.

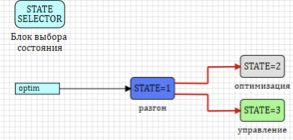
El sistema de control se realiza en forma de una máquina de estados con tres estados (ver Fig. 13):

1. Aceleración del motor. En este estado, el modelo de motor funciona independientemente del sistema de combustible, y el consumo de combustible se establece como una función lineal por partes. El regulador se apaga y las revoluciones calculadas del eje de baja presión se transmiten a las revoluciones establecidas.Dependiendo de la señal del nivel superior, la transición puede ocurrir en el estado de optimización o en el estado de control.
2. Optimización En este estado, el consumo de combustible se toma del modelo hidráulico y se transfiere al modelo del motor. El controlador PID está encendido y ajusta la posición de la válvula. Los coeficientes PID del controlador se toman del bloque de optimización y se aplican al controlador en modo de optimización. Como acción de prueba, se establece un cambio en la velocidad del motor.
3. Gestión. Exactamente lo mismo que la optimización, con la excepción de transmitir los coeficientes al controlador PID.

Figura 13. Máquinas de estado del sistema de gestión del motor.

Figura 14. Los estados "Aceleración del motor" y "Optimización"

El ajuste del controlador se realiza mediante el método de optimización. El diagrama de bloques de optimización se muestra en la Figura 15. Dependiendo de qué unidad de control se use en el sistema para el control, el bloque de optimización selecciona valores para el bloque PID o el bloque de control difuso.

Al configurar, el ruido blanco no se tiene en cuenta (en el bloque se establece como 0).

Figura 15. Bloque de optimización de reguladores

Resultados de la simulación

Para seleccionar los coeficientes del controlador PID, se utiliza el siguiente proceso:

En 10 segundos, la aceleración se realiza utilizando una curva de consumo de combustible calculada previamente. La velocidad de rotación del eje de baja presión al final de la aceleración es de 3564 rpm.

A los 10 segundos del cálculo, la máquina de estado cambia. A partir de este momento, el consumo de combustible se toma del modelo hidráulico, y la frecuencia establecida para el regulador es 3600 rpm.

A los 20 segundos de cálculo, la frecuencia establecida cambia: 3900 rpm.

Por lo tanto, el regulador debe calcular un paso de 36 rpm a 10 segundos de cálculo y un paso de 300 rpm a 30 segundos de cálculo.

El controlador PID sintonizado hace frente con éxito a esta tarea, teniendo en cuenta el hecho de que a los 10 segundos, además de un salto en la velocidad, se produce un salto en el consumo de combustible en el momento de cambiar al modelo hidráulico (ver Fig. 16)

Figura 16. Volcaduras y proceso de control para el controlador PID

Para crear un controlador basado en la lógica difusa y la pureza del experimento, utilizamos el mismo controlador PID ya configurado (ver Fig. 10), en el que agregamos un modelo de controlador basado en la lógica difusa y reemplazamos la salida del controlador; en lugar del PID, enviamos una señal obtenida en lógica difusa .

Por lo tanto, todos los demás parámetros relacionados con la normalización, la zona de insensibilidad, el trabajo del EPI siguen siendo los mismos que para el PID.

La salida del controlador, igual que la salida para el PID, es el porcentaje de falta de coincidencia.
Y dejamos el controlador PID en sí para poder comparar los impactos que dan los reguladores. (ver figura 17)

Figura 17. Conversión de PID a Fuzzy Logic

El regulador en sí se ve igual que en el primer artículo . (ver figura 18). El desajuste se introduce, la primera y la segunda derivada del desajuste se determinan numéricamente y se utiliza una base simple de tres reglas:

• Si menos y disminuye y disminuye la velocidad => disminuir.
• Si la norma es constante y no cambia => no cambie .
• Si más y aumenta y acelera => aumenta .

Figura 18. Diagrama de un controlador difuso.

Para la personalización, utilizamos las mismas variables que utilizamos en el primer artículo : estos son los rangos de desviación de las desviaciones derivadas primera y segunda.

Después de la optimización, comenzamos el mismo proceso de transición.

Figura 19. Volcaduras y controles para lógica difusa
El controlador de lógica difusa funcionó bien. Tenga en cuenta que según la posición de la válvula de compuerta, los pasos "formados por nosotros mismos" se formaron cuando la válvula se detuvo, se detuvo y luego se movió nuevamente.

A juzgar por el horario 19, la lógica difusa manejó el aumento en las velocidades del motor de la aeronave mucho mejor.

Ahora cambiaremos las condiciones del problema sintonizado en el paso positivo de 300 rpm y probaremos el paso negativo de -1500 rpm. (Si toma más, la válvula puede cerrarse, pero no sé cómo se comportará el modelo con un consumo de combustible cero, aunque el motor real permite un apagado a corto plazo del suministro de combustible).

A los 20 segundos de cálculo, establecemos la frecuencia a 2100 rpm. Y veamos cómo funcionan nuestros reguladores. El primero en el ring es Fuzzy Logic.

Figura 20. La práctica de reducir la velocidad. Lógica difusa

El segundo experimento es con un controlador PID. Y que vemos Esta es una falla completa, el controlador PID, sintonizado para aumentar la velocidad, no pudo hacer frente a la disminución de la frecuencia. (ver 21) Algo ahora era alarmante para nuestras centrales nucleares.

El modelo de motor a bajas revoluciones resultó ser completamente incontrolable con la ayuda de un controlador PID sintonizado para controlar a altas revoluciones.

Por cierto, se puede ver que un cierre a corto plazo del suministro de combustible (la válvula se cierra por completo) no conduce al colapso del modelo de motor turborreactor.

Figura 21. La práctica de reducir la velocidad. Controlador PID.

Esto solicita la verificación con el regulador SDA, en el que se utiliza la segunda derivada. Dado que dicho modelo ya se ha hecho para el artículo anterior (ver Fig. 22), convertir la lógica difusa en reglas de tráfico es cuestión de dos segundos. (ver figura 23).

Figura 22. Diagrama estructural de las normas de tránsito del regulador.

Figura 23. Reemplazo de PID con reglas de tráfico en el algoritmo de control

Ajustamos el controlador por el método de optimización y repetimos la reducción de velocidad.

Figura 24 Prueba de la reducción en la velocidad del controlador de reglas de tráfico

SDA trabajó con sobreimpulso, pero claramente mejor que PID, y casi tan bueno como la lógica difusa. Pero hay un exceso!

Vamos a complicar la tarea: agregue ruido al sensor

Ahora intentemos agregar ruido blanco al sensor de medición de señal y ver cómo se comportan los reguladores con el sensor real. La zona muerta es el 1% de la velocidad máxima: 40 rpm. Ajuste el ruido blanco a 50 rpm.

Dado que el PID no funciona a una velocidad menor, realizaremos pruebas a un aumento.

El regulador de control de tráfico claramente no hace frente a ese ruido, aunque mantiene la velocidad requerida, pero la válvula de control tiembla, como en el baile de San Vito, cuando la velocidad establecida está activada. En la Figura 25, la sección 25-26 segundos del proceso está especialmente ampliada.

Figura 25 RPM crecientes con ruido en el sensor. Regulaciones de tráfico

Figura 26 RPM crecientes con ruido en el sensor. Controlador PID

El transitorio para el controlador PID no ha cambiado a pesar del ruido en el sensor de RPM. La gestión viene con pasos claros y largos.

La alarma de la central nuclear retrocedió.

Figura 27. Controlador difuso con ruido en el sensor.

Un controlador con lógica difusa con ruido también controla, pero en los momentos de aplicación a un estado estacionario, se producen fluctuaciones en la posición del organismo regulador.

Conclusiones

La tercera serie de pruebas de lógica difusa contra PID y SDA terminó con una victoria de la lógica difusa. A diferencia del modelo simple del artículo anterior .

Resultó ser imposible controlar el controlador PID a bajas velocidades.

La ventaja identificada experimentalmente de PID es la ausencia de oscilaciones con un sensor ruidoso.

, ( ) .