Hay una serie de tareas en las que una señal de larga duración se divide en segmentos, cada uno de los cuales se procesa por separado. En particular, este enfoque se utiliza para analizar la señal utilizando la transformación de Fourier de ventana, o viceversa, en la síntesis; así como en el procesamiento espectral, como la eliminación de ruido, el cambio de tempo, el filtrado no lineal, la compresión de datos de audio y otros.

El proceso de partición en sí mismo se representa matemáticamente mediante la multiplicación por alguna función de peso ( ventana ) con un desplazamiento. Para la ventana más simple, rectangular, podría verse así:

Señal de origen:



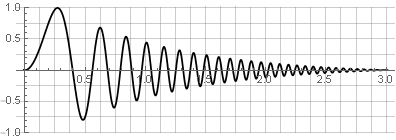
Particiones:







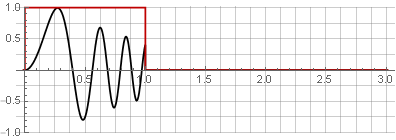
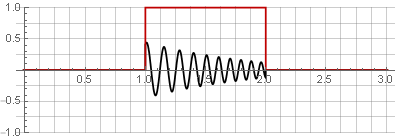
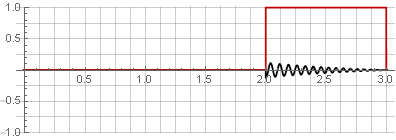
Puede restaurar la señal original simplemente agregándolas.

Más detalles

Sin embargo por Por varias razones, una función rectangular no es la mejor función de ventana. En el análisis espectral, a través de la transformada de Fourier discreta (generalmente rápida), el bloque de datos analizados parece "en bucle", lo que conduce a una brecha en los bordes y una distorsión del espectro:



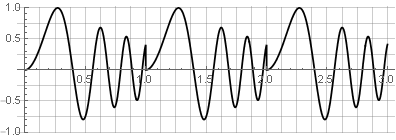
Tampoco es adecuado para la síntesis inversa, ya que cualquier cambio también provocará interrupciones, por ejemplo, si tratamos de invertir una de las partes:



Para eliminar estos inconvenientes, se utiliza la superposición, cuando cada ventana posterior captura parte de los datos de la anterior; y la ventana de peso, respectivamente, cae gradualmente a los bordes.

Superposición al 50%

La mayoría de las veces usan la ventana Hannah (también conocida como "coseno elevado") con una superposición del 50%:








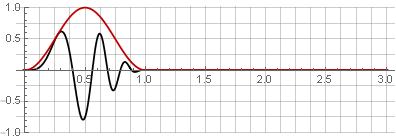
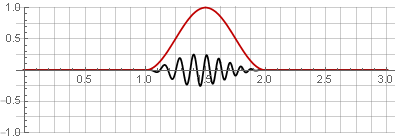
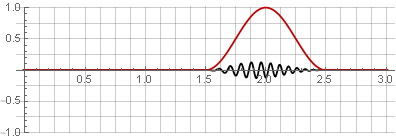
Debido a la simetría de la función coseno durante la suma, se suman a la unidad:



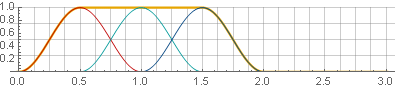
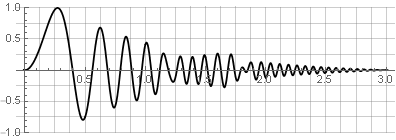
Ahora, con la síntesis inversa, no obtendremos huecos, pero solo a condición de que en los bordes de la ventana los valores sigan siendo cero. Por ejemplo, al invertir una de las partes, no se violará la suavidad:

Procesamiento de doble superposición

Considere con más detalle el algoritmo para procesar una señal usando la transformación rápida de Fourier (FFT):

1. dividir la señal en segmentos con una ventana superpuesta;
2. FFT directa;
3. procesamiento de espectro;
4. FFT inversa;
5. ventana repetida superpuesta (porque después de la FFT inversa, los bordes no necesariamente se acoplarán a cero sin romperse);
6. suma de los segmentos resultantes.

Además, si no se realiza el procesamiento del espectro, la señal de salida debe ser idéntica a la señal de entrada (solo con un retraso de tiempo inevitable).

Cuando se usa la ventana Hann, la superposición del 50% ya no es suficiente, ya que se producirán caídas:



Dado que la doble superposición equivale a la cuadratura, la solución obvia sería utilizar la raíz de la ventana de Hann para compensar la cuadratura:



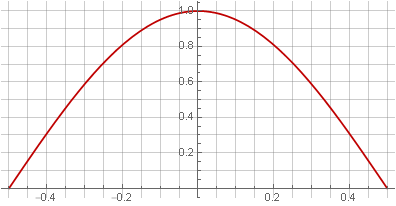
En este caso, sin embargo, la ventana dejó de ser lisa en los bordes; apareció una brecha en la primera derivada.


Puede ir hacia otro lado: use la superposición del 75%, y luego las ventanas también se sumarán en una constante, solo que no en $$$1$ y en $$$\ frac {3} {2}$ :



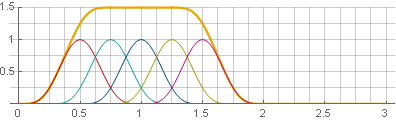
En este caso, tuvimos suerte. Si expandimos el cuadrado a la suma, entonces podemos ver que es una composición de dos ventanas Hannah, pero a diferentes escalas, lo que nos permite cumplir con los requisitos que necesitamos:

$$

$$\ left (\ frac {\ cos (2 \ pi x) +1} {2} \ right) ^ 2 = \ frac {\ cos (2 \ pi x) +1} {2} + \ frac {\ cos (4 \ pi x) -1} {8}$$

Con otras funciones de ventana, tal truco no funcionará; Además, no todas las funciones de ventana estándar pueden proporcionar una suma constante incluso al 50% de superposición.

Idea

Podemos considerar la ventana de Hann no como una función independiente, sino como la diferencia entre dos funciones continuas por partes (se dedicó un artículo separado a una discusión detallada de ellas) con un desplazamiento. Por ejemplo, usando la siguiente función

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ \ sin \ left (\ frac {\ pi x} {2} \ right) & -1 <x <1 \\ \ end {array} \ right.$$

puede escribir

$$

$$f (x + 1) -f (x-1)$$

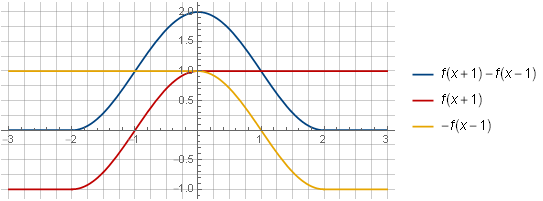
Habiendo considerado los componentes de la suma de dos de esas ventanas, su capacidad de resumir en una constante será más visual:



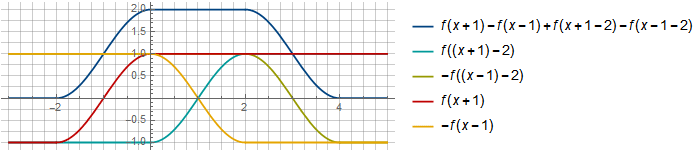
En el segmento $$$[0,2]$ recibimos compensación mutua además de funciones $$$-f (x-1)$ y $$$f ((x + 1) -2)$ desde $$$f ((x + 1) -2) = f (x-1)$

Puede elegir otro desplazamiento, con más superposición, por ejemplo:

$$

$$f \ left (x + \ frac {1} {2} \ right) -f \ left (x- \ frac {1} {2} \ right)$$

Y luego, al cambiar de pasos $$$\ frac {1} {2}$ , también se sumarán en una constante:



Se puede ver que si reorganiza los componentes de la función de ventana, obtendrá las mismas ventanas de Hann.

Por lo tanto, utilizando diferentes funciones de restricción, es posible formar ventanas con la forma requerida.

Fórmula final

Ahora solo queda establecer la escala para que las áreas y valores de definición no dependan de la cantidad de superposición. Definir una ventana en un intervalo $$$[0,1]$ tenemos

$$

$$\ frac {f \ left (\ frac {2 tx} {t-1} -1 \ right) -f \ left (\ frac {2 t (x-1)} {t-1} +1 \ right) } {2}$$

donde $$$f$ - función continua por partes de la forma

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ g (x) & -1 <x <1 \\ \ end {array} \ derecho.$$

pero $$$g$ - alguna función de interpolación entre puntos $$$(- 1, -1)$ y $$$(1,1)$ .

Parámetro $$$t$ determina el nivel de superposición: un divisor que determina el paso por el cual se debe cambiar cada ventana siguiente, $$$x_ {n + 1} = x_n + \ frac {1} {t}$ , y debe ser mayor que uno, $$$t> 1$ .

Porcentaje de superposición $$$p$ puede ser calculado por la fórmula

$$

$$p = \ frac {100 (t-1)} {t}$$

y viceversa

$$

$$t = \ frac {100} {100-p}$$

La apariencia final de la ventana dependerá tanto de la elección del nivel de superposición como de la elección de la función de limitación.

Algunos ejemplos interesantes

Aquí veremos algunas soluciones listas para usar, para las cuales todo se inició. Por simplicidad, consideramos una función de interpolación simple $$$g (x)$ , sin ningún otro fleje.

Ventanas polinomiales

Son los menos costosos computacionalmente. Usando la fórmula derivada previamente

$$

$$\ frac {2 x \ Gamma \ left (n + \ frac {1} {2} \ right) \, _2F_1 \ left (\ frac {1} {2}, 1-n; \ frac {3} {2} ; x ^ 2 \ right)} {\ sqrt {\ pi} \ Gamma (n)}$$

obtenemos un polinomio con un número dado de ceros en derivados más altos que proporcionan la suavidad necesaria de la ventana en los bordes.


Con una superposición del 75% de la ventana con diferentes valores de n, las ventanas se verán así:



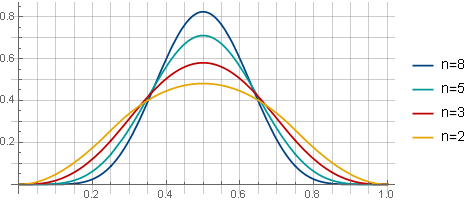
Y en el caso de la extracción de raíz, de esta manera (cuando se usa una superposición del 75%):



más o menos (cuando se usa una superposición del 50%):

La ventana más suave

Función

$$

$$\ tanh \ left (\ frac {k x} {\ sqrt {1-x ^ 2}} \ right)$$

Es interesante porque es infinitamente diferenciable y todas sus derivadas en los bordes son 0 (lo cual puede probarse considerando sus derivadas sobre la base de reglas de diferenciación; en cada término habrá un factor de reducción a cero). Esto nos permite construir ventanas sobre la base, todos los derivados de los cuales no tienen huecos:

Vista de la ventana "falda"

La necesidad de este tipo de ventana está causada por el aumento de la resolución FFT, pero al reducir el efecto del efecto de "incertidumbre de frecuencia de tiempo" a altas frecuencias al aumentar su concentración en el centro.

Primero, determinamos el tipo deseado de función de ventana, por ejemplo, de la siguiente manera:

$$

$$- \ log \ left (k ^ 2 x ^ 2 + 1 \ right) + \ log \ left (k ^ 2 + 1 \ right) - \ frac {k ^ 2 \ left (1-x ^ 2 \ right) } {k ^ 2 + 1}$$

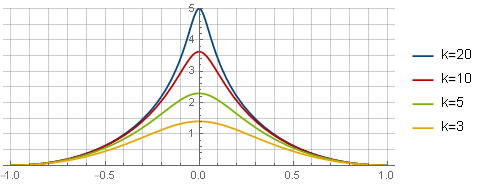
Aquí, el primer término determina la forma de la función en sí, el segundo: proporciona la intersección con el eje de abscisas, el tercero (parábola) restablece la derivada en los bordes para un acoplamiento suave; y el parámetro $$$k$ define la "nitidez" del pico. De esta forma, aún no es adecuado para su uso; primero debe obtener la función de restricción a través de la integración y el escalado:

$$

$$\ frac {kx \ left (k ^ 2 \ left (x ^ 2 + 3 \ right) +6 \ right) +3 \ left (k ^ 2 + 1 \ right) \ left (kx \ left (\ log \ left (k ^ 2 + 1 \ right) - \ log \ left (k ^ 2 x ^ 2 + 1 \ right) \ right) -2 \ tan ^ {- 1} (kx) \ right)} {4 k ^ 3-6 \ left (k ^ 2 + 1 \ right) \ tan ^ {- 1} (k) +6 k}$$

Para mayor comodidad, puede vincular el parámetro $$$k$ al nivel de superposición $$$t$ - por ejemplo, para que la cuarta derivada en el centro de la ventana sea 0 - y luego $$$k$ será considerado como $$$\ sqrt {3} (t-1)$ :



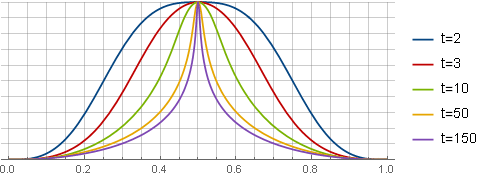
Aquí, para mayor claridad, todas las ventanas se reducen a la misma escala.

Ventana de vista de aguja

Es una versión más "agresiva" de la ventana anterior. Se eligió una hipérbole como base, a partir de la cual, a través de transformaciones sucesivas

$$

$$\ frac {1} {x} \ to \ frac {1} {\ sqrt {x ^ 2}} \ to \ frac {1} {\ sqrt {x ^ 2 + 1}} \ to \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left (1-x ^ 2 \ right) ^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

y usando los mismos pasos en forma de integración y escalado obtuve la fórmula

$$

$$\ frac {kx \ left (2 k ^ 2 \ left (x ^ 2-4 \ right) -3 \ right) \ sqrt {k ^ 2 x ^ 2 + 1} + \ left (8 \ left (k ^ 4 + k ^ 2 \ right) +3 \ right) \ sinh ^ {- 1} (kx)} {\ left (8 \ left (k ^ 4 + k ^ 2 \ right) +3 \ right) \ sinh ^ {-1} (k) -3 k \ sqrt {k ^ 2 + 1} \ left (2 k ^ 2 + 1 \ right)}$$

Aquí también puedes vincular el parámetro $$$k$ al nivel de superposición. La solución directa de la ecuación de la cuarta derivada da un resultado engorroso, por lo que solo hacemos la imagen para la ventana anterior en la imagen y semejanza definiendo $$$k$ como $$$k (t-1)$ asegurando así el papel del parámetro $$$k$ como "ajuste fino". En $$$k = 2.22$ Windows se verá así:

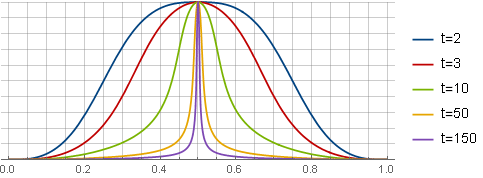
Ventana asimétrica

La función de ventana no tiene que ser simétrica en absoluto. Digamos que necesitamos una ventana con un ataque brusco y una atenuación suave. Podemos obtenerlo de acuerdo con un esquema ya conocido: primero determine la forma deseada de la función, y luego mediante la integración obtenemos la función de restricción. Aquí la tarea es un poco más complicada debido al hecho de que, debido a la asimetría, el centro ya no pasará por el origen, por lo que se agrega un paso de cálculo adicional. Esto también lleva al hecho de que las fórmulas como resultado son bastante engorrosas. Por ejemplo, considere la opción más simple: una parábola multiplicada por una ventana de peso polinomial:

$$

$$(1-x) ^ 2 \ left (1-x ^ {10} \ right) ^ 2$$

Aquí, el grado de x en la ventana ponderada (es decir, 10) determina la "nitidez" del ataque. Utilizamos un valor específico, en lugar de un parámetro simbólico, para simplificar las fórmulas para mayor claridad; si lo desea, puede volver a calcularlo más adelante.

Después de la integración, simplemente el escalado ya no es suficiente; aún necesita alinear los bordes:



Para hacer esto, primero desplazamos la función hacia arriba para alinear el borde izquierdo, y luego la escalamos a dos en el borde derecho y restamos uno. Luego obtenemos la siguiente fórmula:

$$

$$\ frac {8775 \ left (\ frac {x ^ {27}} {27} - \ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25} - \ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14} - \ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ right)} {9856} -1$$

Para que la ventana final tenga la apariencia deseada, también es necesario proporcionar un nivel de superposición suficientemente grande:

Conclusión

Del mismo modo, puede construir ventanas desde cualquier otra función con forma de campana, por ejemplo, gaussianas; y también puede modificar los que ya se consideran para proporcionar una mayor suavidad o cambiar la forma de la curva.

Fuera de consideración, la composición espectral de tales funciones de ventana se mantuvo; se deberían dedicar estudios separados a esto.

Aquí se puede descargar una versión un poco más avanzada del artículo (con la capacidad de cambiar dinámicamente los parámetros en las ventanas bajo consideración y las fórmulas ocultas) en forma de un documento de Wolfram Mathematica.