¿Cuántos programadores necesitas para soportar código escrito previamente?

Hace algún tiempo, tuve lugar una conversación entre mi amigo y yo, en la que sonaron las siguientes frases:

- El número de programadores crecerá constantemente, porque la cantidad de código está creciendo y cada vez se necesitan más desarrolladores para admitirlo.
- Pero el código está envejeciendo, parte de él está dejando soporte. No se descarta la presencia de algún tipo de equilibrio.

Al recordarlos unos días después, me preguntaba si el soporte de código, que requería más y más recursos a lo largo del tiempo, podría paralizar el desarrollo de nuevas funcionalidades o requeriría un aumento ilimitado en el número de programadores. El análisis matemático y las ecuaciones diferenciales ayudaron a evaluar cualitativamente la dependencia del volumen de apoyo del desarrollo y a encontrar respuestas a las preguntas.

La primera pregunta ¿Puede apoyar "comer" todos los recursos de desarrollo?

Considere un equipo de programadores en el que el número de participantes es constante. Parte de su tiempo de trabajo $$$\ mu (t)$ ( $$$0 <\ mu (t) <1$ ) recae en el desarrollo de un nuevo código y la fracción restante del tiempo $$$1- \ mu (t)$ va a apoyar. Bajo los supuestos del modelo, suponga que el primer tipo de actividad está dirigido a aumentar la cantidad de código, y el segundo, a cambiarlo (corregir errores) y no afecta significativamente la cantidad de código.

Denotamos $$$y (t)$ todo el código escrito por tiempo $$$t$ . Teniendo en cuenta que la velocidad de escribir código es proporcional $$$\ mu (t)$ obtenemos:

$$

$$\ frac {dy (t)} {dt} = a_0 \ mu (t); a_0 \ in \ mathbb {R}, a_0> 0.$$

Es natural suponer que el trabajo involucrado en el mantenimiento del código es proporcional a su volumen:

$$

$$1- \ mu (t) = a_1 y (t); a_1 \ in \ mathbb {R}, a_1> 0$$

o

$$

$$\ mu (t) = 1-a_1y (t)$$

De donde

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1y (t))).$$

Obtenemos una ecuación diferencial que se integra fácilmente. Si en el momento inicial la cantidad de código es cero, entonces

$$

$$y (t) = \ frac {1} {a_1} (1-e ^ {- a_0a_1t}).$$

En $$$t \ to + \ infty$ funcion $$$y (t) \ to1 / a_1$ y $$$\ mu (t) \ a 0$ . Y esto significa una reducción gradual en el tiempo del desarrollo de nuevas funcionalidades a cero y la transición de todos los recursos para el soporte.

Sin embargo, si a tiempo $$$h> 0$ Dado que el código se vuelve obsoleto y deja de ser compatible, la cantidad de código que requiere soporte a la vez $$$t$ igual a $$$y (t) - y (t-h).$ Entonces

$$

$$1- \ mu (t) = a_1 (y (t) - y (t-h)),$$

$$

$$\ mu (t) = 1-a_1 (y (t) - y (t-h)),$$

pero $$$y (t)$ es una solución de una ecuación diferencial con un argumento retrasado [1]:

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1 (y (t) - y (t-h))).$$

La solución a esta ecuación se determina de manera única estableciendo los valores $$$y (t)$ "Antes del comienzo de los tiempos", con $$$t \ en [-h, 0]$ . Como no se escribió ningún código antes de la hora inicial, en nuestro caso $$$y (t) = 0$ a las $$$t \ en [-h, 0]$ .

Veamos algunos ejemplos. Mediremos el tiempo en años y la cantidad de código en miles de líneas. Entonces por $$$a_0$ Los valores del orden de las decenas son aceptables, tomamos 50 y 100. Es decir, en un año el equipo de desarrollo escribirá cincuenta y cien mil líneas de código, respectivamente. Para $$$a_1$ Los valores aceptables pueden ser: $$$0.25 / a_0$ , $$$0.5 / a_0$ , $$$1 / a_0$ . Esto significa que el equipo de desarrollo puede mantener la cantidad de código que escribió para el año, con un trimestre, la mitad o la carga de trabajo completa. Como tiempo promedio de vida del código, establezcamos los valores: 1, 2 y 4 años. Resolviendo la ecuación numéricamente, obtenemos ejemplos del comportamiento de la función. $$$\ mu (t)$ para algunas combinaciones de parámetros $$$h, a_0, a_1$ .

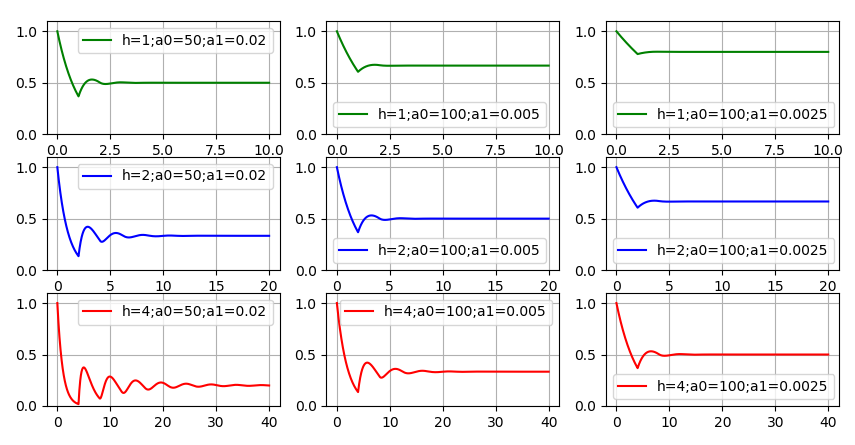
Comportamiento de la función $$$\ mu (t)$ ante el envejecimiento, el código ha cambiado. La función ha dejado de ser monótona, pero las fluctuaciones se "calman" con el tiempo, hay una tendencia hacia $$$\ mu (t)$ a algún valor constante. Gráficos muestran: cuanto más $$$h$ , $$$a_0$ y $$$a_1$ , es decir, cuanto más lento sea el código, más rápido se desarrollará el nuevo código y menor será la calidad del código, menos recursos quedarán para el desarrollo de una nueva funcionalidad. Hubo un deseo de dar al menos un ejemplo en el que $$$\ mu (t)$ "Acurrucado" cerca de cero. Pero esto requería la selección de indicadores de calidad de desarrollo muy pobres y un código antiguo. Incluso en el gráfico inferior izquierdo, queda una cantidad significativa de recursos para la nueva funcionalidad. Por lo tanto, la respuesta correcta a la primera pregunta es más probable: teóricamente, sí, es posible; prácticamente, apenas.

Preguntas que no pudieron ser respondidas:

1. Es cierto que $$$\ mu (t)$ tiende a un cierto límite para $$$t \ to + \ infty$ para todos $$$a_0, a_1> 0$ ? Si no es para todos, ¿para qué?
2. Si el límite existe, entonces cómo depende su valor $$$a_0, a_1$ ?

La segunda pregunta. ¿Puede el soporte de código causar un crecimiento ilimitado en el número de programadores?

Denotamos $$$q (t)$ Número de programadores involucrados en el desarrollo de un nuevo código. Como arriba $$$y (t)$ - la cantidad de código escrito por el momento $$$t$ . Entonces

$$

$$\ frac {dy (t)} {dt} = a_2 q (t); a_2 \ in \ mathbb {R}, a_2> 0.$$

Deje que el código soporte ocupado $$$p (t)$ programadores Envejecimiento del código C

$$

$$p (t) = a_3 (y (t) -y (t-h)); a_3 \ in \ mathbb {R}, a_3> 0.$$

De donde

$$

$$p (t) = a_3 \ int_ {t-h} ^ {t} \ frac {dy (s)} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq (s) ds.$$

Si $$$q (t) \ leq C_1$ entonces

$$

$$p (t) \ leq a_1a_2C_1h.$$

Por lo tanto, la respuesta a la segunda pregunta es negativa: si el número de desarrolladores de código nuevo es limitado, entonces, en el contexto del código antiguo, el soporte no puede causar un aumento ilimitado en el número de programadores.

Conclusión

Los modelos considerados son modelos matemáticos "blandos" [2]. Son muy simples. Sin embargo, la dependencia de los resultados de la simulación con los valores de los parámetros corresponde a la esperada para los sistemas reales; esto habla a favor de la adecuación de los modelos y la precisión suficiente para obtener estimaciones cualitativas.

Referencias

1. Elsgolts L.E., Norkin S.B. Introducción a la teoría de ecuaciones diferenciales con argumento diferente. Moscú Editorial "Ciencia". 1971
2. Arnold V.I. Modelos matemáticos "duros" y "blandos". Moscú Editorial del Centro. 2004