¿Qué evidencia puede convencer a los matemáticos si no hay evidencia rigurosa?

El nuevo modelo estadístico parece socavar las suposiciones aceptadas desde hace mucho tiempo de la teoría de números. ¿Cuánto puede confiar en ella si solo la evidencia rigurosa realmente importa?

¿Qué puntos de la curva elíptica y ² = x ³ - 4x + 1 son racionales? Para encontrarlos, necesita dibujar líneas a través de pares de puntos racionales. Todos los puntos a través de los cuales pasan las líneas también serán racionales.

Recientemente, cuatro investigadores han ideado un modelo que da vuelta el sentido común de su campo de investigación. Utilizaron datos computacionales para sugerir que la visión predominante de varias décadas de uno de los conceptos fundamentales era errónea.

Y estos no son biólogos, climatólogos o físicos. En su campo científico, los modelos empíricos no tienen voz en relación con la verdad. Son matemáticos, representantes de la disciplina, cuya moneda estándar, una prueba lógica innegable, generalmente los salva de los debates que afectan a otras áreas. Y, sin embargo, aquí están, con su modelo diciendo que probablemente es hora de revisar algunas de las ideas de larga data.

Un modelo publicado en línea en 2016 y listo para aparecer en el Journal of the European Mathematical Society pertenece a un concepto matemático tan venerable como el rango de una ecuación algebraica. El rango es una medida que corresponde a cuántas soluciones de la ecuación se relacionan con los números racionales y cuáles con los irracionales. Las ecuaciones de alto rango tienen soluciones más racionales y son más complicadas.

Desde principios del siglo XX, los matemáticos se han interesado en la cuestión de si existen restricciones en la altura del rango de la ecuación. Al principio, casi todos pensaron que la restricción debería existir. Pero en la década de 1970, la opinión predominante había cambiado: la mayoría de los matemáticos comenzaron a creer que el rango era ilimitado, lo que significa que es posible detectar curvas con rangos infinitamente grandes. Así sucedió, aunque algunos matemáticos creían que no había argumentos sólidos en apoyo de esta opinión.

“La gente es muy autoritaria sobre la ausencia de restricciones. Sin embargo, cuando comienzas a entender, resulta que la evidencia de esto es extremadamente débil ”, dijo Andrew Granville , matemático de la Universidad de Montreal y el University College London.

Hoy, la evidencia sugiere lo contrario. Dos años después de la aparición del modelo, convenció a muchos matemáticos de que el rango de ecuaciones algebraicas de cierto tipo era realmente limitado. Sin embargo, no todos piensan que este modelo sea convincente. La falta de acuerdo plantea preguntas que a menudo no están relacionadas con los resultados matemáticos: ¿qué peso puede tener la evidencia empírica en un área en la que solo importan las pruebas rigurosas?

"No hay justificación matemática de que este modelo sea exactamente lo que necesitamos", dijo Jennifer Park , matemática de la Universidad de Ohio, coautora del trabajo. "Además, desde un punto de vista experimental, muchas cosas funcionan".

Punto a punto

Si se le da una ecuación, puede dibujar una curva de sus soluciones en el gráfico. Los matemáticos quieren saber cuántas de estas soluciones son racionales: pertenecen al tipo de números, que se pueden expresar como la razón de dos enteros (1/2, -3 o 4483/929).

Las soluciones racionales son difíciles de encontrar sistemáticamente, pero los matemáticos tienen técnicas que funcionan bajo ciertas condiciones. Tome la ecuación x ² + y ² = 1. La gráfica de soluciones a esta ecuación es un círculo. Para encontrar todos los puntos racionales del círculo, comenzamos con una solución definida, digamos, desde el punto en el que x = 1 e y = 0. Luego dibuja una línea a través de este punto que intersecte el círculo en otro punto. Si la pendiente de nuestra línea es racional, entonces el segundo punto de intersección también será una solución racional. Al trazar una línea, aumentamos el número de decisiones racionales de uno a dos.



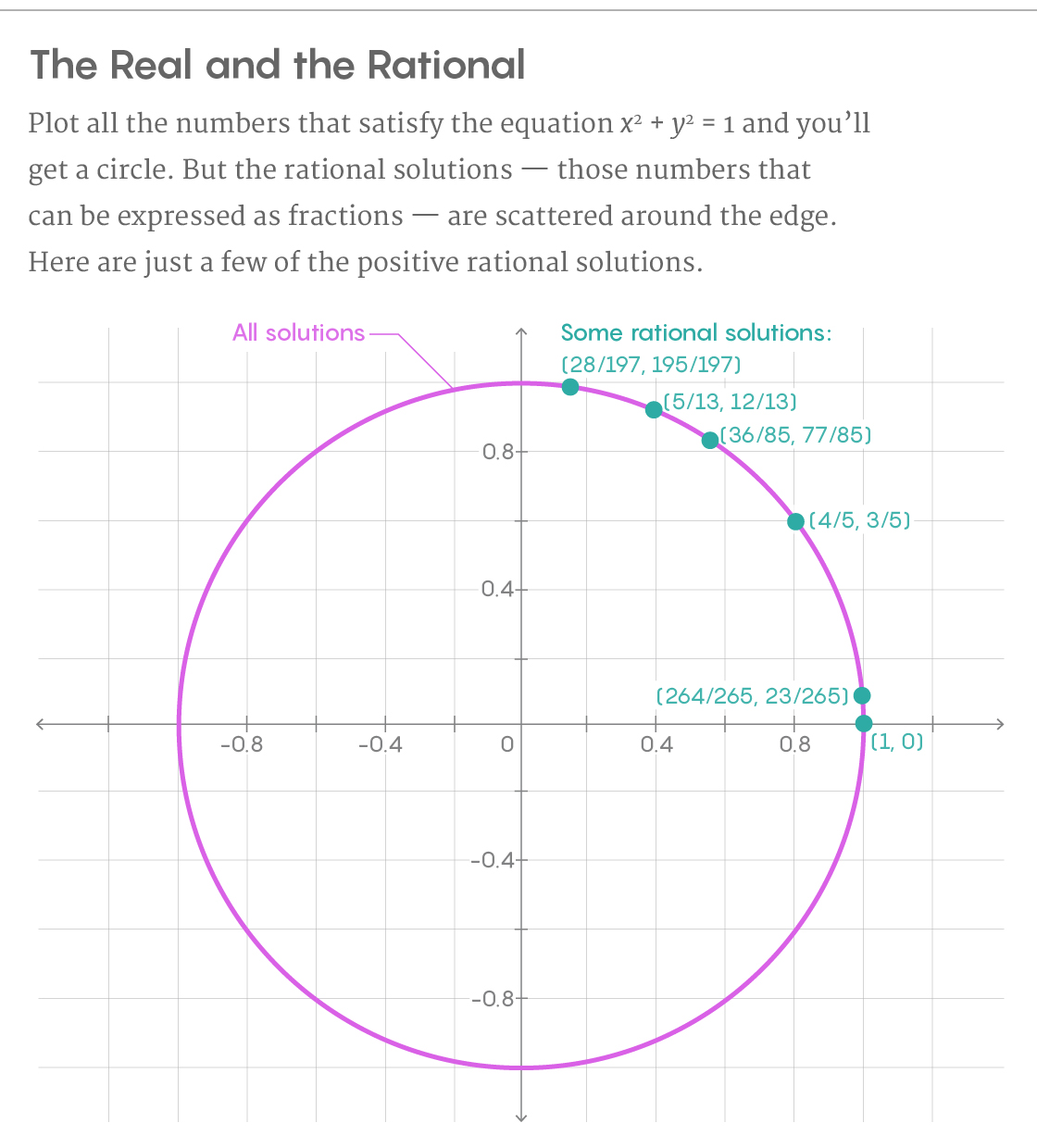
Y no hay necesidad de detenerse allí. Repetimos el procedimiento dibujando una línea recta con otra pendiente racional a través del segundo punto racional: intersecta el círculo en el tercer punto racional. Continuando de esta manera hasta el infinito, eventualmente encontraremos todos los puntos racionales del círculo, de los cuales hay un número infinito.

Y en el caso de un círculo, debe comenzar desde un solo punto, y puede encontrarlos todos. El número de decisiones racionales que necesita saber al principio para encontrar todas las demás se conoce como el rango de la curva. El rango es una forma ordenada de describir un conjunto infinito de decisiones racionales en un solo número. "Es como la mejor manera de describir las soluciones racionales a estas curvas", dijo Bjorn Puunen , matemático del MIT, coautor del modelo, con Park, John Voight del Dartmouth College y Melanie Matchet Wood de la Universidad de Wisconsin.

Un círculo es una ecuación cuadrática, o una ecuación de segundo grado ("grado" significa la magnitud del mayor de los grados de los términos de la ecuación). Durante más de cien años, los matemáticos han sabido encontrar soluciones racionales a las ecuaciones de segundo grado.

El siguiente tipo de ecuaciones son las curvas elípticas, en las que hay variables elevadas al tercer grado. Las curvas elípticas existen en el campo más atractivo de la investigación matemática. Son más complicadas que las ecuaciones de segundo orden, por lo que son interesantes de estudiar, pero no son demasiado complicadas. El procedimiento modificado para dibujar líneas rectas sigue siendo aplicable a las curvas elípticas, pero deja de funcionar con ecuaciones de cuarto orden y superiores.

Las curvas elípticas vienen en diferentes rangos. Con algunas curvas elípticas, puede comenzar desde un punto racional, aplicar el procedimiento de dibujar líneas y no encontrar todas las soluciones racionales. Es posible que deba agregar un segundo punto racional que no esté relacionado con el primero. Con él, comenzará un nuevo procedimiento para dibujar líneas, y encontrará un equilibrio de puntos racionales. Una curva, para encontrar todos los puntos racionales de los que necesita conocer dos puntos racionales inicialmente, tiene un rango igual a dos.

No hay restricción comprobada en la altura del rango de una curva elíptica. Cuanto mayor es el rango de la ecuación, más amplio y complejo es el conjunto de soluciones racionales de la curva. "El rango de alguna manera mide la complejidad del conjunto de decisiones", dijo Puunen.

Sin embargo, el rango elude los intentos de los matemáticos de describirlo en teoría. Si se le da una curva elíptica, no tendrá una relación obvia entre cómo se ve y cuál es su rango. "Si tengo una curva elíptica y ajusto un poco los coeficientes, entonces su rango cambia radicalmente", dijo Park. - Puedes cambiar el coeficiente en uno, y el rango saltará a un millón. Nadie sabe cómo se comportan las filas ".

La falta de una teoría general llevó a los matemáticos a retirarse al pequeño conjunto de pruebas que tienen para especular sobre la existencia de una restricción de rango. "El punto de vista es que no hay restricciones en el rango, porque la gente todo el tiempo encontró más y más altos rangos", dijo Granville. El poseedor del récord actual es una curva elíptica de rango 28, descubierta en 2006 por Noam Elkis, matemático de la Universidad de Harvard.

Pero luego apareció este nuevo modelo, y declaró que era casi seguro que era el final del camino.

Sorpresa alrededor de los 21

Para estudiar fenómenos que son demasiado complejos o inaccesibles para la investigación directa, los científicos usan modelos. Después de haber creado un análogo de un agujero negro en el laboratorio, pueden aprender algo sobre cómo se comportan los agujeros negros reales, sin tener que caminar por el borde del horizonte de eventos.

Los matemáticos hacen lo mismo. Un buen ejemplo es el estudio de los números primos. Los matemáticos quieren saber la respuesta a la pregunta sobre primos gemelos : ¿hay un número infinito de pares de primos que difieran en 2 (3 y 5, 11 y 13)? Una respuesta exhaustiva va más allá de su conocimiento, pero crearon modelos que predicen la frecuencia de los números gemelos, y la respuesta parece ser que ocurren un número infinito de veces.

El nuevo modelo no estudia directamente las curvas elípticas. Ella explora un objeto matemático como el núcleo de la matriz . Los núcleos se refieren a curvas elípticas, como los ratones a las personas no son lo mismo, pero son más fáciles de estudiar, y se espera que estén lo suficientemente cerca como para sacar conclusiones sobre algunos sobre la base de experimentos en otros. En particular, los núcleos tienen su propia versión de rango . Habiendo estudiado la distribución del rango de núcleos (cuántos núcleos tienen un rango de 1, cuántos núcleos tienen un rango de 2, etc.), cuatro matemáticos esperaban tener una idea de la distribución de los rangos en curvas elípticas. De hecho, apuestan a que la distribución de los rangos de los núcleos y las curvas elípticas son similares entre sí.


Jennifer Park, Bjorn Puunen y Melanie Wood

"El salto de fe entra en juego", dijo Park. "Esperamos que tal vez haya otro conjunto de objetos matemáticos que sea mucho más comprensible y tenga la misma distribución de rango que las curvas elípticas".

Cuando los cuatro investigadores hicieron este trabajo, la mayoría de los matemáticos consideraron que el rango era ilimitado. Sin embargo, el modelo contó una historia diferente. Ella dice que solo hay un número finito de curvas elípticas con un rango de más de 21. Y si hay un número finito de ellas, entonces una de ellas tendrá el rango más alto, lo que significará que el rango todavía tiene un límite superior. Cuando los cuatro matemáticos vieron esto, se dieron cuenta de que tenían un resultado vivo en sus manos.

"Esta predicción no coincidía con lo que todos creían, al menos con lo que admitían públicamente", dijo Wood. "Nadie creía que los rangos pudieran tener una limitación".

Si la fe en el modelo requiere un paso bastante serio, entonces cuando el modelo informa que el sentido común estaba mal, se requiere un paso aún más grande. Sin embargo, mucha evidencia habla a favor de este resultado. Este modelo se basa en modelos anteriores creados por otros matemáticos que han estudiado diversas propiedades de las curvas elípticas. Esos modelos han resistido la prueba del tiempo; Algunas de estas predicciones incluso han sido probadas.

"Nadie sugirió comenzar desde cero y hacer un nuevo modelo", dijo Wood. "La pregunta era cómo enriquecer los modelos existentes en los que la gente ya cree".

Otra razón para creer en el modelo fue que un valor de rango de 21 no parece ser un límite arbitrario. Diez años antes, Granville creó otro modelo, del que también se dedujo que debería haber solo un número limitado de curvas elípticas con un rango superior a 21. El modelo Granville no era en absoluto similar al actual, y el hecho de que ambos dieron el rango 21 como significativo era muy diferente a una simple coincidencia desde el punto de vista de muchos matemáticos.

"Tenemos dos modelos heurísticos completamente diferentes y ambos dieron el mismo número, 21, sorprendió a la gente", dijo Park.

Quizás la razón más convincente de que el modelo parece creíble fue el hecho de que sus otras predicciones coincidían casi exactamente con las propiedades comprobadas de las curvas elípticas. La conclusión generalizada del modelo, la existencia de un número finito de curvas elípticas con un rango de más de 21, se aplica a todas las curvas elípticas. Sin embargo, tienen ciertas familias, para muchas de las cuales los matemáticos ya han determinado los límites de las filas. El modelo también predijo valores de rango para muchas de estas familias, y sus predicciones fueron similares, o incluso coincidieron exactamente con los límites que los matemáticos ya han determinado.

"Nuestras fronteras predijeron con precisión todos los casos que fueron estudiados por otras personas", dijo Park. "La gente es escéptica sobre mis informes, pero cuando menciono otras coincidencias, se sorprenden mucho de esto".

Entre evidencia y evidencia

El modelo tiene mucho apoyo, pero no todos lo creen, y puede resultar incorrecto. El escéptico más importante es Noam Elkis, un matemático de Harvard que estableció un récord de rango para una curva elíptica. En las décadas transcurridas desde que se convirtió en el profesor a tiempo completo más joven en Harvard, ha recibido varios resultados que indican la ausencia de un límite de rango. "Mi opinión no ha cambiado durante mucho tiempo. No creo que estemos bien versados ​​en este tema para apoyar esta o aquella hipótesis", me escribió Elkis por correo.

Elkis cree que el modelo puede no funcionar correctamente de muchas maneras. Tiene en cuenta las curvas seleccionadas al azar, o las curvas en algún sentido son promedio. Sin embargo, existe evidencia, incluida la investigación realizada por el propio Elkis, sobre la posibilidad de la existencia de familias de curvas elípticas, cada una de las cuales incluye un número infinito de tales curvas, cuyo comportamiento difiere significativamente del comportamiento de las curvas típicas. "Los modelos heurísticos basados ​​en el comportamiento esperado de curvas aleatorias pueden no contar toda la historia sobre el comportamiento extremo", escribe Elkis.

Incluso uno de los autores del modelo no está completamente seguro de ello. "Diría que estoy limitado en las filas como un agnóstico", dijo Wood. Ella admite que el modelo puede ser incorrecto por razones expresadas por Elkis. Pero si el modelo no hace frente a la tarea, entonces porque no tuvo en cuenta algunas propiedades ocultas e inesperadas de las curvas elípticas. "La pregunta es: si no crees en los rangos limitados, ¿en qué lugar deja de funcionar el modelo?" - dijo Wood

“Lo más probable es que tengan razón si alguien no encuentra alguna razón ingeniosa por la que están equivocados. No tengo idea de si existe tal razón o no ”, dijo Alexander Smith, un estudiante graduado de Harvard que trabaja con Elkis y estudia las filas de curvas elípticas.

Los autores del modelo no elevan su importancia al dogma. Conocen la diferencia entre evidencia y evidencia, y entienden que ninguna montaña de la primera conducirá a la segunda. Pero creen que su trabajo, como mínimo, proporciona una base razonable para la reflexión sobre conceptos matemáticos básicos después de un siglo de razonamiento simple.

"Quizás encontrar curvas elípticas de orden superior es un desafío para los matemáticos", dijo Park. O, tal vez, los matemáticos "deberían reconsiderar su opinión sobre lo que creíamos, como una hipótesis popular".