Moderna DDR3 SDRAM. Fuente: BY-SA / 4.0 por KjerishEn una visita reciente al
Museo de Historia de la Computación en Mountain View, un antiguo ejemplo de
memoria de
ferrita me llamó la atención.
Fuente: BY-SA / 3.0 por Konstantin LanzetRápidamente llegué a la conclusión de que no tengo idea de cómo funcionan esas cosas. Gire los anillos (no), y por qué pasan tres cables por cada anillo (todavía no entiendo cómo funcionan). Más importante aún, me di cuenta de que tengo muy poca idea de cómo funciona la RAM dinámica moderna.
Fuente: Ciclo de memoria de Ulrich DrapperEstaba particularmente interesado en una de las consecuencias de cómo funciona la RAM dinámica. Resulta que cada bit de datos se almacena por una carga (o su ausencia) en un pequeño condensador en el chip RAM. Pero estos condensadores pierden gradualmente su carga con el tiempo. Para evitar la pérdida de datos almacenados, deben actualizarse periódicamente para restablecer el cargo (si corresponde) a su nivel original. Este
proceso de actualización implica leer cada bit y luego escribirlo de nuevo. Durante esta "actualización", la memoria está ocupada y no puede realizar operaciones normales, como escribir o almacenar bits.
Esto me molestó durante mucho tiempo, y me preguntaba ... ¿es posible notar un retraso en la actualización a nivel de programa?
Base de entrenamiento de actualización dinámica de RAM
Cada DIMM consta de "celdas" y "filas", "columnas", "lados" y / o "rangos".
Esta presentación de la Universidad de Utah explica la nomenclatura. La configuración de la memoria de la computadora se puede verificar con el
decode-dimms . Aquí hay un ejemplo:
$ decode-dimms
Size 4096 MB
Bancos x Filas x Columnas x Bits 8 x 15 x 10 x 64
Rangos 2
No necesitamos comprender todo el esquema DDR DIMM, queremos entender el funcionamiento de una sola celda que almacena un bit de información. Más precisamente, solo estamos interesados en el proceso de actualización.
Considere dos fuentes:
Cada bit en la memoria dinámica debe actualizarse: esto generalmente ocurre cada 64 ms (la llamada actualización estática). Esta es una operación bastante cara. Para evitar una parada importante cada 64 ms, el proceso se divide en 8192 operaciones de actualización más pequeñas. En cada uno de ellos, el controlador de memoria de la computadora envía comandos de actualización a los chips DRAM. Después de recibir las instrucciones, el chip actualizará 1/8192 celdas. Si cuenta, entonces 64 ms / 8192 = 7812.5 ns o 7.81 μs. Esto significa lo siguiente:
- Se ejecuta un comando de actualización cada 7812.5 ns. Se llama tREFI.
- El proceso de actualización y recuperación lleva algún tiempo, por lo que el chip puede volver a realizar operaciones normales de lectura y escritura. El llamado tRFC equivale a 75 ns o 120 ns (como en la documentación mencionada de Micron).
Si la memoria está caliente (más de 85 ° C), el tiempo de almacenamiento de datos en la memoria disminuye y el tiempo de actualización estático se reduce a la mitad a 32 ms. En consecuencia, tREFI cae a 3906.25 ns.
Un chip de memoria típico está ocupado actualizando durante una parte importante de su vida: del 0,4% al 5%. Además, los chips de memoria son responsables de la parte no trivial del consumo de energía de una computadora típica, y la mayor parte de esta energía se gasta en actualizaciones.
Todo el chip de memoria se bloquea durante la actualización. Es decir, cada bit en la memoria está bloqueado durante más de 75 ns cada 7812 ns. Vamos a medirlo
Preparación del experimento
Para medir operaciones con precisión de nanosegundos, necesita un ciclo muy ajustado, tal vez en C. Se ve así:
for (i = 0; i < ...; i++) {
El código completo está disponible en GitHub.El código es muy simple. Realizar lectura de memoria. Volcamos datos del caché de la CPU. Medimos el tiempo
(Nota: en el
segundo experimento, intenté usar MOVNTDQA para cargar datos, pero esto requiere una página especial de memoria no almacenable en caché y derechos de root).
En mi computadora, el programa muestra los siguientes datos:
# marca de tiempo, tiempo de ciclo
3101895733, 134
3101895865, 132
3101896002, 137
3101896134, 132
3101896268, 134
3101896403, 135
3101896762, 359
3101896901, 139
3101897038, 137
Usualmente, se obtiene un ciclo con una duración de aproximadamente 140 ns, periódicamente el tiempo salta a aproximadamente 360 ns. A veces aparecen resultados extraños sobre 3200 ns.
Lamentablemente, los datos son demasiado ruidosos. Es muy difícil ver si hay un retraso notable asociado con los ciclos de actualización.
Transformada rápida de Fourier
En algún momento me di cuenta. Como queremos encontrar un evento con un intervalo fijo, podemos enviar datos al algoritmo FFT (transformación rápida de Fourier), que descifra las frecuencias principales.
No soy el primero en pensarlo: Mark Seaborn con la famosa vulnerabilidad
Rowhammer implementó esta técnica en 2015. Incluso después de mirar el código de Mark, hacer que FFT funcionara fue más difícil de lo que esperaba. Pero al final, puse todas las piezas juntas.
Primero necesitas preparar los datos. FFT requiere una entrada con un intervalo de muestreo constante. También queremos recortar los datos para reducir el ruido. Por prueba y error, descubrí que el mejor resultado se logra después del procesamiento preliminar de los datos:
- Los valores pequeños (menos de 1.8 promedio) de las iteraciones de bucle se cortan, ignoran y reemplazan con ceros. Realmente no queremos hacer ruido.
- Todas las otras lecturas son reemplazadas por unidades, ya que la amplitud del retraso causado por algún ruido realmente no es importante para nosotros.
- Me decidí por un intervalo de muestreo de 100 ns, pero cualquier número hasta la frecuencia de Nyquist (frecuencia doble esperada) servirá .
- Los datos deben ser muestreados en un tiempo fijo antes de ser enviados a la FFT. Todos los métodos de muestreo razonables funcionan bien, me decidí por la interpolación lineal básica.
El algoritmo es algo como esto:
UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )
Lo que en mis datos produce un vector bastante aburrido como este:
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ...]
Sin embargo, el vector es bastante grande, generalmente alrededor de 200 mil puntos de datos. Con tales datos, puede usar FFT!
C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)
Bastante simple, ¿verdad? Esto produce dos vectores:
- C contiene números complejos de componentes de frecuencia. No nos interesan los números complejos, y puede suavizarlos con el comando
abs() . - F contiene etiquetas, cuyo intervalo de frecuencia se encuentra en qué lugar del vector C. Normalizamos el exponente a hertz multiplicando por la frecuencia de muestreo del vector de entrada.
El resultado se puede trazar en un gráfico:
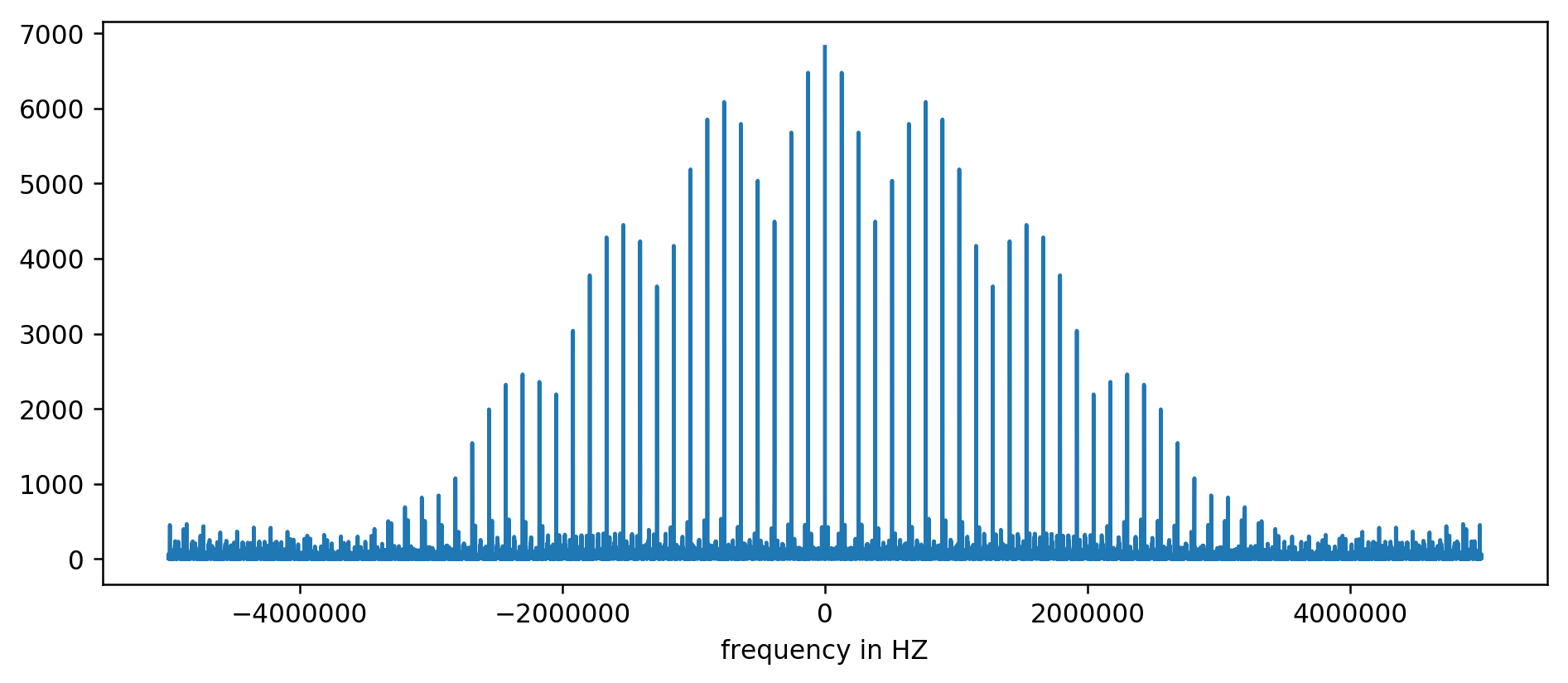
Eje Y sin unidades, ya que normalizamos el tiempo de retraso. A pesar de esto, las ráfagas son claramente visibles en algunos rangos de frecuencia fijos. Consideremos más cerca:
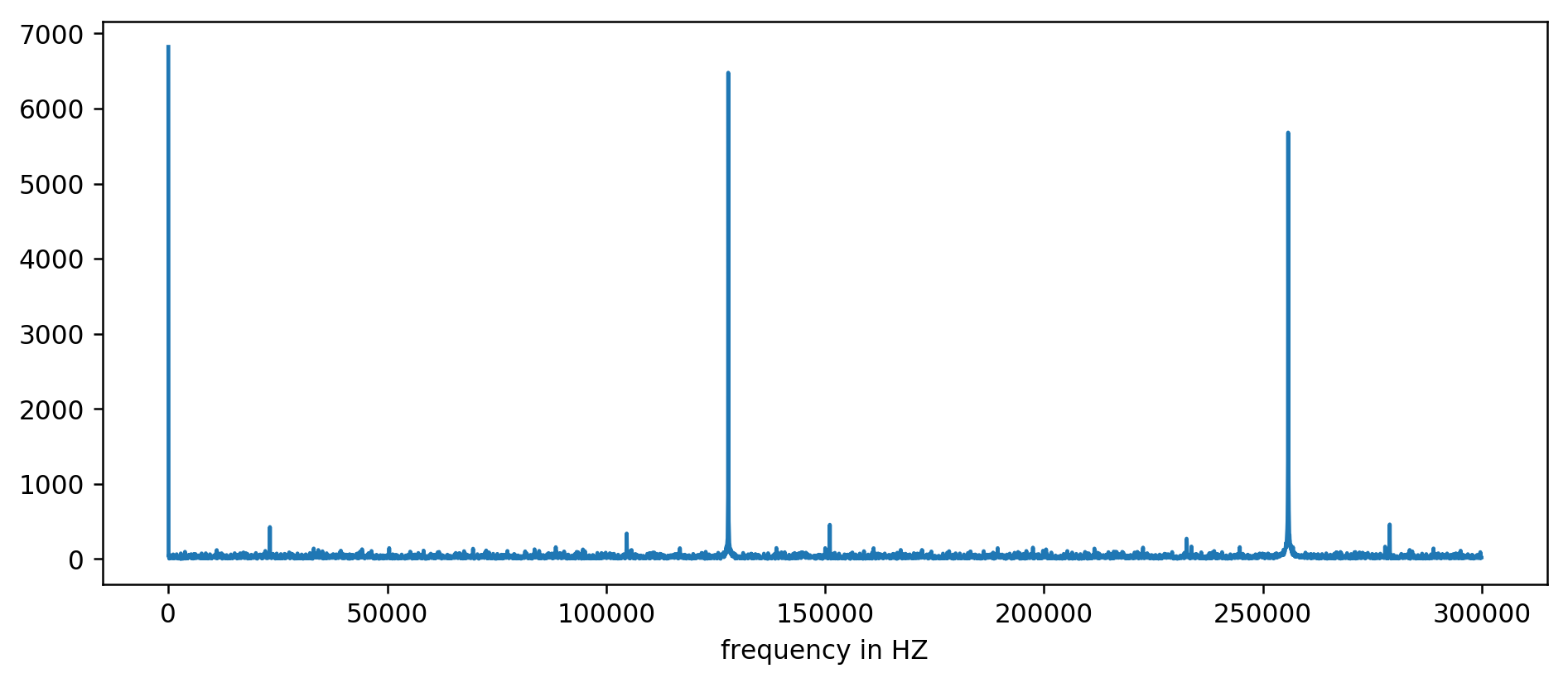
Vemos claramente los primeros tres picos. Después de un poco de aritmética inexpresiva, incluida la lectura de filtrado al menos diez veces el promedio, puede extraer las frecuencias base:
127850.0
127900.0
127950.0
255700.0
255750.0
255800.0
255850.0
255900.0
255950.0
383600.0
383650.0
Consideramos: 1000000000 (ns / s) / 127900 (Hz) = 7818.6 ns
¡Hurra! El primer salto en frecuencia es realmente lo que estábamos buscando, y realmente se correlaciona con el tiempo de actualización.
Los picos restantes a 256 kHz, 384 kHz, 512 kHz son los llamados armónicos que son múltiplos de nuestra frecuencia base de 128 kHz. Este es el efecto secundario totalmente esperado de
aplicar FFT a algo así como una onda cuadrada .
Para facilitar los experimentos, creamos una
versión para la línea de comando . Puede ejecutar el código usted mismo. Aquí hay un ejemplo de inicio en mi servidor:
~ / 2018-11-memory-refresh $ make
gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram
./measure-dram | python3 ./analyze-dram.py
[*] Verificando ASLR: main = 0x555555554890 stack = 0x7fffffefe2ec
[] Dato curioso. Hice 40663553 clock_gettime () 's por segundo
[*] Medición del tiempo MOVQ + CLFLUSH. Ejecutando 131072 iteraciones.
[*] Escribir datos
[*] Datos de entrada: min = 117 avg = 176 med = 167 max = 8172 ítems = 131072
[*] Rango de corte 212-inf
[] 127849 elementos por debajo del límite, 0 elementos por encima del límite, 3223 elementos distintos de cero
[*] Ejecutando FFT
[*] La frecuencia superior por encima de 2 kHz por debajo de 250 kHz tiene una magnitud de 7716
[+] Los picos de frecuencia superiores a 2 kHz están en:
127906Hz 7716
255813Hz 7947
383720Hz 7460
511626Hz 7141
Debo admitir que el código no es completamente estable. En caso de problemas, se recomienda desactivar Turbo Boost, la escala de frecuencia de la CPU y la optimización del rendimiento.
Conclusión
Hay dos conclusiones principales de este trabajo.
Vimos que los datos de bajo nivel son bastante difíciles de analizar y parecen bastante ruidosos. En lugar de evaluar a simple vista, siempre puedes usar la buena y antigua FFT. En la preparación de los datos, es necesario, en cierto sentido, hacer ilusiones.
Lo más importante es que hemos demostrado que a menudo es posible medir el comportamiento sutil del hardware desde un proceso simple en el espacio del usuario. Este tipo de pensamiento condujo al descubrimiento de la
vulnerabilidad original de Rowhammer , se implementó en los ataques Meltdown / Spectre y se mostró nuevamente en la reciente
reencarnación de Rowhammer para la memoria ECC .
Queda mucho más allá del alcance de este artículo. Apenas tocamos el funcionamiento interno del subsistema de memoria. Para leer más, recomiendo:
Finalmente, aquí hay una buena descripción de la antigua memoria de ferrita: