Nueva evidencia demuestra la existencia de dos tipos de curvas infinitas

El trabajo de Alexander Smith sobre la hipótesis de Goldfeld reveló las propiedades fundamentales de las curvas elípticas.

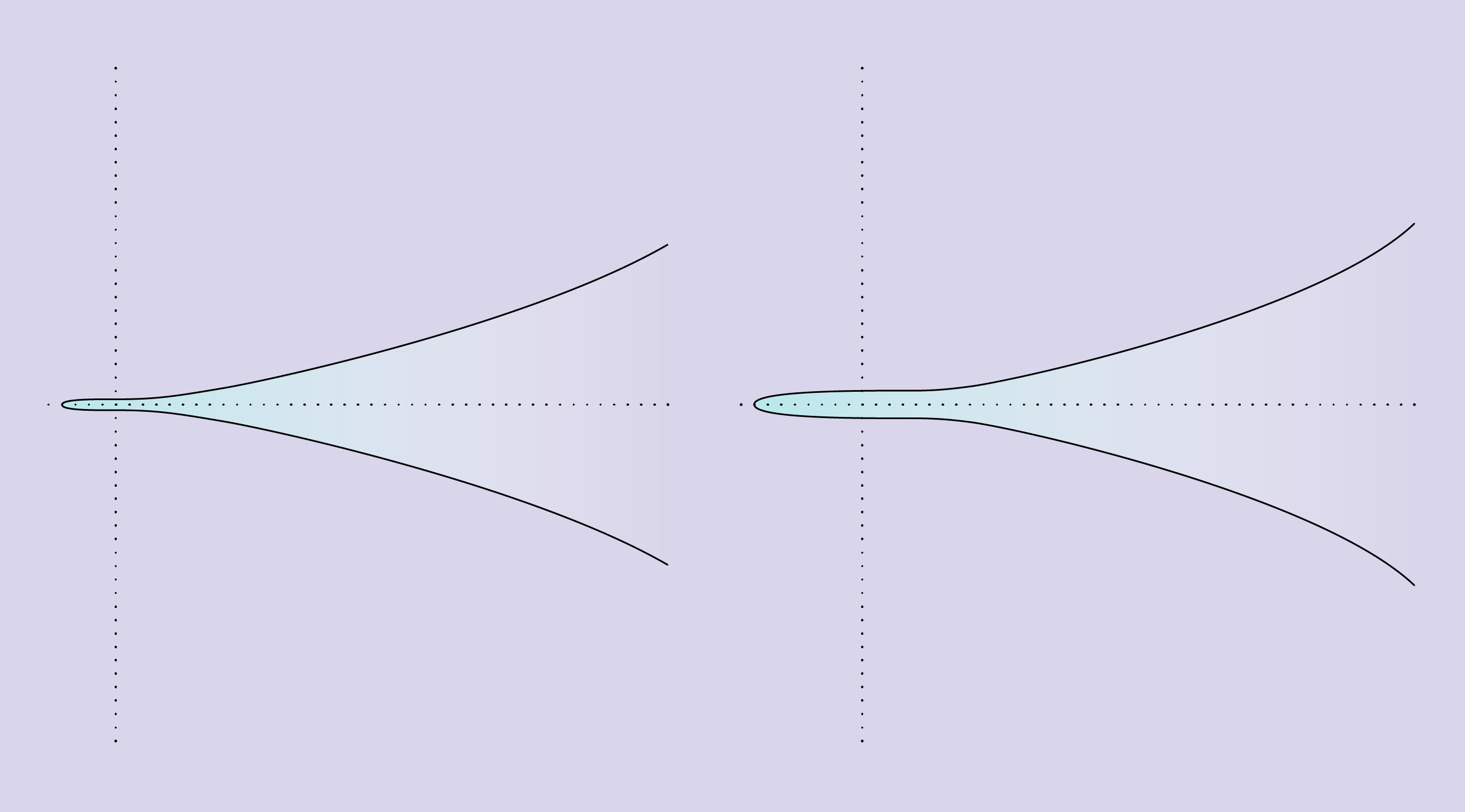Dos curvas elípticas demuestran la rareza del concepto de rango. La curva de la izquierda se describe mediante la ecuación y ² = x ³ + 1, pasa solo por cinco puntos racionales y tiene rango 0. La curva de la derecha se describe por la ecuación y ² = x ³ + 8, pasa por un número infinito de puntos racionales y tiene rango 1.

Puede haber muchas variantes de curvas elípticas, pero solo hay dos de sus variedades reales. Este es el resultado de la nueva evidencia recibida por un estudiante graduado de la Universidad de Harvard.

Las curvas elípticas parecen exóticas, pero estos son objetos geométricos poco notables, no más complicados que las líneas rectas, parábolas o elipses. En su trabajo publicado en línea el año pasado, Alexadr Smith demostró la hipótesis de hace cuarenta años sobre la característica fundamental de las curvas elípticas de rango. Smith demostró que de una familia dada de curvas que tiene una característica, la mitad tiene un rango de 0 y la otra mitad tiene un rango de 1.

Este resultado establece una característica de apoyo de los objetos que han ocupado a los matemáticos durante muchos siglos, cuya importancia ha crecido especialmente en las últimas décadas.

“Hemos estado pensando en esto por más de 1000 años, y ahora tenemos una comprensión probabilística de las curvas elípticas. Esto es extremadamente importante ”, dijo Shaw-U Zhang , matemático de la Universidad de Princeton que le dio a Smith recomendaciones sobre su trabajo cuando aún era estudiante en Princeton.

Las curvas elípticas son ecuaciones con variables elevadas a la tercera potencia, por ejemplo, y ² = x ³ + 1. Han aparecido en muchas pruebas matemáticas significativas en las últimas décadas, incluida la prueba más importante del Gran Teorema de Fermat de 1994. Parte de su importancia radica en el hecho de que pertenecen al tipo más complejo de ecuaciones polinómicas, sobre las cuales los matemáticos tienen algún tipo de ideas sistémicas.

"Las curvas elípticas son un caso interesante", dijo Dorian Goldfeld , matemático de la Universidad de Columbia, quien propuso en 1979 una hipótesis que obtuvo su nombre.

La hipótesis de Goldfeld hace predicciones sobre el rango de las curvas elípticas. Como ya hemos descrito en un artículo reciente, " ¿Qué evidencia puede convencer a los matemáticos si no hay una prueba rigurosa? " El rango es una medida de la complejidad de un conjunto de soluciones racionales de una curva (soluciones que se pueden representar como fracciones). Y aunque no hay una restricción comprobada en el rango de la curva, hasta ahora se considera que el 28 más alto es el rango más alto, la hipótesis de Goldfeld predice que, en promedio, la mitad de las curvas elípticas tienen un rango de 0, y la otra mitad tiene 1.

Puede que no le parezca claro cómo pueden existir curvas elípticas con un rango de más de 1 si la mitad de las curvas elípticas tienen un rango de 0 y la otra mitad tiene 1. Si tiene una caja de pelotas de ping-pong, y si sabe que exactamente la mitad de son negros y la mitad son blancos, entonces no puede haber rojos.

Aún más confuso es el hecho de que las curvas elípticas con un rango de 2 o superior existen no solo unas pocas, sino un número infinito. El resultado aparentemente absurdo es el resultado de estadísticas astutas que trabajan con infinitos. A pesar de que hay muchas curvas de rango 2 y superiores, hay tantas curvas con los rangos 0 y 1 que las curvas con rangos 2 y superiores no son estadísticamente significativas. Si coloca todas las curvas en una caja y las saca de allí al azar, entonces las posibilidades de sacar una curva con un rango de más de 1 son oficialmente iguales a cero.

¿Qué significa que el rango de la curva es 0? Dichas curvas tienen un número finito de puntos racionales, y no más de 16, como probó Barry Mazur en la década de 1970.


Dorian Goldfeld

Hay razones para creer que una gran cantidad de curvas elípticas tendrá un rango de 0. Si imagina cómo una curva corre a lo largo de un plano, se verá que la mayoría de los puntos a través de los cuales pasa no serán racionales. Estos puntos no pueden expresarse como fracciones, incluso si son arbitrariamente complejos. Las posibilidades de que una curva aleatoria se cruce con muchos puntos racionales, un conjunto infinito, son pequeñas.

"Lo tomo de esta manera: si tomas una curva elíptica aleatoria, entonces tendrá razones para tener un rango de 0. No quiere tener puntos racionales", dijo Smith.

La prevalencia de las curvas de rango 1 se explica de manera similar. Las curvas de rango 1 tienen infinitos puntos racionales, pero todos están muy bien alineados, por lo que pueden conectarse entre sí en un proceso bastante simple.

Para las curvas de rango 2 y superiores, los conjuntos de puntos racionales son más complicados. Contienen varios subconjuntos infinitos de puntos racionales que no están conectados entre sí.

“¿Cuáles son las posibilidades de la aparición de dos puntos independientes? - dijo Goldfeld. "Muy bajo". Mi hipótesis dice que esto debería suceder raramente ".

Cuando Goldfeld presentó su hipótesis por primera vez, la mayoría de los matemáticos la consideraron incorrecta. Señalaron los resultados de los experimentos computacionales, de los cuales se dedujo que las curvas con un rango de 2 o más alto ocurren con mucha más frecuencia que en el 0% de los casos.

Goldfeld respondió que simplemente toman el rango demasiado pequeño. Señaló que si estudia solo los primeros 10 enteros, puede obtener una estimación extremadamente inexacta de que el 40% de los números son primos. Del mismo modo, estos experimentos computacionales se han extrapolado de pequeños subconjuntos de curvas elípticas a familias de curvas infinitamente grandes.

“¡Dije mira los números primos! Esa fue mi respuesta. Necesitamos escalar mucho más alto, porque al principio puede aparecer mucha diversión ”, dijo Goldfeld.

La hipótesis de Goldfeld no se aplica a todas las curvas elípticas. Describe una familia especial de curvas elípticas, giros cuadráticos. Ejemplo: curva elíptica cy ² = x ³ - x, donde c es una constante. Al cambiar el valor de c, está doblando una curva elíptica. La hipótesis de Goldfeld se refiere a toda la variedad infinita de curvas que se pueden obtener cambiando el valor de c.

Alexander Smith testificó que Goldfeld tenía razón. En un nuevo artículo, demuestra que el 100% de las curvas elípticas (de un tipo especial) tienen un rango de 0 o 1. También demostró que estas curvas se dividen en partes iguales entre los dos rangos, aunque hay una trampa. Su prueba de la división 50–50 se basa en la validez de la hipótesis Birch - Swinnerton-Dyer (BJD). La hipótesis BSD es uno de los problemas abiertos más famosos en matemáticas. Los matemáticos aún no se han acercado a su prueba, pero en general lo consideran cierto.

Incluso con esa advertencia, el resultado de Smith se considera significativo. Los matemáticos dicen que él muestra una manera de probar completamente la hipótesis de Goldfeld sin jugar con la desalentadora hipótesis de BSD. Este método ofrece una nueva comprensión de la naturaleza de las curvas elípticas.

"El trabajo de Alex Smith es extremadamente interesante, y creo que aún debe estudiarse y recibir lo que merece", dijo Melanie Wood , matemática de la Universidad de Wisconsin. "El hecho de que esto se pueda probar es muy importante y revolucionario".