Una implementación práctica del generador de conmutación utilizando Verilog HDL

Resumen

Los registros de desplazamiento de retroalimentación lineal son una excelente herramienta para implementar un generador de bits pseudoaleatorio en hardware; inhiben una estructura electrónica simple y eficiente. Además, son capaces de producir secuencias de salida con períodos largos y buenas propiedades estadísticas. Sin embargo, los LFSR estándar no son criptográficamente seguros, ya que la secuencia de salida se puede predecir de manera única dado un pequeño número de bits de flujo de clave utilizando el algoritmo Berlekamp-Massey. Se han propuesto varios métodos para destruir la linealidad inherente al diseño de LFSR. Estos métodos incluyen generadores de combinación no lineales, generadores de filtro no lineales y generadores controlados por reloj. Sin embargo, siguen siendo vulnerables a muchos ataques, como los ataques de canal lateral y los ataques algebraicos. En 2015, se propuso un nuevo generador controlado con reloj, llamado generador de conmutación. Se ha demostrado que este nuevo generador es resistente a ataques algebraicos y ataques de canal lateral, al tiempo que conserva los requisitos de eficiencia y seguridad. En este proyecto, presentamos un diseño del generador de conmutación utilizando Verilog HDL.

Introducción y antecedentes históricos

La historia de la generación de números pseudoaleatorios en hardware está fuertemente vinculada al desarrollo de cifrados de flujo. Los cifrados de flujo son cifrados que cifran caracteres de texto sin formato individualmente (generalmente bit a bit), en contraste con los cifrados de bloque, que cifran texto sin formato en bloque grande (64 bits o más). Muchas arquitecturas de cifrado de flujo requieren un generador de flujo de clave, que es un generador de bits pseudoaleatorio cuya semilla es la clave de cifrado. Para cada bit de texto sin formato, el bit de texto de cifrado correspondiente se calcula como alguna función reversible (generalmente xor gate) del bit de texto sin formato y el bit de secuencia de clave correspondiente. Por lo tanto, diseñar generadores de flujo de clave seguros y eficientes es esencial para la operación de cifrado de flujo.


Una herramienta útil para construir generadores de flujo clave son los registros de desplazamiento de retroalimentación lineal. Se pueden construir fácilmente mediante componentes electrónicos elementales y se pueden programar simplemente en dispositivos lógicos programables. Además, debido a su estructura simple, los LFSR se pueden modelar y analizar matemáticamente, lo que ha llevado a un vasto cuerpo de conocimiento y resultados con respecto a ellos. La secuencia de salida de un LFSR correctamente construido tiene una longitud exponencial y buenas propiedades estadísticas, como una gran complejidad lineal.


A pesar de las buenas propiedades estadísticas del LFSR, no puede usarse como generador de flujo de claves en su forma estándar debido a su naturaleza lineal. Si un atacante lograra saber $$$2L$ bits de secuencia de clave consecutivos, entonces la secuencia de salida se puede predecir de manera única y eficiente utilizando el algoritmo Berlekamp-Massey, donde $$$L$ es el número de registros Se han propuesto muchas formas diferentes de destruir la linealidad inherente a la secuencia de salida LFSR:

• Utilizando múltiples LFSR y una función de combinación no lineal de sus salidas (generadores de combinación no lineal).
• Generando la secuencia de salida como alguna función no lineal del estado LFSR (generadores de filtro no lineales).
• Reloj irregular de LFSR (generadores controlados por reloj).

Aún así, todos estos diseños permanecieron vulnerables a ataques como los ataques algebraicos y de canal lateral. Después del año 2000, esto ya no era un problema crítico, ya que el cifrado en bloque Rijndael fue propuesto y elegido como el Estándar de cifrado avanzado (AES). AES era capaz de operar en modo de cifrado de flujo y cumplir con todos los estándares industriales para un cifrado de flujo. Además, con el aumento de los poderes computacionales, AES podría implementarse en varias plataformas. Esto ha llevado a una disminución significativa en las aplicaciones de cifrado de flujo.


Adi Shamir presentó una conferencia invitada en State of the Art en Stream Ciphers 2004 y Asiacrypt 2004 titulada "Stream Ciphers: Dead or Alive?". En su presentación, sugirió que los cifrados de flujo pueden sobrevivir en las siguientes aplicaciones:

• Aplicaciones orientadas al software con velocidades excepcionalmente altas (por ejemplo, enrutadores).
• Aplicaciones orientadas al hardware con una huella excepcionalmente pequeña (por ejemplo, tarjetas inteligentes).

Una de las últimas propuestas para generadores de flujo clave es el generador de conmutación. Se afirma que es resistente a los ataques algebraicos y de canales laterales, a la vez que conserva la eficiencia y las velocidades de operación.


En este proyecto, presentaremos un diseño del generador de conmutación en hardware, utilizando Verilog HDL. Primero, presentamos las dos formas comunes de LFSR, Fibonacci LFSR y Galois LFSR. A continuación, presentamos una presentación matemática de LFSR. Luego presentaremos el generador de conmutación tal como lo introdujo. Finalmente, presentamos nuestro diseño Verilog del generador de conmutación.

Registros de desplazamiento de retroalimentación lineal

Los registros de desplazamiento de retroalimentación lineal son circuitos que consisten en una lista lineal de registros (también llamados elementos de retardo) y un conjunto predefinido de conexión entre ellos. Una señal de reloj global (única) controla el flujo de datos dentro del LFSR. Los dos tipos de LFSR más utilizados son los LFSR de Fibonacci y los LFSR de Galois; diferiendo solo en forma de conexiones. Como veremos más adelante en la sección del modelo matemático, existen muchas similitudes entre las arquitecturas de Fibonacci y Galois, prefiriendo una sobre la otra es específica de la aplicación.


A lo largo de este artículo, asumimos un contador de tiempo global hipotético que comienza en $$$0$ y aumentando por $$$1$ después de cada borde positivo del ciclo global del reloj.

Registros

Un registro es un elemento lógico capaz de almacenar un bit de datos, llamado estado. Tiene dos líneas de entrada: una línea de datos de un bit y una línea de señal de reloj. Tiene una salida de un bit que siempre es igual al estado interno. En cada borde positivo de la entrada del reloj, la entrada de datos se asigna al estado; de lo contrario, el estado permanece sin cambios. Denotemos el estado de un registro $$$S$ a tiempo $$$t$ como $$$\ mathop S \ nolimits ^ t$ .

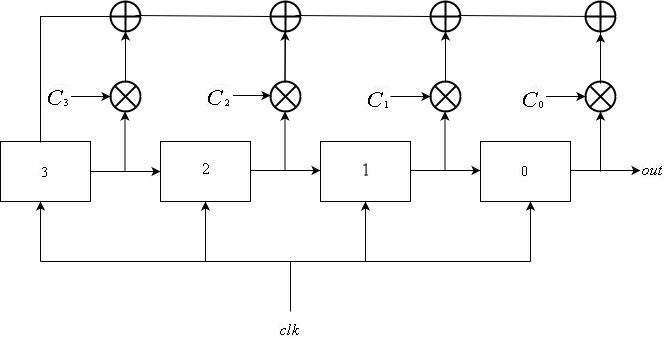
Fibonacci lfsrs

Un LFSR de Fibonacci consta de $$$L$ registros enumerados desde $$$0$ a $$$L-1$ , todos conectados a la misma señal de reloj. La entrada de registro $$$i$ es la salida del registro $$$i + 1$ para $$$0 \ le i \ le L-2$ . La entrada de retroalimentación para el registro $$$L-1$ es la suma xor de salidas de algún subconjunto de registros. La actualización del registro se puede describir matemáticamente de la siguiente manera:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {if} \ \} 0 \ le i \ le L-2 \\ \ mathop \ bigoplus \ limits_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ right.$$

donde $$$C_j = 1$ si se registra $$$j$ está incluido en los comentarios y $$$0$ de lo contrario

La secuencia de salida se obtiene del registro $$$0$ . Es decir, la secuencia de salida es $$$\ mathop {\ left \ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

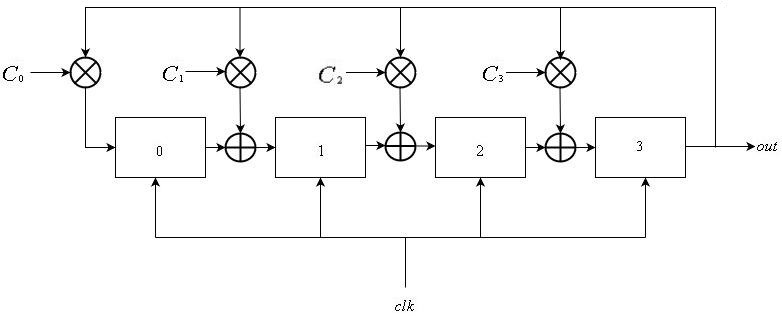
Galois LFSRs

Los LFSR de Galois también consisten en una lista lineal de $$$L$ registros enumerados desde $$$0$ a $$$L-1$ , todos compartiendo la señal de reloj global. La entrada de registro $$$i$ es la salida del registro $$$i-1$ para $$$1 \ le i \ le L-1$ . Para algunos subconjuntos de registros, su entrada se sincroniza con la salida del registro $$$L-1$ . Esto se puede expresar como:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ \ if \ \}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \}} i = 0 \ end {array} \ right.$$

donde $$$C_i = 1$ si la entrada de registro $$$i$ se graba con salida de registro $$$L-1$ .


De manera similar a la de los LFSR de Fibonacci, la secuencia de salida se define como $$$\ mathop {\ left \ {{\ mathop S \ nolimits_ {L-1} ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

Comparación entre los diseños de Fibonacci y Galois

Hay una correspondencia directa entre Fibonacci y Galois LFSR en el sentido matemático, como veremos en la siguiente sección. Sin embargo, hay dos ventajas notables de usar el diseño de Galois:

• En la implementación de software, no requiere un $$$L$ comprobación de paridad de bits, que agrega un factor logarítmico de complejidad.
• En la implementación de hardware, solo requiere puertas xor de dos entradas, cuyo retraso de propagación es significativamente menor que el de las puertas xor de entradas múltiples utilizadas en el diseño de Fibonacci.

En nuestro proyecto, consideramos la formulación matricial de la LFSR, por lo que ambas arquitecturas son intercambiables.

Modelo matemático de LFSR

En las siguientes secciones, a menos que se indique lo contrario, asumimos que todos los cálculos se realizan en el campo de Galois $$$Gf \ izquierda (2 \ derecha)$ . Es decir, todas las operaciones son módulo calculado $$$2$ . Otra implementación de esta convención es que toda multiplicación es una puerta lógica, y toda suma es una puerta xor.


Considere los estados de todos $$$L$ registros de un LFSR en algún momento $$$t$ ; esto puede representarse como un vector de $$${\ left \ {{0,1} \ right \} ^ L}$ :

$$

$${S ^ t} = \ left ({\ mathop S \ nolimits_0 ^ t; \ mathop S \ nolimits_1 ^ t; \ ldots; \ mathop S \ nolimits_ {L-1} ^ t} \ right)$$

Denotamos este vector como el estado de la LFSR. Tenga en cuenta que hay a lo sumo $$${2 ^ L}$ posibles estados para un $$$L$ registrarse LFSR. También tenga en cuenta que si un LFSR alcanzara el estado todo cero, no podría alcanzar ningún otro estado. Por eso decimos que hay $$$2 ^ L-1$ no trivial de un LFSR.


Considere la siguiente transformación lineal:

$$

$$F = \ left ({\ begin {array} {* {20} {c}} 0 & 1 & \ cdots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \\ {\ mathop C \ nolimits_0} & {\ mathop C \ nolimits_1} & \ cdots & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

Dado que $$$\ mathop S \ nolimits ^ t$ es el estado de un LFSR de Fibonacci, se puede observar que

$$

$$F \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Si $$$\ mathop S \ nolimits ^ t$ era un estado de un Galois LFSR, entonces considere la transformación $$$G$ :

$$

$$G = \ left ({\ begin {array} {* {20} {c}} 0 & \ cdots & 0 & {\ mathop C \ nolimits_0} \\ 1 & \ cdots & 0 & {\ mathop C \ nolimits_1} \\ \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 1 & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

En este caso, tenemos

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Las representaciones matriciales de LFSR pueden ser flexibles cuando se trata de actualizaciones repetidas, ya que pueden interpretarse como un producto matricial simple. Se puede observar que $$$F = {G ^ T}$ . Este hecho indica las muchas similitudes entre los diseños de Fibonacci y Galois si fueran vistos como transformaciones lineales de $$${\ left \ {{0,1} \ right \} ^ N}$ a $$${\ left \ {{0,1} \ right \} ^ N}$ .


Multiplicar el vector de estado de algunos LFSR por una matriz (de los tipos Fiboancci o Galois) se conoce como cronometrar o actualizar el LFSR.

El generador de conmutación

El Switching Generator es un generador controlado por reloj propuesto en 2015. Se ha demostrado que tiene resistencia a los ataques algebraicos y de canales laterales. En esta sección, presentaremos el diseño del generador de conmutación, según lo especificado por sus inventores.

Estructura básica

El generador de conmutación consta de dos LFSR: un control LFSR $$$A$ de longitud $$$N$ y un LFSR de datos $$$B$ de longitud $$$M$ . El control LFSR se actualiza como se describió anteriormente. Sin embargo, los datos LFSR se actualizan utilizando una de las dos posibles matrices, $$$\ mathop M \ nolimits_1 ^ i$ o $$$\ mathop M \ nolimits_2 ^ j$ donde $$${M_1}, {M_2}$ son matrices compañeras de algunos polinomios primitivos. La elección de una matriz sobre la otra está determinada por la salida de señal del control LFSR. Este proceso se puede describir de la siguiente manera:

$$

$$\ mathop B \ nolimits ^ t = \ left \ {\ begin {array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \ right.$$

La salida del generador de conmutación es la salida de LFSR $$$B$ . Tenga en cuenta que asumimos que $$$A$ es un Galois LFSR. También puede ser un LFSR de Fibonacci.


Enteros $$$i, j$ Se llaman los índices de cambio.

La semilla

Recuerde que un LFSR puede iterar como máximo $$${2 ^ L} -1$ estados no triviales antes de volver a visitar estados anteriores. Desde matrices $$${M_1}, {M_2}$ son matrices de transformación de LFSR, podemos deducir que los enteros $$$i, j$ puede ser a lo sumo $$$2 ^ M-1$ antes de que las matrices comiencen a repetirse.


La semilla para el generador de conmutación es $$$N + 3M$ bits, que representan los estados iniciales de los LFSR $$$A$ y $$$B$ y los poderes enteros $$$i, j$ . Tenga en cuenta que las matrices $$${M_1}, {M_2}$ se arreglan a lo largo de la implementación y no se incluyen en la semilla.

Diseño Verilog

En esta sección, presentaremos nuestro diseño del generador de conmutación utilizando Verilog HDL. Presentaremos cada diseño de módulo de manera ascendente. Al final, presentamos el módulo generador de conmutación.


En nuestro diseño, tratamos de mantener los componentes síncronos al mínimo. Los únicos componentes controlados por reloj son los LFSR $$$A, B$ .


Las operaciones matriciales y vectoriales se pueden implementar en varios métodos diferentes, que varían en el consumo de unidades lógicas, unidades de memoria y complejidad de procedimiento. En nuestro diseño, eliminamos la necesidad de bloques de procedimiento y usamos elementos lógicos al máximo.


Todas las matrices en los siguientes módulos están indexadas a partir de $$$0$ De izquierda a derecha, y luego de arriba a abajo.


También tenga en cuenta que todos los módulos tienen tamaños parametrizados; Esto es para fines de depuración. En una implementación real, todos los tamaños son fijos.

Multiplexor

Este es un módulo que implementa un 2 a 1 $$$N$ multiplexor de bits. El módulo tiene dos $$$N$ líneas de entrada de un bit, una línea de selección de 1 bit y $$$N$ línea de salida de bits. Si la entrada del selector es $$$0$ entonces la salida se establece en la primera línea de entrada, de lo contrario se establece en la segunda.


Módulo multiplexor

Transformación del vector

Este módulo implementa una transformación lineal en un vector. Acepta como entrada un $$$N \ veces N$ matriz de transformación y una $$$N$ -bit vector. Produce el producto matriz-vector de su entrada.


Cada bit en el vector de salida es el resultado de un $$$N$ -bit xor gate, tomando como entrada el resultado de la $$$N$ -bit bit a bit y del vector de entrada y la fila de matriz correspondiente. Es decir, cada bit de salida está conectado a la entrada y no se necesitan bloques de procedimiento.


Exactamente $$$N ^ 2$ se utilizan dos entradas y puertas, junto con $$$N$$$$N$ -Puertas de entrada xor.


Módulo de transformación de vectores

Identidad

Este módulo no acepta entradas. Su $$$N \ veces N$ -bit de salida se inicializa a la $$$N$ matriz de identidad. Dicho módulo se declara por conveniencia, para que no tengamos que inicializar un vector de registro global para cada tamaño diferente.


Módulo de matriz de identidad

Transponer

Este módulo acepta un $$$N \ veces N$ matriz y salida su transposición. No se utilizan elementos lógicos ni de memoria en este módulo, su salida es simplemente una permutación de su entrada
.

Módulo de transposición de matrices

Multiplicación matricial

Este es un módulo que implementa la multiplicación matriz-matriz. Acepta dos $$$N \ veces N$ matrices como entrada y salidas de su producto matriz-matriz.


Este módulo contiene una instancia del módulo de transposición de matriz. Esto hace posible asignar índices consecutivos a columnas en la segunda matriz de entrada. Cada entrada en la matriz de salida se asigna a la salida de un $$$N$ -input xor gate, cuya entrada es a nivel de bit y de la fila correspondiente de la primera matriz y columna de la segunda.


Exactamente $$$N ^ 3$ dos entradas y puertas y $$$N ^ 2$$$$N$ -input xor se utilizan en esta implementación.


Módulo de multiplicación de matrices

Matriz de exponenciación

Este módulo eleva una matriz a una potencia entera. Acepta como entrada un $$$N \ veces N$ matriz y una $$$K$ -bit entero. Su salida es la matriz elevada a la potencia entera especificada.


Módulo de exponenciación matricial

Unidad de control

Este módulo implementa el $$$N$ -bit control LFSR. Es uno de los dos módulos controlados por reloj en nuestro diseño.


Incluye una estática $$$N \ veces N$ Matriz de transformación LFSR y una variable $$$N$ -bit estado. Su entrada incluye un reloj, un $$$N$ -bit restablecimiento de estado y una señal de reinicio. Su salida es un solo bit, que es el último bit del LFSR.


Después de cada borde positivo de la señal de reloj, el estado se actualiza de acuerdo con la matriz de transformación utilizando un módulo de multiplicación de matriz-vector. El restablecimiento de estado se asigna al estado interno después de cada borde positivo de la señal de restablecimiento.





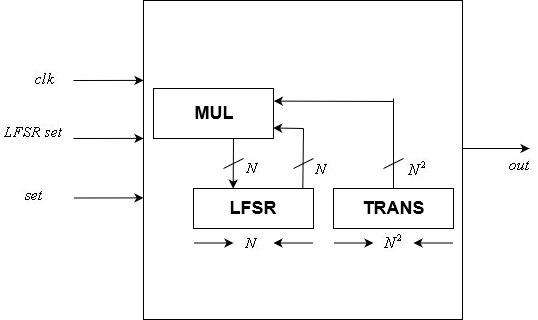Módulo de unidad de control

Unidad de datos

El $$$N$ Los datos LFSR se implementan utilizando este módulo. Al igual que el módulo de la unidad de control, es controlado por reloj


El módulo incluye dos $$$N \ veces N$ matrices de transformación y una $$$N$ -bit estado LFSR. Acepta como entrada una señal de reloj, una señal de control, un $$$N$ -bit restablecimiento de estado LFSR, dos $$$N \ veces N$ la transformación de la matriz se restablece y una señal de reinicio. Tiene una salida de un bit, el último bit del LFSR interno.


Tenga en cuenta que, dado que la semilla se puede cambiar, las matrices de transformación también se pueden cambiar, a diferencia de la unidad de control cuya matriz de transformación está fija.




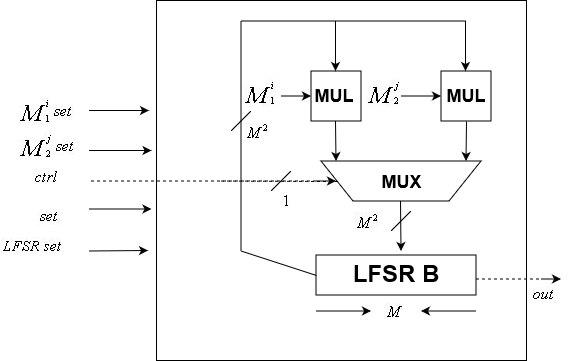\ Unidad de datos

El generador de conmutación

Este es el módulo principal de nuestro diseño. Está parametrizado por enteros $$$N, M$ , que son los tamaños de las unidades de control y datos, respectivamente.


La entrada a este módulo es una señal de reloj, un $$$N + 3M$ -bit semilla, y una señal establecida. La semilla es simplemente una concatenación del restablecimiento de LFSR de control, el restablecimiento de LFSR de datos y los enteros $$$i, j$ Su salida es de un bit, el bit seudoaleatorio generado por el generador de conmutación.


Este módulo incluye dos $$$M \ veces M$ matrices $$$\ mathop M \ nolimits_1, \ mathop M \ nolimits_2$ . Estas matrices se arreglan a lo largo de la implementación.


Se utilizan dos instancias de módulos de exponenciación matricial para calcular las matrices de entrada para la unidad de datos, donde su entrada son las matrices de transformación fija y los enteros $$$i, j$ , extraído de la semilla.


El módulo generador de conmutación

Conclusiones y recomendaciones.

En este proyecto, hemos presentado un diseño del generador de conmutación utilizando Verilog HDL. Este diseño está enfocado completamente en hardware y elimina el uso de bloques de procedimiento. Tal enfoque permite el máximo rendimiento a costa de los elementos lógicos y de memoria. Para algunas aplicaciones con restricciones de elementos lógicos y de memoria, puede ser beneficioso sacrificar el rendimiento y aumentar el uso de bloques de procedimiento para reducir el uso de elementos electrónicos.


Un inconveniente del proyecto es que tiene la responsabilidad de elegir buenos índices de cambio para el usuario. Un posible avance es agregar un componente de hardware para verificar la validez del índice de conmutación utilizado. Esto requiere una implementación de hardware de algoritmos complejos, como encontrar el polinomio de características de una matriz dada y verificar su primitividad.


Un posible avance es agregar un verdadero generador de números aleatorios para verificar los índices de conmutación aleatoria y generar un par válido una vez que se encuentre. Se puede demostrar que este proceso se detiene después de un corto tiempo con alta probabilidad.

Referencias

1. Katz, Jonathan y col. Manual de criptografía aplicada. Prensa CRC, 1996.
2. Choi, Jun y col. "El generador de conmutación: nuevo generador controlado por reloj con resistencia contra los ataques algebraicos y de canal lateral". Entropía 17.6 (2015): 3692-3709.
3. Shamir, Adi. "Cifrados de flujo: ¿vivo o muerto?" ASIACRIPTO 2004
4. LFSR para los no iniciados