Un poco de teoría que sé sobre el sonido: el sonido es:
onda, oscilaciones, oscilaciones amortiguadas, la onda se puede describir desde el punto de vista de la física, la onda se puede describir desde el punto de vista de las matemáticas.
Descargue y pruebe el programa
Como estamos modelando en una computadora, nuestra onda se describe usando una secuencia (serie de Fourier) de bytes (números de -128 a 127 y cero), es decir, una matriz de bytes.
La ecuación vibratoria se describe mejor con la función SIN.
De acuerdo, sería demasiado simple si solo ejecutáramos la función SIN a través de la matriz.
Por lo tanto, guiado por artículos sobre la descripción del dispositivo sintetizador Yamaha, escribí el siguiente algoritmo:
1. Usando la función SIN, se crea una onda principal o de modelado, aquí hay una fórmula que puede ser útil para otros desarrolladores:
for(int k = 0; k < SoundLabVisual.player.data.length;k++){ double sinusoid = amplitude1 * Math.sin(2 * (3.14/1 ) * k * frequency1 + faza); }
Donde:
amplitud1 - amplitud
frecuencia1 - frecuencia de oscilación
faza - la fase inicial de las oscilaciones
2. Usando la segunda función SIN, se crea una onda principal, con la amplitud de los valores de la primera onda:
Captura de pantalla del programa
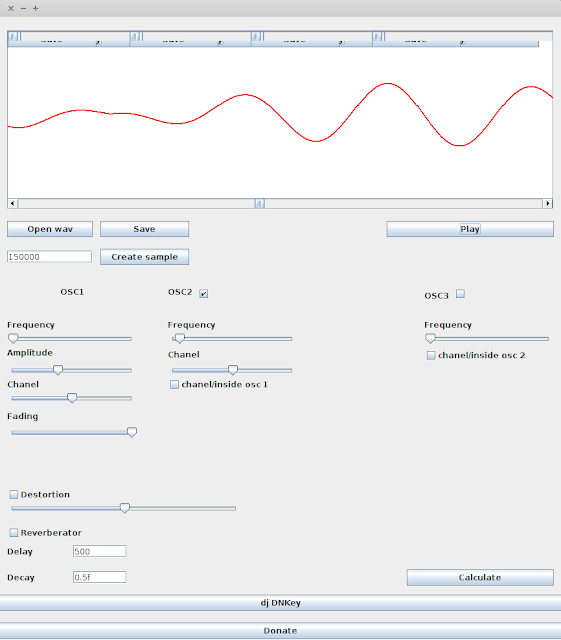
Cargué los sonidos de prueba en el programa lmms.
 Escuchar mp3
Escuchar mp3Se implementará otro algoritmo que funcionará en los canales, si es posible, escribiré sobre eso en el segundo artículo.
Actualización:
Según los comentarios de los comentaristas, los algoritmos ahora pueden multiplicarse por sí mismos y entre ellos.
if(jCheckBox8.isSelected()){ sinusoid = (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))) * (a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 ))); }else{ sinusoid = a1 + (sinusoid * Math.sin( (c1 * (double)k) * frequency2Double + d1 )); }
Actualización 2: el programa se ha actualizado, ahora la onda se puede mezclar con el sonido.