El artículo está escrito sobre el análisis y estudio de materiales de la competencia para la búsqueda de barcos en el mar.

Tratemos de entender cómo y qué busca la red y qué encuentra. Este artículo es simplemente el resultado de la curiosidad y el interés ocioso, nada de eso se encuentra en la práctica y para tareas prácticas no hay nada para copiar y pegar. Pero el resultado no es del todo esperado. Internet está lleno de descripciones del funcionamiento de las redes en las que los autores describen maravillosamente y con imágenes cómo las redes determinan las primitivas: ángulos, círculos, bigotes, colas, etc., luego se buscan segmentación / clasificación. Muchas competiciones se ganan usando pesos de otras redes grandes y anchas. Es interesante entender y ver cómo y qué primitivas construye una red.
Realizaremos un pequeño estudio y consideraremos las opciones: se presentan el razonamiento y el código del autor, puede verificar / complementar / cambiar todo usted mismo.
La competencia de búsqueda marina de kaggle ha finalizado recientemente. Airbus propuso analizar imágenes satelitales del mar con y sin barcos. En total, 192555 imágenes 768x768x3 - es 340 720 680 960 bytes si uint8 y cuatro veces más si float32 (por cierto float32 es más rápido que float64, menos acceso a memoria) y en 15606 imágenes necesita encontrar barcos. Como de costumbre, todos los lugares importantes fueron ocupados por personas involucradas en SAO (ods.ai), lo cual es natural y esperado, y espero que pronto podamos estudiar el tren de pensamiento y el código de ganadores y ganadores de premios.
Consideraremos un problema similar, pero lo simplificaremos significativamente: tome el mar np.random.sample () * 0.5, no necesitamos olas, viento, playas y otros patrones y caras ocultos. Hagamos que la imagen del mar sea realmente aleatoria en el rango RGB de 0.0 a 0.5. También pintaremos las embarcaciones del mismo color y para distinguirlas del mar, las colocaremos en el rango de 0.5 a 1.0, y todas tendrán la misma forma: elipses de diferentes tamaños y orientaciones.

Tome una versión muy común de la red (puede tomar su red favorita) y haremos todos los experimentos con ella.
A continuación, cambiaremos los parámetros de la imagen, crearemos interferencia y construiremos hipótesis, por lo que destacaremos las características principales por las cuales la red encuentra puntos suspensivos. Quizás el lector saque sus conclusiones y refute al autor.
Cargamos bibliotecas, determinamos los tamaños de una serie de imágenes.import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm_notebook, tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.callbacks import EarlyStopping, ModelCheckpoint, ReduceLROnPlateau from keras.models import load_model from keras.optimizers import Adam from keras.layers import Input, Conv2D, Conv2DTranspose, MaxPooling2D, concatenate, Dropout from keras.losses import binary_crossentropy import tensorflow as tf import keras as keras from keras import backend as K from tqdm import tqdm_notebook w_size = 256 train_num = 8192 train_x = np.zeros((train_num, w_size, w_size,3), dtype='float32') train_y = np.zeros((train_num, w_size, w_size,1), dtype='float32') img_l = np.random.sample((w_size, w_size, 3))*0.5 img_h = np.random.sample((w_size, w_size, 3))*0.5 + 0.5 radius_min = 10 radius_max = 30
determinar las funciones de pérdida y precisión def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
Utilizamos la métrica clásica en la segmentación de imágenes, hay muchos artículos, código con comentarios y texto sobre la métrica seleccionada, en el mismo kaggle hay muchas opciones con comentarios y explicaciones. Vamos a predecir la máscara del píxel: este es el "mar" o "bote" y evaluaremos la verdad o la falsedad de la predicción. Es decir Son posibles las siguientes cuatro opciones: predijimos correctamente que un píxel es un "mar", predijimos correctamente que un píxel es un "barco" o cometimos un error al predecir un "mar" o un "barco". Entonces, para todas las imágenes y todos los píxeles, estimamos el número de las cuatro opciones y calculamos el resultado; este será el resultado de la red. Y cuanto menos predicciones erróneas y más verdaderas, cuanto más preciso sea el resultado y mejor será la red.
Y para la investigación, tomemos la bien estudiada u-net, que es una excelente red para la segmentación de imágenes. La red es muy común en tales competiciones y hay muchas descripciones, sutilezas de aplicación, etc. Se eligió una variante del clásico U-net y, por supuesto, fue posible actualizarlo, agregar bloques residuales, etc. Pero "no puedes aceptar la inmensidad" y realizar todos los experimentos y pruebas a la vez. U-net realiza una operación muy simple con imágenes: reduce el tamaño de la imagen con algunas transformaciones paso a paso y luego intenta recuperar la máscara de la imagen comprimida. Es decir La dimensión de la imagen en nuestro caso se lleva a 32x32 y luego intentamos restaurar la máscara utilizando los datos de todas las compresiones anteriores.
En la imagen, el esquema U-net es del artículo original, pero lo rehicimos un poco, pero la esencia sigue siendo la misma: comprimimos la imagen → expandimos en una máscara.
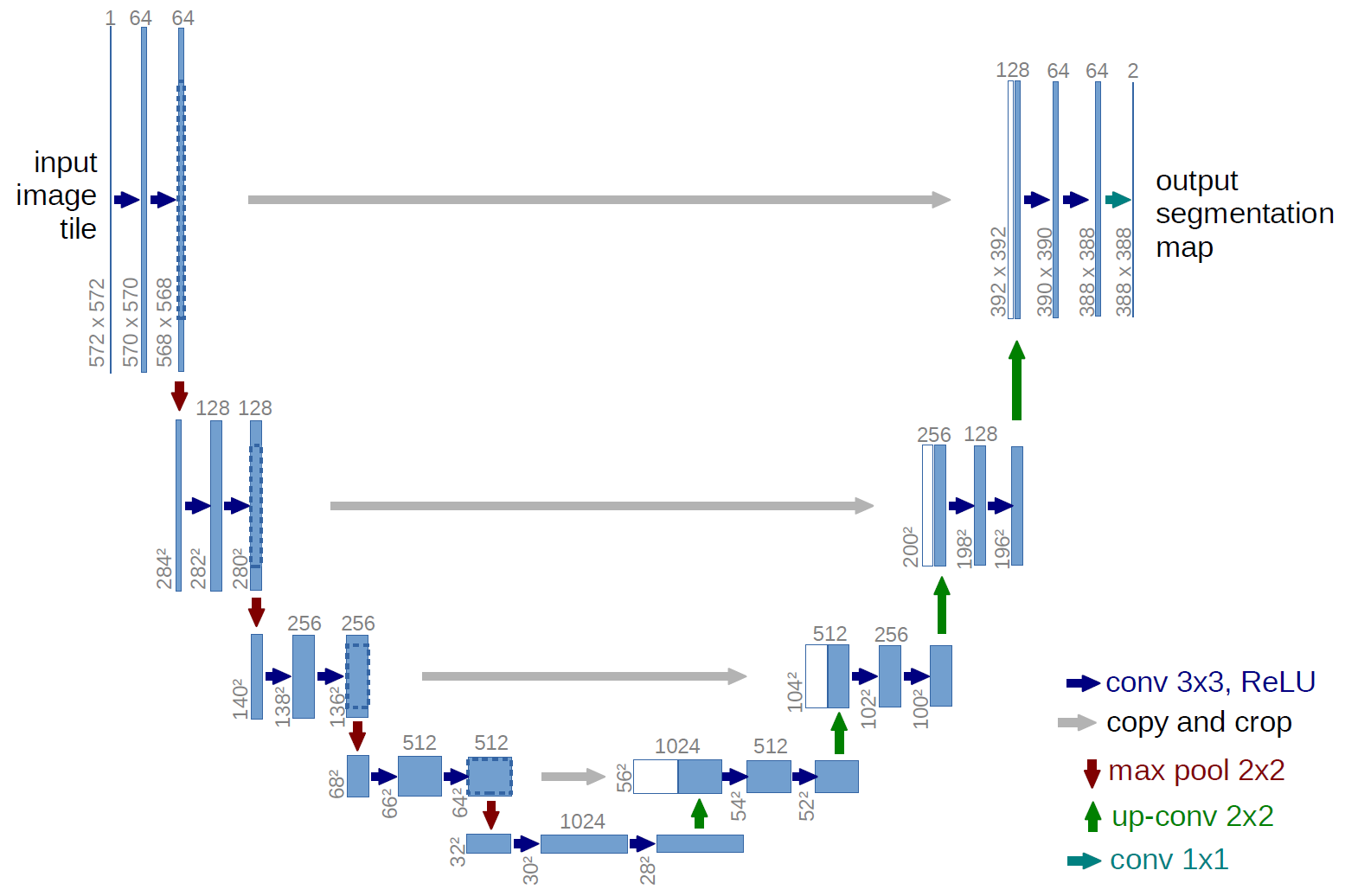
Solo U-net def build_model(input_layer, start_neurons): conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(input_layer) conv1 = Conv2D(start_neurons*1,(3,3),activation="relu", padding="same")(conv1) pool1 = MaxPooling2D((2, 2))(conv1) pool1 = Dropout(0.25)(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(pool1) conv2 = Conv2D(start_neurons*2,(3,3),activation="relu", padding="same")(conv2) pool2 = MaxPooling2D((2, 2))(conv2) pool2 = Dropout(0.5)(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(pool2) conv3 = Conv2D(start_neurons*4,(3,3),activation="relu", padding="same")(conv3) pool3 = MaxPooling2D((2, 2))(conv3) pool3 = Dropout(0.5)(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(pool3) conv4 = Conv2D(start_neurons*8,(3,3),activation="relu", padding="same")(conv4) pool4 = MaxPooling2D((2, 2))(conv4) pool4 = Dropout(0.5)(pool4)
Primer experimento Más fácil
La primera versión de nuestro experimento fue elegida para que la simplicidad sea muy simple: el mar es más claro, los barcos son más oscuros. Todo es muy simple y obvio, tenemos la hipótesis de que la red encontrará naves / elipses sin problemas y con precisión. La función next_pair genera un par de imagen / máscara, en la que se seleccionan al azar el lugar, el tamaño y el ángulo de rotación. Además, se realizarán todos los cambios a esta función: un cambio de color, forma, interferencia, etc. Pero ahora la opción más fácil, probamos la hipótesis de los barcos oscuros sobre un fondo claro.
def next_pair(): p = np.random.sample() - 0.5
Generamos todo el tren y vemos qué pasó. Parecen barcos en el mar y nada más. Todo es claramente visible, claro y comprensible. La ubicación es aleatoria y solo hay una elipse en cada imagen.
for k in range(train_num):
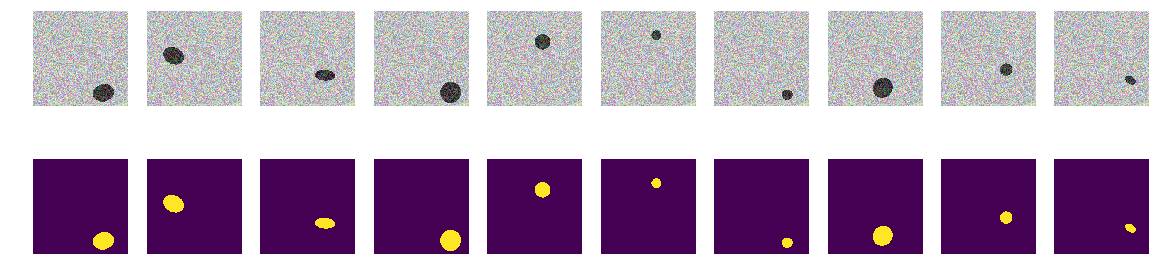
No hay duda de que la red aprenderá con éxito y encontrará puntos suspensivos. Pero probemos nuestra hipótesis de que la red está entrenada para encontrar elipses / naves y al mismo tiempo con alta precisión.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.save_weights('./keras.weights') while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.2272 - my_iou_metric: 0.7325 - val_loss: 0.0063 - val_my_iou_metric: 1.0000
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0090 - my_iou_metric: 1.0000 - val_loss: 0.0045 - val_my_iou_metric: 1.0000
La red encuentra con éxito elipses. Pero no está del todo comprobado que esté buscando elipses en la comprensión del hombre, como una región limitada por la ecuación de elipse y llena de contenido diferente del fondo, no hay certeza de que haya pesos de red similares a los coeficientes de la ecuación de elipse cuadrática. Y es obvio que el brillo de la elipse es menor que el brillo del fondo y no tiene secretos ni adivinanzas; suponemos que acabamos de verificar el código. Arreglemos la cara obvia, hagamos que el fondo y el color de la elipse sean aleatorios también.
Segunda opción
Ahora las mismas elipses están en el mismo mar, pero el color del mar y, en consecuencia, el barco se elige al azar. Si el mar es más oscuro, el barco será más claro y viceversa. Es decir Por el brillo del grupo de puntos es imposible determinar si están fuera de la elipse, es decir, el mar o estos son puntos dentro de la elipse. Nuevamente, probamos nuestra hipótesis de que la red encontrará elipses independientemente del color.
def next_pair(): p = np.random.sample() - 0.5
Ahora, por el píxel y sus alrededores, es imposible determinar el fondo o la elipse. También generamos imágenes y máscaras y miramos los primeros 10 en la pantalla.
construyendo máscaras for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
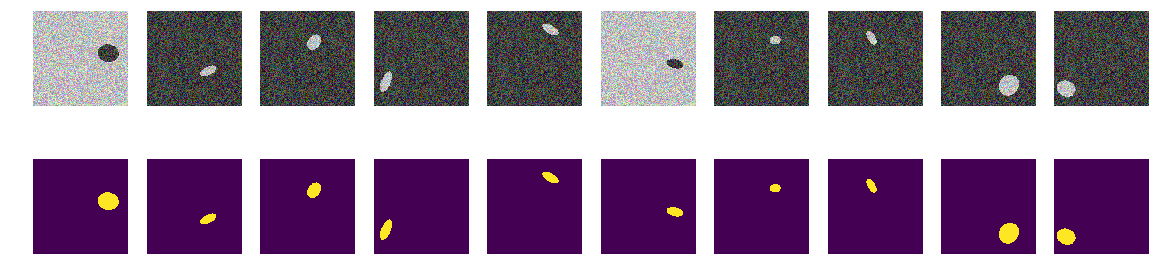
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.4652 - my_iou_metric: 0.5071 - val_loss: 0.0439 - val_my_iou_metric: 0.9005
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.1418 - my_iou_metric: 0.8378 - val_loss: 0.0377 - val_my_iou_metric: 0.9206La red hace frente fácilmente y encuentra todas las elipses. Pero aquí, hay una falla en la implementación, y todo es obvio: la menor de las dos áreas en la imagen es una elipse, otro fondo. Quizás esta sea una hipótesis falsa, pero aún así corríjala, agregue otro polígono a la imagen del mismo color que la elipse.
Tercera opción
En cada imagen, elegimos al azar el color del mar entre las dos opciones y agregamos una elipse y un rectángulo, los cuales son diferentes del color del mar. Resulta el mismo "mar", también un "bote" pintado, pero en la misma imagen agregamos un rectángulo del mismo color que el "bote" y también con un tamaño seleccionado al azar. Ahora nuestra suposición es más complicada, en la imagen hay dos objetos idénticamente coloreados, pero tenemos la hipótesis de que la red aún aprenderá a elegir el objeto correcto.
programa para dibujar elipses y rectángulos Como antes, calculamos imágenes y máscaras y observamos los primeros 10 pares.
la construcción de imágenes de máscaras elipses y rectángulos for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 57s 8ms/step - loss: 0.7557 - my_iou_metric: 0.0937 - val_loss: 0.2510 - val_my_iou_metric: 0.4580
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 55s 7ms/step - loss: 0.0719 - my_iou_metric: 0.8507 - val_loss: 0.0183 - val_my_iou_metric: 0.9812Los rectángulos de la red no pueden confundirse, y nuestra hipótesis se confirma. A juzgar por los ejemplos y las discusiones, todos en la competencia de Airbus tenían barcos individuales, y varios barcos estaban cerca con bastante precisión. La elipse del rectángulo, es decir el barco es de la casa en la orilla, la red se distingue, a pesar de que los polígonos son del mismo color que las elipses. No es una cuestión de color, ya que tanto la elipse como el rectángulo están igualmente pintados al azar.
Cuarta opción
Quizás la red se distingue por rectángulos: corregirlos, distorsionarlos. Es decir la red encuentra fácilmente ambas áreas cerradas independientemente de la forma y descarta la que es un rectángulo. Esta es la hipótesis del autor: la comprobaremos, para lo cual agregaremos no rectángulos, sino polígonos cuadrangulares de forma arbitraria. Y nuevamente, nuestra hipótesis es que la red distingue una elipse de un polígono cuadrangular arbitrario del mismo color.
Por supuesto, puede entrar en el interior de la red y observar las capas y analizar el significado de los pesos y los cambios. El autor está interesado en el comportamiento resultante de la red, el juicio se basará en el resultado del trabajo, aunque siempre es interesante mirar dentro.
hacer cambios en la generación de imágenes def next_pair(): p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p0 = np.rint(np.random.sample()*(radius_max-radius_min) + radius_min) p1 = np.rint(np.random.sample()*(w_size-radius_max)) p2 = np.rint(np.random.sample()*(w_size-radius_max)) p3 = np.rint(np.random.sample()*2.*radius_min - radius_min) p4 = np.rint(np.random.sample()*2.*radius_min - radius_min) p5 = np.rint(np.random.sample()*2.*radius_min - radius_min) p6 = np.rint(np.random.sample()*2.*radius_min - radius_min) p7 = np.rint(np.random.sample()*2.*radius_min - radius_min) p8 = np.rint(np.random.sample()*2.*radius_min - radius_min) poly = np.array(( (p1, p2), (p1+p3, p2+p4+p0), (p1+p5+p0, p2+p6+p0), (p1+p7+p0, p2+p8), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc = list(set(rr) & set(rr_p)) if len(in_sc) > 0: if np.mean(rr_p) > np.mean(in_sc): poly += np.max(in_sc) - np.min(in_sc) else: poly -= np.max(in_sc) - np.min(in_sc) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img = img_l.copy() img[rr, cc] = img_h[rr, cc] img[rr_p, cc_p] = img_h[rr_p, cc_p] else: img = img_h.copy() img[rr, cc] = img_l[rr, cc] img[rr_p, cc_p] = img_l[rr_p, cc_p] msk = np.zeros((w_size, w_size, 1), dtype='float32') msk[rr, cc] = 1. return img, msk
Calculamos imágenes y máscaras y observamos los primeros 10 pares.
construimos cuadros mascaras, elipses y poligonos for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())

Lanzamos nuestra red. Déjame recordarte que es lo mismo para todas las opciones.
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=bce_dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 56s 8ms/step - loss: 0.6815 - my_iou_metric: 0.2168 - val_loss: 0.2078 - val_my_iou_metric: 0.4983
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.1470 - my_iou_metric: 0.6396 - val_loss: 0.1046 - val_my_iou_metric: 0.7784
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0642 - my_iou_metric: 0.8586 - val_loss: 0.0403 - val_my_iou_metric: 0.9354
La hipótesis se confirma, los polígonos y las elipses son fácilmente distinguibles. Un lector atento notará aquí: por supuesto, son diferentes, una pregunta sin sentido, cualquier IA normal puede distinguir una curva de segundo orden de la línea del primero. Es decir la red determina fácilmente la presencia de un límite en forma de curva de segundo orden. No discutiremos, reemplace el óvalo con un heptágono y verifique.
Quinto experimento, el más difícil
No hay curvas, solo caras lisas de heptagones regulares inclinados y rotados y polígonos cuadrangulares arbitrarios. Introducimos en la función los cambios del generador de imágenes / máscaras, solo proyecciones de heptagones regulares y polígonos cuadrangulares arbitrarios del mismo color.
revisión final de la función de generación de imágenes def next_pair(_n = 7): p = np.random.sample() - 0.5 c_x = np.random.sample()*(w_size-2*radius_max) + radius_max c_y = np.random.sample()*(w_size-2*radius_max) + radius_max radius = np.random.sample()*(radius_max-radius_min) + radius_min d = np.random.sample()*0.5 + 1 a_deg = np.random.sample()*360 a_rad = np.deg2rad(a_deg) poly = []
Como antes, construimos matrices y observamos los primeros 10.
construyendo máscaras for k in range(train_num): img, msk = next_pair() train_x[k] = img train_y[k] = msk fig, axes = plt.subplots(2, 10, figsize=(20, 5)) for k in range(10): axes[0,k].set_axis_off() axes[0,k].imshow(train_x[k]) axes[1,k].set_axis_off() axes[1,k].imshow(train_y[k].squeeze())
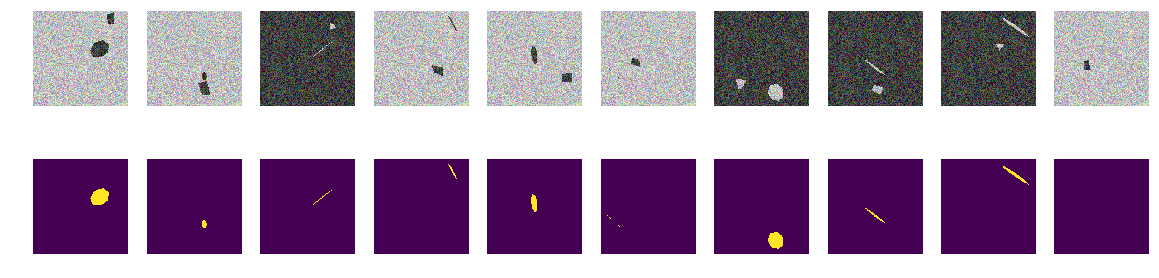
input_layer = Input((w_size, w_size, 3)) output_layer = build_model(input_layer, 16) model = Model(input_layer, output_layer) model.compile(loss=dice_loss, optimizer=Adam(lr=1e-3), metrics=[my_iou_metric]) model.load_weights('./keras.weights', by_name=False) while True: history = model.fit(train_x, train_y, batch_size=32, epochs=1, verbose=1, validation_split=0.1 ) if history.history['my_iou_metric'][0] > 0.75: break
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 54s 7ms/step - loss: 0.5005 - my_iou_metric: 0.1296 - val_loss: 0.1692 - val_my_iou_metric: 0.3722
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.1287 - my_iou_metric: 0.4522 - val_loss: 0.0449 - val_my_iou_metric: 0.6833
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0759 - my_iou_metric: 0.5985 - val_loss: 0.0397 - val_my_iou_metric: 0.7215
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0455 - my_iou_metric: 0.6936 - val_loss: 0.0297 - val_my_iou_metric: 0.7304
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0432 - my_iou_metric: 0.7053 - val_loss: 0.0215 - val_my_iou_metric: 0.7846
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 53s 7ms/step - loss: 0.0327 - my_iou_metric: 0.7417 - val_loss: 0.0171 - val_my_iou_metric: 0.7970
Train on 7372 samples, validate on 820 samples
Epoch 1/1
7372/7372 [==============================] - 52s 7ms/step - loss: 0.0265 - my_iou_metric: 0.7679 - val_loss: 0.0138 - val_my_iou_metric: 0.8280Resumen
Como puede ver, la red distingue entre proyecciones de heptagones regulares y polígonos cuadrangulares arbitrarios con una precisión de 0.828 en el conjunto de prueba. El entrenamiento de la red se detiene con un valor arbitrario de 0,75 y lo más probable es que la precisión sea mucho mejor. Si procedemos de la tesis de que la red encuentra primitivas y sus combinaciones determinan el objeto, entonces en nuestro caso hay dos áreas con un promedio diferente del fondo, no hay primitivas en la comprensión del hombre. No hay líneas obvias de un color, y no hay esquinas, respectivamente, solo áreas con bordes muy similares. Incluso si construye líneas, ambos objetos en la imagen se crean a partir de las mismas primitivas.
Una pregunta para los entendidos: ¿qué considera la red como un signo por el cual distingue "barcos" de "interferencia"? Obviamente, este no es el color o la forma de los bordes de los barcos. Por supuesto, podemos seguir estudiando más esta construcción abstracta de los "mar" / "barcos", no somos la Academia de Ciencias y podemos realizar investigaciones únicamente por curiosidad. Podemos cambiar los heptagones a octágonos o llenar la imagen con ángulos regulares de cinco y seis y ver si su red se distingue o no. Dejo esto a los lectores, aunque también me preguntaba si la red puede contar el número de esquinas del polígono y, para la prueba, organizar no polígonos regulares en la imagen, sino sus proyecciones aleatorias.
Hay otras propiedades no menos interesantes de tales barcos, y tales experimentos son útiles porque nosotros mismos establecemos todas las características probabilísticas del conjunto estudiado y el comportamiento inesperado de redes bien estudiadas agregará conocimiento y traerá beneficios.
Fondo seleccionado al azar, color seleccionado al azar, ubicación del barco / elipse seleccionada al azar. No hay líneas en las imágenes, hay áreas con características diferentes, ¡pero no hay líneas de un solo color! En este caso, por supuesto, hay simplificaciones y la tarea puede complicarse aún más, por ejemplo, elegir colores como 0.0 ... 0.9 y 0.1 ... 1.0, pero para la red no hay diferencia. La red puede y encuentra patrones que son diferentes de los que una persona ve y encuentra claramente.
Si uno de los lectores está interesado, puede continuar investigando y seleccionando en las redes, si lo que no funciona o no está claro, o si aparece un pensamiento nuevo y bueno e impresiona con su belleza, siempre puede compartir con nosotros o preguntar a los maestros (y a los grandes maestros también) y solicite ayuda calificada en la comunidad ODS.