Imagínese: una llamada telefónica a las tres de la mañana, levanta el teléfono y escucha un grito de que nadie más usa su producto. Miedo En la vida, por supuesto, esto no es así, pero si no presta la debida atención al problema de la salida de usuarios, puede encontrarse en una situación similar.
Ya hemos descrito en detalle qué es un flujo de salida: profundizamos en la teoría y mostramos cómo convertir una red neuronal en un oráculo digital. Los expertos de Plarium Krasnodar conocen otra forma de predecir. Hablaremos de él.

Este no es el RFM que necesitamos.
RFM es un método que se utiliza para segmentar clientes y analizar su comportamiento. En función de los datos obtenidos, puede crear un programa de fidelización para cada grupo, crear una distribución de usuarios y predecir cuándo volverán a comprar.
La historia del desarrollo de RFM comenzó en 1987 cuando se publicó el artículo
Contando a sus clientes: quiénes son y qué harán a continuación . Describió un método de análisis basado en la distribución de Pareto (una familia de dos parámetros de distribuciones absolutamente continuas).
El modelo se llamaba Pareto / NBD y solo tenía en cuenta el historial de compras de los usuarios. En la interpretación clásica, el trabajo de este método se basó en cinco pilares, o aproximaciones:
- Mientras los usuarios estén activos, el número de transacciones realizadas por el comprador durante el período t obedece a la distribución de Pareto con un λt promedio.
- La heterogeneidad del parámetro λ (tasa de transacción) sigue una distribución gamma con los parámetros r y α.
- Cada comprador tiene un período ilimitado de tiempo "vida" τ. El punto en el que el usuario se vuelve inactivo se distribuye exponencialmente con el parámetro μ (tasa de abandono).
- La heterogeneidad del parámetro μ entre los usuarios sigue una distribución gamma con los parámetros s (forma) y β (escala).
- Los parámetros λ y μ pueden variar independientemente entre compradores.
Las desventajas de este modelo fueron tanto la alta complejidad del cálculo de las funciones hipergeométricas de Gauss como la búsqueda de la función de máxima verosimilitud.
En un artículo de 2003,
"Contando a sus clientes", la forma fácil: una alternativa al modelo Pareto / NBD , se publicó la idea de implementar un modelo mejor. Además del historial de compras, se usaron dos parámetros más: frecuencia y prescripción. Su principal diferencia con Pareto / NBD fue cómo se determina el momento en que el cliente se va.
En la configuración clásica, se suponía que el usuario podía irse en cualquier momento, independientemente de la frecuencia y el patrón de sus compras en el pasado. El nuevo enfoque se basa en la hipótesis de que el comprador puede comenzar a perder intereses inmediatamente después de que se complete la transacción.
Esto simplificó el cálculo y condujo al modelo beta-geométrico (BG / NBD). Utiliza tres parámetros principales: actualidad, frecuencia, monetario, así como cuatro parámetros adicionales: r, α, a, b (los parámetros ayb se agregaron de la
distribución beta ).
RFM ayuda a predecir si un cliente realizará una compra en el futuro. Los especialistas de Plarium Krasnodar modificaron este método.
Predecir el flujo de salida simple y con buen gusto
Para los cálculos, necesitamos una serie de datos sobre las sesiones de juego. Se recalcula en una matriz que consiste en parámetros RFM y en cuatro coeficientes más, que son seleccionados por el modelo en el proceso de aprendizaje.
En el contexto de un juego, los parámetros adquieren los siguientes significados:
- R ecencia: cuánto tiempo estuvo jugando el usuario en el momento del último inicio de sesión;
- F solicitud: con qué frecuencia el usuario vuelve a ingresar al juego;
- M ontario: cuánto tiempo ha estado jugando el usuario (tiempo de "vida").
Los parámetros se agregan en una matriz. Luego se carga en un modelo que calcula la probabilidad de "vida" de los usuarios, la posibilidad de que continúen jugando.
Los cálculos se realizan de acuerdo con la fórmula:
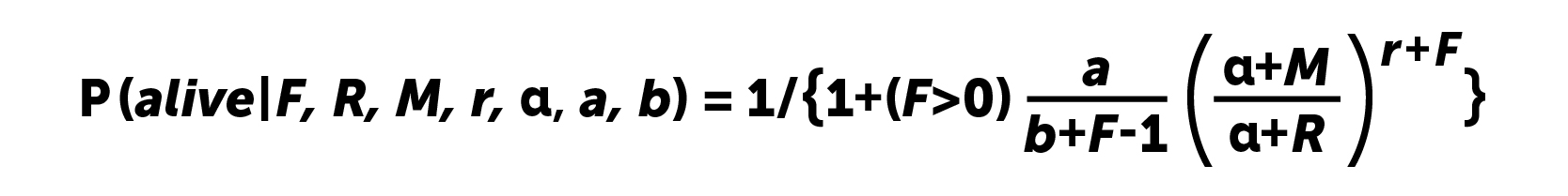
Obviamente, para los usuarios sin reingresos, la probabilidad de "vida" será uno. En 2008, los autores del artículo
Computing P (vivo) Uso del modelo BG / NBD propusieron una solución a este problema. Las compañías de juegos pueden usar dos opciones que dan resultados similares.
Método 1 : se ingresa el parámetro π para todos los usuarios. Muestra qué jugadores se consideran inactivos.
Método 2 : se agrega una unidad al parámetro Frecuencia. Esta medida evita la degeneración de la fórmula en Frecuencia = 0, pero agrega artificialmente una entrada más al juego para cada usuario.
Cómo adaptar el método RFM para desarrolladores de juegos
Supongamos que tenemos un nuevo usuario. Acaba de entrar al juego. Parámetro
F = 1 (o 0, dependiendo de los cálculos), ya que la primera entrada no se considera y el jugador aún no ha tenido entradas repetidas.
El usuario juega tres días. Los parámetros cambian:
F solo tiene en cuenta las entradas diarias, por lo tanto, su valor es 2, y los indicadores
M y
R son 3. Utilizando estos datos, obtenemos la probabilidad de "vida" cercana a la unidad.
Al día siguiente, el usuario no ingresa al juego. El parámetro
M se actualiza, mientras que
F y
R siguen siendo los mismos. Al sustituir todos los valores en la fórmula, vemos que el indicador de probabilidad se ha vuelto más bajo.
Si el usuario no juega durante la semana, el indicador
M se actualiza nuevamente y la probabilidad de "vida" disminuye aún más.
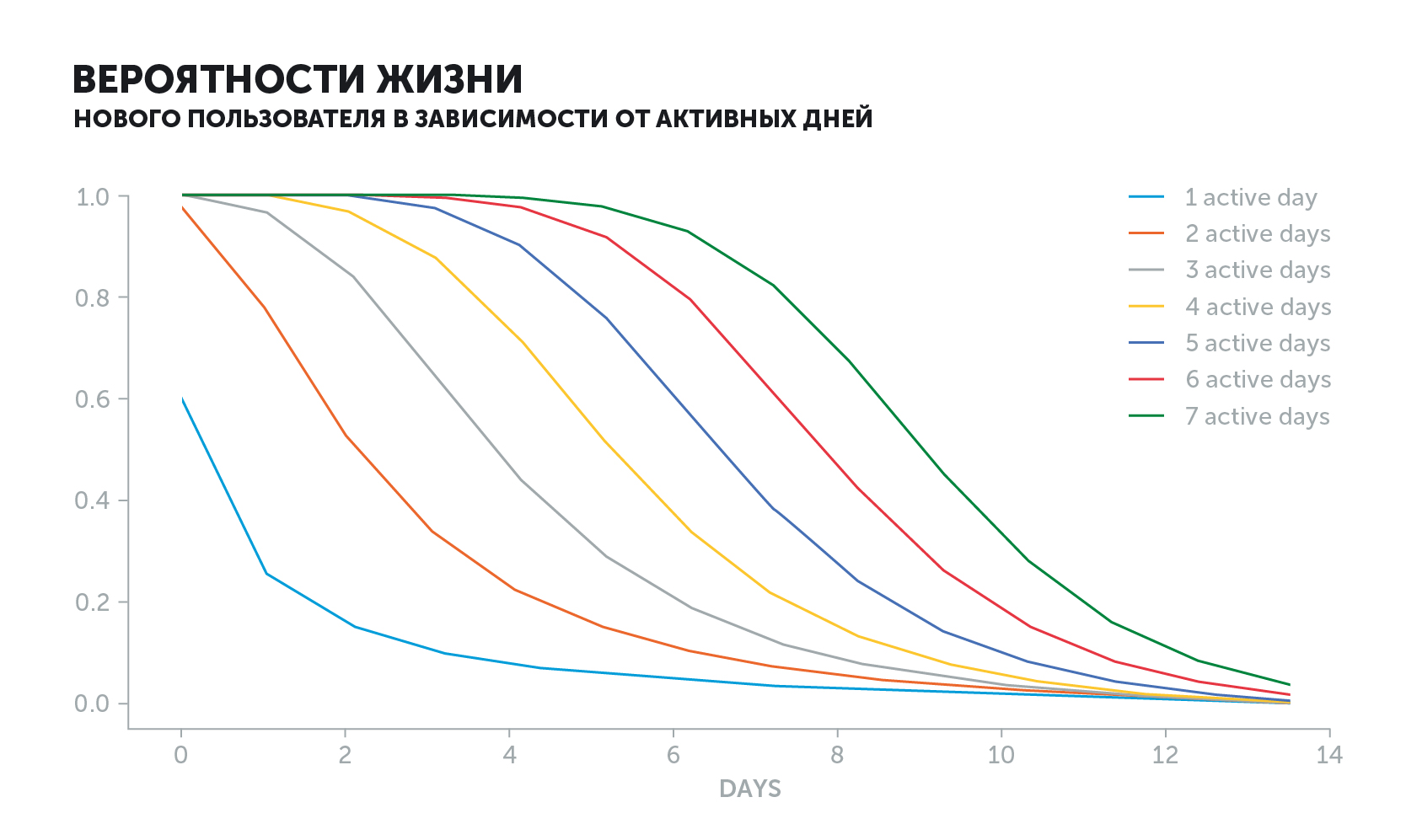
El gráfico del usuario activo se ve diferente. La probabilidad de una "vida" disminuirá dependiendo de su historia. Si entraba al juego todos los días y de repente se detenía, el valor del indicador caerá mucho más rápido que si jugara cada dos días.

Pros importantes y contras obvios de RFM
La principal ventaja de este método es su simplicidad:
- para los cálculos no necesita usar un aparato matemático complejo;
- los indicadores se calculan usando una fórmula relativamente simple;
- Puede prescindir de tuberías complejas para datos;
- Todos los parámetros óptimos del modelo se seleccionan automáticamente.
Además, los datos de RFM son fáciles de interpretar. Al estudiar el historial del usuario, uno puede entender por qué tiene tanta probabilidad de "vida". A menudo, cuando se trabaja con métodos más complejos, es más difícil sacar conclusiones específicas.
RFM también tiene desventajas.
En primer lugar , este no es el método más preciso. Funciona bien, pero no se utilizan varios parámetros en los cálculos. Por ejemplo, muchos usuarios que comienzan a perder interés por hábito ingresan al juego. Es decir, el número promedio de sesiones de juego por día disminuye, y la frecuencia de reingresos no cambia.
En segundo lugar , el método no tiene en cuenta la actividad del usuario: cuántos recursos transfirió, si atacó al enemigo o creó tropas. Si tomamos todos los jugadores con una probabilidad de "vida" igual a ~ 0.8, entonces, dependiendo de los parámetros y su historial, además de los activos, habrá quienes ingresen cada tres días.
En tercer lugar , el usuario fallecido se vuelve "vivo" cuando comienza el juego nuevamente. ¿Qué tiene que hacer esto un mes después del último inicio de sesión? Tales situaciones complican la detección de jugadores con grandes pausas entre sesiones. En general, esto no es crítico, aunque introduce un cierto desequilibrio cuando tratamos de entender si el usuario está "vivo" o no.
¿No es mejor usar una red neuronal?
Mejor, pero antes que nada, necesita comprender cómo implementar el proyecto: resolver tareas a gran escala con un chasquido o avanzar gradualmente hacia el objetivo.
El análisis RFM muestra la probabilidad de la "vida" del usuario en el momento en que se realiza el cálculo. No podremos entender si el jugador se irá en dos o tres semanas, y la red neuronal podrá hacerlo. Dada toda la infraestructura, crear un sistema tan integrado para analizar el comportamiento de los jugadores desde cero es mucho más difícil. Además, necesita una línea de base, con la que pueda comparar la calidad de la red neuronal. Es probable que este enfoque genere pérdidas financieras si no calcula la fortaleza.
Nuestra experiencia muestra que las tareas globales deben implementarse gradualmente. Crear un prototipo funcional no es difícil, pero recopilar y procesar datos, configurar y entrenar una red neuronal es otra cuestión. Estos procesos pueden durar mucho tiempo, lo que siempre falta.
Es por eso que decidimos usar primero un modelo más simple: realizamos una investigación, identificamos los pros y los contras, y lo probamos en el trabajo. Los resultados nos quedaron bien. RFM tiene fallas, pero se compensan generosamente por la facilidad de uso. Y la red neuronal es el siguiente paso hacia la mejora del sistema.