La nueva evidencia, escrita por el escritor australiano de ciencia ficción Greg Egan, y la prueba de 2011, publicada anónimamente en línea, han sido reconocidas como avances significativos en el estudio del misterio que los matemáticos han estado investigando durante 25 años.

El 16 de septiembre de 2011, un fanático del anime publicó una pregunta matemática de 4chan sobre la serie de culto "La
melancolía de Haruhi Suzumiya " en el foro. La primera temporada del programa, donde hubo viajes en el tiempo, se mostró en un orden diferente al cronológico, y durante el programa posterior y el lanzamiento en DVD, el orden de los episodios cambió nuevamente. En Internet, los fanáticos discutieron en qué orden es mejor ver la serie, y el autor de la pregunta preguntó: si la audiencia quisiera ver la serie en todos los órdenes posibles, ¿cuántos episodios estarían en su lista más corta? [se
refiere a una lista en la que puede encontrar cualquier secuencia de episodios / aprox. perev. ]
En menos de una hora, un autor anónimo proporcionó una
respuesta a la pregunta , no una solución completa, sino un límite inferior en el número requerido de episodios. De su razonamiento, aplicable a cualquier número de episodios, se dedujo que durante la primera temporada de Haruhi, que consta de 14 episodios, la audiencia tendría que ver al menos 93,884,313,611 episodios seguidos para estudiar todas las permutaciones posibles. "Examine la evidencia de fallas que podría haber pasado por alto", escribió el autor de la respuesta.
Durante siete años, la prueba pasó desapercibida en la comunidad matemática: resultó que en ese momento solo un matemático profesional lo notó y no lo estudió lo suficientemente a fondo. Sin embargo, de repente el mes pasado, el escritor australiano de ciencia ficción
Greg Egan demostró un nuevo
límite superior en la cantidad de episodios necesarios. El descubrimiento de Egan volvió a despertar el interés en la tarea y llamó la atención sobre el registro relativo al límite inferior de 2011. Ambas evidencias ahora se consideran avances significativos en el estudio del misterio que los matemáticos han estado investigando durante al menos 25 años.
Los matemáticos verificaron rápidamente el límite superior de Egan, que, como el límite inferior, es aplicable a secuencias de cualquier longitud. Luego Robin Houston, matemático en visualización de datos en Kiln, y
Jay Panton de la Universidad Marquette en Milwaukee confirmaron de forma independiente el trabajo de un autor anónimo con 4chan. "Se hizo un gran esfuerzo para verificar la validez de esta hipótesis", dijo Panton, ya que las ideas clave de la prueba no se expresaron con suficiente claridad.
Y ahora, Houston y Panton, junto con
Vince Vater de la Universidad de Florida, han escrito un
trabajo formal . En él, indicaron al primer autor como "un cartel anónimo de 4chan".
"Lo extraño es que esta prueba muy elegante de un hecho previamente desconocido apareció en un lugar tan poco probable", dijo Houston.
Ciudades de permutaciones
Si la serie tiene solo tres episodios, hay seis formas posibles de verlos: 123, 132, 213, 231, 312 y 321. Pueden unirse y hacer una lista de 18 episodios, incluida cada versión del pedido. Sin embargo, también existe un método de pegado más eficiente: 123121321. Dicha secuencia que contiene todas las permutaciones de un conjunto de n caracteres se denomina superpermutación.
En 1993, Daniel Ashlock y Janet Tilotson descubrieron que al estudiar las supermutaciones más cortas para varios valores de n, los factores comienzan a aparecer rápidamente, ¡los mismos valores escritos en la forma n!, Es decir, multiplicando todos los números de 1 a n (por ejemplo, 4 ! = 4 * 3 * 2 * 1).
Si solo hay 1 episodio en tu serie, ¡la duración de la superpermutación más corta será 1! (También conocido como la buena unidad antigua). Para una serie de dos episodios, la superpermutación más corta (121) tiene una duración de 2. + 1! .. Para tres episodios (ejemplo anterior), ¡la duración es 3! + 2! + 1!, Y para cuatro episodios (123412314231243121342132413214321) ¡serán 4! + 3! + 2! + 1! .. La regla factorial se ha aceptado generalmente (aunque nadie pudo probar que es cierto para todos los n), y los matemáticos posteriores lo confirmaron para n = 5.
Luego, en 2014, Houston impresionó a los matemáticos,
mostrando que para n = 6 la regla dejó de funcionar. La regla predice que se necesitarán 873 episodios para ver seis episodios de todas las formas posibles, pero Houston encontró la manera de hacerlo en 872. Y dado que hay una manera simple de convertir una superpermutación corta para n caracteres en una superpermutación corta para n + 1 caracteres, el ejemplo de Houston significa que la regla factoriales no funciona para todos n> 6.
El edificio Houston convierte la tarea de la superpermutación en el famoso problema del vendedor ambulante, que busca el camino más corto a través de varias ciudades. Específicamente, las superpermutaciones están asociadas con el problema del vendedor "asimétrico", en el que cada camino entre dos ciudades tiene su propio precio (no necesariamente el mismo en ambas direcciones), y el objetivo es encontrar el camino más barato a través de todas las ciudades.
Esta transformación es fácil de entender: imagine que cada permutación es una ciudad e imagine el camino desde cada permutación a cualquier otra permutación. En el problema de la superpermutación, necesitamos la secuencia de dígitos más corta en la que estén presentes todas las permutaciones, por lo que nuestro objetivo es pasar por todas las permutaciones para agregar el menor número posible a la permutación inicial. Anunciamos que el costo de cada ruta es simplemente el número de dígitos que necesitamos adjuntar al final de la primera permutación para obtener la segunda. En el ejemplo con n = 3, la ruta de 231 a 312 cuesta $ 1, ya que necesitamos agregar solo 2 al final de 231 para obtener 312, y la ruta de 231 a 132 cuesta $ 2, ya que necesitamos agregar 32. En tal formulación, la forma más barata de Todas las ciudades corresponden directamente a la superpermutación más corta.
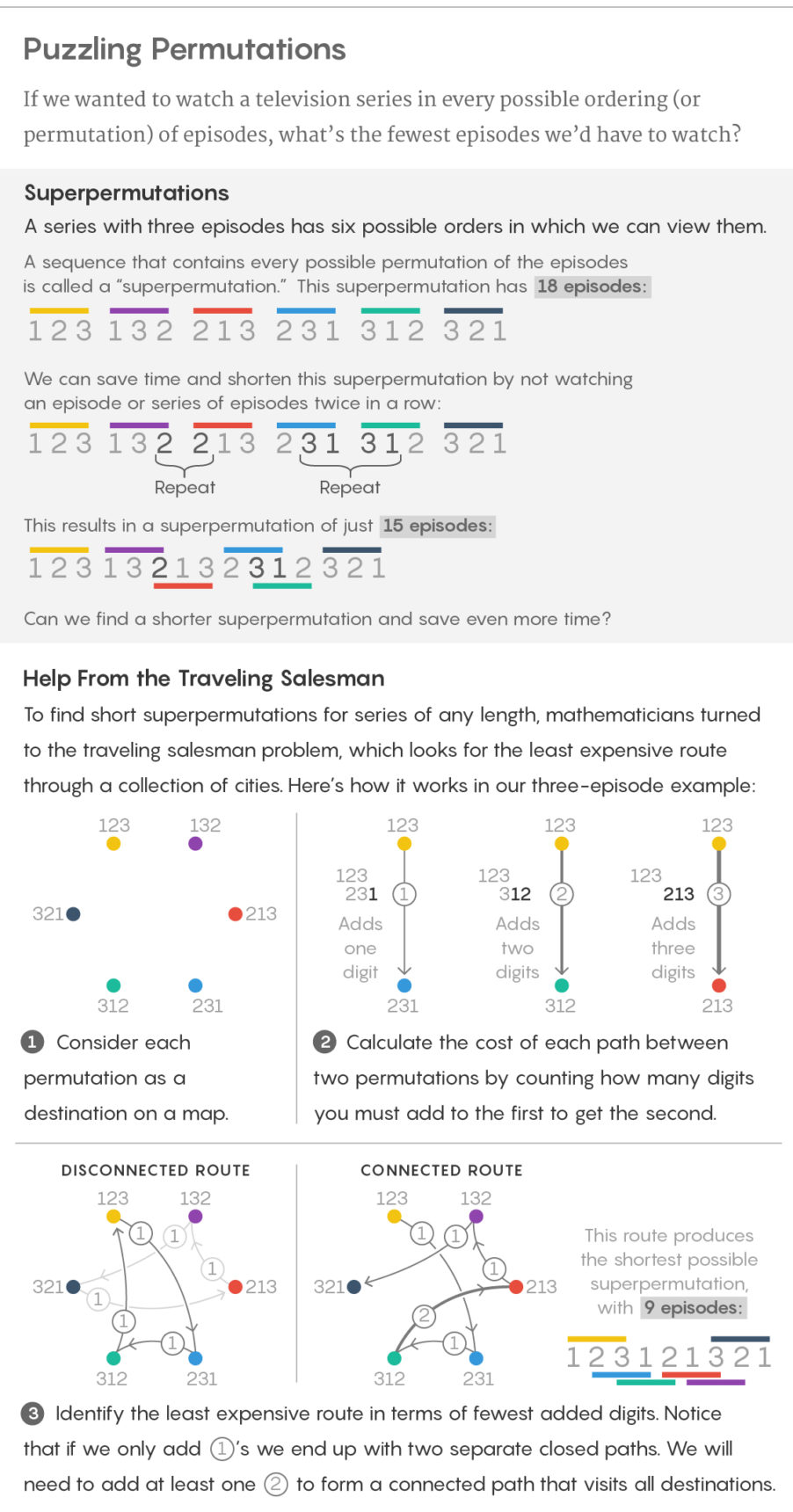
Tal transformación significó que Houston podría dirigir todas las capacidades de los algoritmos para resolver el problema del vendedor ambulante al problema de la superpermutación. Este problema es conocido por pertenecer a la clase de los complejos NP, lo que significa la ausencia de un algoritmo efectivo que pueda resolverlo en el caso general. Sin embargo, existen algoritmos que pueden resolver eficazmente algunas variedades del problema, y otros algoritmos pueden producir buenas soluciones aproximadas. Houston usó uno de estos últimos para emitir una superpermutación de 872 dígitos de longitud.
Como solo dio una solución aproximada, puede que ni siquiera sea la superpermutación más ideal. Los matemáticos ahora están realizando una voluminosa búsqueda computacional para la permutación más corta de 6 caracteres, dijo Panton. "Sabemos que nuestras búsquedas terminarán en un tiempo limitado, pero no sabemos si tomará una semana o un millón de años", dijo. "No hay barra de progreso".
Orden incorrecta
Cuando apareció el trabajo de Houston, una publicación anónima en 4chan había estado en su rincón de Internet durante casi tres años. Un matemático,
Nathaniel Johnston de la Universidad Mount Ellison, notó una copia de esta publicación en otro sitio unos días después de que apareció esta publicación, y no porque fuera un amante del anime, sino porque ingresó varias solicitudes en Google, asociado con superpermutaciones.
Johnston leyó la evidencia y le pareció confiable, pero no desperdició su energía en un examen exhaustivo. En ese momento, los matemáticos creían que la fórmula factorial para las superpermutaciones probablemente era correcta, y cuando crees que sabes la respuesta exacta a la pregunta, no estás interesado en el límite inferior de la estimación. En otras palabras, los episodios de la serie sobre superpermutaciones fueron en el orden incorrecto.
Después de eso, Johnston mencionó el límite inferior en un
par de sitios web , pero "no creo que nadie haya prestado especial atención a esto", dijo.
Luego, el 26 de septiembre de 2018, el matemático
John Baez de la Universidad de California en Riverside tuiteó una
publicación sobre el descubrimiento de Houston en 2014, como parte de una serie de tweets sobre patrones matemáticos obvios que dejan de funcionar.
Nota perev .: no hubo una serie tan grande de tweets, solo tres. Los otros dos también son interesantes en sí mismos, aunque no están relacionados con este artículo. Uno dice que 6 es la distancia más popular entre dos números primos adyacentes para todos los números primos menores de 17,427,000,000,000,000,000,000,000,000,000. ¡Y entonces este patrón deja de funcionar de repente! El segundo demuestra la siguiente conexión de integrales, funciones trigonométricas y el número π

¡Pero solo para n <9.8 × 10 42 !Su tweet llamó la atención de Egan, que estudió matemáticas hace varias décadas, antes de que comenzara su carrera como escritor de ciencia ficción reconocido (su primera historia exitosa, por casualidad, se llamaba "La ciudad de las permutaciones"). "Nunca dejé de interesarme por las matemáticas", escribió Egan por correo.
Egan se preguntó si sería posible crear una superpermutación aún más corta que la de Houston. Se sumergió en el estudio de la literatura sobre cómo crear atajos en redes de permutaciones, y después de unas semanas encontró lo que necesitaba. En un par de días, dedujo un nuevo límite superior en la longitud de la superpermutación más corta de n caracteres: n! + (n - 1)! + (n - 2)! + (n - 3)! + n - 3. Es similar a la fórmula factorial, de la cual se excluyeron muchos miembros.
"Rompió por completo el límite superior anterior", dijo Houston.
El límite inferior del autor de la publicación en 4chan estaba seductoramente cerca del nuevo límite superior: n! + (n - 1)! + (n - 2)! + n - 3. Después de la publicación del resultado, Egan Johnston recordó a los matemáticos la prueba de un autor anónimo, y Houston y Panton pronto demostraron su exactitud. Al igual que en el trabajo de Houston, los nuevos límites inferior y superior son adecuados para las superpermutaciones desde el punto de vista del problema del vendedor ambulante: el límite inferior muestra que el camino a través de todas las ciudades debe pasar por un número mínimo de caminos que valen más de $ 1, y el límite superior crea un camino especial para cada n, utilizando solo compuestos por valor de $ 1 y $ 2.
Ahora, los investigadores están tratando de unir los límites superior e inferior, y encontrar una fórmula única que resuelva el problema de la superpermutación. "Probablemente, al final, la gente todavía resolverá este enigma", predijo Báez. "Ahora todo se ve bien".
Para los fanáticos de Haruhi, la solución de Egan brinda instrucciones precisas sobre cómo ver todas las opciones posibles para la primera temporada con un total de 93,924,230,411. Puede comenzar a mirar hoy, o puede esperar hasta que los matemáticos puedan reducir este número. El límite inferior de un autor anónimo demuestra que este recorte no les ahorrará más de 40 millones de episodios; sin embargo, esto es suficiente para comenzar a prepararse para la segunda temporada.