🕐 🐷 🤜🏼 Acelerómetros y giroscopios MEMS: comprensión de las especificaciones 🚳 👨🏾‍🍳 🏭

"Houston, tenemos problemas", llegó una voz cansada en mi cerebro, tratando de pasar la hoja de datos InvenSense IMU MPU-9250 por la noche. Cuando todas las palabras individualmente son entendibles, pero su relación se confunde con la imposibilidad. Todo comenzó con el parámetro LSB, sobre el cual solo recordaba vagamente que, en la traducción, era el bit menos significativo. Luego fue "Resolución", "Sensibilidad", y aún más me di cuenta de que el texto resultante ya puede titularse "Hoja de datos para tontos".

Un poco sobre los bloques principales del módulo de inercia.

Giroscopio MEMS

El MPU-9250 consta de tres sensores de velocidad angular vibracionales uniaxiales independientes (giroscopios MEMS) que responden a la rotación alrededor de los ejes X, Y, Z. Dos masas suspendidas oscilan en ejes opuestos. Con el advenimiento de la velocidad angular, el efecto Coriolis provoca un cambio en la dirección de la vibración (

v e c F_{K} = - 2 m [v e c o m e g a t i m e s v e c v_{r}]

$\ vec {F} _K = -2m [\ vec {\ omega} \ times \ vec {v} _r]$ que se fija mediante un sensor capacitivo. El componente capacitivo diferencial medido es proporcional al ángulo de movimiento [Tiempo electrónico]. La señal resultante se amplifica, demodula y filtra, dando como resultado un voltaje proporcional a la velocidad angular de rotación. Esta señal se digitaliza utilizando el ADC de 16 bits incorporado. La frecuencia de muestreo puede variar programáticamente de 3.9 a 8000 muestras por segundo (muestras por segundo, SPS), y los filtros de paso bajo (LPF) definidos por el usuario proporcionan una amplia gama de posibles frecuencias de corte. El filtro de paso bajo es necesario, en particular, para eliminar las vibraciones de los motores (como regla, por encima de 20-25 Hz).

Acelerómetro MEMS de tres ejes

Utiliza una masa de prueba separada para cada eje, que cambia cuando ocurre la aceleración a lo largo de este eje (fijada por sensores capacitivos). La arquitectura MPU-9250 reduce la exposición a la deriva de temperatura y las variaciones en los parámetros eléctricos. Cuando el dispositivo se encuentra en una superficie plana, medirá 0g a lo largo de los ejes X e Y y + 1g a lo largo del eje Z. El factor de escala ( factor de escala: la relación entre el cambio en la señal de salida y el cambio en la señal medida de salida) se calibra en la fábrica y no depende de la tensión de alimentación. Cada sensor está equipado con un ADC sigma-delta individual (consta de un modulador y un filtro digital de paso bajo, más información sobre el dispositivo en [Easyelectronics]), cuya salida digital tiene un rango de medición ajustable.

Y casi el magnetómetro MEMS de tres ejes

Basado en tecnología de efecto Hall de alta precisión. Incluye sensores magnéticos que determinan la intensidad del campo magnético de la tierra a lo largo de los ejes, un circuito de control, un circuito de amplificación de señal y un circuito computacional para procesar señales de cada sensor. Cada ADC tiene una resolución de 16 bits, un rango de medición

p m 4800 m u T

$\ pm 4800 \ mu T$ . Para medir campos magnéticos débiles, se utiliza una unidad en el sistema SI microtesley (μT) o gauss (sistema G, GHS):

1 G . = 100 m u T

$1 G. = 100 \ mu T$ , [Piloto de radio]).

Entonces, ¿qué es LSB y cómo calcularlo? Instrucciones de producción

Digamos que nuestro acelerómetro ahora está operando en el rango de medición

F S = p m 2 g

$FS = \ pm 2g$ , es decir, el rango completo de valores posibles será

2 c d o t F S = 4 g

$2 \ cdot FS = 4g$ . Los valores de voltaje correspondientes se digitalizan mediante un ADC de 16 bits, que puede dividir todo el intervalo tanto como sea posible

2^{16} = 65536

$2 ^ {16} = 65536$ pasos El incremento mínimo que se puede detectar es solo un paso

L S B = 2 c d o t F S / 65536

$LSB = 2 \ cdot FS / 65536$ . Aquí debemos recordar que la cuenta se realiza desde cero, de modo que, de hecho, el valor máximo medido será

2 c d o t F S_{t r u e} = (2^{16} - 1) * L S B = 65535 * L S B = 2 c d o t F S - L S B

$2 \ cdot FS_ {true} = (2 ^ {16} - 1) * LSB = 65535 * LSB = 2 \ cdot FS - LSB$ . Es decir, cuantos más bits hay en una palabra digital ADC o DAC, menor es la discrepancia. En este caso, la sensibilidad (a veces llamada factor de escala, factor de escala de sensibilidad) del sensor en un rango específico se determinará como la relación de la señal de salida eléctrica y el impacto mecánico. Tradicionalmente indicado para una frecuencia de señal de 100 Hz y temperatura

T = + 25^{c i r c} C .

$T = + 25 ^ {\ circ} C.$ Para el MPU-9250, la sensibilidad es

2^{16} / (2 c d o t F S)

$2 ^ {16} / (2 \ cdot FS)$ pasos para cada go

^{c i r c} / s

$^ {\ circ} / s$ (

L S B / g

$LSB / g$ ,

L S B / (^{c i r c} / s)

$LSB / (^ {\ circ} / s)$ ), para otra IMU, BMI088 de Bosch Sensortec, la sensibilidad del giroscopio se calcula de la misma manera, y para el acelerómetro se utiliza

(2^{16} - 2^{4}) / (2 c d o t F S)

$(2 ^ {16} -2 ^ 4) / (2 \ cdot FS)$ pasos para cada g.

Sacamos las variantes FS de la especificación para giroscopios y, para no levantarnos dos veces, acelerómetros.

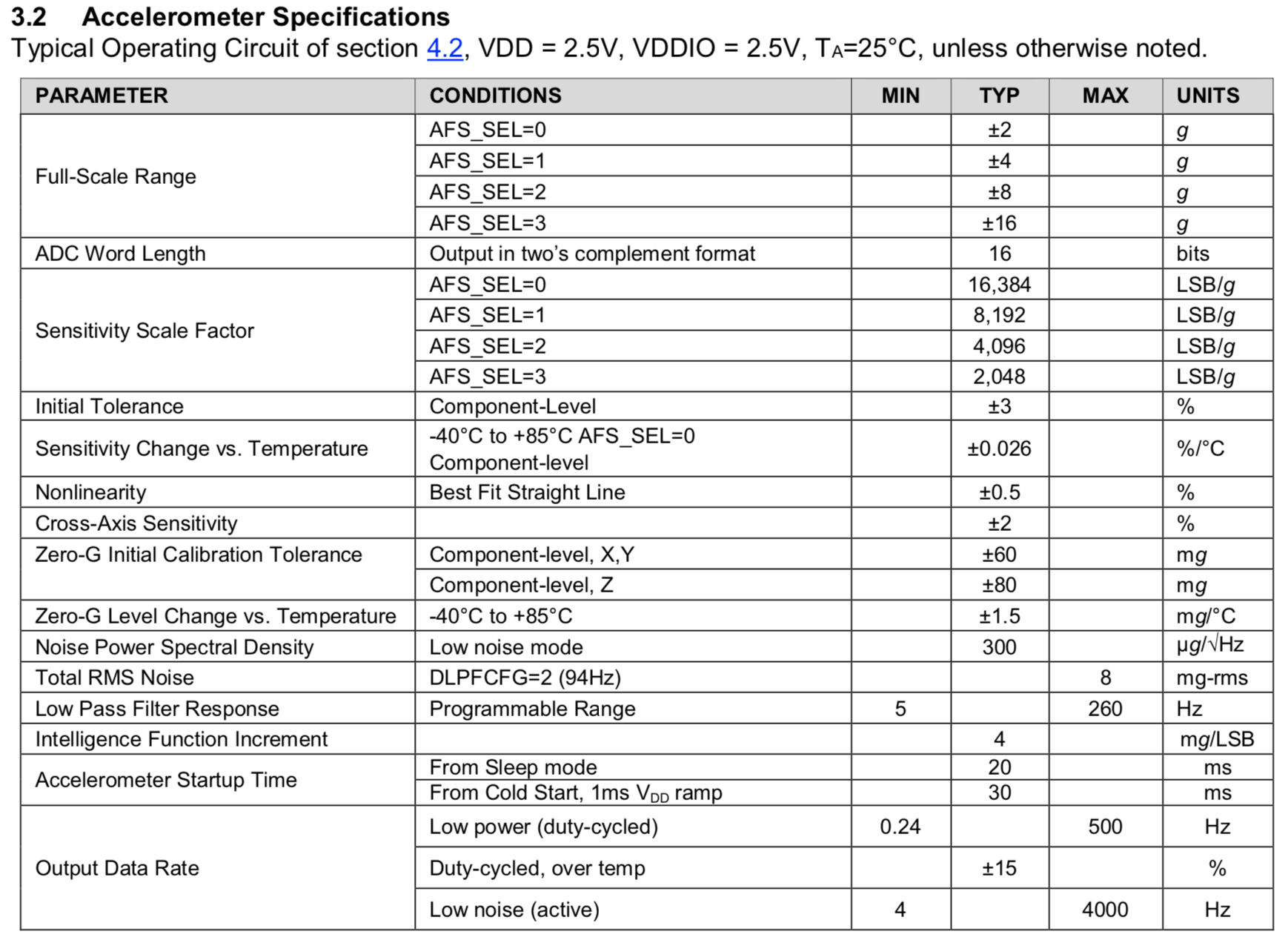
También tomé FS para acelerómetros de la documentación para BMI088 (ver más abajo).

Giroscopio, 16 bit $(2 ^ N = 65535)$		Acelerómetro, 16 bit $(2 ^ N = 65535)$
Rango (FS) $^ {\ circ} / s$ (dps)	LSB, $^ {\ circ} / s$ (dps)	Rango (FS), g	LSB mg
$\ pm 125$ (FS = 250)	0.004	$\ pm 2$ (FS = 4)	0,06
$\ pm 250$ (FS = 500)	0.008	$\ pm 3$ (FS = 6)	0,09
$\ pm 500$ (FS = 1000)	0.0015	$\ pm 4$ (FS = 8)	0,12
$\ pm 1000$ (FS = 2000)	0,03	$\ pm 6$ (FS = 12)	0,18
$\ pm 2000$ (FS = 4000)	0,06	$\ pm 8$ (FS = 16)	0.24
		$\ pm 12$ (FS = 24)	0,37
		$\ pm 16$ (FS = 32)	0,48
		$\ pm 24$ (FS = 48)	0,73

Parece que todo encajó, puedes seguir adelante. En algunos casos (a continuación, por ejemplo, un recorte de la documentación para BMI088), un parámetro como la resolución se indica por separado.

De hecho, parece que debería ser un LSB. Pero, ¿por qué entonces vemos un valor en lugar de varios vinculados a rangos específicos? Tuve que ampliar la lista de fuentes estudiadas en busca de respuestas.

¿Qué es la resolución?

El valor mínimo que el sensor ve de manera confiable es extremadamente importante cuando se trata de lograr un equilibrio entre precio y rendimiento. Esto no es precisión: un sensor de alta resolución puede no ser particularmente preciso, al igual que un sensor de baja resolución en ciertas áreas puede tener suficiente precisión. Desafortunadamente, el LSB solo define el valor teórico mínimo distinguible, siempre que podamos usar los 16 bits del ADC. Esta es una resolución en el mundo digital. En analógico, algunos de los pasos serán ruidosos y la cantidad de bits efectivos será menor.

¿Cuáles son las características del ruido y de dónde proviene?

Las fuentes de ruido generalmente se pueden dividir en ruido electrónico de un circuito que convierte el movimiento en una señal de voltaje (ruido térmico Johnson, ruido de disparo, ruido de parpadeo rosa 1 / f, etc.) y mecánico mecánico (browniano, debido a la presencia de pequeñas piezas móviles) desde el propio sensor. Las características de este último dependerán de la frecuencia de resonancia de la parte mecánica del sistema.

f_{0}

$f_0$ (frecuencia de oscilación natural del sensor

o m e g a_{0} = 2 p i / f_{0}

$\ omega_0 = 2 \ pi / f_0$ )

Ruido RMS en todo el rango espectral - Ruido total RMS (raíz cuadrada media)

Los niveles de ruido se pueden determinar de varias maneras. Puede considerarlos en el dominio de tiempo o frecuencia (después de la transformación de Fourier). En el primer caso, el ruido residual se toma como el valor eficaz de las señales del sensor fijo (de hecho, esta es la desviación estándar para el muestreo en

o v e r l i n e x = 0

$\ overline x = 0$ ) por un cierto período de tiempo:

x_{R M S} = s i g m a_{X} = s q r t s u m_{i = 1}^{n} {(x_{i} - o v e r l i n e x)}^{2} o v e r n - 1

$x_ {RMS} = \ sigma_X = \ sqrt {\ sum_ {i = 1} ^ n {(x_i - \ overline x)} ^ 2 \ over {n-1}}$

Las aceleraciones o velocidades de rotación angular inferiores al nivel de ruido de banda ancha serán indistinguibles: esta es la resolución real. El valor eficaz de un voltaje o corriente alterna (a menudo denominado activo o efectivo) es igual al valor de una señal constante cuya acción realizará el mismo trabajo en una carga activa (resistiva) durante el período. Este enfoque es más efectivo cuando se evalúa el ruido de banda ancha, donde predomina el ruido blanco.

Para el ruido blanco, la relación de amplitud (valor de pico instantáneo) a rms con una probabilidad de 99.9% es

N_{P P} / N_{R M S} = 6.6.

$N_ {PP} / N_ {RMS} = 6.6.$ Esta relación se llama factor cruzado (factor de cresta, relación cruzada). Puede elegir una probabilidad del 95.5%: el factor cruzado será 4.

De hecho, las señales de ruido no se comportan tan bien y pueden producir picos que aumentan el factor cruzado hasta 10 veces. En algunas especificaciones puedes encontrar los valores

N_{P P}

$N_ {PP}$ o el multiplicador en sí.

En una banda estrecha de baja frecuencia de 0.1–10 Hz, el ruido principal “1 / f” desempeña el papel principal, que se estima utilizando la amplitud de la señal de ruido de pico a pico.

Densidad espectral

A veces es más conveniente considerar una señal en el dominio de la frecuencia, donde su descripción se llama espectro (la dependencia de la amplitud y la fase de la frecuencia). Una de las posibles características del ruido en las especificaciones se denomina densidad espectral de ruido (PSD), densidad espectral de ruido, densidad de potencia de ruido o simplemente densidad de ruido ). Describe la distribución de la potencia de ruido en un rango de frecuencia. Independientemente de la representación de la señal eléctrica a través de la corriente o el voltaje, la potencia instantánea disipada en la carga puede normalizarse (R = 1 Ohm) y expresarse como

p (t) = {n u}^{2} (t) / R = i^{2} (t) R = x^{2} (t) .

$p (t) = {\ nu} ^ 2 (t) / R = i ^ 2 (t) R = x ^ 2 (t).$ Potencia media disipada por la señal durante un período de tiempo

(- T / 2, T / 2),

$(- T / 2, T / 2),$

P_{x}^{T} = f r a c 1 T i n t_{- T / 2}^{T / 2} x^{2} (t) d t .

$P_x ^ T = \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$

El poder es la tasa de entrada de energía. Las señales determinadas y no periódicas se determinan a través de la energía. Las señales periódicas y aleatorias se expresan en términos de potencia, ya que no están limitadas en tiempo y, en consecuencia, en energía, y en un momento dado su potencia promedio es distinta de cero

P_{x} = l i m_{T t o i n f t y} f r a c 1 T i n t_{- T / 2}^{T / 2} x^{2} (t) d t .

$P_x = \ lim_ {T \ to \ infty} \ frac {1} {T} \ int ^ {T / 2} _ {- T / 2} x ^ 2 (t) \, dt.$

Puede recordar [Sklyar] que una señal periódica arbitraria se expresa mediante una combinación de un número infinito de armónicos con frecuencias crecientes:

x (l a m b d a) = f r a c a_{0} 2 + s u m_{n = 1}^{i n f t y} (a_{n} c o s n l a m b d a + b_{n} s i n n l a m b d a),

$x (\ lambda) = \ frac {a_0} {2} + \ sum_ {n = 1} ^ {\ infty} (a_n \ cos n \ lambda + b_n \ sin n \ lambda),$

que después de representar el coseno y el seno en forma exponencial

c o s l a m b d a = f r a c e^{i l a m b d a} + e^{- i l a m b d a} 2, s i n l a m b d a = f r a c e^{i l a m b d a} - e^{- i l a m b d a} 2 i

$\ cos \ lambda = \ frac {e ^ {i \ lambda} + e ^ {- i \ lambda}} {2}, \ sin \ lambda = \ frac {e ^ {i \ lambda} - e ^ {- i \ lambda}} {2i}$

y reemplazos

l a m b d a = o m e g a t = 2 p i f_{0} t = f r a c 2 p i t T_{0}

$\ lambda = \ omega t = 2 \ pi f_0 t = \ frac {2 \ pi t} {T_0}$ se puede escribir como

x (t) = f r a c a_{0} 2 + f r a c 12 s u m_{n = 1}^{i n f t y} [(a_{n} - i b_{n}) e^{i n o m e g a t} + (a_{n} + i b_{n}) e^{- e n o m e g a t}] = s u m_{n = - i n f t y}^{i n f t y} c_{n} e^{e n o m e g a t},

$x (t) = \ frac {a_0} {2} + \ frac {1} {2} \ sum_ {n = 1} ^ {\ infty} [(a_n - ib_n) e ^ {in \ omega t} + (a_n + ib_n) e ^ {- en \ omega t}] = \ sum_ {n = - \ infty} ^ {\ infty} c_n e ^ {en \ omega t},$

¿Dónde están los coeficientes complejos (componentes espectrales) de la serie de Fourier para

x (t)

$x (t)$ ,

$$ display $$ \ begin {ecation} c_n = \ frac {1} {T_0} \ int ^ {T_0 / 2} _ {- T_0 / 2} x (t) e ^ {- in \ omega t}, dt = \ begin {cases} \ frac {1} {2} (a_n-ib_n), & n> 0 \\ \ frac {a_0} {2}, & n = 0 \\ \ frac {1} {2} ( a_n + ib_n), & n <0 \ end {cases} \ end {ecation} $$ display $$En el caso general, estos coeficientes son representables de la siguiente manera:

c_{n} = | c_{n} | e^{i t h e t a_{n}},

$c_n = | c_n | e ^ {i \ theta_n},$

| c_{n} | = f r a c 12 s q r t a_{n}^{2} + b_{n}^{2}, t h e t a_{n} = a r c t a n l e f t (f r a c b_{n} a_{n} r i g h t), b_{0} = 0, c_{0} = f r a c a_{0} 2 .

$| c_n | = \ frac {1} {2} \ sqrt {a_n ^ 2 + b_n ^ 2}, \ theta_n = \ arctan \ left (\ frac {b_n} {a_n} \ right), b_0 = 0, c_0 = \ frac {a_0} {2}.$

La amplitud y el espectro de fase se denominan gráficos de dependencia.

| c_{n} |

$| c_n |$ y

t h e t a_{n}

$\ theta_n$ de frecuencia Densidad espectral de potencia

P S D (f)

$PSD (f)$ señal periódica

x (t)

$x (t)$ da la distribución de la potencia de la señal en un rango de frecuencia:

P S D (f) = s u m_{n = - i n f t y}^{i n f t y} | c_{n} |^{2} d e l t a (f - n f_{0})

$PSD (f) = \ sum ^ {\ infty} _ {n = - \ infty} | c_n | ^ 2 \ delta (f-nf_0)$

y tiene dimensión

[W / H z] = [x^{2} / H z] .

$[W / Hz] = [x ^ 2 / Hz].$ La potencia normalizada promedio de la señal real será

P_{x} = i n t_{- i n f t y}^{i n f t y} P S D (f), d f .

$P_x = \ int ^ {\ infty} _ {- \ infty} PSD (f), df.$

Las señales aleatorias no periódicas (en particular, el ruido) pueden describirse como periódicas en el sentido limitante. Si

T_{0}

$T_0$ tiende al infinito, la secuencia de impulsos se convierte en un impulso separado

x (t)

$x (t)$ , el número de líneas espectrales tiende al infinito, el gráfico del espectro se convierte en un espectro de frecuencia suave

X (f) .

$X (f).$ Para este caso límite, podemos determinar un par de transformadas integrales de Fourier

X (f) = i n t_{- i n f t y}^{i n f t y} x (t) e^{- i 2 p i f t}, d t

$X (f) = \ int ^ {\ infty} _ {- \ infty} x (t) e ^ {- i 2 \ pi f t}, dt$

x (t) = i n t_{- i n f t y}^{i n f t y} X (f) e^{i 2 p i f t}, d f,

$x (t) = \ int ^ {\ infty} _ {- \ infty} X (f) e ^ {i 2 \ pi f t}, df,$

donde

X (f)

$X (f)$ - Imagen de Fourier.

La densidad espectral de potencia de una señal aleatoria se determina a través del límite.

P S D (f) = l i m_{T t o i n f t y} f r a c 1 T | X_{T} (f) |^{2} .

$PSD (f) = \ lim_ {T \ to \ infty} \ frac {1} {T} | X_T (f) | ^ 2.$

y describe la distribución de la potencia de la señal en el rango de frecuencia.

Dado que suponemos que el promedio del ruido blanco de los sensores en un estado estacionario es cero (

o v e r l i n e x = o v e r l i n e x^{2} = 0

$\ overline x = \ overline x ^ 2 = 0$ ), entonces el cuadrado del valor eficaz es igual a la varianza y representa la potencia total en la carga normalizada:

R u i d o_{R M S}^{2} = s i g m a_{x}^{2} = P_{x} = i n t_{0}^{i n f t y} P S D (f), d f = i n t_{0}^{A n c h o d e b a n d a} P S D (f), d f = P S D (B a d n w i d t h - 0) $

$Ruido_ {RMS} ^ 2 = \ sigma_x ^ 2 = P_x = \ int ^ {\ infty} _0 PSD (f), df = \ int ^ {Ancho de banda} _0 PSD (f), df = PSD (Badnwidth - 0) $$

N o i s e R M S = s q r t D e n s i d a d d e r u i d o v e c e s e l a n c h o d e b a n d a

$Noise RMS = \ sqrt {Densidad de ruido \ veces el ancho de banda}$

Nos fijamos en la especificación: allí, de hecho, la raíz cuadrada de la misma con la dimensión correspondiente se indica bajo el nombre de densidad espectral

[^{c i r c} / s / s q r t H z]

$[^ {\ circ} / s / \ sqrt {Hz}]$ o

[m u g / s q r t H z] .

$[\ mu g / \ sqrt {Hz}].$ Es decir, el valor del ruido RMS sin indicar la banda de frecuencia en la que se leyó (Ancho de banda) no tiene sentido.

Un poco más sobre la elección del ancho de banda

A la salida del sensor MEMS, obtenemos señales de diferentes frecuencias. Se supone que tenemos una cierta idea de los procesos que estamos midiendo de antemano. Por ejemplo, al determinar el vector de aceleración de un dron, el ruido es la vibración del dispositivo. Puede separarlos de la señal útil utilizando un filtro de paso bajo que corta todas las frecuencias por encima de la especificada (por ejemplo, 200 Hz). El MPU-9250 proporciona la capacidad de ajustar la frecuencia de corte del filtro de paso bajo utilizando el parámetro con el nombre mágico DLPFCFG . Es sinónimo de configuración de filtro digital de paso bajo. Más adelante en la especificación, surgieron expresiones no menos misteriosas del tipo (DLPFCFG = 2, 92Hz) aquí y allá, pero para decodificar tuve que subir a otro documento, "Registrar mapa y descripciones". Muestra qué conjuntos de bits en los que se deben escribir los registros para lograr los efectos deseados:

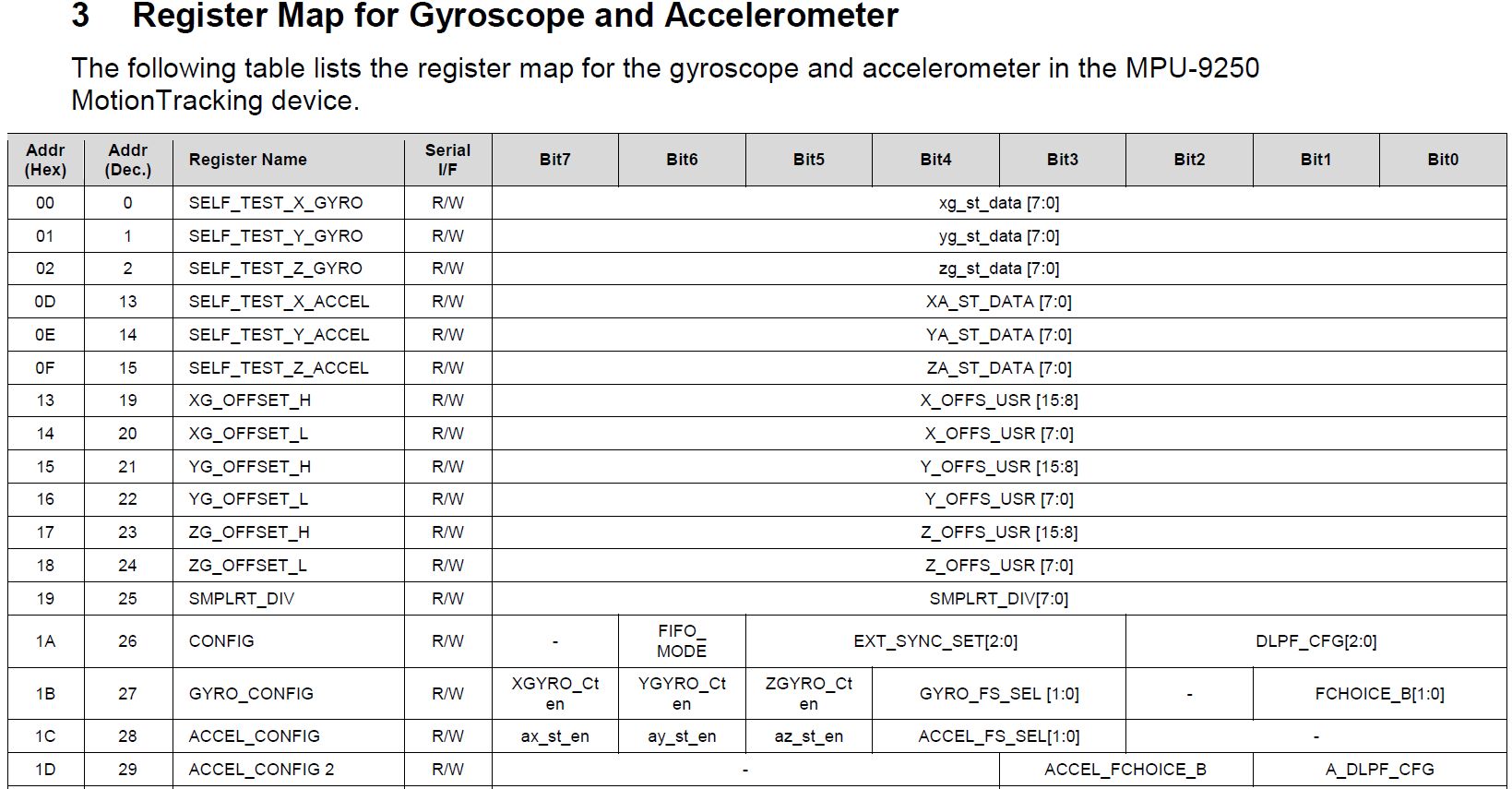
Omitiendo los detalles técnicos de la configuración, se puede decir lo siguiente. En este sensor, se realiza un filtrado personalizable de lecturas no solo de acelerómetros, giroscopios, sino también del sensor de temperatura. Para cada uno, hay un total de 7 a 10 modos, caracterizados por conceptos como Ancho de banda en Hz, retraso en ms, frecuencia de muestreo (Fs) en kHz.

La columna "Densidad de ruido" en

m u g / r t H z = m u g / s q r t H z

$\ mu g / rtHz = \ mu g / \ sqrt {Hz}$ , y la columna "Ancho de banda" se complementó con el valor "3dB".

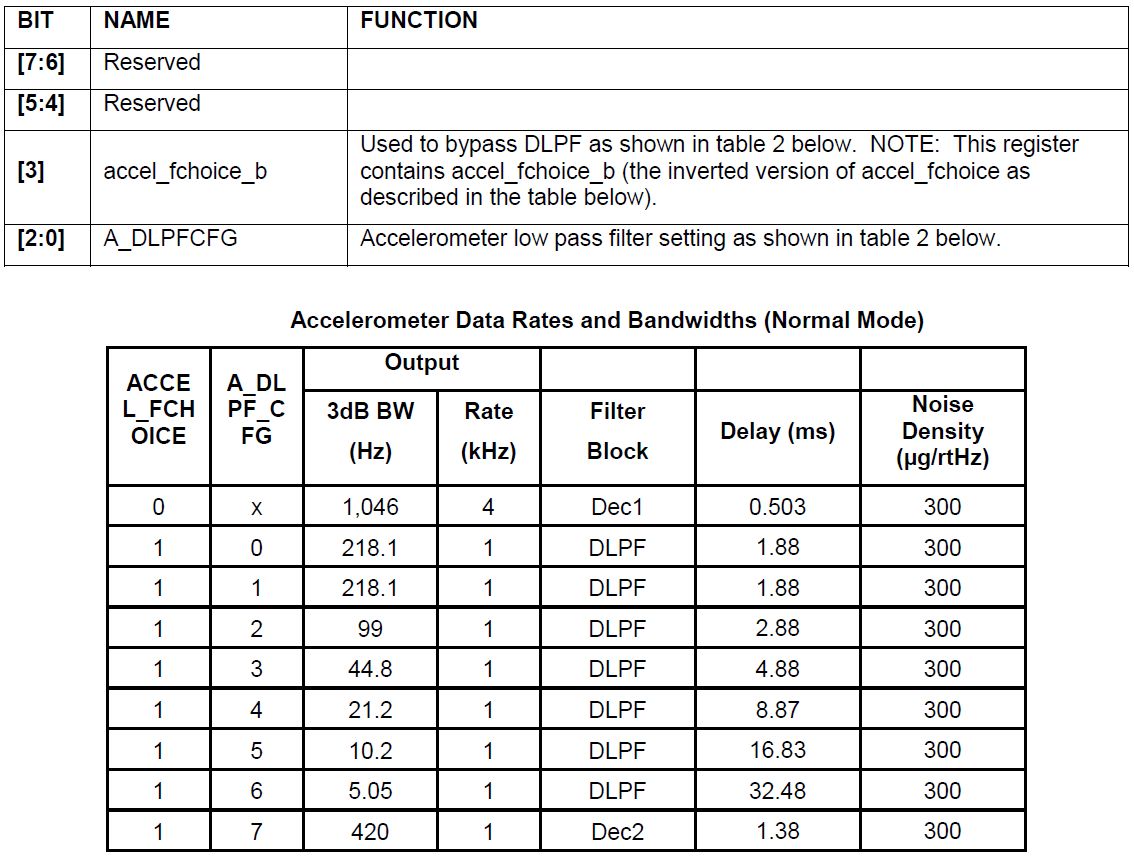
No es más fácil, así que vayamos directamente a la lista.

Legado de la antigua roma

Tasa de muestreo + diezmado

$\ Delta \ Sigma$ ADC = velocidad de datos de salida digital (ODR)

Con la frecuencia de muestreo (es la frecuencia de muestreo), todo está claro: este es el número de puntos de una señal continua en el tiempo tomada por segundo durante su muestreo por el ADC. Medido en hercios.

F s = f r a c 1 d e l t a t

$Fs = \ frac {1} {\ delta t}$

Para obtener un valor cercano a la amplitud máxima de la señal, es importante tomar una frecuencia de muestreo de al menos 10 veces la frecuencia de la señal útil. El MPU-9250 ofrece tres opciones: Fs = 32kHz, 8kHz, 1kHz.

Pero esto no significa en absoluto que la señal a la salida del acelerómetro o giroscopio aparezca con el mismo período.

Si toma los mismos drones, todo depende de la lucha para reducir el consumo de energía, aumentar la velocidad de los cálculos y reducir el ruido de los datos de salida. Puede reducir la frecuencia de actualización de los datos de salida permitiendo que los algoritmos internos integren la información de entrada durante un período de tiempo. El valor RMS disminuirá, pero el ancho de banda también se reducirá (el sensor puede detectar solo aquellos procesos cuya frecuencia será inferior al 50% de la velocidad de actualización de datos).

Aquí es mejor recordar el teorema de Kotelnikov de inmediato. Ella promete que al muestrear una señal analógica, se puede evitar la pérdida de información (es decir, restaurar la señal sin distorsión) si la frecuencia de la señal útil no es más de la mitad de la frecuencia de muestreo, también llamada frecuencia de Nyquist . En la práctica, un filtro anti-aliasing clásico (un filtro de paso bajo que reduce la contribución de los componentes de frecuencia secundarios en la señal de salida a niveles insignificantes - GOST R 8.714-2010) requiere en la mayoría de los casos una diferencia de al menos 2.5 veces [Siemens].

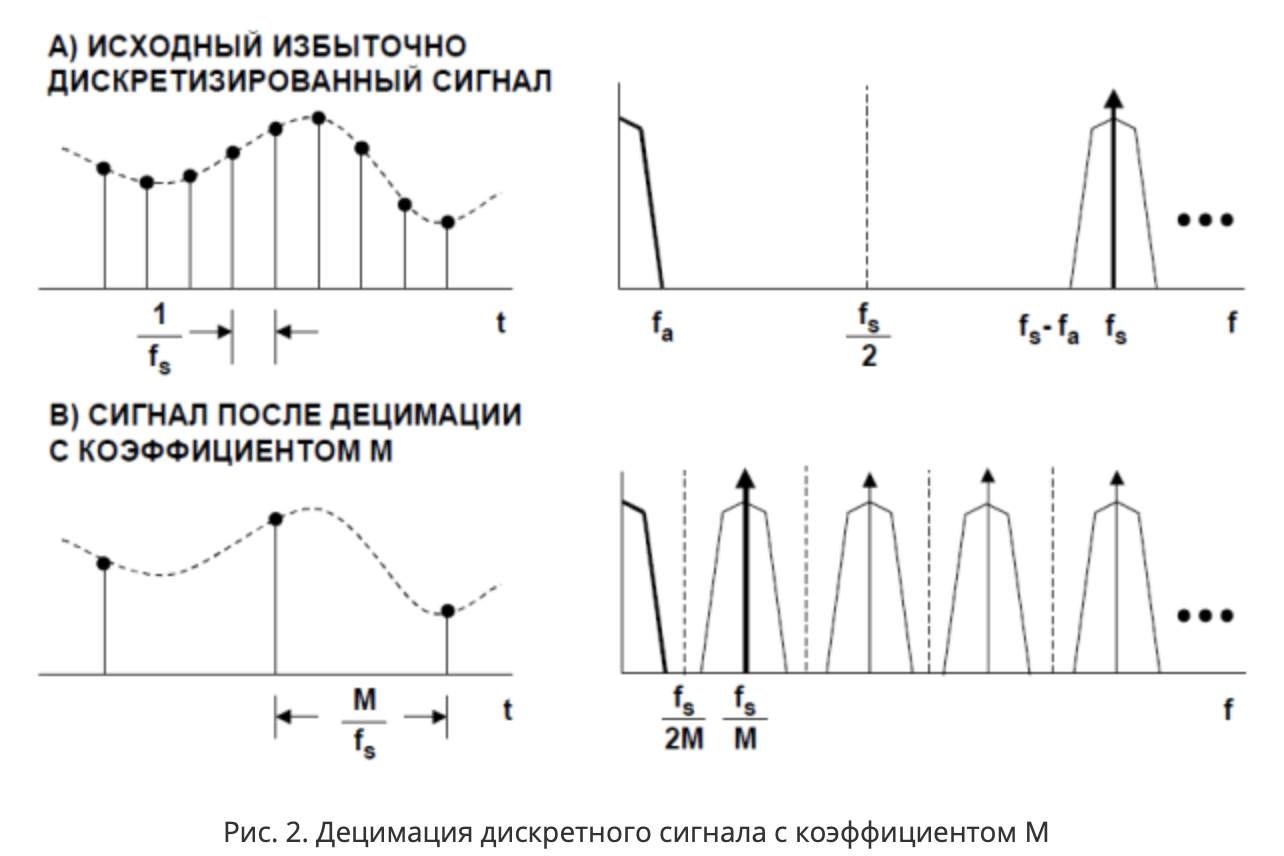
Para Fs = 32kHz, la frecuencia de Nyquist será de 16kHz. En este caso, es poco probable que una señal útil vaya más allá de la banda fa = 20Hz (pocos pueden cambiar la dirección del movimiento más de 20 veces por segundo). En total, la frecuencia de muestreo es significativamente mayor que la frecuencia requerida para almacenar la información contenida en la banda fa (40Hz, 400 veces mayor), es decir, la señal útil se sobremuestrea. La banda entre las frecuencias fa y fs-fa no contiene ninguna información útil. Puede reducir la frecuencia de muestreo (en el diagrama, esto se hizo con el coeficiente M, [7]) diluyendo la secuencia de muestras (muestras). Este proceso se llama diezmado .

De acuerdo con las especificaciones del MPU-9250, los acelerómetros están equipados con un ADC sigma-delta . Los esquemas basados en él consumen una potencia mínima. Cabe señalar que el ancho de banda de estos convertidores es muy estrecho, no excede el rango de sonido [Easyelectronics], pero para un quadrocopter estándar no es necesario más. Consisten en dos bloques:

S i g m a D e l t a

$\ Sigma \ Delta$ -modulador y filtro de paso bajo de decimación digital.

¿Por qué combinar filtro de paso bajo y diezmado?

Extracto honesto de Wiki:

Si la señal fuente no contiene frecuencias más altas que la frecuencia Nyquist de la señal diezmada, entonces la forma del espectro de la señal recibida (diezmada) coincide con la parte de baja frecuencia del espectro de la señal original. La frecuencia de muestreo correspondiente a la nueva secuencia de muestreo es N veces menor que la frecuencia de muestreo de la señal original.
Si la señal original contiene frecuencias más altas que la frecuencia de Nyquist de la señal diezmada, entonces la decimación resultará en alias (superposición de espectros).

Por lo tanto, para preservar el espectro, es necesario, antes del diezmado, eliminar de la señal original las frecuencias que son más altas que la frecuencia Nyquist de la señal diezmada. La especificación MPU-9250 no contiene mucha información sobre las características de DLPF, pero se pueden encontrar investigaciones de entusiastas [9].

Ancho de banda, es respuesta de frecuencia (respuesta de frecuencia)

El rango de frecuencia en el que el sensor detecta movimiento y proporciona una señal de salida válida. En algunas especificaciones, se da la respuesta de frecuencia del sensor: la dependencia de la salida eléctrica del acelerómetro de las tensiones mecánicas externas con una amplitud fija pero diferentes frecuencias. Dentro del ancho de banda, la desigualdad de la respuesta de frecuencia no excede un valor dado. En el caso de utilizar un filtro digital de paso bajo, la elección de la banda de paso solo le permite cambiar la frecuencia de corte, afectando inevitablemente la velocidad de respuesta del sensor a los cambios de posición en el espacio. La frecuencia de corte debe ser inferior a la mitad de la velocidad de datos de salida digital (ODR), también llamada frecuencia de Nyquist.

Para los acelerómetros MPU-9250, los límites del ancho de banda se determinan de modo que dentro del rango la densidad espectral de la señal difiera del pico (a una frecuencia de 0 Hz) no más de -3 dB. Este nivel corresponde aproximadamente a una caída a la mitad de la densidad espectral (o 70,7% de la amplitud espectral máxima). Permítanme recordarles, para las cantidades de energía (potencia, energía, densidad de energía) proporcionales a los cuadrados de la intensidad de campo, expresados en decibelios, la relación

D_{P} = 10 l g P_{2} o v e r P_{1}

$D_P = 10 \ lg {P_2 \ over {P_1}}$

.
En pocas palabras: las señales que pasan a través del filtro de paso bajo son menos ruidosas, tienen una mejor resolución, pero menos ancho de banda. Por lo tanto, no tiene sentido especificar la resolución en la especificación sin referencia al ancho de banda.

Volver a la resolución

En la especificación para el MPU-9250, básicamente no hay información sobre la resolución, para el BMI088 bajo el nombre "Resolución" se presentan la resolución digital (LSB) y la sensibilidad ":

La resolución para cada ancho de banda se puede estimar por el ruido máximo.

R u i d o_{p k - p k} = R u i d o t o t a l_{R M S} v e c e s C r e s t F a c t o r = R u i d o t o t a l_{R M S} v e c e s 4.

$Ruido_ {pk-pk} = Ruido total_ {RMS} \ veces CrestFactor = Ruido total_ {RMS} \ veces 4.$ El valor cuadrático medio del ruido en la salida está relacionado con la densidad espectral especificada en la especificación (o más bien, la raíz del mismo) y el ancho de banda de ruido equivalente (ancho de banda de ruido equivalente, ENBW): la banda de paso de un sistema equivalente que tiene una respuesta de frecuencia rectangular y el mismo valor en la frecuencia cero que el sistema original y la dispersión en la salida, cuando se expone a las entradas de los sistemas de ruido blanco):

N_{R M S} = P S D t i m e s s q r t E N B W

$N_ {RMS} = PSD \ times \ sqrt {ENBW}$

Y el ancho de banda de ruido está conectado con la banda 3dB por coeficientes correspondientes al orden del filtro de paso bajo:

E N B W = 1.57 c d o t f_{3 d B} t e x t r m p a r a e l p r i m e r p e d i d o

$ENBW = 1.57 \ cdot f_ {3dB} \ textrm {para el primer pedido}$

E N B W = 1.11 c d o t f_{3 d B} t e x t r m p a r a e l s e g u n d o o r d e n

$ENBW = 1.11 \ cdot f_ {3dB} \ textrm {para el segundo orden}$

E N B W = 1.05 c d o t f_{3 d B} t e x t r m p a r a e l t e r c e r o r d e n

$ENBW = 1.05 \ cdot f_ {3dB} \ textrm {para el tercer orden}$

E N B W = 1.025 c d o t f_{3 d B} t e x t r m p a r a c u a r t o o r d e n

$ENBW = 1.025 \ cdot f_ {3dB} \ textrm {para cuarto orden}$

A juzgar por el estudio en [MPU9250_DLPF], nuestra elección es 1.57. El valor eficaz obtenido tiene en cuenta la contribución del ruido blanco (no hay ruido de cuantificación o ruido mecánico allí). Por ejemplo, para el acelerómetro, el valor calculado para

B W = 99 H z, P S D = 300 m u g / s q r t H z

$BW = 99Hz, PSD = 300 \ mu g / \ sqrt {Hz}$ resulta

N_{R M S} = 4 m g

$N_ {RMS} = 4mg$ . En este caso, la especificación contiene el ruido rms total

R u i d o R M S t o t a l = 8 m g .

$Ruido RMS total = 8mg.$ La discrepancia es significativa. Desafortunadamente, se indica solo para una banda, y para el acelerómetro BMI088, solo se indica PSD en la especificación. Entonces usaremos lo que es. Tome el factor cruzado 4. Ahora el más interesante. Actitud

F S / R u i d o_{p k - p k}

$FS / Ruido_ {pk-pk}$ dará un orden aproximado de bits efectivos en este rango de medición, que es decentemente menor que la resolución de 16 bits del ADC.

MPU-9250			IMC088
Giroscopio
$\ small N ^ {Total} _ {RMS} = 0.1 ^ {\ circ} / s (BW = 92Hz)$			$\ small N_ {RMS} = 0.1 ^ {\ circ} / s (BW = 47Hz)$
$\ small PSD = 0.01 ^ {\ circ} / s / \ sqrt {Hz}$			$\ small PSD = 0.014 ^ {\ circ} / s / \ sqrt {Hz}$
$\ pequeño BW, Hz$	$\ small N_ {RMS}, ^ {\ circ} / s-rms$	$\ small N_ {PP}, ^ {\ circ} / s$	$\ pequeño BW, Hz$	$\ small N_ {RMS}, ^ {\ circ} / s$	$\ small N_ {PP}, ^ {\ circ} / s$
			523	0,41	1.6
250	0.2 0.2	0.8	230	0.27	1.1
184	0,17	0,69	116	0,19	0,76
92	0,12	0,49	64	0,14	0,57
41	0,08	0,32	47	0,12	0,49
20	0,06	0.23	32	0.1	0.4 0.4
10	0,04	0,16	23	0,09	0,34
5 5	0,03	0,11	12	0,06	0.25
Acelerómetro
$\ small N ^ {Total} _ {RMS} = 8mg \ textrm {(BW = 99Hz)}$			$\ small PSD_ {XY} = 160 \ mu g / \ sqrt {Hz}$
$\ small PSD = 300 \ mu g / \ sqrt {Hz} \ textrm {(Gyro off)}$			$\ small PSD_Z = 190 \ mu g / \ sqrt {Hz} (g_ {FS3g}, \ textrm {Modo normal})$
$\ pequeño BW, Hz$	$\ small N_ {RMS}, mg$	$\ small N_ {PP}, mg$	$\ pequeño BW, Hz$	$\ small N_ {RMS_XY}, mg$	$\ small N_ {PP_XY}, mg$
218,1	5.6	22	280	3.4	14
99	3.8	15	145	2,4	10
44,8	2.5	10	80	1,8	7 7
21,2	1.7	7 7	40	1.3	5 5
10,2	1,2	4.9	20	0.9	4 4
5.05	0.9	3.4	10	0.6	2.6
420	7.8	31	5 5	0.5 0.5	1,8
1046	12,3	49

Retraso (ms), o de dónde viene el retraso

Debido a la necesidad de almacenar variables en el búfer interno para dividir la señal por el filtro a diferentes frecuencias

Total Cuanto más baja es la frecuencia de corte del filtro, menos ruido hay en la señal. Pero aquí debemos tener cuidado, porque al mismo tiempo crece el retraso. Además, puede omitir la señal útil [8].

MPU-9250		IMC088
Giroscopio, 16 bit
Rango (FS) $^ {\ circ} / s$ (dps)	Resolución, bit (BW = 92Hz)	Rango (FS) $^ {\ circ} / s$ (dps)	Resolución, bit (BW = 64Hz)
		$\ pm 125$	8
$\ pm 250$	9 9	$\ pm 250$	9 9
$\ pm 500$	10	$\ pm 500$	10
$\ pm 1000$	11	$\ pm 1000$	11
$\ pm 2000$	12	$\ pm 2000$	12
Acelerómetro
Rango (FS), g	Resolución, bit $(N_ {PP} = 32mg)$	Rango (FS), g	Resolución (X, Y), bit $(N_ {PP} ^ XY = 14mg)$
$\ pm 2$	6 6	$\ pm 3$	8
$\ pm 4$	7 7	$\ pm 6$	9 9
$\ pm 8$	8	$\ pm 12$	10
$\ pm 16$	9 9	$\ pm 24$	11

Y estos son solo los parámetros más básicos.

¿De dónde vino eso?

El documento más divertido de Freescale Semiconductor es "¿Cuántos bits son suficientes?"
[EE] - "Resolución versus precisión versus sensibilidad cortando la confusión"
[Tiempo de electrónica] - "Sensores de movimiento MEMS de STMicroelectronics: acelerómetros y giroscopios"
[LSB] - “Un bit menos significativo ADC y DAC (LSB)”
[Computación de medición] - “Sugerencia técnica: precisión, precisión, resolución y sensibilidad”
[KIT] - "Acelerómetros de dispositivos analógicos - Dispositivo y aplicación"
[Easyelectronics] - "Sigma-Delta ADC"
[Radiolotsman] - "Magnetómetros: principio de funcionamiento, compensación de errores"
[SO] - "Medición de ruido"
[Mide] - "Especificaciones del acelerómetro: descifrar la hoja de datos de un acelerómetro"
[CiberLeninka] - Filtro ADC Delta-Sigma
[SciEd] - "Características de la implementación del filtrado digital con un cambio en la frecuencia de muestreo"
[MPU6050] - "Uso del DLPF del MPU6050"
[MPU9250_DLPF] - Investigación de trabajo MPU9250 Gyro Noise DLPF
Comprensión de las especificaciones de resolución del sensor
Procesamiento de señal digital de Siemens
Sensores de movimiento MEMS de STMicroelectronics
[TMWorld] - "Evaluación de unidades de medida de inercia"
[Sklyar] - Sklyar B. Comunicación digital. Fundamentos teóricos y aplicación práctica.

Acelerómetros y giroscopios MEMS: comprensión de las especificaciones