Latencia de aprendizaje: teoría de colas

El tema de la latencia en el tiempo se vuelve interesante en diferentes sistemas en Yandex y no solo. Esto sucede cuando aparecen garantías de servicio en estos sistemas. Obviamente, el hecho es que es importante no solo prometer alguna oportunidad a los usuarios, sino también garantizar su recepción con un tiempo de respuesta razonable. La "razonabilidad" del tiempo de respuesta, por supuesto, varía mucho para los diferentes sistemas, pero los principios básicos por los cuales se manifiesta la latencia en todos los sistemas son comunes, y pueden considerarse de forma aislada de los detalles.

Mi nombre es Sergey Trifonov, trabajo en el equipo de Reducción de mapas en tiempo real en Yandex. Estamos desarrollando una plataforma para el procesamiento de flujo de datos en tiempo real con tiempos de respuesta de segundos y segundos. La plataforma está disponible para usuarios internos y les permite ejecutar código de aplicación en flujos de datos entrantes constantemente. Trataré de dar una breve descripción de los conceptos básicos de la humanidad sobre el tema del análisis de latencia en los últimos ciento diez años, y ahora trataremos de comprender qué se puede aprender exactamente sobre la latencia utilizando la teoría de la cola.

El fenómeno de la latencia comenzó a investigarse sistemáticamente, hasta donde yo sé, en relación con el advenimiento de los sistemas de colas: redes de comunicación telefónica. La teoría de las colas comenzó con el trabajo de A.K. Erlang en 1909, en el que demostró que la distribución de Poisson es aplicable al tráfico telefónico aleatorio. Erlang desarrolló una teoría que se ha utilizado durante décadas para diseñar redes telefónicas. La teoría nos permite determinar la probabilidad de una denegación de servicio. Para las redes telefónicas con canales con conmutación de circuitos, se produjo un error si todos los canales están ocupados y no se puede realizar la llamada. La probabilidad de este evento tuvo que ser controlada. Quería tener una garantía de que, por ejemplo, el 95% de todas las llamadas serían atendidas. Las fórmulas de Erlang permiten determinar cuántos servidores se necesitan para cumplir con esta garantía si se conoce la duración y la cantidad de llamadas. De hecho, esta tarea se trata solo de garantías de calidad, y hoy la gente todavía resuelve problemas similares. Pero los sistemas se han vuelto mucho más complejos. El principal problema de la teoría de colas es que en la mayoría de las instituciones no se enseña, y pocas personas entienden la pregunta fuera de la cola M / M / 1 habitual (ver la notación a continuación ), pero es bien sabido que la vida es mucho más complicada que este sistema. Por lo tanto, propongo, sin pasar por M / M / 1, ir inmediatamente a lo más interesante.

Valores medios

Si no intenta obtener un conocimiento completo sobre la distribución de probabilidad en el sistema, pero se enfoca en preguntas más simples, puede obtener resultados interesantes y útiles. El más famoso de ellos es, por supuesto, el teorema de Little . Es aplicable a un sistema con cualquier flujo de entrada, dispositivo interno de cualquier complejidad y un programador arbitrario en su interior. El único requisito es que el sistema debe ser estable: deben existir tiempos de respuesta promedio y longitudes de cola, luego están conectados por una expresión simple

$$

$$L = \ lambda W$$

donde $$$L$ - el número de tiempo promedio de solicitudes en la parte considerada del sistema [pcs], $$$W$ - el tiempo promedio durante el cual las solicitudes pasan por esta parte del sistema [s], $$$\ lambda$ - la velocidad de recepción de solicitudes al sistema [pcs / s]. La fortaleza del teorema es que puede aplicarse a cualquier parte del sistema: cola, ejecutor, cola + ejecutor o toda la red. A menudo, este teorema se usa aproximadamente de esta manera: "la corriente de 1 Gbit / s se está vertiendo hacia nosotros, y medimos el tiempo de respuesta promedio, y es de 10 ms, por lo tanto, en promedio tenemos 1.25 MB en vuelo". Entonces, este cálculo no es cierto. Más precisamente, es cierto solo si todas las solicitudes tienen el mismo tamaño en bytes. El teorema de Little cuenta las consultas en piezas, no en bytes.

Cómo usar el teorema de Little

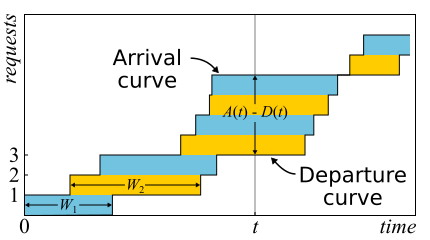
En matemáticas, a menudo es necesario estudiar evidencia para obtener una visión real. Este es solo el caso. El teorema de Little es tan bueno que doy un bosquejo de la prueba aquí. El tráfico entrante es descrito por la función $$$A (t)$ - la cantidad de solicitudes que se registraron en el momento $$$t$ . De manera similar $$$D (t)$ - el número de solicitudes que están cerradas en el momento $$$t$ . El momento de entrada (salida) de la solicitud se considera el momento de recepción (transmisión) de su último byte. Los límites del sistema están determinados solo por estos instantes de tiempo; por lo tanto, el teorema es ampliamente aplicable. Si dibuja gráficos de estas funciones en los mismos ejes, es fácil ver que $$$A (t) - D (t)$ Es el número de solicitudes en el sistema en el momento t, y $$$W_n$ - tiempo de respuesta de la enésima solicitud.

El teorema se probó formalmente solo en 1961, aunque la relación en sí se conocía mucho antes.

De hecho, si las solicitudes se pueden reordenar dentro del sistema, entonces todo es un poco más complicado, por lo que, por simplicidad, asumiremos que esto no sucede. Aunque el teorema también es cierto en este caso. Ahora calculemos el área entre las gráficas. Hay dos formas de hacer esto. En primer lugar, según las columnas, como suelen pensar las integrales. En este caso, resulta que el integrando es el tamaño de la cola en pedazos. En segundo lugar, línea por línea, simplemente sumando la latencia de todas las solicitudes. Está claro que ambos cálculos dan la misma área, por lo tanto son iguales. Si ambas partes de esta igualdad se dividen por el tiempo Δt, para el cual calculamos el área, a la izquierda tendremos la longitud promedio de la cola $$$L$ (por definición del promedio). A la derecha es un poco más complicado. Necesitamos agregar otro número de solicitudes N al numerador y al denominador, luego tendremos éxito

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

Si consideramos Δt suficientemente grande o un período de empleo, entonces las preguntas en los bordes se eliminan y el teorema puede considerarse probado.

Es importante decir que en la prueba no utilizamos ninguna distribución de probabilidades. De hecho, el teorema de Little es una ley determinista. Dichas leyes se llaman en la teoría de colas del derecho operacional. Se pueden aplicar a cualquier parte del sistema y a cualquier distribución de varias variables aleatorias. Estas leyes forman un constructor que puede usarse con éxito para analizar valores promedio en redes. La desventaja es que todos se aplican solo a promedios y no proporcionan ningún conocimiento sobre las distribuciones.

Volviendo a la pregunta de por qué el teorema de Little no se puede aplicar a bytes, supongamos que $$$A (t)$ y $$$D (t)$ ahora se miden no en piezas, sino en bytes. Luego, llevando a cabo un argumento similar, obtenemos en su lugar $$$W$ Lo extraño es el área dividida por el número total de bytes. Todavía son segundos, pero es una latencia promedio ponderada donde las solicitudes más grandes obtienen más peso. Este valor se puede llamar la latencia promedio del byte, que, en general, es lógico, ya que reemplazamos las piezas con bytes, pero no la latencia de la solicitud.

El teorema de Little dice que con un cierto flujo de solicitudes, el tiempo de respuesta y el número de solicitudes en el sistema son proporcionales. Si todas las solicitudes se ven iguales, entonces el tiempo de respuesta promedio no se puede reducir sin aumentar la potencia. Si conocemos de antemano el tamaño de las consultas, podemos intentar reordenarlas dentro para reducir el área entre $$$A (t)$ y $$$D (t)$ y, por lo tanto, el tiempo promedio de respuesta del sistema. Continuando con esta idea, podemos demostrar que los algoritmos de Tiempo de procesamiento más corto y Tiempo de procesamiento restante más corto brindan un tiempo de respuesta promedio mínimo para un servidor sin la posibilidad de desplazarse con él, respectivamente. Pero hay un efecto secundario: las solicitudes grandes no pueden procesarse indefinidamente. El fenómeno se llama "inanición" y está estrechamente relacionado con el concepto de equidad de planificación, que se puede aprender de una publicación de programación anterior : mitos y realidad .

Hay otra trampa común asociada con la comprensión de la ley de Little. Hay un servidor de subproceso único que atiende las solicitudes de los usuarios. Supongamos que de alguna manera medimos L - el número promedio de solicitudes en la cola para este servidor, y S - el tiempo promedio que el servidor atendió una solicitud. Ahora considere una nueva solicitud entrante. En promedio, ve a L consultas por delante de él. Servir a cada uno de ellos lleva un promedio de S segundos. Resulta que el tiempo de espera promedio $$$W = L S$ . Pero por el teorema resulta que $$$W = L / \ lambda$ . Si equiparamos las expresiones, entonces vemos las tonterías: $$$S = 1 / \ lambda$ . ¿Qué hay de malo en este razonamiento?

1. Lo primero que llama la atención: el tiempo de respuesta según el teorema no depende de S. De hecho, por supuesto que sí. Es solo que la longitud promedio de la cola ya tiene esto en cuenta: cuanto más rápido sea el servidor, menor será la longitud de la cola y menor el tiempo de respuesta.
2. Consideramos un sistema en el que las colas no se acumulan para siempre, sino que se restablecen regularmente. Esto significa que la utilización del servidor es inferior al 100% y omitimos todas las solicitudes entrantes, y a la misma velocidad promedio con la que llegaron estas solicitudes, lo que significa que, en promedio, no toma S segundos procesar una sola solicitud, sino más $$$1 / \ lambda$ segundos, simplemente porque a veces no procesamos ninguna solicitud. El hecho es que en cualquier sistema abierto estable sin pérdida, el rendimiento no depende de la velocidad de los servidores, sino que está determinado solo por el flujo de entrada.
3. La suposición de que una solicitud entrante ve en el sistema un número promedio de solicitudes de tiempo no siempre es cierta. Contraejemplo: las solicitudes entrantes llegan periódicamente, y logramos procesar cada solicitud antes de que llegue la siguiente. Una imagen típica para sistemas en tiempo real. Una solicitud entrante siempre ve cero solicitudes en el sistema, pero en promedio el sistema obviamente tiene más de cero solicitudes. Si las solicitudes llegan en momentos completamente aleatorios, entonces realmente "ven el número promedio de solicitudes" .
   
   
   
4. No tomamos en cuenta que con una cierta probabilidad ya puede haber una solicitud en el servidor que necesita ser "extendida". En el caso general, el tiempo promedio de "servicio posterior" difiere del tiempo inicial de servicio y, a veces, paradójicamente , puede ser mucho más largo. Volveremos a este tema al final cuando discutamos sobre microbursts, estad atentos.

Entonces, el teorema de Little se puede aplicar a sistemas grandes y pequeños, a colas, a servidores y a subprocesos de procesamiento individuales. Pero en todos estos casos, las solicitudes generalmente se clasifican de una forma u otra. Solicitudes de diferentes usuarios, solicitudes de diferentes prioridades, solicitudes provenientes de diferentes ubicaciones o solicitudes de diferentes tipos. En este caso, la información agregada por clases no es interesante. Sí, el número promedio de solicitudes mixtas y el tiempo promedio de respuesta para todos ellos son nuevamente proporcionales. Pero, ¿qué pasa si queremos saber el tiempo de respuesta promedio para una determinada clase de solicitudes? Sorprendentemente, el teorema de Little se puede aplicar a una clase específica de consultas. En este caso, debe tomar como $$$\ lambda$ La velocidad a la que solicita esta clase, no todas. Como un $$$L$ y $$$W$ - valores medios del número y el tiempo de residencia de las solicitudes de esta clase en la parte investigada del sistema.

Sistemas abiertos y cerrados.

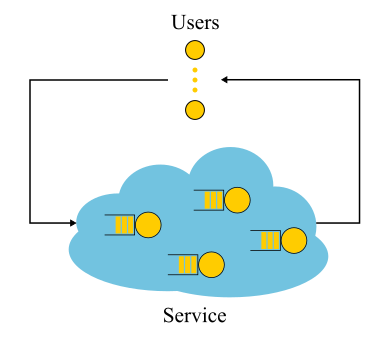
Vale la pena señalar que para los sistemas cerrados, la línea de razonamiento "equivocada" conduce a la conclusión $$$S = 1 / \ lambda$ Resulta ser cierto. Los sistemas cerrados son aquellos en los que las solicitudes no provienen del exterior y no salen, sino que circulan dentro. O, de lo contrario, los sistemas de retroalimentación: tan pronto como la solicitud abandona el sistema, una nueva solicitud toma su lugar. Estos sistemas también son importantes porque cualquier sistema abierto puede considerarse inmerso en un sistema cerrado. Por ejemplo, puede considerar el sitio como un sistema abierto, en el que las solicitudes se vierten, procesan y retiran constantemente, o, por el contrario, como un sistema cerrado junto con toda la audiencia del sitio. Luego, por lo general, dicen que el número de usuarios es fijo y esperan una respuesta a la solicitud o "piensan": recibieron su página y aún no han hecho clic en el enlace. En el caso de que el tiempo de reflexión sea siempre cero, el sistema también se llama sistema por lotes.

La ley de Little para sistemas cerrados es válida si la velocidad de las llegadas externas $$$\ lambda$ (no están en un sistema cerrado) reemplace con el ancho de banda del sistema. Si envolvemos el servidor de subproceso único mencionado anteriormente en un sistema por lotes, obtenemos $$$S = 1 / \ lambda$ y 100% de reciclaje. A menudo, una mirada al sistema da resultados inesperados. En los años 90, fue precisamente esta visión de Internet junto con los usuarios como un sistema único lo que impulsó el estudio de distribuciones distintas a la exponencial. Discutiremos las distribuciones más a fondo, pero aquí notamos que en ese momento casi todo y en todas partes se consideraba exponencial, y esto incluso se encontró alguna justificación, y no solo una excusa en el espíritu de "de lo contrario demasiado complicado". Sin embargo, resultó que no todas las distribuciones prácticamente importantes tienen colas igualmente largas, y se puede probar el conocimiento de las colas de distribución. Pero por ahora, volvamos a los valores promedio.

Efectos relativistas

Supongamos que tenemos un sistema abierto: una red compleja o un servidor simple de un solo subproceso, no importa. ¿Qué cambiará si duplicamos la llegada de solicitudes y aceleramos su procesamiento a la mitad, por ejemplo, duplicando la capacidad de todos los componentes del sistema? ¿Cómo cambiarán la utilización, el rendimiento, el número promedio de solicitudes en el sistema y el tiempo promedio de respuesta? Para un servidor de un solo subproceso, puede intentar tomar las fórmulas, aplicarlas "en la frente" y obtener los resultados, pero ¿qué hacer con una red arbitraria? La solución intuitiva es la siguiente. Supongamos que el tiempo se duplica, luego, en nuestro "sistema de referencia acelerado", la velocidad de los servidores y el flujo de solicitudes no parecen cambiar; en consecuencia, todos los parámetros en tiempo acelerado tienen los mismos valores que antes. En otras palabras, la aceleración de todas las "partes móviles" de cualquier sistema es equivalente a la aceleración del reloj. Ahora convertiremos los valores a un sistema con un tiempo normal. Las cantidades adimensionales (utilización y número promedio de solicitudes) no cambiarán. Los valores cuya dimensión incluye factores de tiempo de primer grado varían proporcionalmente. El rendimiento de [peticiones / s] se duplicará, y los tiempos de respuesta y espera [s] se reducirán a la mitad.

Este resultado se puede interpretar de dos maneras:

1. Un sistema acelerado por k veces puede digerir el flujo de tareas k veces más, y con un tiempo de respuesta promedio k veces menos.
2. Podemos decir que el poder no cambió, pero simplemente el tamaño de las tareas disminuyó k veces. Resulta que estamos enviando la misma carga al sistema, pero aserrada en piezas más pequeñas. Y ... ¡oh, un milagro! ¡El tiempo de respuesta promedio se reduce!

Una vez más, noto que esto es cierto para una amplia clase de sistemas, y no solo para un servidor simple. Desde un punto de vista práctico, solo hay dos problemas:

1. No todas las partes del sistema se pueden acelerar fácilmente. No podemos influir en algunos en absoluto. Por ejemplo, la velocidad de la luz.
2. No todas las tareas se pueden dividir infinitamente en pequeñas y pequeñas, ya que no se ha aprendido a transferir información en porciones de menos de un bit.

Considere el pasaje al límite. Supongamos, en el mismo sistema abierto, la interpretación No. 2. Dividimos cada solicitud entrante por la mitad. El tiempo de respuesta también se divide a la mitad. Repita la división muchas veces. Y ni siquiera necesitamos cambiar nada en el sistema. Resulta que puede hacer que el tiempo de respuesta sea arbitrariamente pequeño simplemente cortando las solicitudes entrantes en un número suficientemente grande de partes. En el límite, podemos decir que en lugar de consultas obtenemos un "fluido de consulta", que filtramos por nuestros servidores. Este es el llamado modelo fluido, una herramienta muy conveniente para el análisis simplificado. Pero, ¿por qué el tiempo de respuesta es cero? ¿Qué salió mal? ¿Dónde no consideramos la latencia? Resulta que no tomamos en cuenta solo la velocidad de la luz, no se puede duplicar. El tiempo de propagación en el canal de red no se puede cambiar, solo puede soportarlo. De hecho, la transmisión a través de una red incluye dos componentes: tiempo de transmisión y tiempo de propagación. El primero puede acelerarse aumentando la potencia (ancho del canal) o reduciendo el tamaño de los paquetes, y el segundo es muy difícil de influir. En nuestro "modelo líquido" simplemente no había depósitos para acumular líquidos: canales de red con tiempos de propagación constantes y distintos de cero. Por cierto, si los agregamos a nuestro "modelo líquido", la latencia estará determinada por la suma de los tiempos de propagación, y las colas en los nodos aún estarán vacías. Las colas dependen solo del tamaño de los paquetes y la variabilidad (ráfaga de lectura) del flujo de entrada.

De esto se deduce que cuando se trata de latencia, no se puede hacer el cálculo de los flujos, e incluso el reciclaje de dispositivos no resuelve todo. Es necesario tener en cuenta el tamaño de las solicitudes y no olvidar el tiempo de distribución, que a menudo se ignora en la teoría de colas, aunque agregarlo a los cálculos no es nada difícil.

Distribuciones

¿Cuál es la razón para hacer cola? Obviamente, el sistema no tiene suficiente capacidad y el exceso de solicitudes se está acumulando. No es cierto! Las colas también surgen en sistemas donde hay suficientes recursos. Si no hay suficiente capacidad, entonces el sistema, como dicen los teóricos, no es estable. Hay dos razones principales para hacer cola: la irregularidad de las solicitudes y la variabilidad del tamaño de las solicitudes. Ya hemos examinado un ejemplo en el que se han eliminado estas dos razones: un sistema en tiempo real donde las solicitudes del mismo tamaño llegan estrictamente de forma periódica. Nunca se forma una cola. El tiempo de espera promedio en la cola es cero. , , , . , .

A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

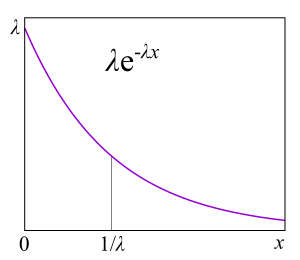
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . $$$a=1.16$ , 80/20: 20% 80% .

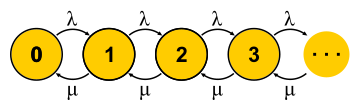
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ . , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ donde $$$\rho = \lambda / \mu$ - Esta es la utilización del servidor. El final de la historia. En el curso de la presentación, me perdí una cantidad decente de suposiciones e hice un par de sustituciones de conceptos, pero la esencia, espero, no sufrió.

Es importante entender que este enfoque solo funciona si el estado actual de la máquina determina completamente su comportamiento adicional, y la historia de cómo llegó a este estado no es importante. Para la comprensión cotidiana de una máquina de estados finitos, esto es evidente: después de todo, es una condición para eso. Pero para un proceso estocástico, se deduce de esto que todas las distribuciones deben ser exponenciales, ya que solo ellas no tienen memoria, tienen una tasa de falla constante.

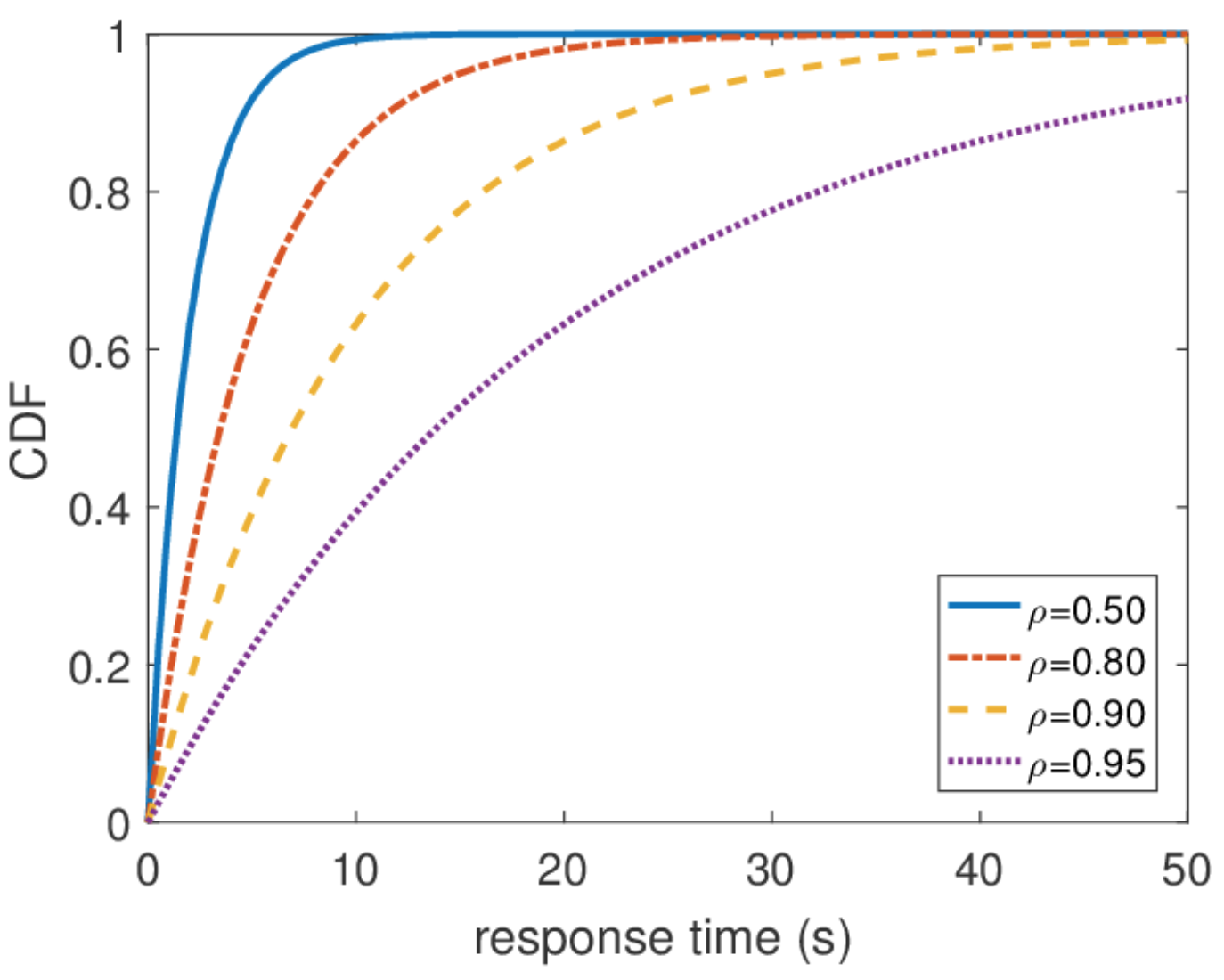
También es importante decir que toda otra información sobre el sistema es fácil de obtener si conocemos la distribución de equilibrio. El número promedio de consultas en el sistema es el promedio de esta distribución. Para averiguar el tiempo de respuesta promedio, aplicamos el teorema de Little al número de consultas. La distribución del tiempo de respuesta es un poco más difícil de encontrar, pero también en algunas acciones puede descubrir que $$$\ mathbf {P} \ {respuesta \ _time> t \} = e ^ {- (\ mu- \ lambda) t}$ y cual es el tiempo promedio de respuesta $$$1 / (\ mu- \ lambda)$ .

Tiempo de respuesta ilimitado

A partir de esta distribución, puede encontrar cualquier percentil del tiempo de respuesta, y resulta que el centésimo percentil es igual al infinito. En otras palabras, el peor tiempo de respuesta no está limitado desde arriba. Lo cual, en general, no es sorprendente, ya que utilizamos la corriente de Poisson. Pero en la práctica, tal comportamiento nunca se puede cumplir. Obviamente, el flujo de entrada de solicitudes al servidor está limitado, al menos por el ancho del canal de red a este servidor, y la longitud de la cola está limitada por la memoria en este servidor. La corriente de Poisson, por el contrario, con probabilidad distinta de cero garantiza la aparición de explosiones arbitrariamente grandes. Por lo tanto, no recomendaría proceder del supuesto de una secuencia de entrada de Poisson al diseñar un sistema si está interesado en percentiles altos y la carga del sistema es muy alta. Es mejor usar otros modelos de tráfico, de los que hablaré en otro momento cuando hablaré sobre el cálculo de la red.

Escalado y garantías

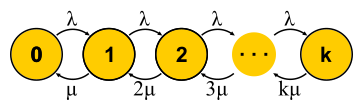
Ahora que tenemos una forma lo suficientemente poderosa de analizar sistemas, podemos intentar aplicarlo a diferentes tareas y cosechar los beneficios. Así es como se desarrolló la teoría del servicio de masas en la segunda mitad del siglo XX. Tratemos de entender lo que se logró. Para empezar, volvamos a las tareas que Erlang resolvió. Estas son las tareas M / M / k / k y M / M / k, en las que nos gustaría limitar la probabilidad de falla. Resulta que no les resulta difícil construir cadenas de Markov. La diferencia es que a medida que se agregan tareas, la probabilidad de una transición inversa aumenta, ya que las tareas comienzan a procesarse en paralelo, pero cuando el número de tareas es igual al número de servidores, se produce la saturación. Además, para M / M / k / k, la red termina, el autómata realmente resulta ser finito, y todas las solicitudes que llegan al último estado son denegadas. La probabilidad de este evento es simplemente igual a la probabilidad de que estemos en el último estado.

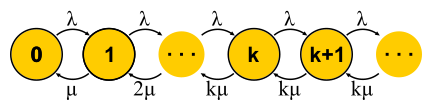
Para M / M / k, la situación es más complicada, las solicitudes se ponen en cola, aparecen nuevos estados, pero la probabilidad de una transición inversa no aumenta: todos los servidores ya están funcionando. La red se vuelve infinita, como para M / M / 1. Por cierto, si el número de solicitudes en el sistema es limitado, la cadena siempre tendrá un número finito de estados y de una forma u otra se resolverá, lo que no se puede decir sobre las cadenas sin fin. En sistemas cerrados, las cadenas son siempre finitas. Resolviendo los circuitos descritos para M / M / k / k y M / M / k, llegamos a la fórmula B y la fórmula C de Erlang , respectivamente. Son bastante voluminosos, no los daré, pero con su ayuda puede obtener un resultado interesante para el desarrollo de la intuición, que se llama regla de personal de raíz cuadrada. Supongamos que hay un sistema M / M / k con un flujo de entrada dado λ de solicitudes por segundo. Supongamos que la carga debería duplicarse para mañana. La pregunta es: ¿cómo aumentar el número de servidores para que el tiempo de respuesta sea el mismo? La cantidad de servidores debe duplicarse, ¿verdad? Resulta que no del todo. Recuerde que ya hemos visto: si acelera el tiempo (servidores e inicio de sesión) a la mitad, el tiempo de respuesta promedio disminuye a la mitad. Varios servidores lentos y uno rápido no son lo mismo, pero la potencia informática es la misma. En particular, para M / M / 1, por ejemplo, el tiempo de respuesta es inversamente proporcional al volumen de "capacidad libre" $$$\ mu - \ lambda$ y está determinado solo por este volumen. Al duplicar tanto el flujo como la potencia de procesamiento, la capacidad libre del sistema se duplica: $$$2 \ mu - 2 \ lambda$ . Puede parecer que para resolver el problema solo necesita guardar la capacidad libre, pero el tiempo de respuesta en M / M / k ya está determinado por la fórmula más compleja de Erlang. Resulta que la capacidad libre debe mantenerse en proporción a la raíz cuadrada del número de "servidores ocupados" para mantener el mismo tiempo de respuesta. Por el número de "servidores ocupados" se entiende el número total de servidores multiplicado por la utilización: este es el número mínimo de servidores necesarios para una operación estable.

Con esta regla, a veces intentan justificar cómo expandir un clúster con servidores. Pero no se haga ilusiones de que cualquier clúster es un sistema M / M / k. Por ejemplo, si tiene un equilibrador en su entrada que envía solicitudes en las colas a los servidores, esto ya no es M / M / k, ya que M / M / k implica una cola común de la que los servidores recogen las solicitudes cuando se liberan. Pero este modelo es adecuado, por ejemplo, para grupos de subprocesos con una cola FIFO común. Sin embargo, incluso en este caso, vale la pena recordar que esta regla es una aproximación para el caso cuando hay muchos hilos. De hecho, si tiene más de 10 hilos, puede asumir con seguridad que hay muchos de ellos. Bueno, no se olvide de las distribuciones exponenciales ubicuas: sin asumir la exponencialidad de todas las distribuciones, la regla tampoco funciona.

Tiempo de respuesta de la red

En última instancia, es de interés una red de M / M / k conectada al menos en una cadena, ya que hacemos sistemas distribuidos. Para estudiar redes, me gustaría tener un constructor: reglas simples y claras para conectar elementos conocidos en bloques. En la teoría del control, por ejemplo, hay funciones de transferencia que se combinan comprensiblemente con conexiones en serie o paralelas. Aquí, la secuencia de salida de cualquier nodo tiene una distribución muy complicada, con la excepción de M / M / k, que, según el conocido teorema de Burke, produce una secuencia de Poisson independiente. Esta excepción, como puede suponer, se usa principalmente.

La conexión de dos corrientes de Poisson es una corriente de Poisson. La separación probabilística de la corriente de Poisson en dos nuevamente da dos flujos de Poisson. Todo esto lleva al hecho de que todas las colas en el sistema son como independientes, y puede obtener, en un lenguaje formal, la llamada solución de forma de producto . Es decir, la distribución conjunta de las longitudes de las colas es simplemente el producto de las distribuciones de las longitudes de todas las colas, consideradas por separado; así es como se expresa la independencia en la teoría de la probabilidad. Simplemente encontramos los flujos de entrada a todos los nodos y usamos las fórmulas para cada nodo de forma independiente. Hay una serie de limitaciones:

1. Algoritmo de enrutamiento probabilístico. La solicitud atendida por el nodo selecciona la siguiente al azar con una probabilidad conocida. Esto no es tan malo como podría parecer, porque es posible usar "clases de solicitud": digamos que todas las solicitudes de Vasya llegan al servidor número 1, luego al servidor número 2 y luego salen de la red, y las solicitudes de Petya llegan al servidor número 2 , y luego, con igual probabilidad, visite el servidor número 1 o número 3 y salga. Es decir, no todas las transiciones deben ser aleatorias, algunas o incluso todas pueden tener una probabilidad del 100%.
2. Asunción de la independencia de Kleinrock. El tiempo de procesamiento de la solicitud no puede depender del historial o la clase de la solicitud, sino que solo lo determina el servidor, y cuando la solicitud pasa nuevamente por el mismo servidor, se selecciona aleatoriamente cada vez. De hecho, no hay forma de establecer el tamaño de la solicitud que se utilizaría en diferentes servidores, y el tiempo de servicio solo lo determina el propio servidor. También puede intentar evitar esta limitación. Para esto, generalmente se usa el enrutamiento probabilístico y se realiza un bucle para regresar al mismo servidor con cierta probabilidad, como si reiniciaran la solicitud. En mi opinión, este es un truco bastante extraño, porque dicha solicitud vuelve a entrar en la cola y no se realiza de inmediato, pero para algunas tareas esto no es importante.
3. Tráfico de entrada de Poisson y tiempo de servicio exponencial en todos los nodos.

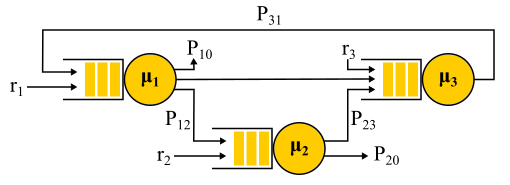
Jackson Network Ejemplo.

Vale la pena señalar que en presencia de retroalimentación, NO se obtiene una corriente de Poisson, ya que los flujos resultan ser interdependientes. En la salida del nodo de retroalimentación, también se obtiene un flujo no Poisson y, como resultado, todos los flujos se vuelven no Poisson. Sin embargo, de manera sorprendente, resulta que todos estos flujos que no son de Poisson se comportan exactamente igual que los flujos de Poisson (oh, esta teoría de probabilidad) si se cumplen las restricciones anteriores. Y luego nuevamente obtenemos una solución de forma de producto. Dichas redes se denominan redes Jackson , pueden proporcionar comentarios y, por lo tanto, múltiples visitas a cualquier servidor. Hay otras redes en las que se permiten más libertades, pero como resultado, todos los logros analíticos significativos de la teoría de colas en relación con las redes involucran corrientes de Poisson en la solución de entrada y forma de producto, que se convirtió en objeto de crítica de esta teoría y condujo en los años 90 a el desarrollo de otras teorías y el estudio de qué distribución es realmente necesaria y cómo trabajar con ellas.

Una aplicación importante de toda esta teoría de las redes Jackson es el modelado de paquetes en redes IP y redes ATM. El modelo es bastante adecuado: los tamaños de los paquetes no varían mucho y no dependen del paquete en sí, solo del ancho del canal, ya que el tiempo de servicio corresponde al momento en que se envió el paquete al canal. El tiempo de envío aleatorio, aunque suena salvaje, en realidad no tiene una gran variabilidad. Además, resulta que en una red con tiempo de servicio determinista, la latencia no puede ser mayor que en una red Jackson similar, por lo que estas redes se pueden usar de manera segura para estimar el tiempo de respuesta desde arriba.

Distribuciones no exponenciales

Todos los resultados de los que hablé estaban relacionados con distribuciones exponenciales, pero también mencioné que las distribuciones reales son diferentes. Existe la sensación de que toda esta teoría es bastante inútil. Esto no es del todo cierto. Hay una manera de integrar otras distribuciones en este aparato matemático, además, prácticamente cualquier distribución, pero nos costará algo. Con la excepción de algunos casos interesantes, se pierde la oportunidad de obtener una solución de forma explícita, se pierde la solución de la forma del producto y, con ello, el constructor: cada problema debe resolverse completamente desde cero utilizando cadenas de Markov. Para la teoría, este es un gran problema, pero en la práctica simplemente significa la aplicación de métodos numéricos y permite resolver problemas mucho más complejos y cercanos a la realidad.

Método de fase

La idea es simple. Las cadenas de Markov no nos permiten tener memoria dentro de un estado, por lo tanto, todas las transiciones deben ser aleatorias con una distribución exponencial de tiempo entre dos transiciones. Pero, ¿qué pasa si el estado se divide en varios subestados? Las transiciones entre subestados aún deben tener una distribución exponencial si queremos que toda la estructura siga siendo una cadena de Markov, y realmente queremos, porque sabemos cómo resolver esas cadenas. Los subestados a menudo se denominan fases si están organizados en serie, y el proceso de partición se denomina método de fase.

El ejemplo más simple. La solicitud se procesa en varias fases: primero, por ejemplo, leemos los datos necesarios de la base de datos, luego realizamos algunos cálculos y luego escribimos los resultados en la base de datos. Suponga que todas estas tres etapas tienen la misma distribución exponencial de tiempo. ¿Qué distribución tiene el tiempo de tránsito de las tres fases juntas? Esta es la distribución de Erlang.



Pero, ¿qué pasa si haces muchas, muchas fases idénticas cortas? En el límite, obtenemos una distribución determinista. Es decir, al construir una cadena, puede reducir la variabilidad de la distribución.

¿Es posible aumentar la variabilidad? Fácil En lugar de una cadena de fase, utilizamos categorías alternativas, eligiendo al azar una de ellas. Un ejemplo Casi todas las solicitudes se ejecutan rápidamente, pero existe una pequeña posibilidad de que llegue una gran solicitud, lo que lleva mucho tiempo. Tal distribución tendrá una tasa de falla decreciente. Cuanto más esperemos, más probable es que la solicitud caiga en la segunda categoría.



Continuando con el desarrollo del método de fases, los teóricos han descubierto que existe una clase de distribuciones con las que puede abordar con precisión una distribución arbitraria no negativa. La distribución de Coxian se construye mediante el método de fase, solo que no estamos obligados a pasar por todas las fases, después de cada fase hay alguna probabilidad de finalización.



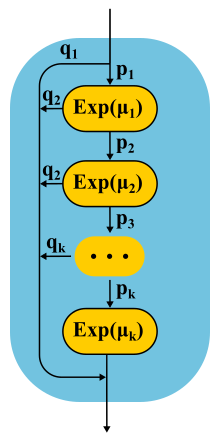
Este tipo de distribución se puede usar tanto para generar un flujo de entrada no Poisson como para crear un tiempo de servicio no exponencial. Aquí, por ejemplo, está la cadena de Markov para el sistema M / E2 / 1 con distribución Erlang por tiempo de servicio. El estado está determinado por un par de números (n, s), donde n es la longitud de la cola y s es el número de la etapa donde se encuentra el servidor: primero o segundo. Todas las combinaciones de nys son posibles. Los mensajes entrantes cambian solo n, y al finalizar las fases, se alternan y disminuyen la longitud de la cola después de la finalización de la segunda fase.

Tienes microbursts!

¿Se puede ralentizar un sistema cargado con la mitad de su capacidad? Como primer sujeto de prueba, preparamos M / G / 1. Dado: flujo de Poisson en la entrada y distribución arbitraria del tiempo de servicio. Considere la ruta de una sola solicitud a través de todo el sistema. Una solicitud entrante aleatoriamente ve en la cola frente a sí misma el número de solicitudes de tiempo promedio $$$\ mathbf {E} [N_Q]$ . El tiempo promedio de procesamiento para cada uno de ellos. $$$\ mathbf {E} [S]$ . Con una probabilidad igual a la eliminación $$$\ rho$ , hay otra solicitud en el servidor, que primero debe ser "atendida" a tiempo $$$\ mathbf {E} [S_e]$ . En resumen, obtenemos que el tiempo de espera total en la cola $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e]$ . Por el teorema de Little $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ; combinando, obtenemos:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

Es decir, el tiempo de espera en la cola está determinado por dos factores. El primero es el efecto de la utilización del servidor, y el segundo es el tiempo promedio después del servicio. Considere el segundo factor. Una solicitud que llega en algún momento $$$t$ , ve que el cuidado posterior lleva tiempo $$$S_e (t)$ .



Tiempo medio $$$\ mathbf {E} [S_e]$ determinado por el valor promedio de la función $$$S_e (t)$ , es decir, el área de triángulos dividida por el tiempo total. Está claro que podemos limitarnos a un triángulo "medio", luego $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ . Esto es bastante inesperado. Hemos recibido que el tiempo posterior al servicio está determinado no solo por el valor promedio del tiempo de servicio, sino también por su variabilidad. La explicación es simple. La probabilidad de caer en un intervalo largo $$$S$ Además, en realidad es proporcional a la duración S de este intervalo. Esto explica la famosa paradoja del tiempo de espera, o paradoja de la inspección. Pero volvamos a M / G / 1. Si combina todo lo que tenemos y lo reescribe usando variabilidad $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ obtenga la famosa fórmula Pollaczek-Khinchine :

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2} (C ^ 2_S + 1)$$

Si la prueba te aburrió, espero que complazca el resultado de su aplicación en la práctica. Ya hemos examinado los datos de tiempo de servicio en RTMR. La larga cola solo surge con gran variabilidad, y en este caso $$$C ^ 2_S = 381$ . Esto, ves, es mucho más que $$$C ^ 2_S = 1$ para distribución exponencial. En promedio, todo es súper rápido: $$$\ mathbf {E} [S] = 263.792 μs$ . Ahora suponga que RTMR está modelado por el sistema M / G / 1, y deje que el sistema no esté muy cargado, deseche $$$\ rho = 0.5$ . Sustituyendo en la fórmula, obtenemos $$$\ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263.792 μs = 50 ms$ . Debido a los microbursts, incluso un sistema tan rápido y poco utilizado puede convertirse, en promedio, en uno desagradable. ¡Durante 50 ms, puede ir al disco duro 6 veces o, si tiene suerte, incluso a un centro de datos en otro continente! Por cierto, para G / G / 1 hay una aproximación que tiene en cuenta la variabilidad del tráfico entrante: se ve exactamente igual, solo que en su lugar $$$C ^ 2_S + 1$ es la suma de ambas variedades $$$C ^ 2_S + C ^ 2_A$ . Para el caso de varios servidores, las cosas son mejores, pero el efecto de varios servidores afecta solo el primer factor. El efecto de la variabilidad sigue siendo: $$$\ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2$ .

¿Cómo son las microburst? Con respecto a los grupos de subprocesos, estas son tareas que se atienden lo suficientemente rápido como para no ser visibles en los programas de reciclaje, y lo suficientemente lentas como para crear una cola detrás de ellos y afectar el tiempo de respuesta del grupo. Desde un punto de vista teórico, estas son grandes consultas desde el final de la distribución. Supongamos que tiene un grupo de 10 subprocesos y observa el programa de reciclaje, basado en las métricas de tiempo de operación y tiempo de inactividad, que se recopilan cada 15 segundos. En primer lugar, es posible que no note que un hilo está colgando, o que los 10 hilos realizaron simultáneamente tareas grandes durante un segundo, y luego no hicieron nada durante 14 segundos. Una resolución de 15 segundos no permite ver un salto de utilización de hasta el 100% y volver al 0%, y el tiempo de respuesta sufre. , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

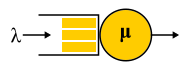
, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . Solución $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ . $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ .

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. La presentación más simple, en la medida de lo posible sin pérdida de significado, de los clásicos de la teoría que conozco en el formato de video conferencias de Robert B. Cooper. En estas conferencias, cuenta de manera muy inteligible casi todo su libro y todo lo que se requiere para comprenderlo.