El muestreo de tanques (ing. "Muestreo de yacimientos") es un algoritmo simple y eficiente para muestrear aleatoriamente un cierto número de elementos de un vector existente de tamaño grande y / o desconocido. No encontré ningún artículo sobre este algoritmo en Habré y, por lo tanto, decidí escribirlo yo mismo.
Entonces, ¿de qué estamos hablando? Seleccionar un elemento aleatorio de un vector es una tarea elemental:
La tarea de "devolver K elementos aleatorios de un vector de tamaño N" ya es más complicada. Aquí ya puede cometer un error; por ejemplo, tome los primeros elementos K (esto viola el requisito de aleatoriedad) o tome cada uno de los elementos con probabilidad K / N (esto viola el requisito de tomar exactamente K elementos). Además, es posible implementar una solución formalmente correcta, pero extremadamente ineficaz "mezclar aleatoriamente todos los elementos y tomar la K primero". Y todo se vuelve aún más interesante si agregamos la condición de que N es un número muy grande (no tenemos suficiente memoria para guardar todos los elementos N) y / o no se conoce de antemano. Por ejemplo, imagine que tenemos algún tipo de servicio externo que nos envía elementos de uno en uno. No sabemos cuántos de ellos vendrán en total, y no podemos guardarlos a todos, pero queremos tener un conjunto de K elementos seleccionados aleatoriamente de los recibidos en un momento dado.
El algoritmo de muestreo de yacimientos nos permite resolver este problema en pasos O (N) y memoria O (K). En este caso, no es necesario conocer N por adelantado, y se observará claramente la condición de muestreo aleatorio de exactamente K elementos.
Comencemos con una tarea simplificada.
Deje K = 1, es decir necesitamos seleccionar solo un elemento de todos los entrantes, pero para que cada uno de los elementos entrantes tenga la misma probabilidad de ser seleccionado. El algoritmo se sugiere a sí mismo:
Paso 1 : Asignar memoria a exactamente un elemento. Guardamos en él el primer elemento que llegó.

Hasta ahora, todo está bien: solo nos ha llegado un elemento, con una probabilidad del 100% (en este momento) de que debería seleccionarse, lo está.
Paso 2 : el segundo elemento entrante se reescribe con una probabilidad de 1/2 como el seleccionado.

Aquí, también, todo está bien: hasta ahora, solo nos han llegado dos elementos. El primero permaneció seleccionado con una probabilidad de 1/2, el segundo lo reescribió con una probabilidad de 1/2.
Paso 3 : el tercer elemento entrante con una probabilidad de 1/3 se reescribe como el seleccionado.
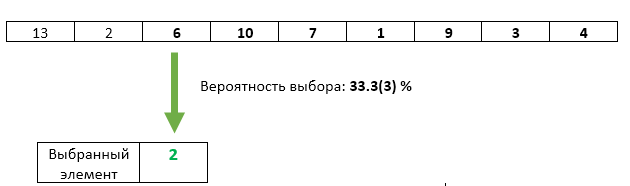
Todo está bien con el tercer elemento: su posibilidad de ser elegido es exactamente 1/3. ¿Pero de alguna manera hemos violado la igualdad de oportunidades de los elementos anteriores? No La probabilidad de que el elemento seleccionado no se sobrescriba en este paso es 1 - 1/3 = 2/3. Y dado que en el paso 2 garantizamos las mismas oportunidades para cada uno de los elementos que se seleccionarán, después del paso 3, cada uno de ellos se puede seleccionar con una probabilidad de 2/3 * 1/2 = 1/3. Exactamente la misma oportunidad que el tercer elemento.
Paso N : con una probabilidad de 1 / N, el número de elemento N se reescribe como el seleccionado. Cada uno de los artículos anteriores que llegaron tiene la misma probabilidad de 1 / N de permanecer seleccionado.
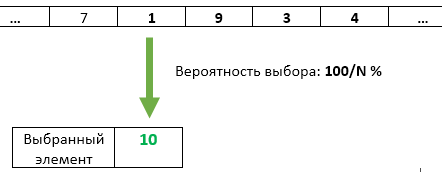
Pero era una tarea simplificada, con K = 1.
¿Cómo cambiará el algoritmo para K> 1?
Paso 1 : Asignamos memoria en K elementos. Escribimos en él los primeros elementos K llegaron.

La única forma de tomar K elementos de K elementos llegados es tomarlos todos :)
Paso N : (para cada N> K): genera un número aleatorio X de 1 a N. Si X> K, descartamos este elemento y pasamos al siguiente. Si X <= K, reescriba el elemento con el número X. Dado que el valor de X será uniformemente aleatorio en el rango de 1 a N, bajo la condición X <= K será uniformemente aleatorio en el rango de 1 a K. Por lo tanto, aseguramos la uniformidad selección de artículos regrabables.

Como puede ver, cada elemento siguiente que viene tiene cada vez menos posibilidades de ser seleccionado. Sin embargo, siempre será exactamente K / N (en cuanto a cada uno de los elementos anteriores que llegaron).
La ventaja de este algoritmo es que podemos detenernos en cualquier momento, mostrarle al usuario el vector K actual, y este será el vector de elementos aleatorios seleccionados honestamente de la secuencia de elementos que llegaron. Quizás esto le convenga al usuario, o tal vez quiera continuar procesando los valores entrantes; podemos hacerlo en cualquier momento. En este caso, como se mencionó al principio, nunca usamos más que la memoria O (K).
Ah, sí, lo olvidé por completo, la función
std :: sample , que hace exactamente lo que se describió anteriormente, finalmente se incluye en la biblioteca estándar de C ++ 17. El estándar no lo obliga a usar solo el muestreo del yacimiento, sino que lo obliga a trabajar en pasos O (N); bueno, es poco probable que los desarrolladores de su implementación en la biblioteca estándar elijan algún algoritmo que use más que memoria O (K) (y menos fallará también - El resultado debe almacenarse en algún lugar).
Materiales relacionados