Torres de hanoiSolo los perezosos no escribieron sobre el famoso juego de Eduard Luc en Habré. Parece que todas las cubiertas están arrancadas y ya no es posible agregar algo más sobre el algoritmo. Pero no, este tema tiene recursos ocultos. Hoy, en particular, vamos a rehacer el algoritmo para resolver este rompecabezas en una forma completa. (¿Por qué? Solo por diversión. Viernes posible).
Esta publicación está dedicada a la memoria del verdadero gurú de la programación Andrei Mrrl Astrelin, quien una vez me explicó este algoritmo de manera simple e inteligible. El pseudocódigo siguiente es el texto de su autoría.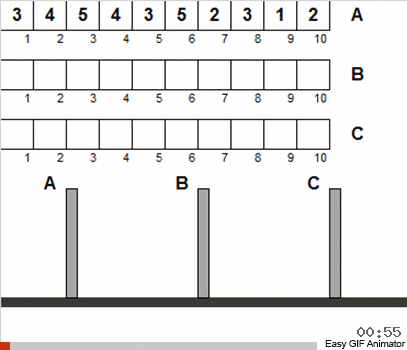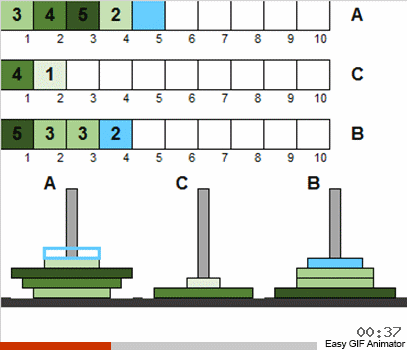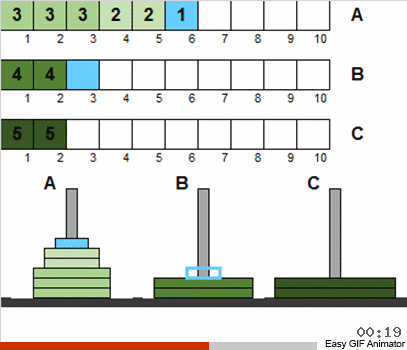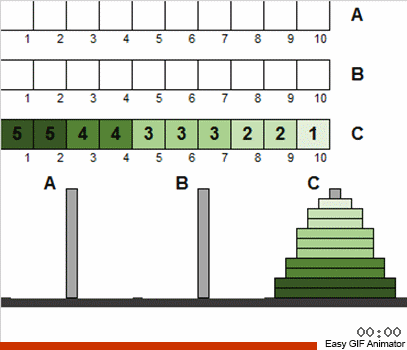
En el rompecabezas clásico, los discos en el primer poste se ordenan inicialmente. Pero permitiremos que se ensarten en cualquier orden.
Además, se supone que los tamaños de disco son únicos. No nos aferraremos a esta restricción y permitiremos repeticiones.
Si se permite solo estas dos libertades, las condiciones iniciales del rompecabezas se pueden interpretar como una matriz (los discos son números), y la tarea es que esta matriz necesite ser ordenada.
Las condiciones restantes que (casi) no cambian:
- Tenemos dos polos auxiliares (un par de matrices vacías).
- Podemos transferir discos uno a la vez.
- Poner solo los más pequeños a los más grandes (ya que hemos permitido los mismos tamaños de disco, también puede colocar el disco movido encima de otros del mismo tamaño).
- Tenemos derecho a comparar un disco portátil con solo los discos superiores (es decir, las 3 matrices son pilas).
Nuestra tarea: tomar el clásico algoritmo de rompecabezas recursivo ...
def hanoi(n, source, helper, target): if n > 0: hanoi(n - 1, source, target, helper) if source: target.append(source.pop()) hanoi(n - 1, helper, source, target)
... y convertirlo en una clasificación!
De hecho, desde el hecho de que permitimos el desorden inicial y las repeticiones para el tamaño de los discos, nada cambió fundamentalmente de esto. En general, el problema se resuelve de la misma manera recursiva clásica. Lo más importante a entender es que todos los movimientos del disco se dividen en varias etapas, cada una de las cuales es un clásico de Hanoi en miniatura.
Es decir, en cada etapa no consideramos todos los discos disponibles, sino solo la totalidad de aquellos que satisfacen las condiciones anteriores. Después de ordenar este pequeño conjunto por clásicos, acercaremos el estado general del sistema al rompecabezas clásico. Luego, nuevamente tomamos el conjunto de discos que corresponde a los clásicos y aplicamos nuevamente el algoritmo conocido. ¡Y este conjunto será mayor que en el paso anterior! Y así repetimos hasta que todos los discos en todos los polos de repente se vuelvan diferentes del estado clásico.
El sistema que se violó inicialmente (por el hecho de que los discos no están ordenados en la entrada) se repara automáticamente con cada iteración.
En cuanto a la resolución de repeticiones, esto no importa en absoluto. Debido a que los discos idénticos consecutivos simplemente nos movemos como un disco.
Algoritmo
Llamamos a las columnas
A ,
B ,
C (
A al principio no está vacío).
Presentamos las operaciones:
A ->
C (): cambia un disco de
A a
C.top (A) ,
top (C) : el tamaño del disco superior
A o
C. Si la columna está vacía, entonces este tamaño =
MaxInt .
B ->
C (
K ): cambie de
B a
C todos los discos cuyo tamaño sea menor que
K (podemos hacer esto si los discos superiores
A y
C no
son menores que
K ).
swap (): reorganice las columnas
B y
C (o cámbieles el nombre, no nos importa dónde estén los discos).
while (
A ) - repite hasta que
A esté vacío.
Entonces funciona el siguiente algoritmo:
©
MrrlDificultad
En el peor de los casos, la clasificación tiende a la complejidad del tiempo para el algoritmo clásico, que, aunque simple y elegante, es al mismo tiempo máximamente ineficiente. En cuanto al mejor y el promedio, me resulta difícil asumirlo.
En cuanto a la memoria, podemos decir que si se utiliza la recursividad, los costos serán los correspondientes.
Implementación
No he escrito mi propia versión en Python (lo haré más adelante). Sin embargo, en la sección "Enlaces" a continuación, publiqué algunos enlaces donde puede ver implementaciones en diferentes idiomas. Opción especialmente interesante en Java. El autor no tomó como base el conocido método recursivo para resolver el rompecabezas, sino que construyó el árbol de caminos más corto. Presumiblemente, esta es la solución más efectiva si escribe la clasificación al estilo de "Torre de Hanoi".
Características del algoritmo
Referencias
 Torre de hanoi
Torre de hanoiImplementaciones:
C ,
Java vs C ++ vs Python ,
Python .
Artículos de la serie:
En la aplicación AlgoLab, esta clasificación ya está disponible. Aunque pertenece a la clase de clasificaciones por inserciones, debido a la extravagancia del algoritmo, se ubica en la sección "Otras clasificaciones". También hay una limitación: los números en la matriz ordenada pueden ser solo del 1 al 5 (debido a la difícil representación de los discos). Otros números aún serán reemplazados por estos.
También hay un límite en el tamaño de la matriz: no más de 20 elementos. Esto se hizo exclusivamente en su propio interés: si toma una matriz que es demasiado grande, puede suceder que deba clasificarla a una edad muy avanzada.

Este artículo fue escrito con el apoyo de EDISON Software, una compañía que desarrolla profesionalmente la iluminación de ciudades inteligentes y mantiene sitios de Python.