Teoría de la felicidad. ¿Los accidentes no son accidentales?

Sigo familiarizando a los lectores de Habr con los capítulos de su libro "Teoría de la felicidad" con el subtítulo "Fundamentos matemáticos de las leyes de la maldad". Este libro de ciencia popular aún no se ha publicado, informa de manera muy informal acerca de cómo las matemáticas le permiten mirar el mundo y la vida de las personas con un nuevo grado de conciencia. Es para aquellos que están interesados ​​en la ciencia y para aquellos que están interesados ​​en la vida. Y dado que nuestra vida es compleja y, en general, impredecible, el énfasis en el libro se centra principalmente en la teoría de la probabilidad y las estadísticas matemáticas. Aquí no se prueban los teoremas y no se dan los fundamentos de la ciencia, de ninguna manera es un libro de texto, sino lo que se llama ciencia recreativa. Pero es precisamente un enfoque tan lúdico que nos permite desarrollar la intuición, alegrar las conferencias para los estudiantes con ejemplos vívidos y, por último, explicar a los no matemáticos y a nuestros hijos lo interesante que encontramos en nuestra ciencia seca.



En este capítulo, discutimos el vuelo predeterminado de monedas, mapas topográficos, desastres matemáticos y la naturaleza de la aleatoriedad. Y en el camino, veamos secciones de matemáticas como la teoría de las medidas y la teoría del caos dinámico.

La conversación sobre las leyes de la maldad, como fuente de confusión cotidiana, a menudo comienza con la famosa ley de un sándwich . Es simplemente formulado, fácilmente verificado y ampliamente conocido:

Un sándwich siempre deja caer mantequilla.

Está claro que la palabra "siempre" aquí es una exageración. Es fácil imaginar las condiciones en que caerá un sándwich, dejando intacto el lado aceitado. ¿Qué entiende la gente por esta ley? Lo más probable es que el sándwich se caiga la mantequilla con la frecuencia suficiente para que se note. Pero, ¿es más probable un resultado desfavorable de una caída que uno favorable? Los sándwiches son diferentes, caen en diferentes circunstancias, desde diferentes alturas ... Hay tantos parámetros que probablemente no tenga sentido hablar de patrones en una tarea de este tipo. Cualquier cosa puede pasar. Sucede que cae en el petróleo, luego se vuelve insultante, recordamos la ley y la recordamos. Y si el sándwich cae sin interés, con el aceite arriba, o si resulta que no tiene aceite, no hay nada de qué hablar, ¡está claro que la ley es cómica! Al final, un sándwich es como una moneda, que los matemáticos usan para obtener variables aleatorias con dos valores posibles: "águila" y "colas". Si la moneda es "honesta", entonces no importa de qué lado caer, y decimos que la probabilidad de que el águila y la cola caigan es igual e igual. $$$1/2$ . En teoría, los emparedados deberían ser lo mismo. Volveremos a ellos en el próximo capítulo, pero por ahora echemos un vistazo al sistema probabilístico simple más probable: la moneda.

Se lanza una moneda en experimentos teóricos de probabilidad de una manera mágica especial, de modo que la elección de la posición inicial, la velocidad inicial y la velocidad de giro durante el lanzamiento no afecta la probabilidad de un resultado específico. ¡Pero es obvio que esto es imposible! La moneda es un sistema mecánico y obedece las leyes de la mecánica, pero no contienen variables aleatorias. El futuro en las leyes del movimiento de un cuerpo tan simple como una moneda está determinado únicamente por el estado pasado de este cuerpo. Si un robot lanza una moneda, o el demonio de Laplace es una criatura mítica que tiene información completa sobre las coordenadas y las velocidades de cualquier sistema mecánico, se obtendrán resultados idénticos con datos iniciales constantes. Nosotros, por supuesto, no somos robots ni demonios, pero ¿la gente realmente arroja monedas tan descuidadas e impredecibles que las leyes de la mecánica pueden provocar accidentes?

¿Y de dónde, en general, proviene la aleatoriedad en el mundo descrito por las leyes de la mecánica? ¿De dónde viene el azar? ¿Cuál es la diferencia entre sistemas verdaderamente caóticos o estocásticos, fundamentalmente impredecibles, y sistemas en los que simplemente es difícil adivinar el comportamiento, pero se puede calcular?

El problema de la moneda fue considerado en 1986 por Joseph Keller. Proporcionamos una explicación simple para la ocurrencia de incertidumbre en este proceso, basada en el razonamiento del artículo de Keller. De qué lado caerá la moneda depende de su tiempo de vuelo. $$$t$ y de velocidad angular $$$\ omega$ . Si mide la velocidad angular en revoluciones por unidad de tiempo, entonces el número de revoluciones hechas por la moneda se expresa de manera extremadamente simple $$$n = t \ omega$ . Esta dependencia establece las líneas de un número igual de revoluciones en las coordenadas. $$$(t, \ omega)$ , y ellos, a su vez, limitan las áreas correspondientes a un número par e impar de revoluciones.

Un diagrama que muestra la paridad del número de revoluciones realizadas por una moneda en vuelo. El rectángulo muestra el área en la que ocurre con mayor frecuencia el proceso de adivinación en la moneda.

En dicho diagrama, es posible mostrar cuál será el resultado de un lanzamiento de moneda, retorcido por un número conocido de revoluciones por segundo, y capturado después de un tiempo de lanzamiento conocido. Si caemos en una franja blanca, se caerá el mismo lado que estaba encima al tirar, si está en naranja, lo contrario. Las líneas de igual velocidad son hipérbolas y se puede ver que a medida que aumenta la velocidad, la alternancia de áreas se vuelve más y más frecuente, y las áreas mismas se vuelven más delgadas. La mano humana es imperfecta y una dispersión muy pequeña de valores iniciales cubre muchas áreas a la vez, lo que hace que el resultado sea impredecible. En el rango de la mano (el rectángulo en el diagrama), un desplazamiento de suficiente $$$5 \%$ saltar de una franja blanca a una naranja. La pregunta sigue siendo: ¿cómo se sigue la "honestidad" de una moneda mecánica real de esta construcción? ¿Cómo obtener la probabilidad de pérdida de un águila o colas del diagrama resultante?

¡Toma medidas urgentes!

Nos sumergiremos un poco en las matemáticas que no se enseñan en la escuela para comprender mejor lo que estamos discutiendo. Dijimos en la introducción que los matemáticos no estudian números o formas geométricas, como podría parecer después de estudiar un curso escolar. Trabajan con estructuras matemáticas (álgebras abstractas, medios anillos, campos, monoides, espacios topológicos y otras cosas abstractas), las describen, como parece, completamente desapegadas para practicarlas, definirlas, estudiar sus propiedades, probar teoremas. Y luego perfeccionaron sus habilidades para encontrar tales estructuras en diversos campos del conocimiento, logrando avances sorprendentemente útiles, incluso en campos puramente aplicados. Ahora tocaremos un poco sobre tales matemáticas y consideraremos cómo se construye la base de la teoría de probabilidad basada en un concepto muy abstracto de medida.

Describimos la mecánica de la moneda y obtuvimos áreas que describen conjuntos de soluciones con ciertas propiedades. Las áreas son figuras planas, ¿cómo pasar de ellas a las probabilidades correctamente? Necesitamos medir nuestras áreas y naturalmente llegamos a su área. Área: es una medida de una figura plana. Este es un término matemático exacto para una función que asocia un conjunto con un cierto valor numérico no negativo. Ejemplos de medidas son las cantidades en conjuntos enumerados (el número de manzanas en una bolsa, por ejemplo), así como la longitud , el área y el volumen de las figuras .

Hay una sección completa en matemáticas llamada teorías de medida . Esta teoría nació a comienzos de los siglos XIX y XX (Emil Borel y Henri Lebesgue se encontraban en sus orígenes) y abrió oportunidades para que los matemáticos analizaran objetos muy complejos: conjuntos cantor y fractales. Formó la base del análisis funcional y la teoría de probabilidad moderna, cuyo fundamento fue establecido por el notable matemático ruso Andrei Kolmogorov. La definición de probabilidad, como medida, le permite ver todas las propiedades básicas de probabilidad para conjuntos discretos y continuos.

Aunque nuestro libro no es un libro de texto, vale la pena detenerse un poco para ver los conceptos de torio de probabilidad a vista de pájaro y sentir el sabor de las matemáticas. Para empezar, enumeramos las principales propiedades de cualquier medida. Para imaginarlos mejor, puede usar las palabras "cantidad" o "longitud" o "área" en lugar de la palabra "medida".

1. La medida del conjunto vacío es cero.
2. La medida de todo el conjunto medible es finita para medidas finitas.
3. La medida del subconjunto no excede la medida del conjunto
4. La medida de unión de dos conjuntos arbitrarios es igual a la suma de las medidas de estos conjuntos menos la medida de su intersección (aditividad).
5. La medida de complementar un subconjunto es igual a la diferencia de medidas de todo el conjunto y la medida del subconjunto.

¿Puede alguna función numérica no negativa ser una medida? En absoluto Por ejemplo, la edad le da a una persona un número completamente específico. Pero la edad de dos personas no puede definirse como la suma de sus edades. Y la velocidad de carrera no es una medida: dos personas corren no el doble de rápido. Pero el impulso (impulso) o energía ya tiene las propiedades de una medida. El peso, la cantidad de dinero, la cantidad de conocimiento, el volumen del llanto, aunque no siempre son cosas fácilmente medibles, también pueden servir como medida para muchas personas.

En un nivel intuitivo, casi todos están familiarizados con el concepto de probabilidad ahora. Los científicos políticos y periodistas lo estiman en programas de entrevistas, se discute hablando sobre el calentamiento global o la lluvia de mañana, se cuentan chistes al respecto: ¿Cuál es la probabilidad de encontrarse con un dinosaurio en el Tver? - Un segundo: ya sea una reunión o no. En las matemáticas modernas, el concepto de probabilidad se define como una medida en un conjunto especial llamado espacio de probabilidad . Incluye tanto eventos elementales como sus combinaciones obtenidas utilizando las operaciones de unión, intersección y exclusión. Un ejemplo de un evento elemental: "pérdida de un triple al tirar un hueso". Un ejemplo de un evento que no es elemental: "la pérdida de cualquier número par excepto dos". Entonces, enumeramos las propiedades de probabilidad:

1. La probabilidad de un evento imposible es cero.
2. La probabilidad para todo el espacio de probabilidad es igual a la unidad.
3. Si un evento también implica otro, entonces la probabilidad del segundo no excede la probabilidad del primero. Aquí la relación "implica" para eventos es equivalente a "es un subconjunto" para conjuntos y no significa "es una causa".
4. La probabilidad de ocurrencia de al menos uno de dos eventos arbitrarios es igual a la suma de las probabilidades de cada uno de estos eventos, menos la probabilidad de que los eventos ocurran simultáneamente.
5. La probabilidad de que un evento no ocurra es uno menos la probabilidad de que ocurra un evento.

Observe más de cerca las propiedades de las medidas y las probabilidades y verá que estamos hablando de las mismas propiedades.

No todas las propiedades de probabilidad surgen de su definición como medida: los conceptos de independencia de eventos y el método para calcular la probabilidad de dos o más eventos independientes simultáneamente a medida que los productos de probabilidades se introducen a través de la probabilidad condicional , pero estos conceptos son consistentes con la definición de Kolmogorov.

Las variables aleatorias discretas corresponden a conjuntos contables finitos; en ellas, una medida natural es un recuento ordinario del número de elementos. En consecuencia, la probabilidad en un espacio probabilístico discreto es el cálculo combinatorio de opciones que es familiar para todos los estudiantes. Para variables aleatorias continuas, la probabilidad, como medida, es más como longitud o área, y aquí estamos hablando de densidades de probabilidad .

La analogía de probabilidad con medida no termina ahí. ¿Cuál es el valor promedio ? Este es un análogo de la posición del centro de masa de una figura que consiste en masas puntuales o un sólido con una densidad conocida. Y estas cantidades se calculan de la misma manera. ¿Y cómo se caracteriza la dispersión de variables aleatorias alrededor del promedio: varianza ? Al igual que el momento de inercia caracteriza la distribución de masa alrededor del centro de masa. Y nuevamente, las fórmulas para calcular la varianza de una muestra o distribución coinciden con las fórmulas para el momento de inercia de un conjunto de cuerpos o un cuerpo sólido de una forma astuta.

Por cierto, si reemplazamos en las definiciones y propiedades de probabilidad la suma con "máximo" y el producto con "mínimo", entonces podemos construir una teoría alternativa, llamada teoría de posibilidades . Así es como funcionan las matemáticas. Comenzamos con un razonamiento abstracto: los números forman un álgebra con operaciones de suma y multiplicación, pero en un intervalo de número limitado, puede construir un álgebra similar con operaciones de mínimo y máximo. ¡Construimos el concepto de medida sobre un nuevo álgebra y descubrimos que abre una nueva visión del mundo! A diferencia de la teoría de la probabilidad, en dicha teoría se pueden construir dos medidas coordinadas: la posibilidad y la necesidad y, a diferencia de la probabilidad, están en buen acuerdo con las operaciones de combinar e intersectar eventos. Esta dirección fue creada por el estadounidense Lotfi Zadeh, de origen azerbaiyano, que sirve de base para la lógica difusa y se utiliza en el reconocimiento automático de patrones y en los sistemas de toma de decisiones.

Increíble, pero cierto!

La primera propiedad de las medidas parece trivial, pero es interesante en su asimetría. Si la medida del subconjunto es cero, ¡esto no significa que esté vacío! Por ejemplo, una línea es un subconjunto de los puntos en un plano, pero su área (medida) es cero. Hay ejemplos más exóticos: conjuntos de Cantor y fractales que tienen una estructura compleja, contienen un número infinito de puntos, visiblemente "ocupando" un área o volumen determinado, pero sin embargo tienen una medida cero.

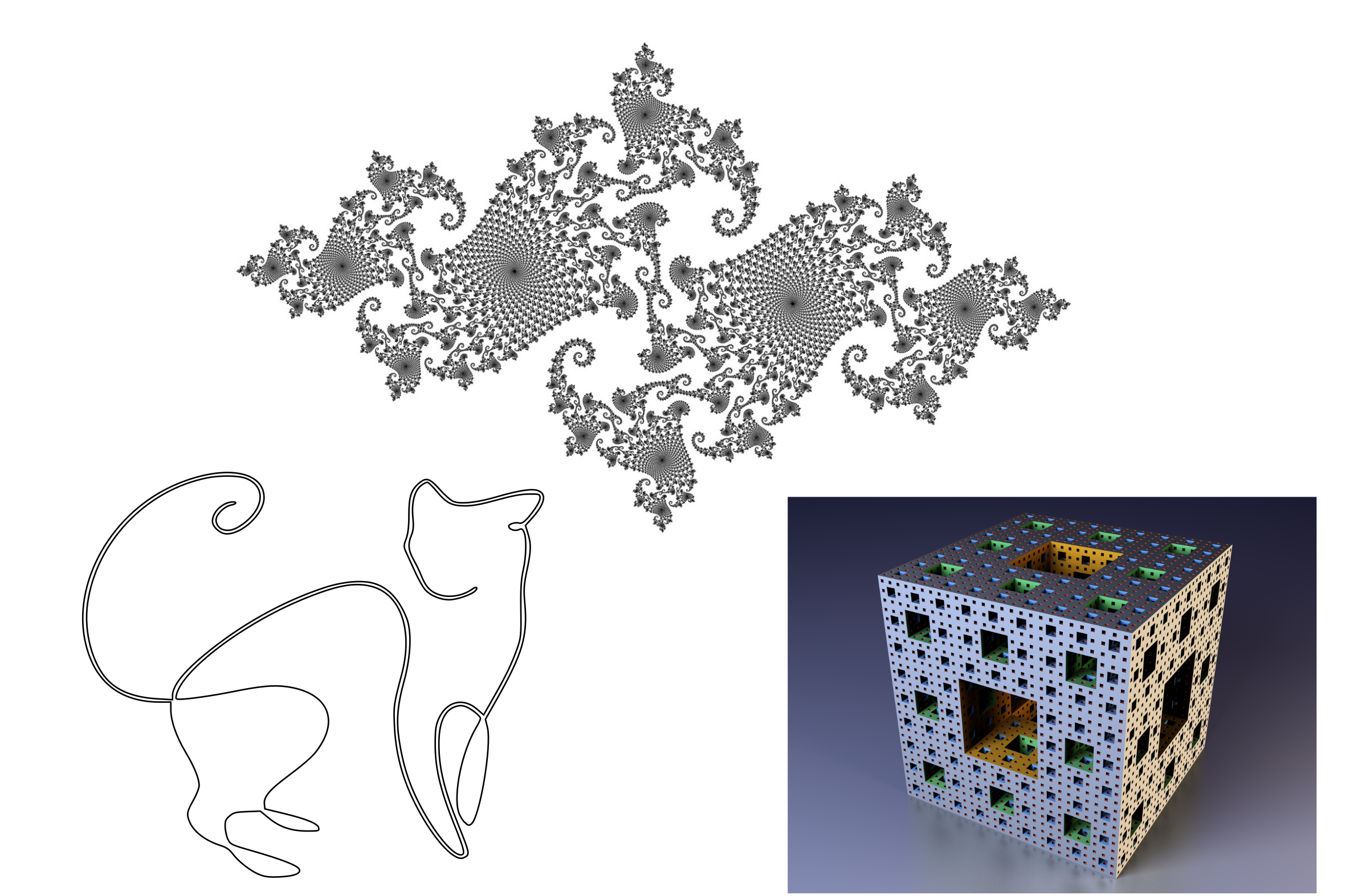Algunos objetos de medida cero: una línea en un plano, un conjunto esporádico de Julia, una esponja fractal Menger.

Mientras preparaba esta ilustración, encontré una imagen maravillosa de un conjunto desconectado de Julia en un fondo transparente con alta resolución. Después de insertarlo en el editor de vectores, me encontré con una dificultad divertida: era muy difícil ingresar a esta imagen con el mouse para seleccionarla. Es tan "suelto" que la probabilidad de entrar en un píxel lleno fue notablemente menor que entrar en un fondo transparente. En el espacio de probabilidad, también pueden existir subconjuntos de medida cero, pero esto no significa que los eventos de estos subconjuntos sean imposibles. Del cuarto al quinto intento, aún podría seleccionar la imagen, ya que los píxeles tienen un tamaño finito. Pero, ¿qué pasaría si tuviera a mi disposición un conjunto incoherente real de Julia con resolución infinita?

Imagine que está utilizando un generador de números aleatorios de software que produce un número real arbitrario de $$$0$ antes $$$1$ . ¿Cuál es la probabilidad de que un número se caiga? $$$0$ ? y números $$$1/2$ o $$$e / \ pi$ ? En todos estos casos, la respuesta será: ¡cero! Más bien, el número positivo más pequeño disponible para la computadora, la llamada máquina épsilon, porque la computadora funciona con un número finito de decimales. Espera, dices, ¿en qué sentido es cero? Los mismos números no son imposibles. Realicemos un experimento, como resultado obtenemos un número específico, y cuando lo obtenemos, "por construcción" la probabilidad de su aparición no puede ser cero. Así es, pero ¿cuánto tiempo debo esperar hasta que salga exactamente 0? Casi sin fin! El hecho es que un solo número, como un punto en un segmento, tiene una medida cero y una probabilidad cero honesta. Solo una medida de un segmento continuo, incluso uno muy pequeño, no es cero. Entonces, no estamos hablando de probabilidad, sino de densidad de probabilidad, que, cuando se multiplica por una medida finita de un subconjunto en un espacio de probabilidad, dará un valor finito: la probabilidad de caer en este subconjunto. Por cierto, resulta ser nuestro generador ideal de números aleatorios con una precisión infinita, la probabilidad de obtener algún número racional (no algo concreto, pero ninguno) también será cero. La prueba de que los números racionales forman un subconjunto denso de la medida cero del conjunto de números reales hizo ruido a fines del siglo XIX.

Si alguien realiza pacientemente miles de experimentos con una moneda y felizmente le dice que obtuvo tantas "águilas" como "colas", puede expresar con seguridad sus dudas o felicitarlo por su rara suerte. Si bien arrojar una moneda y un proceso aleatorio discreto, a medida que se acumulan las estadísticas, el poder del espacio de probabilidad aumentará y la medida del evento: "el número de" águilas "coincide con el número de" colas "" disminuirá. Se puede demostrar, usando la fórmula de Stirling, que la probabilidad de este evento "más probable" tiende a cero con un aumento en el número de pruebas como $$$1 / \ sqrt {\ pi n}$ . Para cien lanzamientos, esto es un poco más del cinco por ciento, para diez mil, solo medio por ciento. En tales casos, los matemáticos dicen: casi con certeza el número de "águilas" no será igual al número de "colas" . No importa cuán extraño suene, pero "casi con certeza" es un término matemático exacto, lo que significa que el evento es un complemento de un subconjunto del espacio de probabilidad de medida cero. Volveremos a estas consideraciones en uno de los siguientes capítulos cuando nos preguntemos: cuánto podemos considerar normales cada uno de nosotros.

Comprobando la honestidad de una moneda real

. ( ) ( «» «» ). , , .

! ( ). , , . $$$\omega = n/t$ . $$ω = 1 / t es igual$\omega = 1/t$$$S , entonces debido a la propiedad de aditividad, el área bajo la curva$S$$$ω = n / t será igual$\omega = n/t$$$$S_n = n S$ . A su vez, para tiras individuales obtenemos: $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ .Resulta que la diferencia en el área no depende del "número" de la hipérbola. Esto no es algo especial con respecto a las hipérbolas; se puede sacar la misma conclusión para cualquier curva de la forma$$y = n f ( x ) , si solo la función$y = n f(x)$$$f fue medible. Y si es así, para toda el área de definición, entrar en la parte blanca del diagrama o en el sombreado es igualmente probable, como se esperaba para una moneda "honesta". Los argumentos que acabamos de citar parecen bastante simples, pero dan un resultado muy general, aplicable a cualquier cantidad de aditivos. El concepto abstracto de medida nos permitió comparar cantidades infinitas entre ellos, mientras permanecíamos dentro del marco de la lógica y el sentido común. La abstracción es buena, pero se puede argumentar que en realidad no estamos lanzando monedas con todos los parámetros posibles. Como mostraron los experimentos con una cámara de alta velocidad, las velocidades angulares caen en el rango de$f$



$$20 a$20$$$40 revoluciones por segundo, y la duración del vuelo es de medio a un segundo. Esta área está resaltada por un rectángulo en el diagrama. En ella, el área total de las franjas blancas es ligeramente mayor que las de color naranja, y podemos concluir que la probabilidad de caerse del mismo lado que estaba durante el lanzamiento será$40$$$$50.6\%$ .

2007 , . , , , — , , « », «» .

? , ? , , , , : $$σμ=σ/√n aquí$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ es la desviación estándar para la distribución estudiada. En nuestro caso, para la distribución de Bernoulli con probabilidad$\sigma$$$0.51 que es igual$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ . Para identificar con confianza la desviación del promedio de una centésima, esta desviación debe exceder $$3 desviaciones estándar. Por lo tanto, podemos estimar el número de ensayos:$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

, . , , «», , , . $$$40000$ «». «» «» , , , , .

.

, $$20,000 pruebas de la "nube" de valores medios observados comienzan a separarse claramente. Bueno, para uso doméstico, podemos suponer que la moneda es un buen generador de una elección aleatoria de dos opciones igualmente probables.$20000$

Derecho de turismo

La equivalencia de la determinación de probabilidad geométrica y de frecuencia revela el misterio de una ley de la maldad, conocida entre los turistas, geólogos y todos aquellos que usan mapas topográficos:

El lugar donde va el turista suele estar en el pliegue del mapa o en el borde de la hoja.

Supongamos que estamos igualmente interesados ​​en objetos ubicados en todas las partes del mapa. Pero rara vez nos interesan los objetos de medida cero: el objetivo de usar un mapa es examinar los alrededores del objeto, es decir, un área finita. Deja que una pequeña fracción sea suficiente para nosotros$$α del área de todo el mapa$\alpha$$$S para descubrir cómo llegar al objeto. Entonces, si el objeto se acerca a una curva o borde a cierta distancia crítica$S$$$d , consideraremos la ley turística cumplida. La participación de las áreas fronterizas en el área total del mapa nos dará la oportunidad de experimentar esta ley de maldad en nosotros mismos. Así se ven las partes desagradables del mapa cuando$d$$$α = 0.5 % y en una curva.$\alpha=0.5\%$

El gris indica áreas "malas". Una gráfica con un área de medio por ciento para una tarjeta de 40 cm de ancho se muestra por separado, tiene un diámetro ligeramente superior a 3 cm.

Para una tarjeta cuadrada$$$d = \sqrt{\alpha S}$ . Las tiras desagradables tendrán un área $$$d \sqrt{S} = S\sqrt{\alpha}$ .Cuatro franjas, dos verticales y dos horizontales, se ubicarán en el borde, cualquier curva adicional, horizontal o vertical, agregará otra franja. Al mismo tiempo, las tiras de intersección agregan cuadrados adicionales con un área$$$d^2 = \alpha S$ . Doblando la tarjeta para que resulte $$$n$ horizontal y $$$m$ curvas verticales, obtenemos el área total de la zona desagradable igual a: $$$S (n + 2) \ sqrt {\ alpha} + S (m + 2) \ sqrt {\ alpha} -S (n + 2) (m + 2) \ alpha$ . Llevándolo al área de todo el mapa, obtenemos una parte desagradable del área total:

$$

$$p = (n + m + 4) \ sqrt {\ alpha} - (n + 2) (m + 2) \ alpha.$$

La figura muestra las áreas en las que esta proporción excede $$$50 \%$ para varios valores $$$\ alpha$ .

Áreas en las que hay una mayor probabilidad de estar en el pliegue de un mapa o en su borde Los números indican la fracción del área del vecindario considerado del área de todo el mapa.

Resulta que una tarjeta doblada por la mitad dos veces ya puede considerarse formalmente deshonesta en relación con un turista. Muy a menudo, las tarjetas tienen tres pliegues verticales y tres horizontales, lo que da la probabilidad de cumplir la ley de maldad con una probabilidad de aproximadamente $$$60 \%$ a las $$$\ alpha = 0.5 \%$

¿De dónde viene el azar?

En las tiendas de souvenirs puedes encontrar péndulos magnéticos para "elegir los deseos". Ellos también son generadores aleatorios mecánicos y a veces se los llama erróneamente "péndulos caóticos". Después de comenzar el movimiento desde una posición y velocidad iniciales, el péndulo realiza una serie de oscilaciones "impredecibles" y finalmente se detiene en uno de los sectores. Sin embargo, las fluctuaciones aquí no son impredecibles, simplemente son muy sensibles a las condiciones iniciales. Para cada sector en el que el péndulo puede detenerse, hay una región de atracción en el espacio de velocidad de coordenadas. Este es un conjunto de tales condiciones iniciales bajo las cuales el péndulo necesariamente se atraerá a un cierto punto en el sector indicado. El punto de parada del péndulo se llama atractor , un punto de atracción. En el caso de un péndulo de la imagen, el espacio de coordenadas y velocidades es de cuatro dimensiones, por lo que no es fácil mostrar el área de atracción. Pero si nos limitamos a solo dos sectores y reducimos el problema a unidimensional (tal péndulo se llama oscilador Duffing), entonces el espacio de valores iniciales se convertirá en un plano, de modo que se puedan ver las regiones de atracción. Parecen un símbolo intrincado de Yin-Yang, que se convierte rápidamente en tiras estrechas que separan las áreas de atracción.

Áreas de atracción de los atractores para un péndulo de deseos unidimensional: el oscilador Duffing.

Como en el caso de la moneda, cambiando ligeramente las condiciones iniciales, pasamos de un atractor a otro. Los dados y la ruleta funcionan de la misma manera, pero no son en sí generadores aleatorios. Estos no son sistemas verdaderamente caóticos y su comportamiento puede calcularse con precisión.

Pero, ¿qué es la posibilidad real? Un buen ejemplo de un verdadero sistema estocástico es la aparición de automóviles en la carretera. La gente no está de acuerdo, no coordina sus planes, cada elemento del conjunto fuera del camino actúa de forma independiente. Y aunque hay ciertos patrones en el comportamiento de las personas: horas punta en la mañana y en la noche, carreteras vacías en la noche, etc., no tenemos y nunca tendremos suficiente información sobre cada participante en el movimiento para predecir la aparición de ninguno de ellos. La mecánica de las partículas elementales a nivel cuántico, la descomposición de los átomos inestables, los cambios en el código genético, muy probablemente, los terremotos y las cotizaciones bursátiles en la bolsa de valores, también son estocásticos. Lo único que le queda al investigador es considerarlas como variables aleatorias y describirlas en términos de teoría de la probabilidad.

Pero hay otra fuente de oportunidad: el caos dinámico . Los sistemas caóticos difieren de los estocásticos en que se describen mediante ecuaciones y parámetros exactos que no contienen aleatoriedad. Sin embargo, su comportamiento no solo es complicado, sino caótico y verdaderamente impredecible. Si comenzamos a oscilar el péndulo de los deseos, con mucho cuidado, con frecuencia y amplitud controladas con precisión, descubriremos que sus movimientos suaves no pueden calcularse durante mucho tiempo. Ningún algoritmo en computadoras arbitrariamente precisas nos permitirá calcular el comportamiento exacto del péndulo para un futuro arbitrariamente distante. No se detendrá en ningún sector, pero hará movimientos suaves, pero nunca volverá al mismo punto en el espacio de velocidad de coordenadas dos veces. Otro ejemplo de un sistema caótico extremadamente simple es una pelota ideal que rebota en el campo de gravedad en una mesa ideal con un resorte. Las ecuaciones de Lorentz relativamente simples mostraron que nunca podemos predecir el clima durante más de un par de semanas; este también es un sistema caótico.

La teoría del caos dinámico fue capaz de explicar la naturaleza de tal imprevisibilidad. El simple péndulo unidimensional de los deseos, que examinamos, tenía dos puntos estacionarios estables: dos atractores y uno inestable, del cual el sistema está tratando de escapar, se muestra mediante un círculo blanco. En el modo caótico, en lugar de un conjunto de atractores, aparece un número infinito de trayectorias estacionarias inestables en el sistema. Este conjunto es infinito, pero tiene una medida cero y es una estructura disjunta muy complicada. Una vez en una de estas trayectorias, en principio es imposible seguirla utilizando algoritmos finitos. Pero lo más sorprendente, ¡resultó que este número infinito de trayectorias inestables en sí mismo es atractivo! 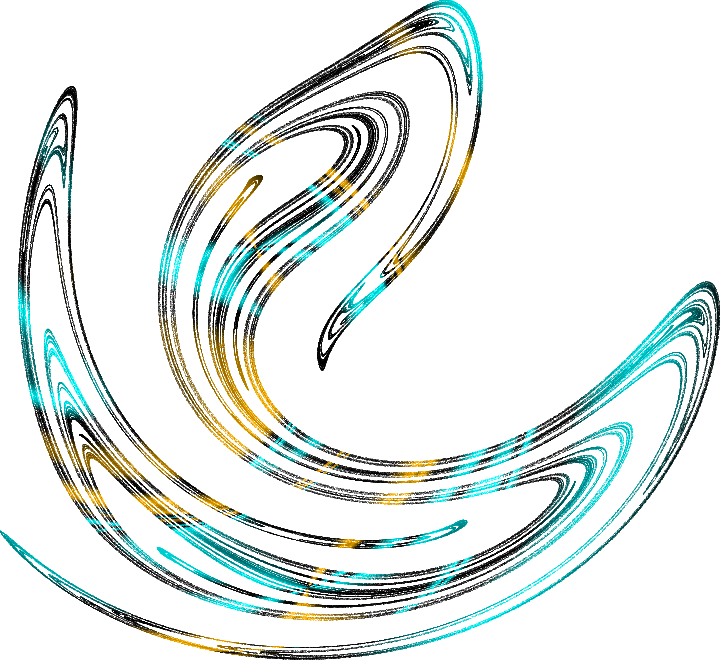El sistema caótico salta continuamente desde la vecindad de una trayectoria inestable a otra, todo el tiempo permaneciendo dentro de los límites de este extraño atractor. Entonces estos conjuntos se llaman atractores extraños . Así es como la sección de un atractor extraño para un péndulo de deseos, sujeto a oscilaciones armónicas, se ve fascinantemente hermosa. Este objeto para un péndulo unidimensional se puede describir en un espacio tridimensional (coordenadas, velocidad, fase de oscilación forzada). Si corta un atractor en este espacio por un plano, puede ver su estructura, esto se llama la sección de Poincare . Cada punto aquí es un rastro de la trayectoria, y el color de los puntos refleja la velocidad relativa con la que las trayectorias se dispersan entre sí. Aquí hay un par de atractores extraños hermosos:


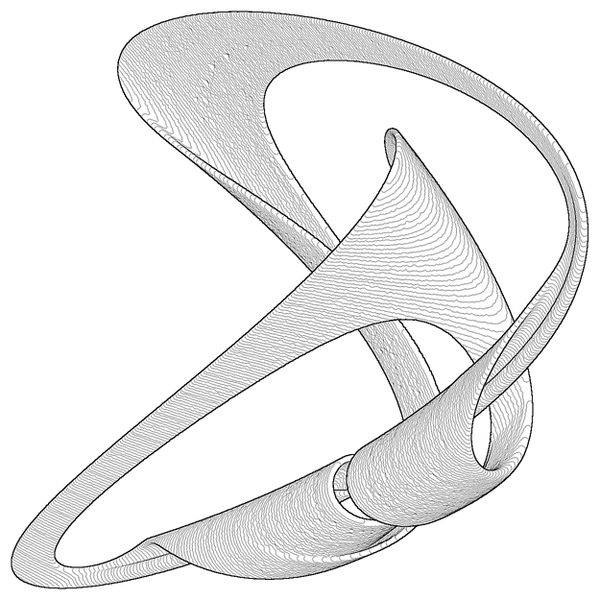Izquierda: sección de Poincare para la trayectoria de una pelota que rebota en una mesa con resorte. Muchos puntos pertenecen a la superficie de la esfera correspondiente a la ley de conservación de la energía. Derecha: una región volumétrica que encierra un atractor extraño que nace durante las vibraciones forzadas de una placa gruesa.

La suavidad de la trayectoria caótica le permite mirar un poco hacia el futuro. Esto explica una observación molesta: por un lado, los pronosticadores del clima a veces no pueden predecir con confianza el clima durante una semana, pero por el otro, si dice que mañana será el mismo clima que hoy, entonces no se equivocará en aproximadamente tres de cada cuatro casos . En general, las bromas sobre los pronosticadores del clima son injustas y debemos rendir homenaje al pensamiento humano y la perseverancia, ¡lo que hizo posible predecir el clima a un nivel moderno!

El caos dinámico es muy complejo y hermoso como teoría, da lugar a imágenes de increíble elegancia, pero también puede ser útil. Por ejemplo, los algoritmos mediante los cuales se generan números aleatorios en las computadoras también son deterministas. Para los ejemplos en este libro, utilicé un generador de números pseudoaleatorios que no inició el proceso estocástico real (desintegración alfa o contar autos en la carretera), pero calculé el siguiente número "aleatorio" en base a los anteriores que recibió antes.

De monedas a mariposas y al destino mismo

Las observaciones de cómo las pequeñas desviaciones se convierten en cambios globales en el sistema conducen al pensamiento del "efecto mariposa". Permítame recordarle que este efecto significa una cadena de consecuencias dramáticas de largo alcance de algún evento insignificante, a primera vista. Aplastada por investigadores del pasado, la mariposa en el cuento corto de Ray Bradbury "Y el trueno golpeó" condujo a una reestructuración radical del futuro. Y una de sus conferencias, Edward Lorenz, creador de la teoría del caos dinámico, titulada: "¿Puede un aleteo del ala de una mariposa en Brasil causar un tornado en Texas?"

Nos referimos implícitamente a este efecto, lamentando: "¡Si no hubiera doblado la esquina, todo habría sido diferente!", "¡Si no hubiera abordado este tren, no habría habido catástrofe!" o "¡Debido a tales pequeñeces, se pelearon y se separaron!" Pero vemos que un mundo cuántico verdaderamente estocástico y relojes atómicos ultraprecisos coexisten en el mundo, sistemas hamiltonianos estables en el mundo de las estrellas y galaxias y el caos de los anillos de Saturno o los anillos de Kuiper, el movimiento térmico de las moléculas y la sorprendente precisión del funcionamiento de los sistemas biológicos o los mecanismos de los automóviles. No, la aleta del ala de una mariposa no da lugar a huracanes, pero desaparece sin dejar rastro, dando lugar a una cadena de vórtices que transmiten energía e información a vórtices cada vez más pequeños, hasta que tanto la energía como la información desaparecen en el caos de las fluctuaciones. Debe entenderse claramente que las pequeñas desviaciones conducen a una reestructuración fundamental del sistema solo si es inestable o si el sistema está al borde de una bifurcación o catástrofe : esto es lo que los cambios globales en el comportamiento del sistema se llaman en el lenguaje de las matemáticas con pequeños cambios en los parámetros. Y las bifurcaciones siempre forman conjuntos de medida cero en el espacio de parámetros: estos son puntos o límites. Las pequeñas perturbaciones no conducen a desastres en casi todas partes (este también es un término exacto que significa "en todas partes, excepto un conjunto de medida cero"), y los estados inestables en la naturaleza rara vez se observan sin pasar la "prueba del tiempo".

Si la pareja se separó "por tonterías", estaba destinada a romper en cualquier caso, era inestable. Las parejas estables atraviesan guerras y hambrunas, y luego, a veces, se separan, pero no por pequeñeces, sino como resultado de cambios profundos que pueden sucederle a una persona durante su vida. En la cadena de eventos que llevaron al choque del tren, no es fácil identificar un evento clave (un error específico o un accidente fatal) y, lo más probable, la clave no es un evento, sino una violación sistemática de las reglas, lo que lleva al sistema a un estado inestable. Si hay muchos parámetros en el sistema, y ​​algunos de ellos son aleatorios, y nuestra vida está estructurada de esa manera, entonces la información en ese sistema tiende a perderse, y no será posible restaurar en qué momento exacto de nuestra vida "todo salió mal". No te atormentes con remordimientos por lo que sucedió, pero mira más de cerca lo que te está sucediendo ahora, para no perderte el verdadero punto de la bifurcación.

En este sentido, podemos recordar una de las leyes de la merfología, llamada ley de restauración por un cierto Dreisen:

El tiempo de mejora de la situación es inversamente proporcional al tiempo de su deterioro.

La siguiente observación se da como ejemplo: lleva más tiempo pegar el jarrón que romperlo. Esta ley describe sorprendentemente con precisión la relación entre las tasas características para el proceso de relajación de un sistema estable, que puede describirse mediante una ley exponencial decreciente $$$e ^ {- \ lambda t}$ y la tasa de desarrollo del proceso catastrófico en un sistema inestable, en la aproximación lineal: el crecimiento exponencial de una pequeña perturbación $$$e ^ {\ lambda t}$ . Estas velocidades son de hecho inversamente proporcionales entre sí. Sin embargo, el ejemplo del florero no es la relajación, una transición al estado más probable. Está más cerca de otro proceso: la autoorganización , este proceso, como primera aproximación, está descrito por la ley de logística y está más cerca de la velocidad de relajación que del desastre.

Procesos no estacionarios típicos: desastre, relajación y autoorganización, que tienen el mismo tiempo característico.

$$

$$* * *$$

A veces, caminando en la nieve, me sorprende que me caiga un copo de nieve en la nariz. Me sorprende que la probabilidad de este evento fuera insignificante. A juzgar por ello, ella nació en lo alto del cielo sobre el Océano Pacífico, rodeada de erráticas corrientes turbulentas en la nube, cayó continuamente cambiando de dirección ... ¡hasta llegar a la punta de mi nariz! ¿Y qué camino impresionante recorrieron los fotones desde una estrella distante? ¡Durante decenas de miles de años corrieron por el Universo, no fueron tragados por el polvo, no se encontraron con un asteroide! Nacieron en el mundo cuántico de una estrella distante, y terminaron su viaje en el mundo cuántico de la proteína opsina en la retina de mi ojo. No tiene sentido siquiera considerar la probabilidad de este evento, es cero, pero el evento ocurre y veo la luz parpadeante de una estrella. Ahora está claro que todo esto se debe a que el área de mi nariz e incluso las moléculas tienen una medida distinta de cero, pero aún así es sorprendente: ¡lo que casi seguramente no debería haber sucedido sigue sucediendo!

Dejemos que los filósofos discutan sobre el destino predeterminado o accidental, la verdad o el fantasma de nuestro conocimiento de la naturaleza. Insto al lector a mirar el mundo desde la altura de las abstracciones matemáticas y admirar su belleza y consistencia.