Lógica de tres valores
Lista de logros
- Puertas lógicas ternarias básicas: T_NOT, T_OR, T_AND, T_NAND, T_NOR, T_XOR y más
- Síntesis, minimización y realización de funciones ternarias
- Media víbora ternaria, víbora completa ternaria, víbora transportadora de ondas ternarias
- Subtractor completo ternario, comparador, multiplicador, multiplexor / demultiplexor
- Chanclas y cierres ternarios
- Una primitiva unidad aritmética y lógica ternaria (ALU)
Convenciones y tecnologías utilizadas
- Se utilizó ternario desequilibrado (0, 1, 2) en la implementación
- 1 Trit se expresa en 2 Bits: 0 ~ 00, 1 ~ 01, 2 ~ 10 (11 no está definido)
- Modelo Sim, Quartus prime, Logisim
Introduccion
Como estudiantes de primer año de la Universidad de Innopolis, tuvimos la oportunidad de realizar proyectos a lo largo de nuestro curso de arquitectura informática. Nuestro grupo estaba particularmente interesado en el sistema ternario y su funcionamiento, por lo que decidimos implementar un sistema ternario simple con componentes básicos (compuertas).
En lógica, una lógica de tres valores (también lógica trinaria, trivalente, ternaria) es uno de varios sistemas lógicos de muchos valores en los que hay tres valores de verdad que indican verdadero, falso y algún tercer valor indeterminado.
La lógica ternaria es compatible con MVL (lógica multivalor ). Sin embargo, solo se utilizan tres estados lógicos, ' 0 ', ' 1 ' y ' 2 '. Se encuentra que la raíz óptima ( r ) de un número fraccionario es el logaritmo natural ( e ). La lógica ternaria usa representación numérica con r = 3 , en comparación con la lógica binaria que usa r = 2 , por lo tanto, la raíz entera más económica que es la más cercana al logaritmo natural e , es la base 3. Esta propiedad especial de la base 3 inspiró la computadora primitiva diseñadores para construir una computadora ternaria.
La primera computadora ternaria que funcionaba fue construida en Rusia en la Universidad Estatal de Moscú en 1958. La computadora fue diseñada por Nikolay Brusentsov y sus colegas. Lo llamaron Setun , como el río que fluye cerca del campus universitario.
Lógica ternaria
Una función lógica ternaria es un mapeo F: {0,1,2} n -> {0,1,2} . Discutiremos las ventajas y desventajas de la lógica ternaria sobre la lógica binaria.
Cuando la lógica booleana tiene 2 2 = 4 operadores unarios, la adición de un tercer valor en la lógica ternaria conduce a un total de 3 3 = 27 operadores distintos en un solo valor de entrada. Del mismo modo, donde la lógica booleana tiene 2 2 2 = 16 operadores binarios distintos (operadores con 2 entradas), la lógica ternaria tiene 3 3 2 = 19,683 de dichos operadores. Cuando podemos nombrar fácilmente una fracción significativa de los operadores booleanos (no, y, o, nand, ni, exclusivos o, equivalencia, implicación), no es razonable intentar nombrar todos menos una pequeña fracción de los posibles operadores ternarios.
Ventajas de la lógica ternaria
Una representación lógica ternaria permite una codificación de información más compacta y eficiente que la representación lógica binaria equivalente. El argumento enunciado es el siguiente: si suponemos que un circuito digital tiene N posibles combinaciones de entrada, entonces un circuito binario requiere log 2 N líneas de entrada y un circuito ternario requiere log 3 N líneas de entrada.
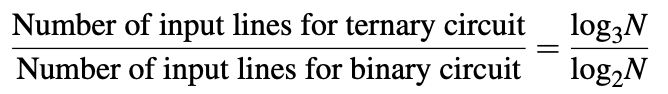

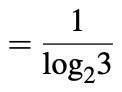

Por lo tanto, una implementación codificada ternaria de una función lógica binaria dada debería requerir 0.63 veces las líneas de entrada que la implementación binaria correspondiente.
Desventajas de la lógica ternaria
Aunque los circuitos lógicos ternarios deberían requerir menos líneas de entrada que los circuitos lógicos binarios equivalentes, los circuitos lógicos ternarios actualmente no son una opción práctica. Las razones son
- La tecnología de implementación de hardware ternario aún se encuentra en los niveles teóricos, de simulación y de pruebas de laboratorio.
- Representar tres niveles lógicos ternarios (0, 1 y 2) utilizando niveles de voltaje de tecnología existente aún no está definido de manera efectiva
- No se desarrolla ningún modelo computacional ni lenguaje de programación. Sin embargo, la simulación de resultados de la implementación de circuitos ternarios utilizando semiconductores de óxido metálico complementario (CMOS), diodos de túnel resonantes (RTD) y tecnologías de nanotubos de carbono, demuestra que la lógica ternaria puede ser una opción para la computación futura.
Diversas representaciones posibles para el sistema ternario.
- Sistema de numeración ternario (ternario desequilibrado) , cada dígito es un trit (dígito trinario) que tiene un valor de: 0, 1 o 2
- Ternario equilibrado , cada dígito tiene uno de 3 valores: −1, 0 o +1; estos valores también pueden simplificarse a -, 0, +, respectivamente (más comúnmente utilizado)
- Representación binaria redundante , cada dígito puede tener un valor de −1, 0, 0/1 (el valor 0/1 tiene dos representaciones diferentes)
- Incline el sistema de números binarios , solo el dígito distinto de cero más significativo tiene un valor 2, y los dígitos restantes tienen un valor de 0 o 1
Más sobre el sistema de numeración ternario equilibrado
Hoy en día, casi todo el hardware está diseñado para computación binaria. Si tuviéramos un componente electrónico estable con tres estados estables, el mundo quizás habría recurrido a la informática ternaria. Sin embargo, esta no es la verdad hoy. La notación equilibrada de la raíz ternaria tiene algunas propiedades beneficiosas:
- La inversión ternaria es fácil, solo intercambie −1 con 1 y viceversa. Si usamos un ejemplo, 24 se representa como 1T0 y -24 como T10 en notación ternaria equilibrada (T es simplemente una notación para -1). Esto es más simple que la regla para el complemento de dos en lógica binaria.
- El signo de un número viene dado por su 'trit' distinto de cero más significativo
- La operación de redondeo al entero más cercano es idéntica al truncamiento.
- La suma y la resta son esencialmente la misma operación (es decir, simplemente agrega los dígitos usando las reglas para la adición de dígitos)
Ejemplos:
21 10 = 1T10 3 ; 296 10 = 11T00T 3 ;
-24 10 = T10 3 ; -137 10 = T110T1 3
Aritmética ternaria
La aritmética ternaria puede ofrecer una notación más compacta que la aritmética binaria, y habría sido una opción obvia si los fabricantes de hardware hubieran encontrado un interruptor ternario.
Suma ternaria equilibrada y multiplicación
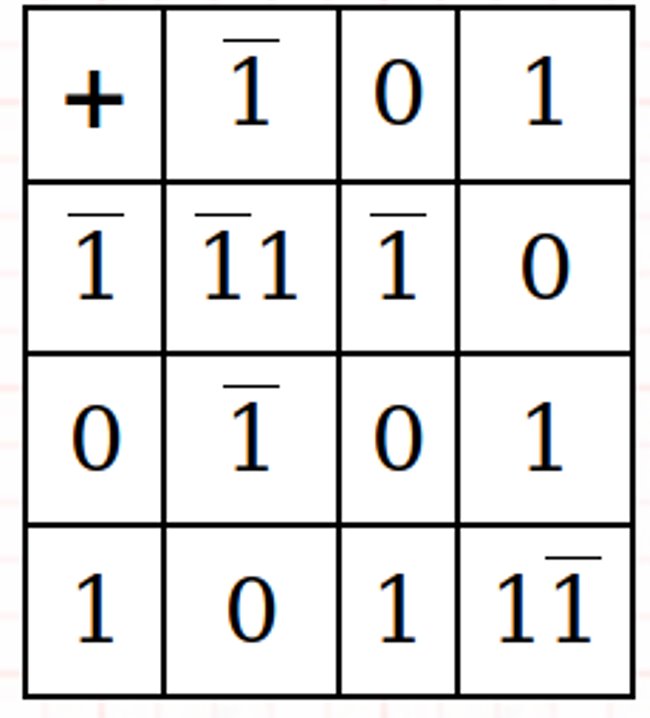
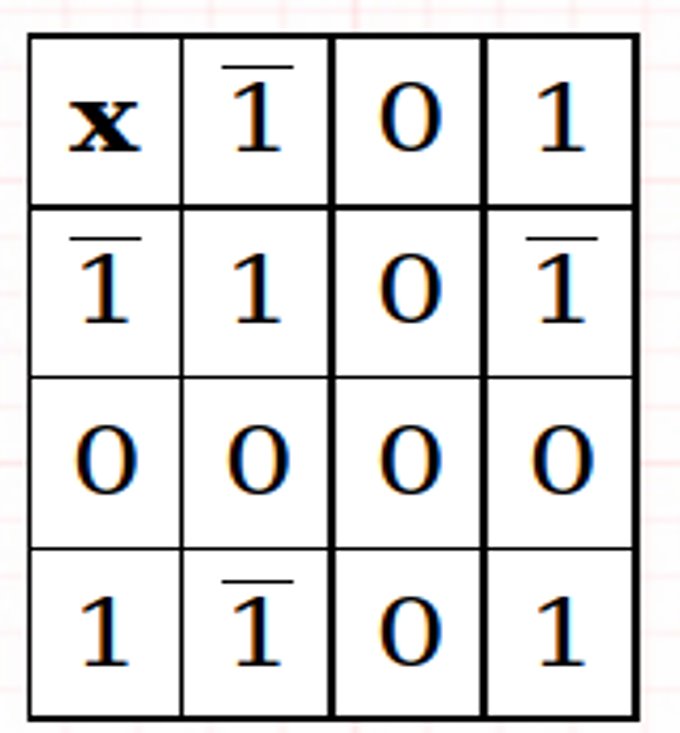
Ejemplos:
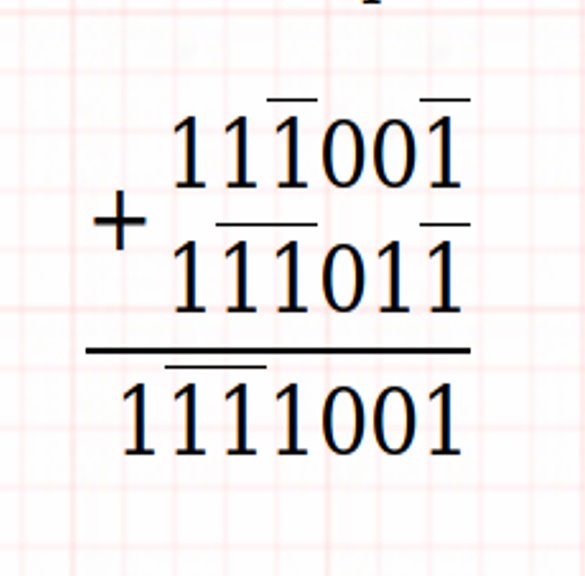
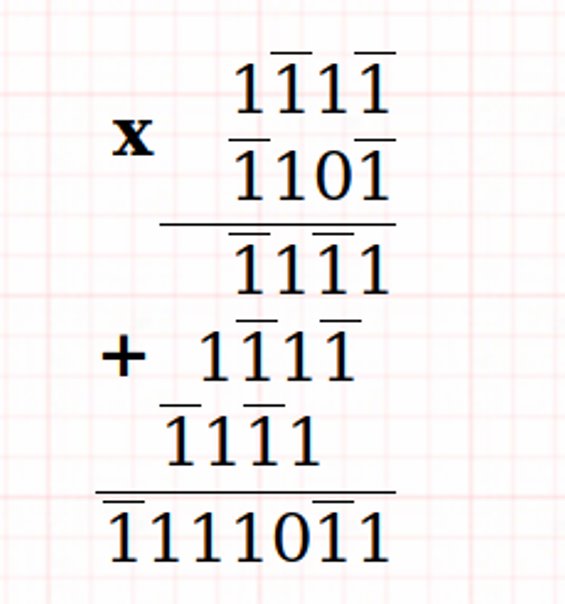
Circuitos combinacionales ternarios (compuertas ternarias)
Un circuito combinacional consta de variables de entrada, compuertas lógicas ternarias y variables de salida. La salida del circuito depende solo de la entrada actual. Las puertas lógicas aceptan señales de las variables de entrada y generan señales de salida. Este proceso transforma la información ternaria de
los datos de entrada dados a los datos de salida ternarios requeridos.
Como se mencionó anteriormente, podemos nombrar fácilmente una fracción significativa de los operadores booleanos (no, y, o, nand, ni, exclusivos o, equivalencia, implicación), sin embargo, no es razonable intentar nombrar todos menos una pequeña fracción de los posibles operadores ternarios. Consideraremos los siguientes circuitos ternarios:
Y (Min) : es natural extender el booleano y la función a una función ternaria declarando que el resultado es verdadero solo si ambas entradas son verdaderas, falso si alguna entrada es falsa y, de lo contrario, se desconoce.
Y circuito / tabla de verdad O (Máx.) : También es natural extender el booleano o la función a ternario al declarar que el resultado es verdadero si alguna entrada es verdadera, falsa solo si ambas entradas son falsas y, de lo contrario, se desconoce.
O circuito / tabla de verdad Consenso : en lógica booleana, el inverso de exclusivo o verdadero es verdadero cuando las dos entradas son iguales, y falso cuando son diferentes. Hay varias extensiones naturales de esta idea a la lógica ternaria. Uno de ellos es el consenso lógico de un conjunto de variables, que es verdadero si todos son verdaderos, falso si todos son falsos y de otro modo desconocido
Circuito de consenso / tabla de verdad Cualquiera : cuando el consenso requiera que ambas entradas estén de acuerdo antes de afirmar cualquier cosa menos desconocida, el operador aceptar cualquier cosa declara una conclusión desconocida solo si ambas entradas son desconocidas o están en desacuerdo activamente. De lo contrario, salta a una conclusión de cualquier entrada no desconocida disponible.
Cualquier circuito / tabla de verdad Incremento y decremento : en la lógica booleana, se puede considerar que el inversor aumenta o disminuye su argumento módulo 2. La lógica interna, las funciones de incremento y decremento del módulo 3 son bastante distintas de la inversión.
Circuito de incremento y decremento Síntesis, minimización y realización de funciones ternarias
Relaciones interrelacionadas en el sistema lógico ternario.
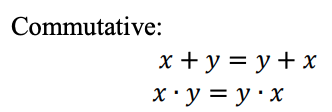
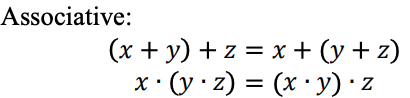
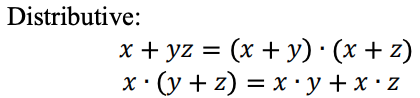
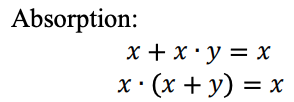
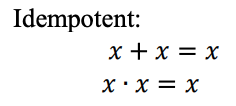
Una función lógica ternaria se puede representar como una expresión Max-Min. Las expresiones ternarias Max-Min se definen de la siguiente manera:
Variable : cualquier símbolo que tome valor del conjunto T ∈ {0,1,2} es una variable ternaria.
Literal : los literales son formas transformadas de una variable. Se usan para formar expresiones Max-Min.
En la literatura se usan comúnmente dos tipos de literales: literales de publicación 1-reducidos y literales de publicación 2-reducidos. Un literal de Post 1 reducido de una variable x se representa como x i , donde i ∈ {0,1,2}. Cuando x = i, entonces x i = 1, de lo contrario x i = 0. A continuación se muestran los literales Post reducidos en 1 de una variable.
Un literal de Post 2 reducido de una variable x se representa como x i , donde i ∈ {0,1,2}. Cuando x = i, entonces x i = 2, de lo contrario x i = 0. A continuación se muestran los literales Post reducidos en 2 de una variable. Este ejemplo hace uso de diferentes conjuntos de literales para formar expresiones Max-Min como se discutió anteriormente.
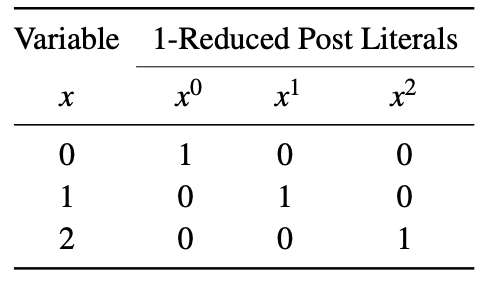
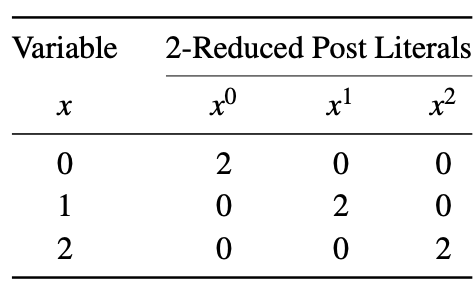
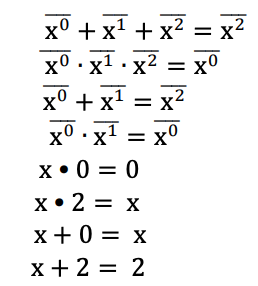
Minterm : cuando los literales de las variables de una función se combinan mediante la operación Min, el término se denomina minterm. Por ejemplo, para una función lógica ternaria de 3 variables F (x, y, z), xyz y xz son dos ejemplos de minterms.
Expresión Max-Min : cuando dos o más minterms se combinan mediante operaciones Max, la expresión se denomina expresión Max of minterms (Max-Min). Por ejemplo, para una función lógica ternaria de 3 variables F (x, y, z) = xy + yz + xyz es un ejemplo de una expresión Max-Min.
Cualquier función F (x, y, z) siempre se puede representar como
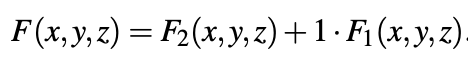
Tres métodos básicos para minimizar las funciones ternarias son:
- Manipulación de la expresión algebraica como en el álgebra booleana.
- El método tabular.
- Método de mapa K. ternario.
Para la implementación de circuitos ternarios, es necesario convertir la variable ternaria en variable unaria (utilizando la tabla 2-Post Literales reducidos).
Sumador ternario
Un circuito para la suma de dos números de 1 trit se denomina medio sumador. el circuito no considera un carry generado en la adición anterior. El proceso de adición en el sistema de lógica ternaria se muestra a continuación. Aquí A y B son dos entradas y suma (S) y carry (CARRY)
Son dos salidas.
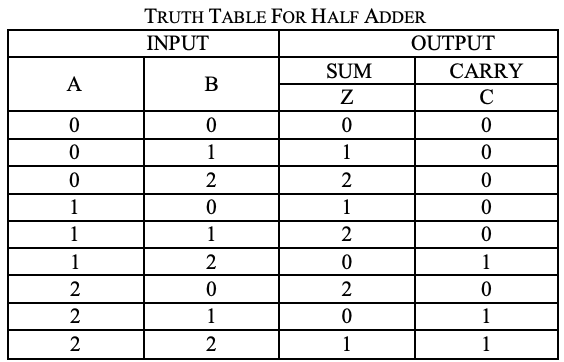
Análisis
Un mapa de karnaugh (K-map) se usa para representar la suma y la salida de transporte. Los mapas K son útiles para minimizar y optimizar los circuitos lógicos. Aquí se usa un K-map de 2 entradas. Como no es posible agrupar 2 y 1 ', la ecuación de salida es la siguiente.
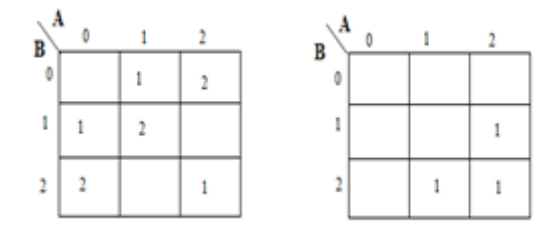
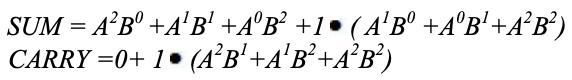
Implementación
Circuito sumador ternario / verilogmodule half_adder ( input [1:0] A, [1:0] B, output [1:0] sum, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; wire [1:0] c0, c1, c2, c3; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a2,b0,i0); andgate and_2(a1,b1,i1); andgate and_3(a0,b2,i2); // partial products orgate or_1(i0, i1, o0); orgate or_2(o0, i2, o1); // f1 andgate and_4(a1,b0,i3); andgate and_5(a0,b1,i4); andgate and_6(a2,b2,i5); // partial products orgate or_3(i3, i4, o2); orgate or_4(o2, i5, o3); // f2 andgate and_7(o3,temp,o4); // 1.f2 andgate andc_0(a2,b1,c0); andgate andc_1(a1,b2,c1); orgate orc_0(c0,c1,c2); orgate orc_1(c2,i5,c3); andgate andc_2(c3,temp,carry); // carry orgate or_5(o1, o4, sum); // sum endmodule
Sumador ternario completo
Al igual que con los medios sumadores, una etapa de un sumador ternario completo puede describirse mediante una tabla numérica que proporciona la suma SUMA y realiza CARRY en función de las tres entradas A, B, junto con el carry en C :
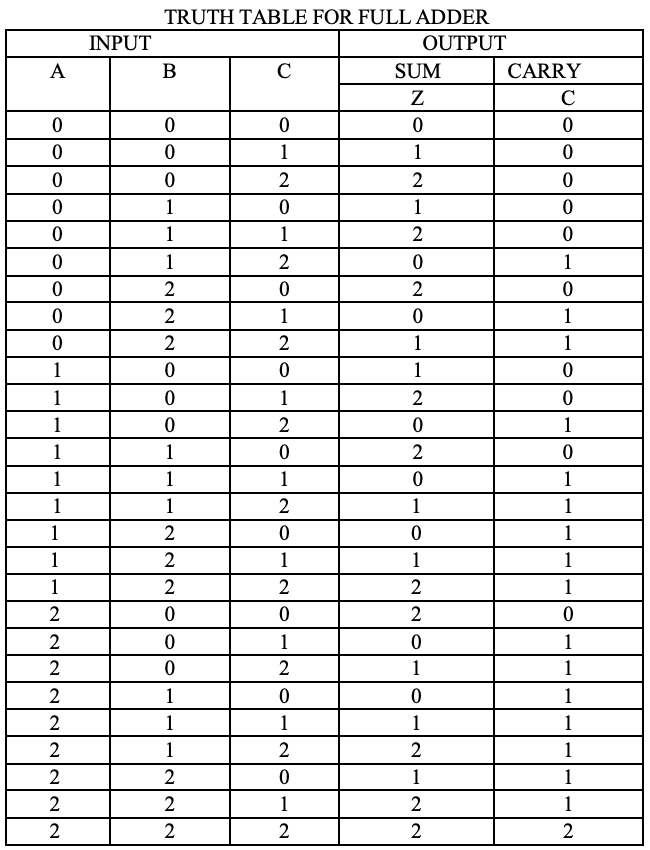
Análisis
Un mapa de karnaugh (K-map) se usa para representar la suma y la salida de transporte. Los mapas K son útiles para minimizar y optimizar los circuitos lógicos. Aquí se utiliza un mapa K de 3 entradas.
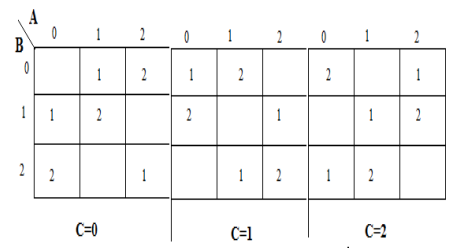
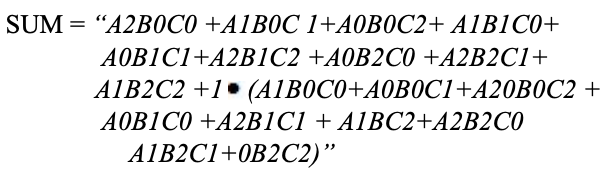
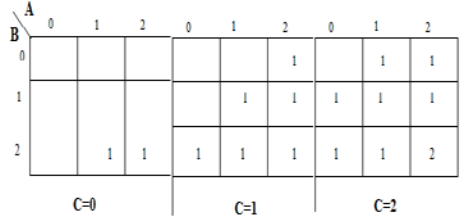
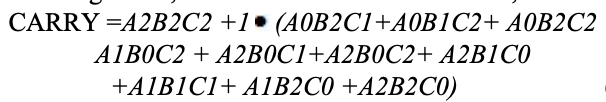
Implementación
Circuito sumador ternario / verilog module ternary_full_adder ( input [1:0] A, [1:0] B, [1:0] c_in, output [1:0] sum, [1:0] c_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b00; wire [1:0] a0, a1, a2, b0, b1, b2, a20; wire [1:0] i0, i1, i2, i3, i4; wire [1:0] i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] o0, o1, o2, o3, o4, o5, o6, o7, o8, o9; wire [1:0] c0, c1, c2; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16; wire [1:0] g0, g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15; mask mk_1(A, a0, a1, a2); mask mk_2(B, b0, b1, b2); mask mk_3(c_in, c0, c1, c2); andgate3 and3_1(a2,b0,c0, i0); andgate3 and3_2(a1,b0,c1, i1); andgate3 and3_3(a0,b0,c2, i2); andgate3 and3_4(a1,b1,c0, i3); andgate3 and3_5(a0,b1,c1, i4); andgate3 and3_6(a2,b1,c2, i5); andgate3 and3_7(a0,b2,c0, i6); andgate3 and3_8(a2,b2,c1, i7); andgate3 and3_9(a1,b2,c2, i8); andgate3 and3_10(a1,b0,c0, i9); andgate3 and3_11(a0,b0,c1, i10); orgate or__(a2, a0, a20); andgate3 and3_12(a20,b0,c2, i11); // note a20 andgate3 and3_13(a0,b1,c0, i12); andgate3 and3_14(a2,b1,c1, i13); andgate3 and3_15(a1,B,c2, i14); andgate3 and3_16(a2,b2,c0, i15); andgate3 and3_17(a1,b2,c1, i16); andgate3 and3_18(temp2,b2,c2, i17); orgate or_1(i9, i10, o0); orgate or_2(o0, i11, o1); orgate or_3(o1, i12, o2); orgate or_4(o2, i13, o3); orgate or_5(o3, i14, o4); orgate or_6(o4, i15, o5); orgate or_7(o5, i16, o6); orgate or_8(o6, i17, o7); andgate and_1(o7, temp1, o8); // 1.f2 orgate or_9(i0, i1, h0); orgate or_10(h0, i2, h1); orgate or_11(h1, i3, h2); orgate or_12(h2, i4, h3); orgate or_13(h3, i5, h4); orgate or_14(h4, i6, h5); orgate or_15(h5, i7, h6); orgate or_16(h6, i8, h7); orgate or_17_(h7, o8, sum); // sum // carry andgate3 and3_19(a2,b2,c2, t0); // f1 andgate3 and3_20(a0,b1,c2, t1); andgate3 and3_21(a0,b2,c2, t2); andgate3 and3_22(a0,b2,c1, t3); andgate3 and3_23(a1,b2,c0, t4); andgate3 and3_24(a2,b2,c0, t5); andgate3 and3_25(a1,b1,c1, t6); andgate3 and3_26(a1,b2,c1, t7); andgate3 and3_27(a1,b0,c2, t8); andgate3 and3_28(a1,b1,c2, t9); andgate3 and3_29(a1,b2,c2, t10); andgate3 and3_25_(a2,b0,c2, t11); andgate3 and3_26_(a2,b1,c2, t12); andgate3 and3_27_(a2,b0,c1, t13); andgate3 and3_28_(a2,b1,c1, t14); andgate3 and3_29_(a2,b2,c1, t15); andgate3 and3_9_(a2,b1,c0, t16); orgate or_17(t1, t2, g0); orgate or_18(g0, t3, g1); orgate or_19(g1, t4, g2); orgate or_20(g2, t5, g3); orgate or_21(g3, t6, g4); orgate or_22(g4, t7, g5); orgate or_23(g5, t8, g6); orgate or_24(g6, t9, g7); orgate or_25(g7, t10, g8); orgate or_21_(g8, t11, g9); orgate or_22_(g9, t12, g10); orgate or_23_(g10, t13, g11); orgate or_24_(g11, t14, g12); orgate or_25_(g12, t15, g13); orgate or_5_(g13, t16, g14); //f2 andgate and_2(g14, temp1, g15); // 1.f2 orgate or_26(g15, t0, c_out); // carry endmodule
Subtractor completo ternario
Ternary full-Subtractor es un circuito que resta dos entradas y préstamos anteriores. La tabla de verdad para Subtractor se muestra a continuación

Análisis e implementación del sustractor completo ternario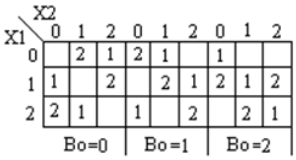
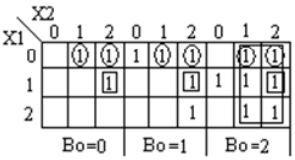
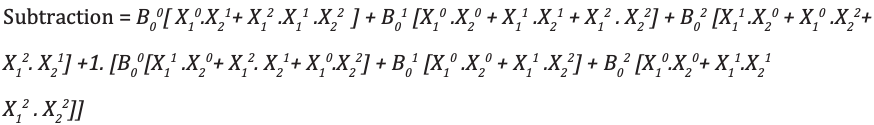
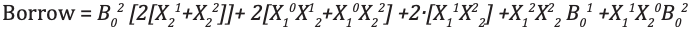
Código module full_subtractor( input [1:0] P, Q, b_in, output [1:0] diff, b_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b10; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] c0, c1, c2, c3; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7, h8, h9, h10, h11; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9; wire [1:0] p0, p1, p2; wire [1:0] q0, q1, q2; mask mk_1(P, p0, p1, p2); mask mk_2(Q, q0, q1, q2); mask mk_3(b_in, b0, b1, b2); andgate and_0(p0, q1, i0); andgate3 and3_0(p2, p1, q2, i1); orgate or_0(i0, i1, i2); andgate and_1(b0, i2, i3); // first expression andgate and_2(p0, q0, i4); andgate and_3(p1, q1, i5); andgate and_4(p2, q2, i6); orgate or_1(i4, i5, i7); orgate or_2(i7, i6, i8); andgate and_5(i8, b1, i9); // second expression andgate and_6(p1, q0, i10); andgate and_7(p0, q2, i11); andgate and_8(p2, q1, i12); orgate or_3(i10, i11, i13); orgate or_4(i13, i12, i14); andgate and_9(i14, b2, i15); // third expression orgate or_5(i3, i9, i16); orgate or_6(i16, i15, c0); //f1 orgate or_7(i10, i12, t0); orgate or_8(t0, i11, t1); andgate and_10(t1, b0, t2); // 1 expression andgate and_11(p1, q2, i17); orgate or_9(i4, i17, t3); andgate and_12(t3, b1, t4); // 1- expression orgate or_10(i4, i5, t5); orgate or_11(t5, i6, t6); andgate and_12_(t6, b2, t7); // 1-- expression orgate or_12(t2, t4, t8); orgate or_13(t8, t7, t9); andgate and_13(t9, temp1, c1); orgate or_14(c0, c1, diff); // difference orgate or_15(q1, q2, h0); andgate and_14(h0, temp2, h1); andgate and_15(h1, b2, h3); // 1 b orgate or_16(i0, i11, h4); andgate and_16(h4, temp2, h5); // 1- b andgate and_17(i17, temp2, h6); // 1-- b andgate3 and3_1(p2, q2, b1, h7); // 1--- b andgate3 and3_2(p1, q0, b2, h8); // 1---- b orgate or_17(h3, h5, h9); orgate or_18(h9, h6, h10); orgate or_19(h10, h7, h11); orgate or_20(h11, h8, b_out); // borrow endmodule
Ondulación Ternaria
El sumador Ripple-carry (RCA) es un circuito bien conocido para realizar la suma de dos números mediante la suma de ternarios sumadores completos. Un RCA ternario es bastante similar a su contraparte binaria. Un medio sumador ternario se emplea para agregar los dígitos ternarios menos significativos. El resto se resume en Ternary Full Adders. Como se mencionó anteriormente, Ternary Full Adder agrega tres variables de entrada Ternary.
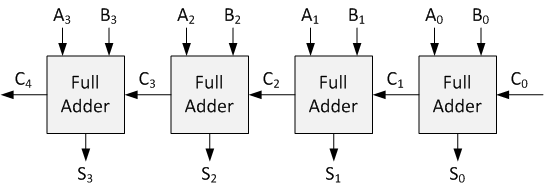
Implementación
código verilog: sumador de transporte de ondas ternarias module ternary_ripple_adder ( input [15:0] input1 , input [15:0] input2 , output [15:0] out , output [1:0] overflow_trit ); wire [15:0] carry ; reg tem; assign carry[0] = tem; assign carry[1] = tem; always @(input1, input2) begin tem <= 1'b0; end generate genvar i; for (i = 0; i <= 12; i=i+2) begin full_add af({input1[i+1],input1[i]}, {input2[i+1],input2[i]}, {carry[i+1],carry[i]}, {out[i+1], out[i]}, {carry[i+3],carry[i+2]}); end full_add af({input1[15],input1[14]}, {input2[15],input2[14]}, {carry[15],carry[14]}, {out[15], out[14]}, overflow_trit); endgenerate endmodule
Comparadores ternarios
Circuito comparador ternario camper dos entradas X 1 , X 2 y en consecuencia genera salida como X 1 = X 2 , X 1 > X 2 , X 1 <X 2 . La tabla de verdad para un comparador ternario se muestra a continuación
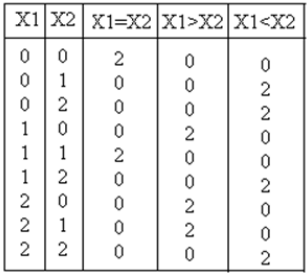
Análisis e implementaciónLa ecuación de salida para X 1 = X 2 , X 1 > X 2 , X 1 <X 2 son:
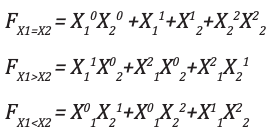
Los k-mapas correspondientes se muestran a continuación

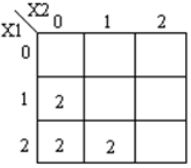
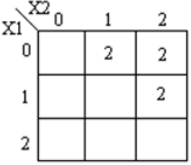
Código module ternary_comparators ( input [1:0] x1, x2, output [1:0] f1, f2, f3 ); wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7; wire [1:0] h0, h1, h2, h3, h4, h5; wire [1:0] x10, x11, x12; wire [1:0] x20, x21, x22; mask mk_1(x1, x10, x11, x12); mask mk_2(x2, x20, x21, x22); andgate and_0(x10, x20, t0); andgate and_1(x22, x22, t1); orgate or_0(t0, t1, h0); orgate or_1(h0, x11, h1); orgate or_2(h1, x21, f1); // x1 == x2 andgate and_2(x11, x20, t2); andgate and_3(x12, x20, t3); andgate and_4(x12, x21, t4); orgate or_3(t2, t3, h3); orgate or_4(h3, t4, f2); // x1>x2 andgate and_5(x10, x21, t5); andgate and_6(x10, x22, t6); andgate and_7(x11, x22, t7); orgate or_5(t5, t6, h4); orgate or_6(h4, t7, f3); // x1<X2 endmodule
Multiplicador ternario
El multiplicador ternario es un circuito que multiplica dos números de entrada y genera el producto correspondiente. La tabla de verdad para este circuito se muestra a continuación:
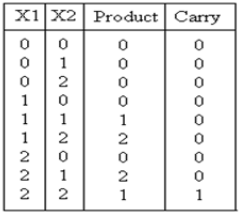
Análisis e implementaciónLa expresión resultante para el producto y el carry se muestran:
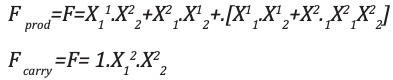
Se muestran los mapas K correspondientes:
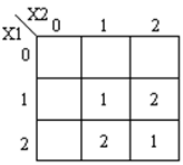
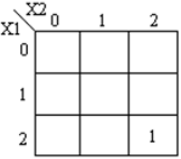
Código module ternary_multiplier ( input [1:0] A, [1:0] B, output [1:0] product, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a1,b2,i0); andgate and_2(a2,b1,i1); orgate or_1(i0, i1, o0); // f1 andgate and_4(a1,b1,i3); andgate and_5(a2,b2,i4); orgate or_3(i3, i4, o2); andgate and_3(temp,o2,o3); orgate or_4(o3, o0, product); // product andgate andc_0(a2,b2,o4); andgate andc_1(temp,o4,carry); // carry endmodule
Multiplexores ternarios y demultiplexores
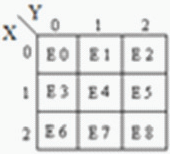
El multiplexor es un circuito que tiene múltiples entradas y una sola salida. También se conoce como decodificador. La función de salida del multiplexor está determinada por el número de líneas de función. Así por 2 trit
multiplexor la salida será 3 2 = 9 y dos serán las líneas de selección de función. Multiplexor, es decir, función
La lógica de selección selecciona 1 de 9 funciones como salida. La lógica de selección de funciones se implementa utilizando puertas lógicas. La ecuación de salida de la lógica de selección de funciones es:
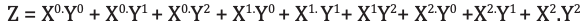
Análisis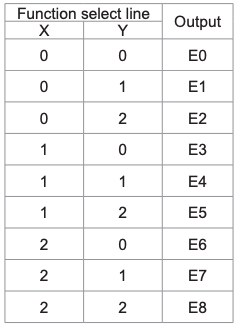
El demultiplexor también se conoce como codificador. Su funcionalidad es inversa a la del multiplexor. Acepta la entrada única y la distribuye en varias salidas.
Pestillo ternario simple d
Aunque el diseño de circuitos que implementan lógica ternaria combinatoria es sencillo, el diseño de un elemento de memoria ternario simple y robusto (es decir, pestillo) adecuado para la implementación de circuitos integrados (IC) ha sido un desafío. Sin embargo, se puede obtener un cierre ternario simple reemplazando las compuertas binarias NOR o NAND utilizadas con las compuertas ternarias T_NOR o T_NAND correspondientes.
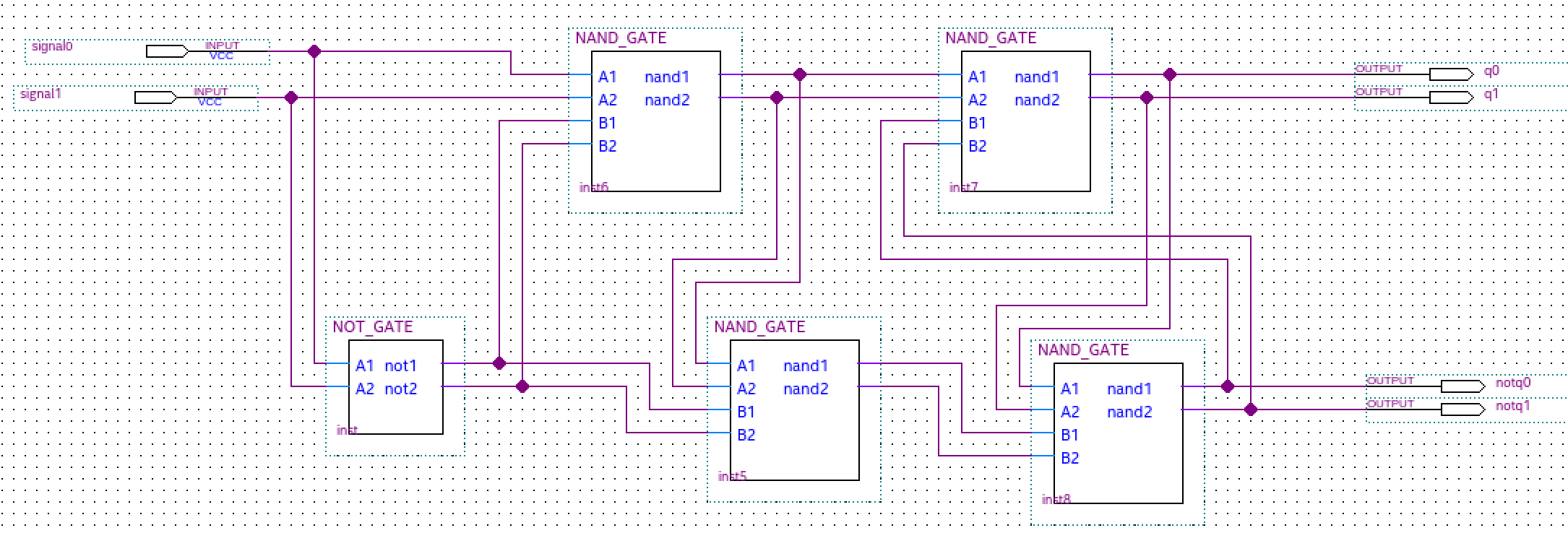
Flip-Flap-Flop Ternario D simple
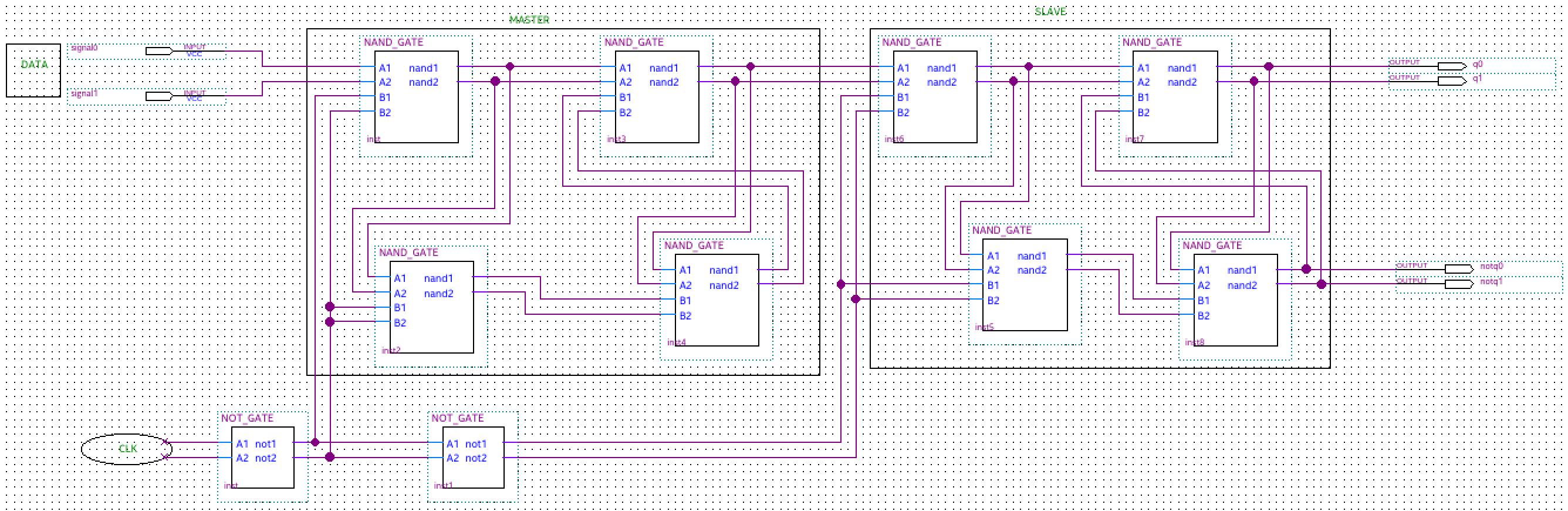
El Flip-Flap-Flop (FFF) ternario D maestro esclavo (MS) se realiza en función de los pestillos D ternarios. Esto es similar a la forma en que el binario D Flip-Flop (FF) se realiza utilizando pestillos binarios D. El diagrama lógico y la descripción de la operación del flip-flop binario D de MS son bien conocidos. Para implementar el MS ternary D FFF , reemplazamos los pestillos D binarios con pestillos D ternarios (realizados con compuertas ternarias mínimas negadas de dos entradas - NAND) y los inversores binarios con inversores ternarios simples (STI). Se muestran las tablas de verdad tanto para los circuitos NAND ternarios como para los circuitos STI ternarios.
Tabla de verdad para circuitos nand y sti Para MS ternary D FFF con reloj binario, los datos son ternarios (lógica 0, 1 y 2) y el reloj es binario (bajo y alto - en nuestro
implementación, lógica 0 y 2). El MS ternario D FFF con
El reloj binario puede leer los datos cuando el reloj pasa de bajo a
alto (borde positivo) o de alto a bajo (borde negativo), dependiendo
sobre el número de ITS.
Las entradas del ternario D FFF son Data y Clk, y las salidas son Q y Not_Q. La señal de reloj es binaria y los niveles lógicos se denotan 0 y 2, para mantener la correspondencia con la implementación eléctrica.
Unidad aritmética y lógica ternaria de 1 bit (T-ALU)
La Unidad de lógica aritmética ternaria (ALU) es un circuito digital utilizado para realizar operaciones aritméticas y lógicas. Representa el bloque de construcción fundamental de la Unidad Central de Procesamiento (CPU) de una computadora ternaria. ALU realiza operaciones aritméticas como suma, resta, multiplicación y comparación de operaciones lógicas, NAND, NOR, NOT, AND y OR. A continuación se muestra una arquitectura primitiva de una ALU de 1 trit
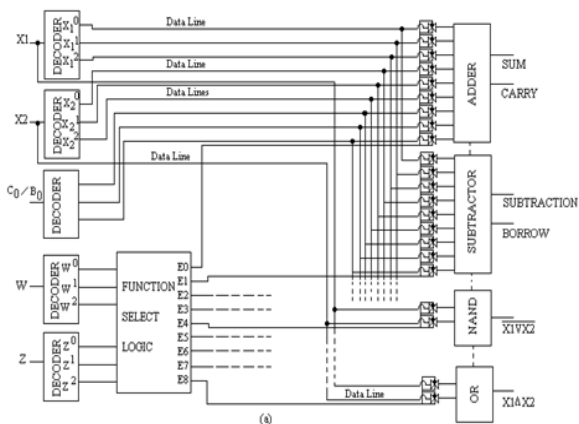
Tabla de verdad y funcionamiento para T-ALU Los componentes básicos de ALU son decodificadores, lógica de selección de funciones (multiplexor), puerta de transmisión y módulos de procesamiento separados. La lógica de selección de funciones selecciona 1 de las 9 funciones enumeradas dependiendo del estado lógico en las líneas de selección de funciones W y Z.
Las líneas de salida de la lógica de selección están conectadas a TG (puerta ternaria) asociada con cada módulo. Cualquier módulo se selecciona solo cuando el TG asociado está habilitado; de lo contrario, está aislado de las líneas de datos. Por ejemplo, si la entrada de las líneas de selección W y Z = 0, la salida E 0 de la lógica de selección es alta (2) mientras que E 1 , a E 8 es baja (0), entonces, el TG asociado con el módulo sumador permitirá los datos
líneas que se conectarán a los módulos sumadores mientras que otros módulos están aislados de las líneas de datos.
Finalmente, al poner en cascada n / 2 trit ALU cortes, se puede formar un n trit ALU.