Los tipos de fusión funcionan según este principio:

1. Se buscan submatrices ordenadas (como opción, se forman).
2. Las submatrices ordenadas se concatenan en una submatriz ordenada común.

Por sí mismo, cualquier subconjunto ordenado dentro de la matriz no tiene mucho valor. Pero si en una matriz encontramos dos subarreglos ordenados, entonces este es un asunto completamente diferente. El hecho es que puede fusionarlos muy rápidamente y a un costo mínimo, para formar un subconjunto ordenado general a partir de un par de subconjuntos ordenados.



Como puede ver, combinar dos matrices ordenadas en una no es fácil, pero sí muy simple. Debe moverse simultáneamente en ambas matrices de izquierda a derecha y comparar los siguientes pares de elementos de ambas matrices. El elemento más pequeño se envía a la caldera común. Cuando los elementos terminan en una de las matrices, los elementos restantes de la otra matriz simplemente se transfieren a la lista principal en orden.

Esta es la sal de los algoritmos de esta clase. Inicialmente, una matriz aleatoria se puede dividir en muchas pequeñas subarreglas ordenadas. En la fusión por pares, el número de subarreglos ordenados disminuye, la longitud de cada uno de ellos aumenta. En el último paso, la matriz consta de solo dos subarreglos ordenados que se fusionan en una sola estructura ordenada.


El autor de este concepto es John von Neumann. A veces hay una controvertida afirmación de que se le ocurrió clasificar mientras trabajaba en el proyecto de Manhattan, ya que se enfrentó a la tarea de proporcionar cálculos efectivos de una gran cantidad de datos estadísticos en el desarrollo de una bomba nuclear. Es difícil evaluar la credibilidad de esta versión, ya que su primer trabajo de clasificación por fusión data de 1948, y la creación de la bomba se completó 3 años antes. Sin embargo, qué tipo de clasificación atómica hay, echemos un vistazo.

Fusión natural de Neumann

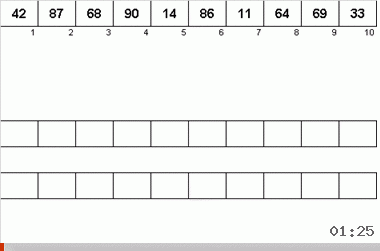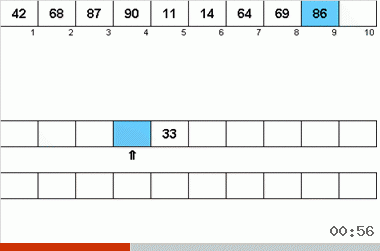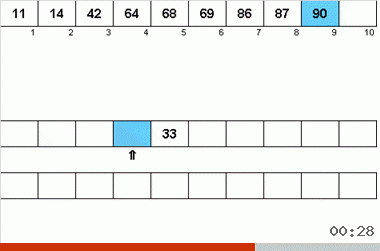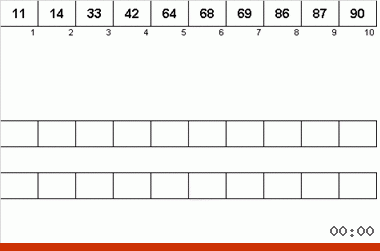
El algoritmo de Neyman fue influenciado por las características de diseño de las computadoras de los años 40. Se veía así:

1. En total, se utilizan tres cintas magnéticas, la principal, en la que se graban datos no clasificados y dos datos auxiliares.
2. Los datos se leen secuencialmente desde la cinta principal.
3. Si bien los datos leídos secuencialmente son una submatriz ordenada, se copian en una de las cintas auxiliares.
4. Tan pronto como se completa la siguiente subcadena ordenada (es decir, se encuentra un elemento más pequeño que el anterior en la cinta principal), se coloca un puntero en la cinta auxiliar (final de la submatriz) y se cambia a otra cinta auxiliar.
5. Los puntos 2-4 se repiten nuevamente, solo los datos se transfieren a otra cinta auxiliar. Al final del siguiente subarreglo ordenado, la cinta principal alterna alternativamente a una cinta auxiliar, luego a otra.
6. Cuando se han leído todos los datos de la cinta principal, tiene lugar el procesamiento de las cintas auxiliares.
7. Ambas cintas auxiliares leen los datos a su vez.
8. En este caso, los siguientes datos de dos cintas se comparan entre sí. Según los resultados de la comparación, el elemento más pequeño del par se graba en la cinta principal.
9. Dado que los límites de las matrices en las cintas auxiliares están marcados con punteros, la lectura y la comparación solo se producen dentro de las subarreglas ordenadas.
10. Si en una de las cintas auxiliares los elementos de la siguiente submatriz han terminado, entonces de la cinta restante, el resto de la submatriz simplemente se transfiere a la cinta principal.
11. Repetimos todo el proceso nuevamente hasta que los datos en la cinta principal sean una matriz completamente ordenada.

La ordenación de Neumann es un algoritmo adaptativo: no solo corrige las piezas ordenadas de la matriz, sino que, en primer lugar, intenta aumentarlas, de modo que, sobre la base de subarreglos ordenados alargados para formar subarreglos ordenados aún más largos. Por lo tanto, también se llama clasificación de fusión adaptativa .

La complejidad de este algoritmo es modesta - O ( n ² ), y, sin embargo, para los pioneros de la computación en tubo esto fue un gran avance.

En el ejemplo de este primer tipo de fusión, un inconveniente de esta clase de algoritmos ya es visible: el costo de la memoria adicional. En este sentido, casi todas las clasificaciones de fusión requieren adicionalmente O ( n ), sin embargo, las excepciones elegantes son raras.

Fusión directa Bowes-Nelson

Estrictamente hablando, el algoritmo Bowes-Nelson es una red de clasificación, no de clasificación. En el proceso, la matriz y todas sus submatrices se dividen por la mitad y nada impide que todas estas mitades se procesen en paralelo en todas las etapas. Sin embargo, también se puede representar en forma de clasificación. Y también abordaremos el tema de la clasificación de redes.

1. La matriz se divide por la mitad, en las mitades izquierda y derecha.
2. Los elementos se dividen en grupos.
3. En la primera iteración, estos son los dos elementos (el primer elemento de la mitad izquierda + el primer elemento de la mitad derecha, el segundo elemento de la mitad izquierda + el segundo elemento de la mitad derecha, etc.), en la segunda iteración, los cuatro elementos (1- 2º y 2º elementos de la mitad izquierda + 1º y 2º elementos de la mitad derecha, 3º y 4º elementos de la mitad izquierda + 3º y 4º elementos de la mitad derecha, etc.), en el tercero - ochos, etc.
4. Los elementos de cada grupo de la mitad izquierda son subarreglos ordenados, los elementos de cada grupo de la mitad derecha también son subarreglos ordenados.
5. Combinar las submatrices ordenadas del párrafo anterior.
6. Volvemos al punto 1. El ciclo continúa hasta que los tamaños de los grupos son más pequeños que el tamaño de la matriz.

Puede parecer que se requiere memoria adicional aquí. Pero no! Para una percepción más comprensible en la animación, las mitades izquierda y derecha de la matriz se ubican una sobre la otra, de modo que la posición relativa de las submatrices comparadas es más obvia. Sin embargo, debido a la estricta bisección, es posible un algoritmo en el que se realicen todas las comparaciones e intercambios, sin involucrar recursos adicionales de la memoria. Lo cual es muy inusual para la clasificación por fusión.

def bose_nelson(data): m = 1 while m < len(data): j = 0 while j + m < len(data): bose_nelson_merge(j, m, m) j = j + m + m m = m + m return data def bose_nelson_merge(j, r, m): if j + r < len(data): if m == 1: if data[j] > data[j + r]: data[j], data[j + r] = data[j + r], data[j] else: m = m // 2 bose_nelson_merge(j, r, m) if j + r + m < len(data): bose_nelson_merge(j + m, r, m) bose_nelson_merge(j + m, r - m, m) return data 

Hay algo en todas las fusiones de clasificación que los hace similares a la bomba de hidrógeno. Primero se produce la división, luego la síntesis.

Referencias

Fusionar / Fusionar

Artículos de la serie:

• Aplicación Excel AlgoLab.xlsm
• Clases de intercambio
• Clases de inserción
• Ordenar por selección
• Combinar clasificaciones
  • Fusión equilibrada de arriba hacia abajo y de abajo hacia arriba
  • Orden de fusión multifase
  • Ordenar fusión en cascada
  • Orden de fusión oscilante
  • Clasificaciones roscadas e inmiscibles
  • Combinar clasificación de clasificación
• Ordenar por distribución
• Clasificación híbrida

Las dos clasificaciones mencionadas en el artículo de hoy están ahora disponibles en la aplicación AlgoLab (para aquellos que estudian algoritmos usando esta aplicación de Excel, actualicen el archivo). Y en solo un par de días, con el lanzamiento de una próxima secuela de fusión, estarán disponibles varios algoritmos más de esta clase.

Hay una restricción para la clasificación de Bowes-Nelson: el tamaño de la matriz debe ser una potencia de dos. Si no se cumple esta condición, la macro recortará la matriz a un tamaño adecuado.

Este artículo fue escrito con el apoyo de EDISON Software, una compañía que escribe software de reconstrucción 3D y está desarrollando sofisticados equipos de medición .