Después del verdadero auge de los juegos de mesa de finales de los años 00, la familia dejó varias cajas con juegos. Uno de ellos es el juego "Hare and Hedgehog" en la versión original en alemán. Un juego para varios jugadores, en el que se minimiza el elemento de aleatoriedad, y el cálculo sobrio y la capacidad del jugador de "mirar hacia adelante" en varios pasos gana.
Mis frecuentes derrotas en el juego me llevaron a escribir "inteligencia" en la computadora para elegir el mejor movimiento. Inteligencia, idealmente capaz de luchar contra el gran maestro de la Liebre y el Erizo (y qué, té, no ajedrez, el juego será más fácil). El resto del artículo describe el proceso de desarrollo, la lógica de IA y un enlace a la fuente.
Reglas del juego Hare and Hedgehog
En el campo de juego de 65 celdas hay varias fichas de jugador, de 2 a 6 participantes (mi dibujo, no canónico, miradas, por supuesto, más o menos):
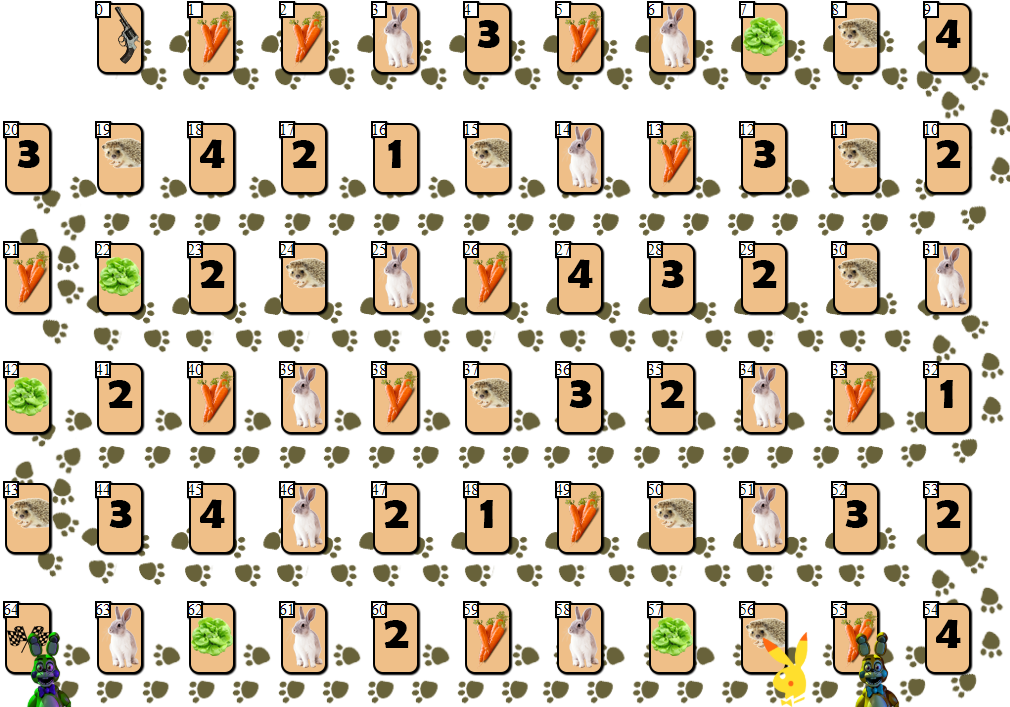
Además de las celdas con índices 0 (inicio) y 64 (finalización), solo se puede colocar un jugador en cada una de las celdas. El objetivo de cada jugador es avanzar hacia la celda de meta, por delante de sus rivales.
El "combustible" para avanzar es la zanahoria, la "
moneda " del juego. Al principio, cada jugador recibe 68 zanahorias, que él da (y a veces recibe) a medida que se mueve.
Además de las zanahorias, al principio el jugador recibe 3 tarjetas de ensalada. La ensalada es un "artefacto" especial que un jugador debe
eliminar antes del final. Deshacerse de la lechuga (y esto solo se puede hacer en una jaula especial de lechuga, como esta:

), el jugador, incluido, recibe zanahorias adicionales. Antes de eso, omitiendo tu movimiento. Cuantos más jugadores enfrente de la ensalada salgan de la carta, más zanahorias recibirá ese jugador: 10 x (la posición del jugador en el campo en relación con otros jugadores). Es decir, el jugador parado en el campo en segundo lugar recibirá 20 zanahorias, dejando la jaula de la ensalada.
Las celdas con los números 1 a 4 pueden traer varias decenas de zanahorias si la posición del jugador coincide con el número en la celda (1 a 4, la celda con el número 1 también es adecuada para las posiciones 4 y 6 en el campo), por analogía con la celda de lechuga.
El jugador puede omitir el movimiento, permanecer en la jaula con la imagen de zanahorias y recibir o dar 10 zanahorias para esta acción. ¿Por qué un jugador debe dar "combustible"? El hecho es que un jugador puede terminar teniendo solo 10 zanahorias después de su movimiento final (20 si termina segundo, 30 si termina tercero, etc.).
Finalmente, el jugador puede obtener 10 x N zanahorias dando N pasos en el erizo
libre más cercano (si el erizo más cercano está ocupado, tal movimiento es imposible).
El costo de avanzar se calcula no proporcionalmente al número de movimientos, de acuerdo con la fórmula (con redondeo):
fracN+N22 ,
donde N es el número de pasos hacia adelante.
Entonces, para avanzar una celda, el jugador da 1 zanahoria, 3 zanahorias para 2 celdas, 6 zanahorias para 3 celdas, 10 para 4, ..., 210 zanahorias para mover 20 celdas hacia adelante.
La última celda, la celda con la imagen de una liebre, introduce un elemento de aleatoriedad en el juego. Habiéndose parado en una jaula con una liebre, el jugador roba una carta especial de la pila, después de lo cual se realiza alguna acción. Dependiendo de la tarjeta y la situación del juego, el jugador puede perder algunas zanahorias, obtener zanahorias adicionales o saltar un turno. Vale la pena señalar que entre las cartas con "efectos" hay varios escenarios negativos más para el jugador, lo que alienta al juego a ser cuidadoso y calculado.
Implementación sin IA
En la primera implementación, que luego se convertirá en la base para el desarrollo del "intelecto" del juego, me limité a la opción en la que cada jugador hace un movimiento: una persona.
Decidí implementar el juego como cliente, un sitio web estático de una página, cuya "lógica" se implementa en JS y el servidor, la aplicación API WEB. El servidor está escrito en .NET Core 2.1 y produce un artefacto de ensamblaje: un archivo dll, que se puede ejecutar en Windows / Linux / Mac OS.
La "lógica" de la parte del cliente se minimiza (así como la UX, ya que la GUI es puramente utilitaria). Por ejemplo, el cliente web no realiza la verificación por sí mismo para ver si las reglas solicitadas por el jugador son aceptables. Esta verificación se realiza en el servidor. El servidor le dice al cliente qué movimientos puede hacer el jugador desde la posición actual del juego.
El servidor es una
máquina clásica de
Moore . La lógica del servidor carece de conceptos como "cliente conectado", "sesión de juego", etc.
Todo lo que el servidor hace es procesar el comando recibido (HTTP POST). El
patrón de "comando" se implementa en el servidor. El cliente puede solicitar la ejecución de uno de los siguientes comandos:
- comenzar un nuevo juego, es decir "Colocar" fichas del número especificado de jugadores en un tablero "limpio"
- hacer el movimiento indicado en el comando
Para el segundo equipo, el cliente envía al servidor la posición actual del juego (objeto de la clase Disposición), es decir, una descripción de la siguiente forma:
- posición, número de zanahorias y lechuga para cada liebre, más un campo booleano adicional que indica que a la liebre le falta su turno
- índice de la liebre haciendo el movimiento.
El servidor no necesita enviar información adicional, por ejemplo, información sobre el campo de juego. Al igual que para grabar un boceto de ajedrez, no es necesario pintar la disposición de las celdas en blanco y negro en el tablero; esta información se toma como una constante.
En respuesta, el servidor indica si el comando se completó correctamente. Técnicamente, un cliente puede, por ejemplo, solicitar un movimiento no válido. O intente crear un nuevo juego para un solo participante, lo que obviamente no tiene sentido.
Si el equipo tiene éxito, la respuesta contendrá una nueva
posición de juego, así como una lista de movimientos que puede realizar el próximo jugador en la cola (actual para la nueva posición).
Además de esto, la respuesta del servidor contiene algunos campos de servicio. Por ejemplo, el texto de una carta de una liebre "sacada" por un jugador en un paso en la jaula correspondiente.
Turno de jugador
El turno del jugador está codificado como un entero:
- 0, si el jugador se ve obligado a permanecer en la celda actual,
1, 2, ... N para 1, ... N da un paso adelante, - -1, -2, ... -M para mover 1 ... M celdas de vuelta al erizo libre más cercano,
- 1001, 1002: códigos especiales para el jugador que decidió quedarse en la celda de zanahoria y recibir (1001) o dar (1002) 10 zanahorias por esto.
Implementación de software
El servidor recibe el JSON del comando solicitado, lo analiza en una de las clases de solicitud correspondientes y realiza la acción solicitada.
Si el cliente (jugador) solicitó hacer un movimiento con el código CMD desde la posición (POS) transferida al equipo, el servidor realiza las siguientes acciones:
- comprueba si tal movimiento es posible
- crea una nueva posición desde la actual, aplicando las modificaciones correspondientes,
obtiene muchos movimientos posibles para una nueva posición. Permíteme recordarte que el índice del jugador que realiza el movimiento ya está incluido en el objeto que describe la posición , - devuelve al cliente una respuesta con una nueva posición, posibles movimientos o el indicador de éxito igual a falso, y una descripción del error.
La lógica de verificar la admisibilidad del movimiento solicitado (CMD) y construir una nueva posición resultó estar un poco más cerca de lo que quisiéramos. Con esta lógica, el método para encontrar movimientos aceptables tiene algo en común. Toda esta funcionalidad es implementada por la clase TurnChecker.
A la entrada de los métodos de verificación / ejecución, TurnChecker recibe un objeto de la clase de la posición del juego (Disposición). El objeto Disposition contiene una matriz de datos del jugador (Haze [] hazes), el índice del jugador que realiza el movimiento + alguna información de servicio que se completa durante la operación del objeto TurnChecker.
El campo de juego describe la clase FieldMap, que se implementa como un
singleton . La clase contiene una matriz de celdas + cierta información general utilizada para simplificar / acelerar los cálculos posteriores.
Consideraciones de rendimientoEn la implementación de la clase TurnChecker, traté de evitar los bucles tanto como sea posible. El hecho es que los métodos para obtener el conjunto de movimientos permitidos / ejecución de un movimiento se llamarán miles (decenas de miles) de veces durante el procedimiento de búsqueda de un movimiento cuasi óptimo.
Entonces, por ejemplo, calculo cuántas celdas puede avanzar un jugador con N zanahorias, usando la fórmula:
return ((int)Math.Pow(8 * N + 1, 0.5) - 1) / 2;
Verificando si la celda i está ocupada por uno de los jugadores, no reviso la lista de jugadores (ya que esta acción probablemente tendrá que realizarse muchas veces), pero me dirijo al diccionario del formulario
[cell_index, busy_cage_ flag] completado por adelantado.
Al verificar si la celda hedgehog especificada es la más cercana (detrás) a la celda actual ocupada por el jugador, también comparo la posición solicitada con un valor de un diccionario de la forma
[cell_index ,arest_back_dezh] _index] - información estática.
Implementación con IA
Se agrega un comando a la lista de comandos procesados por el servidor: ejecute un movimiento cuasi óptimo seleccionado por el programa. Este equipo es una pequeña modificación del comando "movimiento del jugador", del cual, de hecho, el campo de movimiento (
CMD ) se ha eliminado.
La primera decisión que viene a la mente es utilizar la heurística para seleccionar el "mejor movimiento posible". Por analogía con el ajedrez, podemos evaluar cada una de las posiciones de juego obtenidas con nuestro movimiento estableciendo algún tipo de calificación para esta posición.
Evaluación de posición heurística
Por ejemplo, en el ajedrez, es bastante simple hacer una evaluación (sin subir a la naturaleza de las aperturas): como mínimo, puede calcular el "costo" total de las piezas tomando el valor de caballero / alfil por 3 peones, el valor de la torre de 5 peones, la reina 9 y el rey
int Peones
MaxValue . Es fácil mejorar la estimación, por ejemplo, añadiéndole (con un factor de corrección - factor / exponente u otra función):
- el número de movimientos posibles desde la posición actual,
- proporción de amenazas a figuras enemigas / amenazas del enemigo.
Se da una evaluación especial a la posición del tapete:
int.MaxValue , si el jaque mate puso la computadora,
int.MinValue si el jaque mate puso a la persona.
Si le ordena al procesador de ajedrez que elija el siguiente movimiento, guiado solo por dicha evaluación, el procesador probablemente elegirá no los peores movimientos. En particular:
- No pierdas la oportunidad de tomar una pieza más grande o un jaque mate,
- lo más probable es que no conduzca las figuras en las esquinas,
- No vuelve a poner la cifra bajo ataque (dada la cantidad de amenazas en la evaluación).
Por supuesto, tales movimientos de la computadora no le dejarán una posibilidad de éxito con un oponente que haga sus movimientos en el más mínimo sentido. La computadora ignorará cualquiera de los enchufes. Además, probablemente no dude en cambiar incluso a la reina por un peón.
Sin embargo, el algoritmo para la evaluación heurística de la posición de juego actual en el ajedrez (sin reclamar los laureles del programa campeón) es bastante transparente. No se puede decir sobre el juego Hare and Hedgehog.
En el caso general, en el juego The Hare and the Hedgehog, una máxima bastante borrosa funciona: "
es mejor ir más lejos con más zanahorias y menos lechuga ". Sin embargo, no todo es tan sencillo. Digamos, si un jugador tiene 1 carta de ensalada en el medio del juego, esta opción puede ser bastante buena. Pero el jugador parado en la línea de meta con una tarjeta de ensalada obviamente estará en una situación perdedora. Además del algoritmo de evaluación, también me gustaría poder "espiar" un paso más allá, así como las amenazas a las piezas pueden contarse en una evaluación heurística de una posición de ajedrez. Por ejemplo, vale la pena considerar la bonificación de las zanahorias recibidas por un jugador que sale de la celda de lechuga / celda de posición (1 ... 4), teniendo en cuenta el número de jugadores en el frente.
Deducí la calificación final como una función:
E = Ks * S + Kc * C + Kp * P,
donde S, C, P son calificaciones calculadas usando tarjetas de ensalada (S) y zanahorias © en las manos del jugador, P son las calificaciones otorgadas al jugador por la distancia recorrida.
Ks, Kc, Kp son los factores de corrección correspondientes (se discutirán más adelante).
La forma más fácil es determinar la marca
del camino recorrido :
P = i * 3, donde i es el índice de la celda en la que se encuentra el jugador.
La calificación C (zanahorias) ya es más difícil.
Para obtener un valor C específico, elijo una de las 3 funciones
C0,C1,C2 de un argumento (el número de zanahorias en las manos). El índice de la función C ([0, 1, 2]) está determinado por la posición relativa del jugador en el campo de juego:
- [0] si el jugador ha completado menos de la mitad del campo de juego,
- [2] si un jugador tiene suficientes zanahorias (mb, incluso abundantes) para terminar,
- [1] en otros casos.
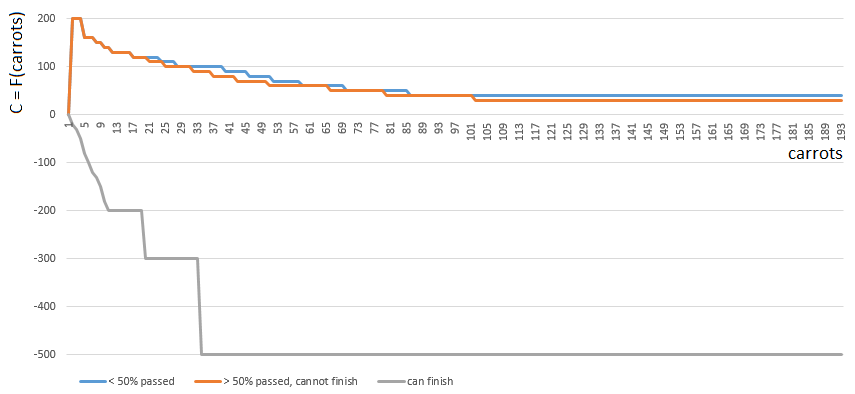
Las funciones 0 y 1 son similares: el "valor" de cada zanahoria en las manos del jugador disminuye gradualmente a medida que aumenta el número de zanahorias en las manos. El juego rara vez alienta a los Plyushkins. En el caso 1 (pasó la mitad del campo), el valor de las zanahorias disminuye un poco más rápido.
La función 2 (el jugador puede terminar), por el contrario, impone una gran multa (valor de coeficiente negativo) en cada zanahoria en las manos del jugador: cuantas más zanahorias, mayor será el coeficiente de penalización. Dado que con un exceso de zanahorias, el final está prohibido por las reglas del juego.
Antes de calcular la cantidad de zanahorias en las manos del jugador se especifica teniendo en cuenta las zanahorias por movimiento desde la celda de lechuga / celda número 1 ... 4.
Una "
lechuga " de grado S se deduce de manera similar. Dependiendo de la cantidad de ensalada en las manos del jugador (0 ... 3), se selecciona una función
S0,S1,S2 o
S3 . Argumento de la función
S0−S3 . - de nuevo, la ruta "relativa" recorrida por el jugador. A saber, el número de celdas con ensalada restante en el frente (en relación con la celda ocupada por el jugador):
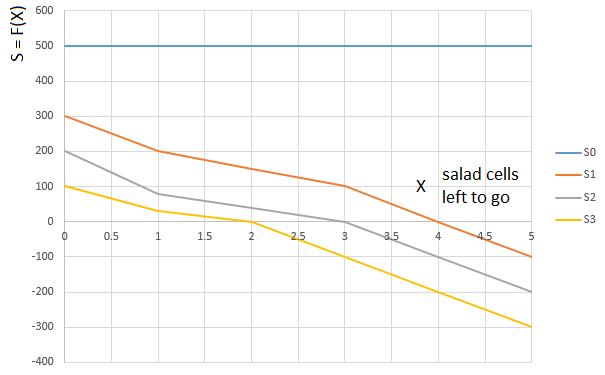
La curva
S0 - función de evaluación (S) del número de celdas de lechuga frente al jugador (0 ... 5), para un jugador con 0 cartas de lechuga en la mano,
la curva
S1 - la misma función para un jugador con una carta de ensalada en la mano, etc.
La calificación final (E = Ks * S + Kc * C + Kp * P) tiene en cuenta:
- la cantidad extra de zanahorias que recibirá el jugador inmediatamente antes de su propio movimiento,
- el camino del jugador
- la cantidad de zanahorias y lechugas en las manos que afectan de manera no lineal al puntaje.
Y así es como juega una computadora, eligiendo el siguiente movimiento con la puntuación heurística máxima:
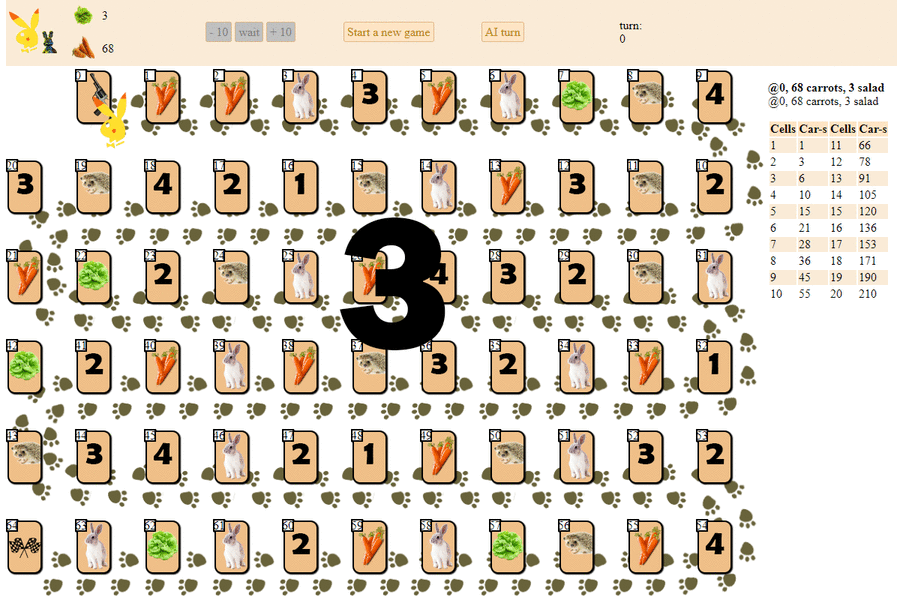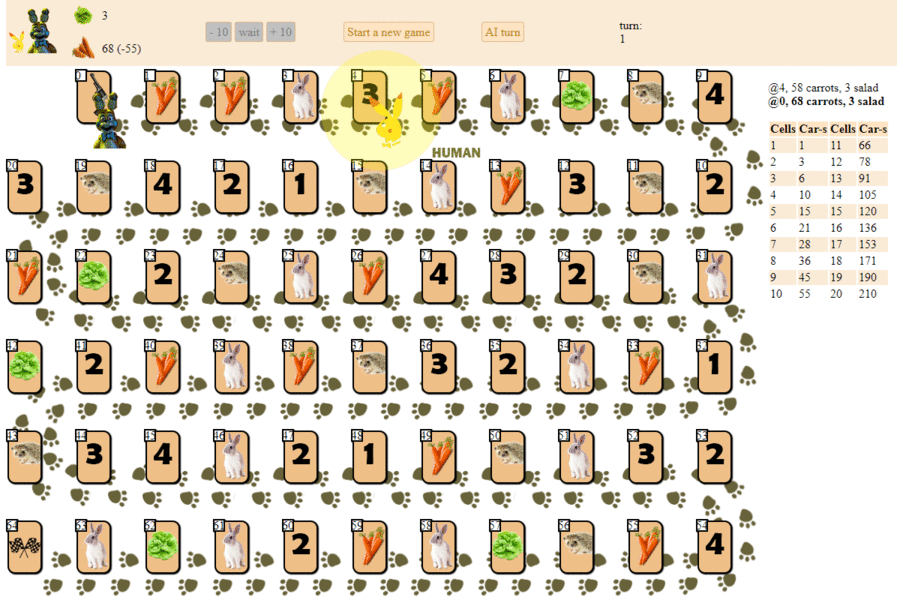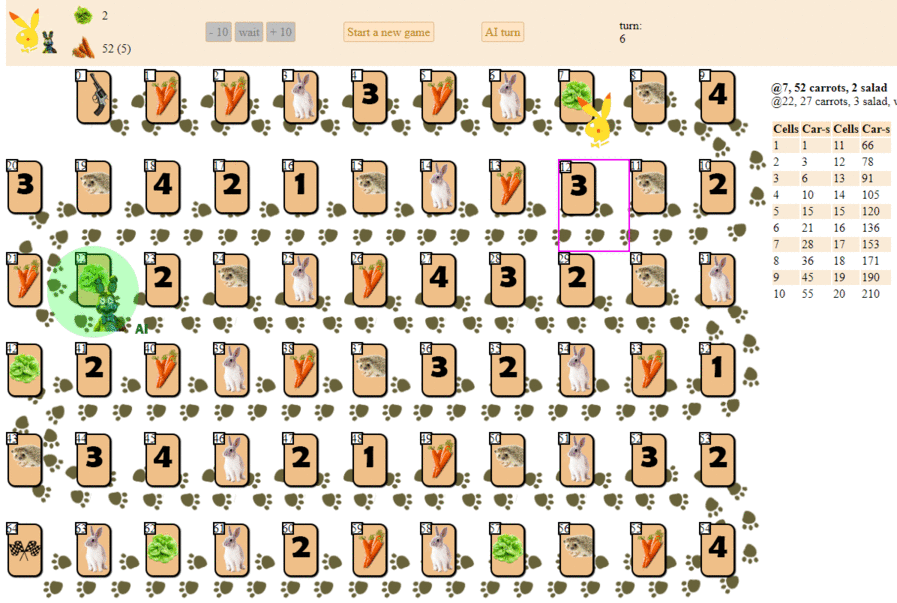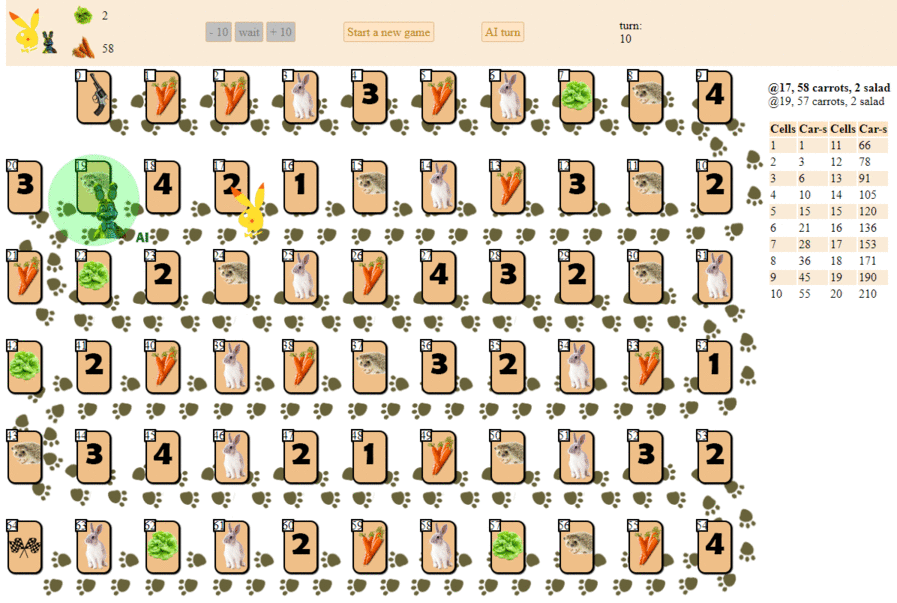
En principio, el debut no es tan malo. Sin embargo, uno no debería esperar un buen juego de esa IA: a la mitad del juego, el "robot" verde comienza a hacer movimientos repetidos, y al final realiza varias iteraciones de movimientos hacia adelante, hacia atrás hasta el erizo, hasta que finalmente termina. En parte debido al azar, terminará detrás del jugador, una persona por una docena de movimientos.
Notas de implementacionEl cálculo de la evaluación es administrado por una clase especial: Calculador de estimación. Las funciones para evaluar la posición con respecto a las tarjetas de ensalada de zanahoria se cargan en matrices en el constructor estático de la clase calculadora. En la entrada, el método de estimación de posición recibe el objeto de posición en sí y el índice del jugador, desde el "punto de vista" desde el cual el algoritmo evalúa la posición. Es decir, la misma posición de juego puede recibir varias clasificaciones diferentes, según el jugador para el que se consideran los puntos virtuales.
Árbol de decisión y algoritmo Minimax
Utilizamos el algoritmo de toma de decisiones en el juego antagonista de Minimax. Muy bien, en mi opinión, el algoritmo se describe en
esta publicación (traducción) .
Enseñamos al programa a "mirar" algunos movimientos adelante. Supongamos que, desde la posición actual (y el fondo no es importante para el algoritmo, como recordamos, el programa funciona como
una máquina Moore ), numerado por el número 1, el programa puede hacer dos movimientos. Tenemos dos posiciones posibles, 2 y 3. Luego viene el turno del jugador - la persona (en el caso general - el enemigo). Desde la segunda posición, el oponente tiene 3 movimientos, desde el tercero, solo dos movimientos. Luego, el turno para hacer un movimiento nuevamente cae en el programa, que, en total, puede hacer 10 movimientos desde 5 posibles posiciones:
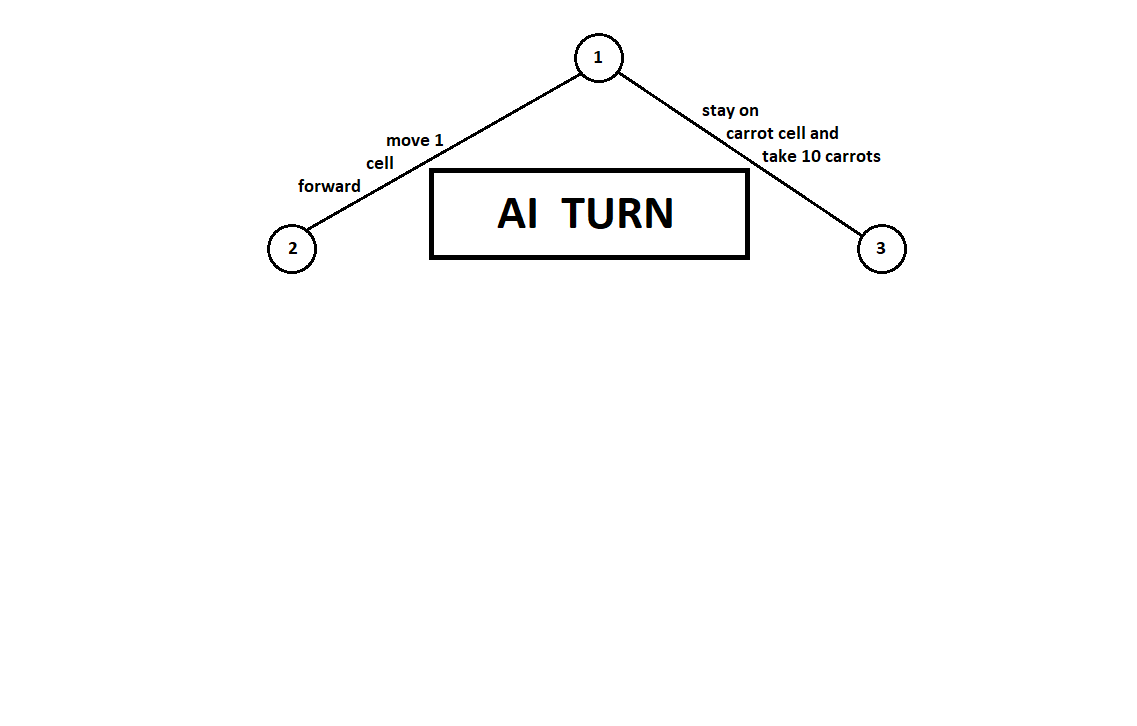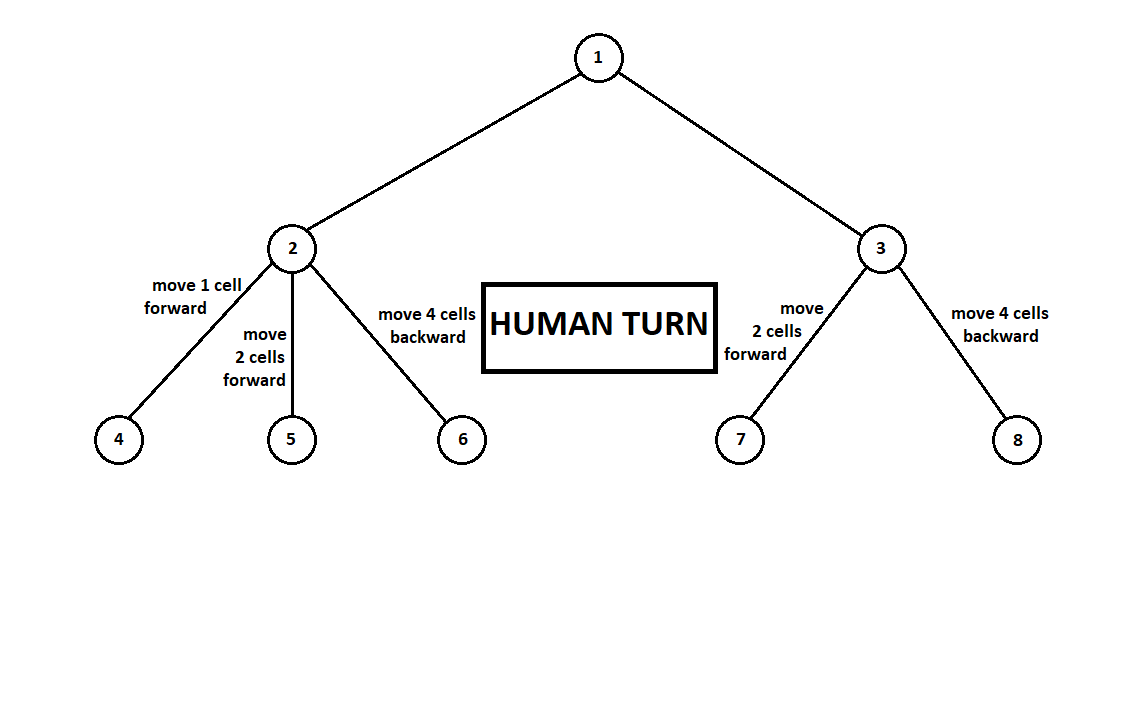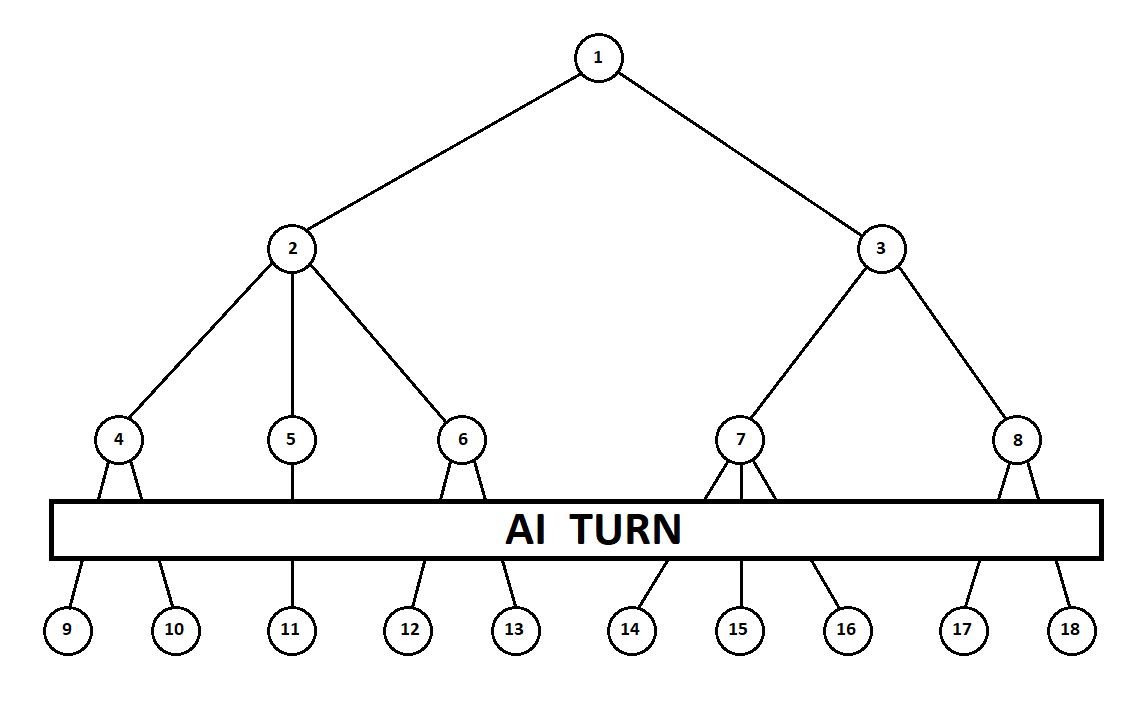
Supongamos que, después del segundo movimiento de la computadora, el juego termina y cada una de las posiciones recibidas se evalúa desde el punto de vista del primer y segundo jugador. Y ya hemos implementado el algoritmo de evaluación. Evaluemos cada una de las posiciones finales (hojas del árbol 9 ... 18) en forma de vector
[v0,v1] ,
donde
v0 - puntuación calculada para el primer jugador,
v1 - puntuación del segundo jugador:
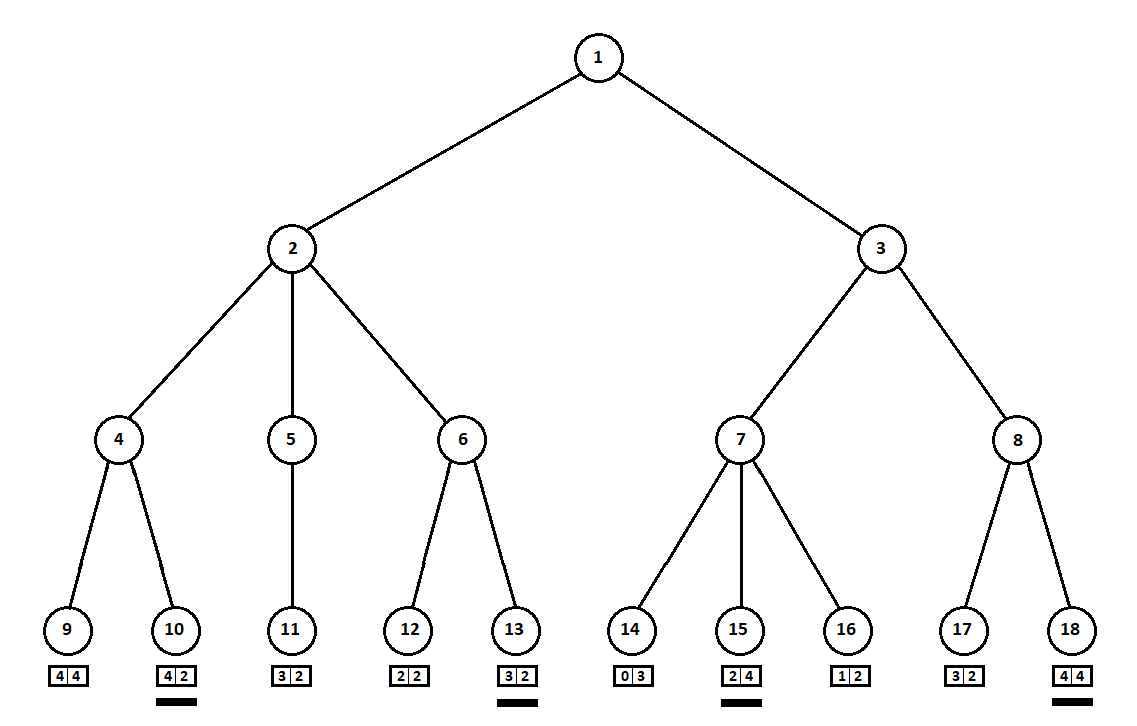
Como la computadora hace el último movimiento, obviamente elegirá las opciones en cada uno de los subárboles ([9, 10], [11], [12, 13], [14, 15, 16], [17, 18]) lo que le da una mejor calificación. La pregunta surge de inmediato: ¿por qué principio se debe elegir la "mejor" posición?
Por ejemplo, hay dos movimientos, después de los cuales tenemos posiciones con calificaciones [5; 5] y [2; 1] Evalúa al primer jugador. Dos alternativas son obvias:
- selección de posición con el valor absoluto máximo de la i-ésima puntuación para el i-ésimo jugador. En otras palabras, el noble corredor Leslie, ansioso por la victoria, sin tener en cuenta a los competidores. En este caso, una posición con una estimación de [5; 5]
- La elección de un puesto con la calificación máxima en relación con las estimaciones de los competidores es la astuta profesora Faith, que no pierde la oportunidad de infligir trucos sucios al enemigo. Por ejemplo, intencionalmente va a la zaga de un jugador que planea comenzar desde la segunda posición. Un artículo con calificación [2; 1]
En mi implementación de software, hice el algoritmo de selección de calificación (una función que asigna el vector de calificación a un valor escalar para el i-ésimo jugador) un parámetro personalizado. Pruebas posteriores mostraron, para mi sorpresa, la superioridad de la primera estrategia: la elección de la posición por el valor absoluto máximo
vi .
Características de la implementación de software.Si la primera opción para elegir la mejor calificación se especifica en la configuración de la IA (clase TurnMaker), el código del método correspondiente tomará la forma:
int ContractEstimateByAbsMax(int[] estimationVector, int playerIndex) { return estimationVector[playerIndex]; }
El segundo método, el máximo relativo a las posiciones de los competidores, se implementa un poco más complicado:
int ContractEstimateByRelativeNumber(int[]eVector, int player) { int? min = null; var pVal = eVector[player]; for (var i = 0; i < eVector.Length; i++) { if (i == player) continue; var val = pVal - eVector[i]; if (!min.HasValue || min.Value > val) min = val; } return min.Value; }
Las estimaciones seleccionadas (subrayadas en la figura) se transfieren al nivel superior. Ahora el enemigo tiene que elegir una posición, sabiendo qué posición posterior elegirá el algoritmo:
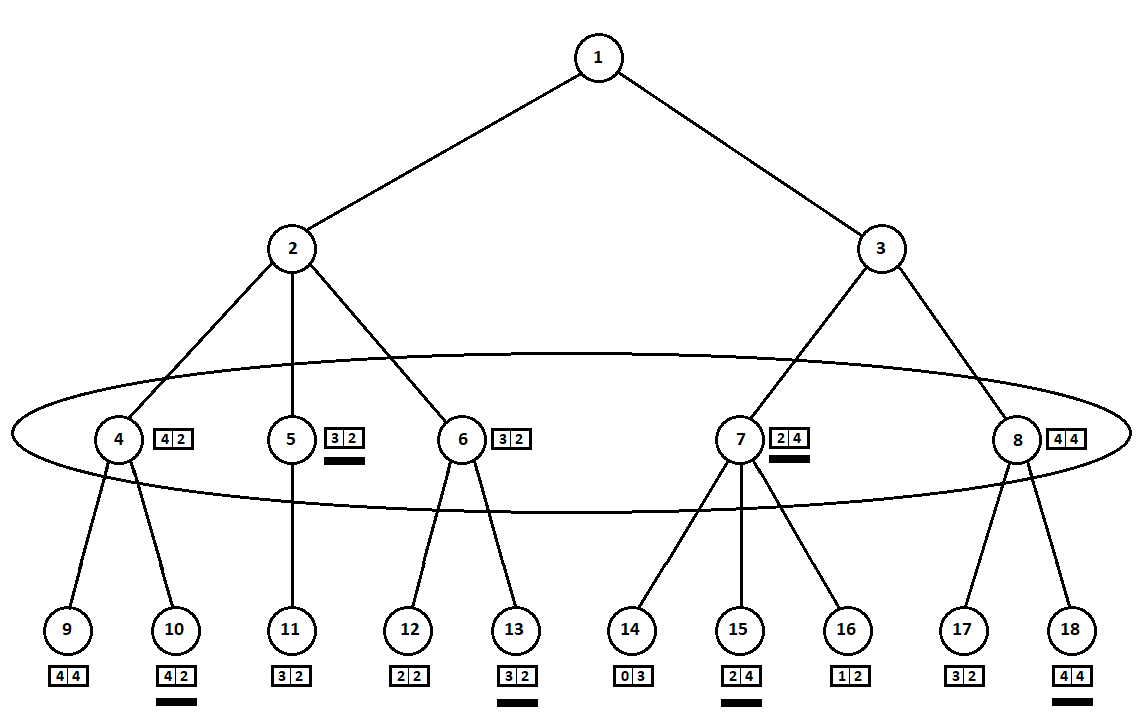
El adversario, obviamente, elegirá la posición con la mejor calificación para sí mismo (aquella en la que la
segunda coordenada del vector toma el mayor valor). Estas estimaciones se subrayan nuevamente en el gráfico.
Finalmente, volvemos al primer movimiento. La computadora selecciona, y él prefiere el movimiento con la primera coordenada más grande del vector:
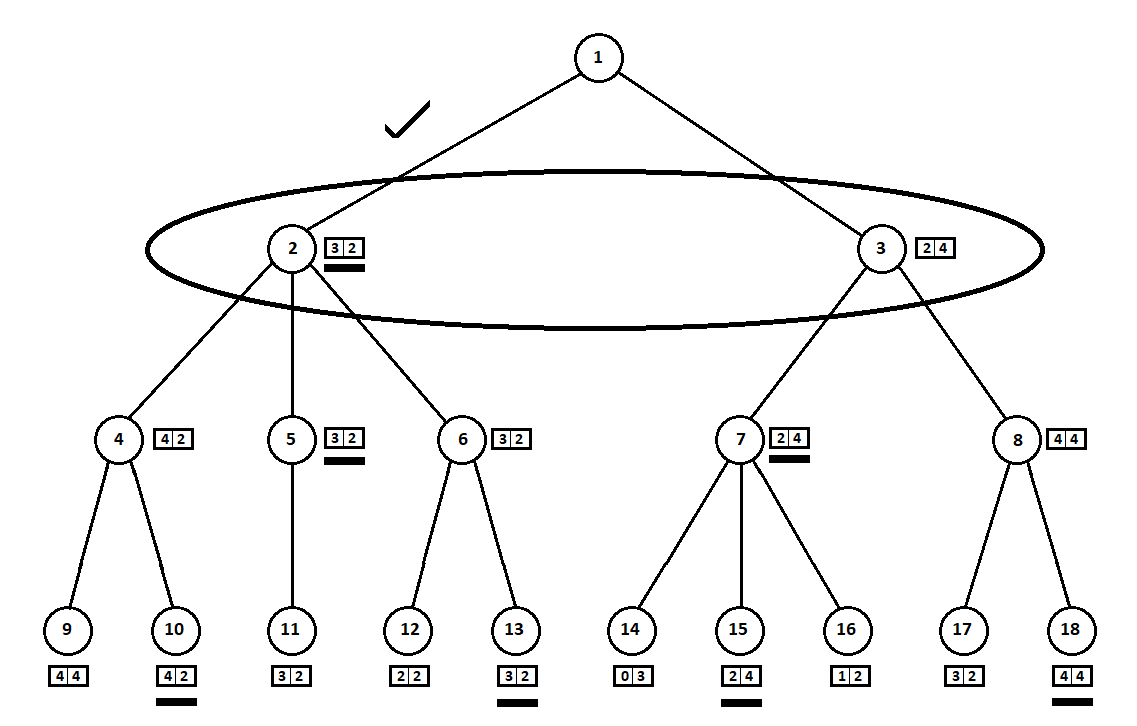
Por lo tanto, el problema está resuelto: se encuentra un movimiento casi óptimo. Supongamos que una puntuación heurística del 100% en las posiciones de las hojas en un árbol indica un futuro ganador. Entonces nuestro algoritmo elegirá inequívocamente el mejor movimiento posible.
Sin embargo, el puntaje heurístico es 100% exacto solo cuando se evalúa la posición
final del juego: uno (o varios) jugadores han terminado, se determina el ganador. Por lo tanto, al tener la oportunidad de mirar hacia adelante N movimientos: tanto como sea necesario para ganar rivales con la misma fuerza, puedes elegir el movimiento óptimo.
Pero un juego típico para 2 jugadores dura en promedio entre 30 y 40 movimientos (para tres jugadores, alrededor de 60 movimientos, etc.). Desde cada posición, un jugador generalmente puede hacer unos 8 movimientos. En consecuencia, un árbol completo de posibles posiciones para 30 movimientos consistirá en aproximadamente
830 = 1237940039285380274899124224 picos!
En la práctica, construir y "analizar" un árbol de ~ 100,000 posiciones en mi PC toma alrededor de 300 milisegundos. Lo que nos da un límite en la profundidad del árbol en 7 a 8 niveles (movimientos), si queremos esperar una respuesta de la computadora de no más de un segundo.
Características de la implementación de software.Obviamente, se requiere un método recursivo para construir un árbol de posiciones y encontrar el mejor movimiento. En la entrada del método: la posición actual (en la que, como recordamos, el jugador ya está haciendo un movimiento) y el nivel del árbol actual (número de movimiento). Tan pronto como descendemos al nivel máximo permitido por la configuración del algoritmo, la función devuelve un vector de estimación de posición heurística desde el "punto de vista" de cada uno de los jugadores.
Una adición importante : el descenso debajo del árbol también debe detenerse cuando el jugador actual haya terminado. De lo contrario (si se selecciona el algoritmo para seleccionar la mejor posición en relación con las posiciones de otros jugadores), el programa puede "pisotear" al final durante mucho tiempo, "burlarse" del oponente. Además, de esta manera reduciremos ligeramente el tamaño del árbol en el final del juego.
Si aún no estamos en el último nivel de recursión, seleccionamos los movimientos posibles, creamos una nueva posición para cada movimiento y lo pasamos a la llamada recursiva del método actual.
¿Por qué es Minimax?En la interpretación original de los jugadores son siempre dos. El programa calcula el puntaje exclusivamente desde la posición del primer jugador. En consecuencia, al elegir la "mejor" posición, el jugador con índice 0 busca una posición con una calificación máxima, el jugador con índice 1 busca un mínimo.
En nuestro caso, la calificación debe ser un vector para que cada uno de los N jugadores pueda evaluarla desde su "punto de vista", ya que la calificación se eleva en el árbol.
Tuning AI
Mi práctica de jugar contra la computadora ha demostrado que el algoritmo no es tan malo, pero aún así es inferior a los humanos. Decidí mejorar la IA de dos maneras:
- optimizar la construcción / recorrido del árbol de decisión,
- Mejorar la heurística.
Optimización del algoritmo Minimax
En el ejemplo anterior, podríamos negarnos a considerar la posición 8 y “guardar” 2 - 3 vértices del árbol:
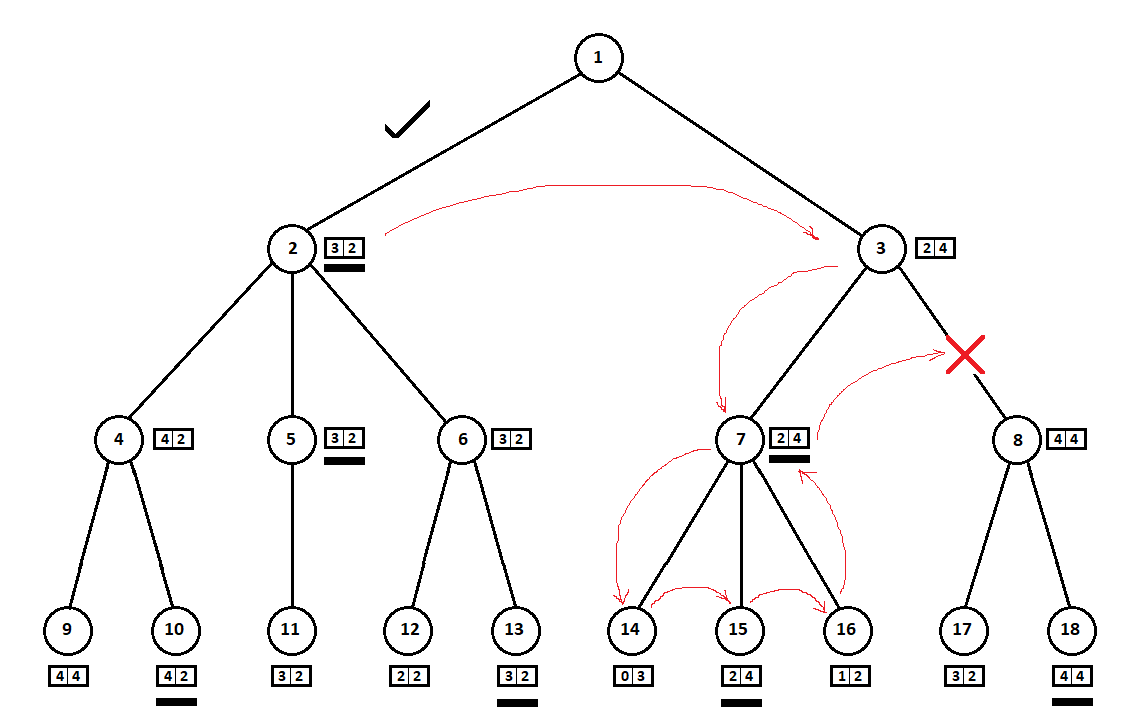
Caminamos alrededor del árbol de arriba a abajo, de izquierda a derecha. Sin pasar por el subárbol que comienza en la posición 2, dedujimos la mejor estimación para el movimiento 1 -> 2: [3, 2]. Sin pasar por el subárbol con la raíz en la posición 7, determinamos la calificación actual (mejor para el movimiento 3 -> 7): [2, 4]. Desde el punto de vista de la computadora (primer jugador), el puntaje [2, 4] es peor que el puntaje [3, 2]. Y dado que el oponente de la computadora elige el movimiento desde la posición 3, cualquiera que sea el puntaje para la posición 8, el puntaje final para la posición 3 será a priori peor que el puntaje obtenido para la tercera posición. En consecuencia, el subárbol con la raíz en la posición 8 no se puede construir ni evaluar.
La versión optimizada del algoritmo Minimax, que le permite cortar el exceso de subárboles, se llama
algoritmo de recorte alfa-beta . La implementación de este algoritmo requerirá modificaciones menores en el código fuente.
Características de la implementación de software.Además, se pasan dos parámetros enteros al método CalcEstimate de la clase TurnMaker: alpha, que es igual a int.MinValue inicialmente y beta, que es igual a int.MaxValue. Además, después de recibir una estimación del movimiento actual en consideración, se ejecuta un pseudocódigo del formulario:
e = _[0]
Una característica importante de la implementación de software.El método de recorte alfa-beta, por definición, conduce a la misma solución que el algoritmo Minimax "limpio". Para verificar si la lógica de la toma de decisiones ha cambiado (o más bien, los resultados son movimientos), escribí una prueba de unidad en la que el robot realizó 8 movimientos para cada uno de los 2 oponentes (16 movimientos en total) y guardó la serie de movimientos resultante, con opción de recorte deshabilitada .
Luego, en la misma prueba, el procedimiento se repitió con la opción de recorte activada . Después de eso, se comparó la secuencia de movimientos. La discrepancia en los movimientos indica un error en la implementación del algoritmo de recorte alfa-beta (prueba fallida).
Optimización de recorte alfa-beta menor
Con la opción de recorte habilitada en la configuración de AI, el número de vértices en el árbol de posición se redujo en un promedio de 3 veces. Este resultado puede ser algo mejorado.
En el ejemplo anterior:

"coincidió" con tanto éxito que, antes del subárbol con el vértice en la posición 3, examinamos el subárbol con el vértice en la posición 2. Si la secuencia era diferente, podríamos comenzar con el "peor" subárbol y no concluir que no tenía sentido considerar la siguiente posición .
Como regla general, el recorte en un árbol resulta ser más "económico", sus vértices descendientes en el mismo nivel (es decir, todos los movimientos posibles desde la posición i) ya están ordenados por la estimación de posición actual (sin mirar en profundidad). En otras palabras, suponemos que el mejor movimiento (desde el punto de vista heurístico) es más probable que obtenga una mejor calificación final. Por lo tanto, con cierta probabilidad, clasificamos el árbol para que el "mejor" subárbol sea considerado antes que el "peor", lo que nos permitirá cortar más opciones.
La evaluación de la posición actual es un procedimiento costoso. Si anteriormente era suficiente para nosotros evaluar solo las posiciones terminales (hojas), entonces ahora se realiza la evaluación para todos los vértices del árbol. Sin embargo, como lo mostraron las pruebas, el número total de estimaciones realizadas fue aún ligeramente menor que en la variante sin la clasificación inicial de posibles movimientos.
Características de la implementación de software.El algoritmo de recorte alfa-beta devuelve el mismo movimiento que el algoritmo original de Minimax. Esto verifica la prueba unitaria que escribimos, comparando dos secuencias de movimientos (para un algoritmo con recorte y sin él). El recorte alfa-beta con clasificación , en el caso general, puede indicar un movimiento diferente como cuasi óptimo.
Para probar el funcionamiento correcto del algoritmo modificado, necesita una nueva prueba. A pesar de la modificación, el algoritmo ordenado debería producir exactamente el mismo vector de estimación final ([3, 2] en el ejemplo de la figura) que el algoritmo no ordenado como el algoritmo original de Minimax.
En la prueba, creé una serie de posiciones de prueba y las seleccioné de acuerdo con el "mejor" movimiento, activando y desactivando la opción de clasificación. Luego comparó el vector de evaluación obtenido de dos maneras.
Además, dado que las posiciones para cada uno de los posibles movimientos en el vértice actual del árbol se ordenan por evaluación heurística, la idea sugiere descartar inmediatamente algunas de las peores opciones. Por ejemplo, un jugador de ajedrez puede considerar un movimiento en el que sustituye su torre por un golpe de peón. Sin embargo, al "desenrollar" la situación en profundidad por 3, 4 ... movimientos hacia adelante, notará inmediatamente las opciones cuando, por ejemplo, el oponente ponga bajo ataque al obispo de su reina.
En la configuración de AI, configuro el vector de "recorte de las peores opciones". Por ejemplo, un vector de la forma [0, 0, 8, 8, 4] significa que:
- mirando un [0] y dos [0] pasos hacia adelante, el programa considerará todos los movimientos posibles, porque 0 ,
- [8] [8] , 8 “” , , ,
- mirando cinco o más pasos hacia adelante [4], el programa evaluará no más de 4 "mejores" movimientos.
Con la clasificación activada para el algoritmo de recorte alfa-beta y un vector similar en la configuración de recorte, el programa comenzó a gastar alrededor de 300 milisegundos para seleccionar un movimiento cuasi óptimo, "profundizando" 8 pasos hacia adelante.Optimización Heurística
A pesar de la cantidad decente de posiciones de vértice iteradas en el árbol y "profundas" mirando hacia adelante en busca de un movimiento cuasi óptimo, la IA tenía varias debilidades. Definí uno de ellos como una " trampa de conejo ".Trampa de liebre. ( 8 — 10 15), . “” ( !):
. :
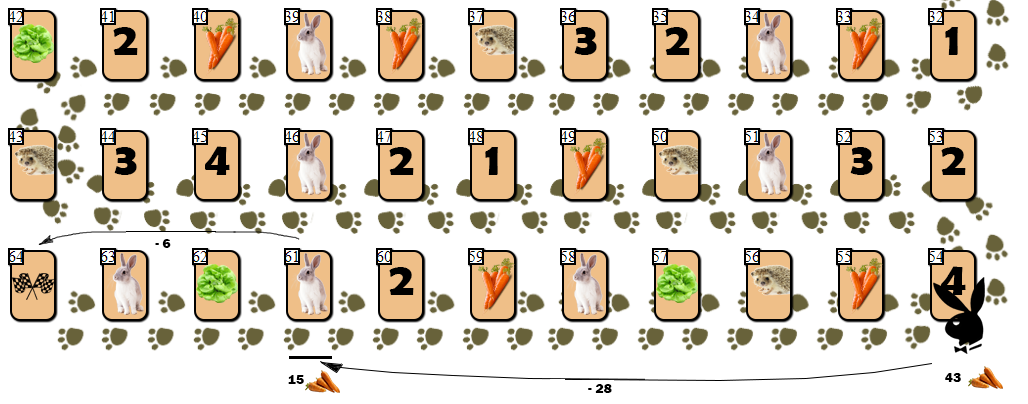
54 (43), — 10 55 . AI, , (61), 28 . , 6 9 ( 10 ).
, ( ), , 4 — 6 . , , , AI ?
,
, . AI . , , . “ ” :
65 — “” , , . , , , () .
Factores de corrección
Anteriormente, citando la fórmula heurística para evaluar la posición actualE = Ks * S + Kc * C + Kp * P,mencioné, pero no describí, los factores de corrección.El hecho es que tanto la fórmula en sí como los conjuntos de funcionesC 0 . . C 2 , S 0 . . S 5 , fueron deducidos por mí intuitivamente, sobre la base de la llamada "Sentido común". Como mínimo, me gustaría seleccionar tales coeficientes Ks, Kc y Kp para que la estimación sea lo más adecuada posible. ¿Cómo evaluar la "adecuación" de la evaluación? La evaluación es una cantidad adimensional y solo se puede comparar con otra estimación. Pude encontrar la única forma de refinar los coeficientes de corrección:puse en el programa una serie de "estudios" almacenados en un archivo CSV con datos del formulario 45;26;2;f;29;19;0;f;2 ...
Esta línea literalmente significa lo siguiente:- el primer jugador está en la casilla 45, tiene 26 cartas de zanahorias y 2 cartas de ensalada en sus manos, el jugador no pierde un movimiento (f = falso). El derecho a moverse es siempre el primer jugador.
- el segundo jugador en la celda 29 con 19 cartas de zanahorias y sin cartas de ensalada, no se pierde un movimiento.
- la figura dos significa que, "decidiendo" el estudio, asumí que el segundo jugador está en una situación ganadora.
Después de poner 20 bocetos en el programa, los "descargué" en el cliente web del juego, y luego ordené cada boceto. Analizando el boceto, alternativamente hice movimientos para cada uno de los jugadores, hasta que me decidí por el "ganador". Una vez finalizada la evaluación, la envié en un equipo especial al servidor.Después de evaluar 20 estudios (por supuesto, valdría la pena analizar más de ellos), evalué cada uno de ellos por el programa. En la evaluación, los valores de cada uno de los factores de corrección, de 0.5 a 2 en incrementos de 0.1 - total16 3 = 4096 variantes de triples de coeficientes. Si el puntaje para el primer jugador resultó ser más alto que el puntaje del segundo jugador, y se almacenó una instrucción similar en la línea del registro de estudio (el último valor de la línea es 1), se contó el "hit". Del mismo modo para una situación espejo. De lo contrario, se contaba un deslizamiento. Como resultado, elegí los triples para los cuales el porcentaje de "golpes" era máximo (16 de 20). Salieron alrededor de 250 de 4096 vectores, de los cuales seleccioné el "mejor", de nuevo, "a simple vista", y lo instalé en la configuración de AI.Resumen
Como resultado, obtuve un programa de trabajo que, como regla, me supera en la versión uno contra uno contra la computadora. Aún no se han acumulado estadísticas serias de victorias y derrotas para la versión actual del programa. Quizás la posterior sintonización fácil de IA hará que mis victorias sean imposibles. O casi imposible, ya que el factor de células de liebre aún permanece.Por ejemplo, en la lógica de elegir clasificaciones (máximo absoluto o máximo relativo a otros jugadores), definitivamente probaría una opción intermedia. Como mínimo, si el valor absoluto del puntaje del i-ésimo jugador es igual, es razonable elegir un movimiento que conduzca a una posición con un valor relativo más alto del puntaje (un híbrido del noble Leslie y el traicionero Feith).El programa es completamente funcional para la versión con 3 jugadores. Sin embargo, hay sospechas de que la "calidad" de los movimientos de IA para jugar con 3 jugadores es menor que para jugar con dos jugadores. Sin embargo, durante la última prueba perdí con la computadora, quizás por negligencia, evaluando casualmente la cantidad de zanahorias en mis manos y llegando a la meta con un exceso de "combustible".Hasta ahora, el desarrollo posterior de la IA se ve obstaculizado por la falta de una persona, un "probador", es decir, un oponente vivo de un "genio" de la computadora. Yo mismo jugué lo suficiente de Hare y Hedgehog para causar náuseas y me vi obligado a interrumpir en la etapa actual.→ Enlace al repositorio con fuente