Necesita más desenfoques diferentes

El desenfoque de imagen con el filtro Gaussian Blur se usa ampliamente en una amplia variedad de tareas. Pero a veces desea un poco más de variedad que un solo filtro para todas las ocasiones, en el que solo un parámetro se presta para el ajuste: su tamaño. En este artículo, veremos varias otras implementaciones de desenfoque.

Introduccion

El efecto Desenfoque gaussiano es una operación lineal y matemáticamente representa una convolución de la imagen con la matriz de filtro. En este caso, cada píxel de la imagen se reemplaza por la suma de los cercanos tomados con ciertos factores de ponderación.

El filtro se llama gaussiano porque está construido a partir de una función conocida como gaussiano, $$$e ^ {- x ^ 2}$ :



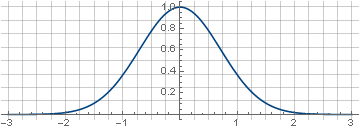
una versión bidimensional de la cual se obtiene por su rotación alrededor del eje de ordenadas, $$$e ^ {- (x ^ 2 + y ^ 2)}$ :



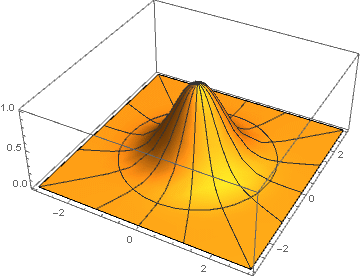
Aquí para cada par de coordenadas $$$(x, y)$ la distancia al centro se calcula mediante la fórmula $$$\ sqrt {x ^ 2 + y ^ 2}$ , que se pasa como argumento a la función gaussiana y, como puede ver fácilmente, $$$e ^ {- \ left (\ sqrt {x ^ 2 + y ^ 2} \ right) ^ 2}$ reducido a $$$e ^ {- (x ^ 2 + y ^ 2)}$ .

Matriz construida en un segmento $$$[- 3.3]$ y con cierto nivel de muestreo, se verá así:

$$

$$\ left (\ begin {array} {ccccccc} 1.52 \ times 10 ^ {- 8} & 2.26 \ times 10 ^ {- 6} y 0.0000454 y 0.000123 y 0.0000454 y 2.26 \ times 10 ^ {- 6} y 1.52 \ veces 10 ^ {- 8} \\ 2.26 \ veces 10 ^ {- 6} y 0.000335 y 0.00674 y 0.0183 y 0.00674 y 0.000335 y 2.26 \ veces 10 ^ {- 6} \\ 0.0000454 y 0.00674 y 0.135 y 0.368 y 0.135 & 0.00674 & 0.0000454 \\ 0.000123 & 0.0183 & 0.368 & 1.00 & 0.368 & 0.0183 & 0.000123 \\ 0.0000454 & 0.00674 & 0.135 & 0.368 & 0.135 & 0.00674 & 0.0000454 \\ 2.26 \ times 10 ^ {- 6} & 0.000335 & 0.00674 & 0.0183 y 0.00674 y 0.000335 y 2.26 \ veces 10 ^ {- 6} \\ 1.52 \ veces 10 ^ {- 8} y 2.26 \ veces 10 ^ {- 6} y 0.0000454 y 0.000123 y 0.0000454 y 2.26 \ veces 10 ^ { -6} y 1.52 \ veces 10 ^ {- 8} \\ \ end {array} \ right)$$

O, si consideramos los valores de los elementos de la matriz como un nivel de brillo, así:



En términos de procesamiento de señal, esto se llama respuesta de impulso, ya que esto es exactamente lo que se verá el resultado de la convolución de este filtro con un solo impulso (en este caso, un píxel).

Inicialmente, un gaussiano se define en un intervalo infinito. Pero debido al hecho de que decae bastante rápido, es posible excluir de los cálculos valores cercanos a cero, ya que aún no afectarán el resultado. En aplicaciones reales, la normalización del valor también es necesaria para que después de la convolución el brillo de la imagen no cambie; y en el caso de desenfocar una imagen en la que cada píxel tiene el mismo color, la imagen en sí no debería cambiar.

Por conveniencia, la normalización también se usa a menudo en coordenadas, al introducir un parámetro adicional $$$\ sigma$ (leer como "sigma") - para considerar un argumento en el rango $$$[- 1,1]$ y $$$\ sigma$ determina la relación de compresión del gaussiano:

$$

$$\ frac {e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

Divisor Normalizador $$$2 \ pi \ sigma ^ 2$ obtenido aquí analíticamente a través de una integral definida en el infinito:

$$

$$\ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \, dx dy = 2 \ pi \ sigma ^ 2$$

Debido al hecho de que la igualdad es válida $$$e ^ {- \ left (x ^ 2 + y ^ 2 \ right)} = e ^ {- x ^ 2} e ^ {- y ^ 2}$ El desenfoque gaussiano se puede implementar secuencialmente, primero en filas y luego en columnas, lo que le permite ahorrar bastante en los cálculos. En este caso, es necesario utilizar la fórmula de normalización para el caso unidimensional:

$$

$$\ frac {e ^ {- \ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

Inicio

Para un filtro arbitrario, primero debemos definir nuestra propia función de atenuación a partir de una variable $$$f$ , a partir del cual la función de dos variables se obtiene por rotación reemplazando $$$x$ en $$$\ sqrt {x ^ 2 + y ^ 2}$ donde $$$x$ y $$$y$ Estas son las coordenadas del elemento matriz en el rango $$$(- 1,1)$ , y que se utiliza para completar los elementos de la matriz. La normalización no se considerará analíticamente, sino una suma directa de todos los elementos de la matriz, esto es más simple y más preciso, ya que después de la discretización, la función se "diluye" y el valor de normalización dependerá del nivel de discretización.

En caso de que los elementos de la matriz estén numerados desde cero, la coordenada $$$x$ o $$$y$ se calcula mediante la fórmula

$$

$$\ frac {2 index} {size-1} -1$$

donde $$$index$ - el número de serie del elemento en la fila o columna, y $$$talla$ - número total de elementos.

Por ejemplo, para una matriz de 5 por 5, se vería así:

$$

$$\ left (\ begin {array} {ccccc} f (-1, -1) & f \ left (- \ frac {1} {2}, - 1 \ right) & f (0, -1) & f \ left (\ frac {1} {2}, - 1 \ right) & f (1, -1) \\ f \ left (-1, - \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, - \ frac {1} {2} \ right) & f \ left (0, - \ frac {1} {2} \ right) & f \ left (\ frac { 1} {2}, - \ frac {1} {2} \ right) & f \ left (1, - \ frac {1} {2} \ right) \\ f (-1.0) & f \ left (- \ frac {1} {2}, 0 \ right) & f (0,0) & f \ left (\ frac {1} {2}, 0 \ right) & f (1,0) \\ f \ left (-1, \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (0, \ frac {1} {2} \ right) & f \ left (\ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (1, \ frac {1} {2 } \ right) \\ f (-1,1) & f \ left (- \ frac {1} {2}, 1 \ right) & f (0,1) & f \ left (\ frac {1} { 2}, 1 \ right) & f (1,1) \\ \ end {array} \ right)$$

O, si excluimos los valores límite que aún son cero, entonces las coordenadas serán calculadas por la fórmula

$$

$$\ frac {2 index-size + 1} {size}$$

y la matriz tomará la forma correspondiente

$$

$$\ left (\ begin {array} {ccccc} f \ left (- \ frac {4} {5}, - \ frac {4} {5} \ right) & f \ left (- \ frac {2} { 5}, - \ frac {4} {5} \ right) & f \ left (0, - \ frac {4} {5} \ right) & f \ left (\ frac {2} {5}, - \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, - \ frac {4} {5} \ right) \\ f \ left (- \ frac {4} {5 }, - \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (0, - \ frac {2} {5} \ right) & f \ left (\ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (\ frac {4} {5}, - \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5}, 0 \ right) & f \ left (- \ frac {2} {5}, 0 \ right ) & f (0,0) & f \ left (\ frac {2} {5}, 0 \ right) & f \ left (\ frac {4} {5}, 0 \ right) \\ f \ left ( - \ frac {4} {5}, \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}, \ frac {2} {5} \ right) & f \ left (0, \ frac {2} {5} \ right) & f \ left (\ frac {2} {5}, \ frac {2} {5} \ right) & f \ left (\ frac {4} {5}, \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5}, \ frac {4} {5} \ right) & f \ left (- \ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (0, \ frac {4} {5} \ right) & f \ left (\ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, \ frac {4} {5} \ right) \\ \ end {array} \ right)$$

Después de que los elementos de la matriz hayan sido calculados por la fórmula, es necesario calcular su suma y dividir la matriz en ella. Por ejemplo, si obtenemos una matriz

$$

$$\ left (\ begin {array} {ccc} 1 y 4 y 1 \\ 4 y 20 y 4 \\ 1 y 4 y 1 \\ \ end {array} \ right)$$

entonces la suma de todos sus elementos será 40, y después de la normalización tomará la forma

$$

$$\ left (\ begin {array} {ccc} \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ frac {1} {10} & \ frac {1} {2} & \ frac {1} {10} \\ \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ end {array } \ right)$$

y la suma de todos sus elementos se convierte en 1.

Atenuación lineal

Primero, tome la función más simple: la línea:

$$

$$\ left \ {\ begin {array} {ll} 1-x, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

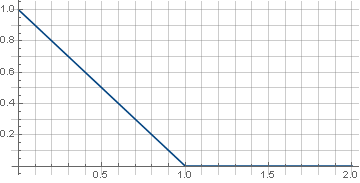
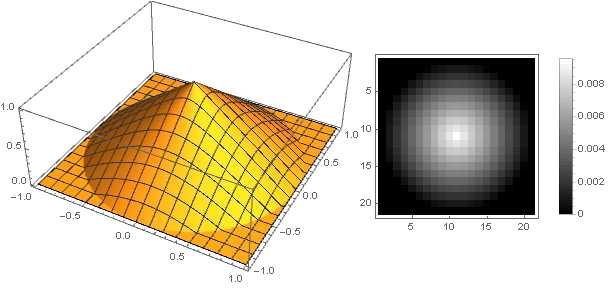
Una definición continua por partes requiere que se garantice que la función vaya a cero y que no aparezcan artefactos en las esquinas de la matriz durante la rotación. Además, dado que la rotación usa la raíz de la suma de los cuadrados de las coordenadas, que siempre es positiva, es suficiente para determinar la función solo en la parte positiva de los valores. Como resultado, obtenemos:

Atenuación lineal suave

Una transición brusca de una línea oblicua a cero funciones puede causar una contradicción con un sentido de belleza. Para resolverlo, la función nos ayudará.

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

en el cual $$$n$ determina la "rigidez" del acoplamiento, $$$n> 1$ . Por ejemplo $$$n = 3$ tenemos

$$

$$\ left \ {\ begin {array} {ll} 1- \ frac {3 xx ^ 3} {2}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right. $$$

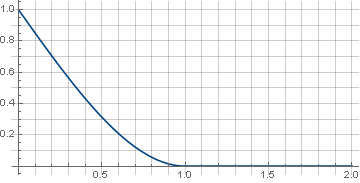
y el filtro en sí se verá como

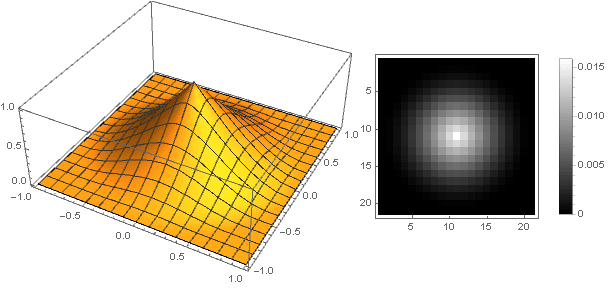
Atenuación hiperbólica

El filtro se puede hacer más "nítido" e ir más fácilmente a cero tomando otra función, por ejemplo, una hipérbola, y asegurando una transición suave a cero sumando con una parábola.



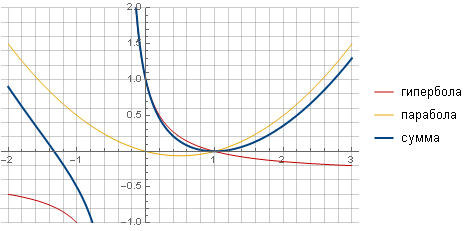
Después de todos los cálculos y simplificaciones, obtenemos la fórmula

$$

$$\ left \ {\ begin {array} {ll} \ frac {(x-1) ^ 2 (k x + k + 1)} {(k + 1) (k x + 1)}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

en que parámetro $$$k> 0$ determina la naturaleza de la atenuación:



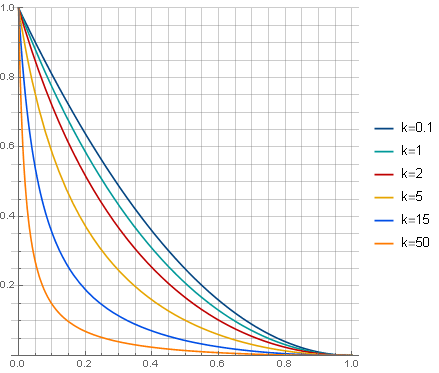
y el filtro en sí se verá (para $$$k = 5$ ) cómo

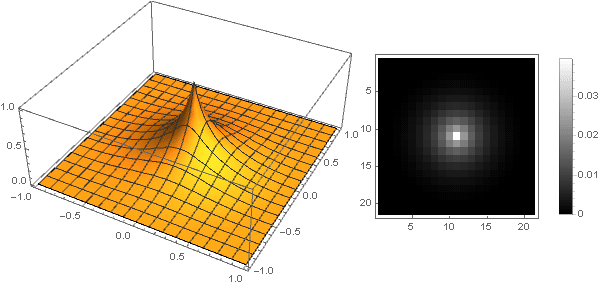
Efecto Bokeh

Puede ir por otro lado: hacer que la parte superior del filtro no sea afilada, sino estúpida. La forma más fácil de implementar esto es establecer la función de amortiguación como una constante:

$$

$$\ left \ {\ begin {array} {ll} 1, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

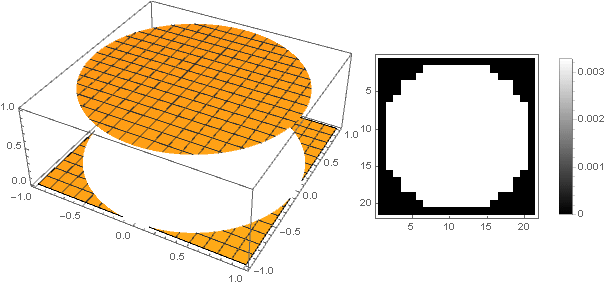
Pero en este caso, obtenemos una fuerte pixelación, que contrasta con la sensación de belleza. Para que sea más suave en los bordes, una parábola de orden superior nos ayudará, desde la cual, moviéndola a lo largo del eje de ordenadas y cuadrándola, obtenemos

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right. $$$

Parámetros variables $$$n$ Puede obtener una amplia gama de opciones de filtro:

$$

$$n = 0.5$$

$$

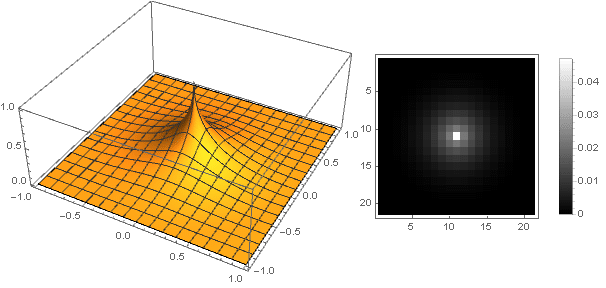
$$n = 2$$

$$

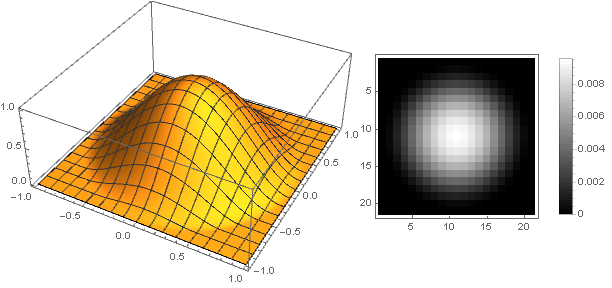
$$n = 10$$

$$

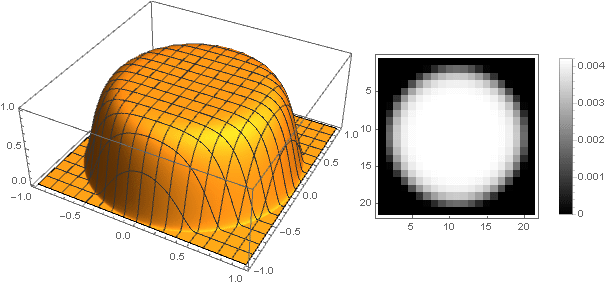
$$n = 50$$

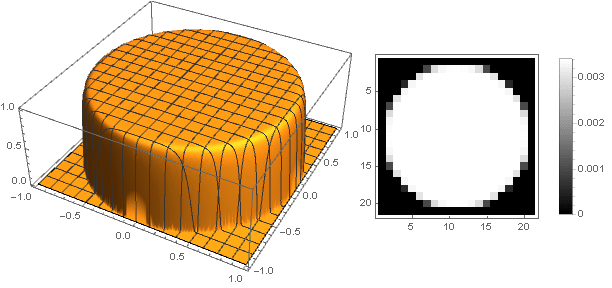
Y modificando ligeramente la función de amortiguación, puede hacer que el anillo en los bordes del filtro sea más pronunciado, por ejemplo así:

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2 \ left (d + x ^ m \ right), & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

Aquí parámetro $$$d$ determina la altura del centro y $$$m$ - la nitidez de la transición a los bordes.
Para $$$d = 0.2, m = 2, n = 10$ tenemos



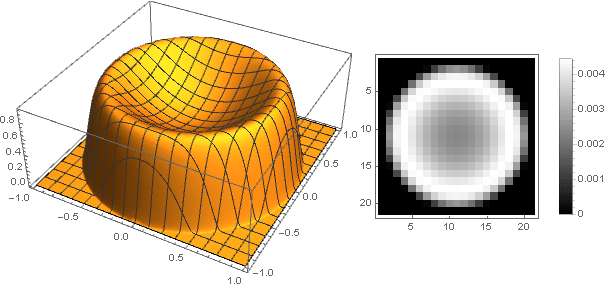
pero para $$$d = 0, m = 12, n = 2$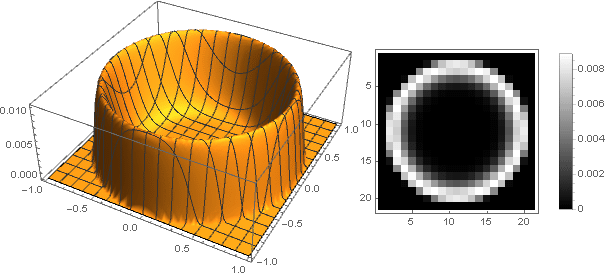

Variaciones gaussianas

La función del propio gaussiano también se puede modificar directamente. La forma más obvia de hacer esto es parametrizar el exponente; no lo consideraremos ahora, pero tomemos una opción más interesante:

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}, & -1 <x <1 \\ 0, y de lo contrario \\ \ end { matriz} \ right.$$

Debido al hecho de que con $$$x$ denominador de unidad $$$x ^ 2-1$ tiende a cero fracción $$$\ frac {k x ^ 2} {x ^ 2-1}$ tiende a menos infinito, y el exponente en sí también tiende a cero. Dividiendo así entre $$$x ^ 2-1$ permite comprimir el dominio de definición de función con $$$(- \ infty, \ infty)$ antes $$$(- 1,1)$ . Además, cuando $$$x = \ pm 1$ debido a la división por cero ( $$$1 ^ 2-1 = 0$ ) el valor de la función no está definido, pero tiene dos límites: el límite, por un lado (desde el interior), es cero y, por otro lado, infinito:

$$

$$\ underset {x \ a 1 ^ -} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ a 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

Dado que los valores límite no están incluidos en el intervalo, entonces cero en el límite en un lado es suficiente. Curiosamente, esta propiedad se extiende a todos los derivados de esta función, lo que garantiza una coincidencia perfecta con cero.

Parámetro $$$k$ determina la similitud con el gaussiano: cuanto más grande es, más fuerte se obtiene la similitud, debido al hecho de que una sección cada vez más lineal $$$\ frac {1} {x ^ 2-1}$ caer en el centro de la función. Uno podría suponer que debido a esto, en el límite, puede obtener el gaussiano original, pero, desafortunadamente, no, las funciones siguen siendo diferentes.



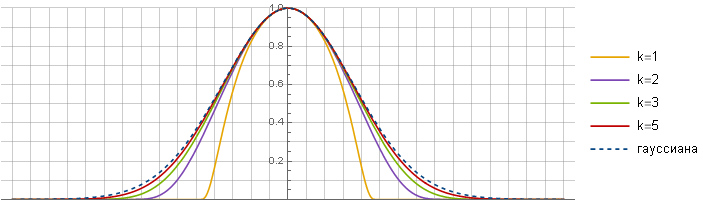
Ahora puedes ver lo que pasó:

$$

$$k = 5$$

$$

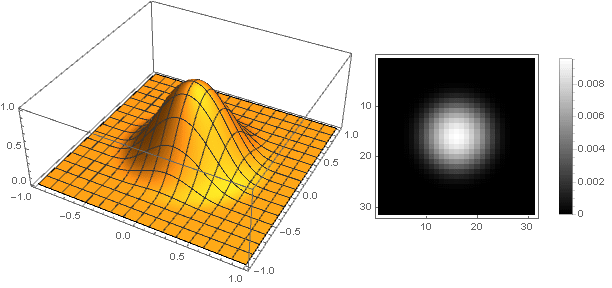
$$k = 2$$

$$

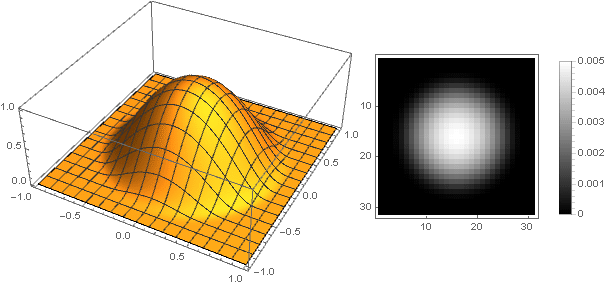
$$k = 0.5$$

$$

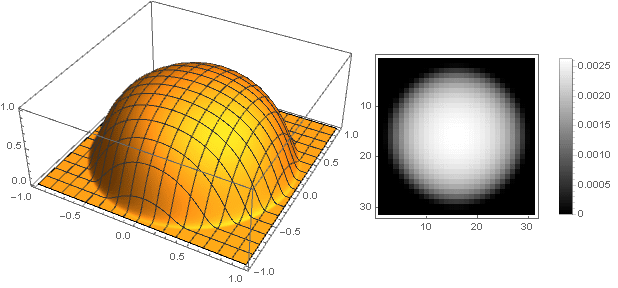
$$k = 0.1$$

$$

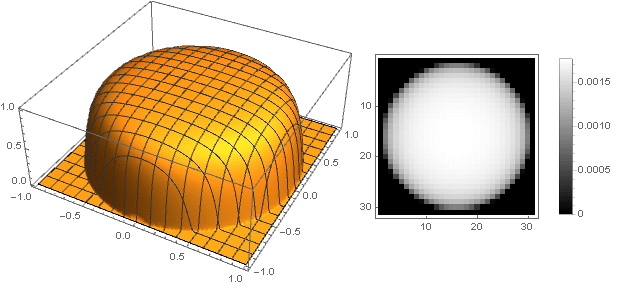
$$k = 0.01$$

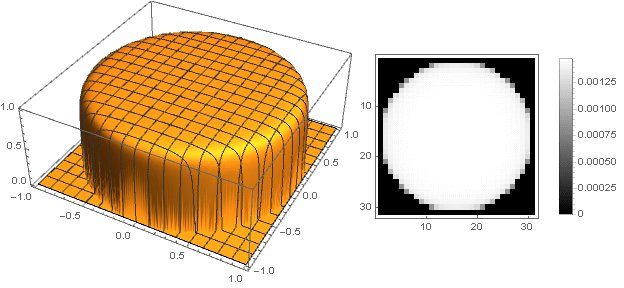
Variaciones de forma

Al cambiar la función de transición de dos coordenadas a una $$$\ sqrt {x ^ 2 + y ^ 2}$ , puede obtener otras formas, no solo un disco. Por ejemplo:

$$

$$f \ left (\ frac {\ left | x-y \ right | + \ left | x + y \ right |} {2} \ right)$$

$$

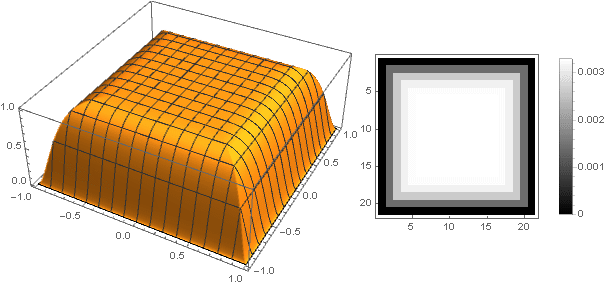
$$f (\ left | x \ right | + \ left | y \ right |)$$

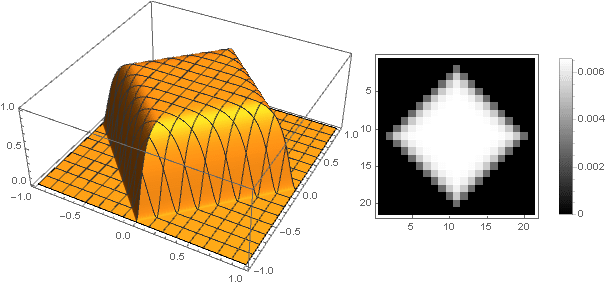
Al pasar a números complejos, puede construir figuras más complejas:

$$

$$f \ left (\ frac {\ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {0} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac { 2} {3}} \ right) \ right |} {\ sqrt {3}} \ right)$$

$$

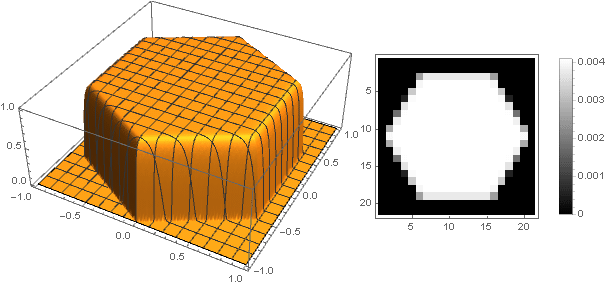
$$f \ biggl (10 \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {8}} \ right) \ right | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

$$

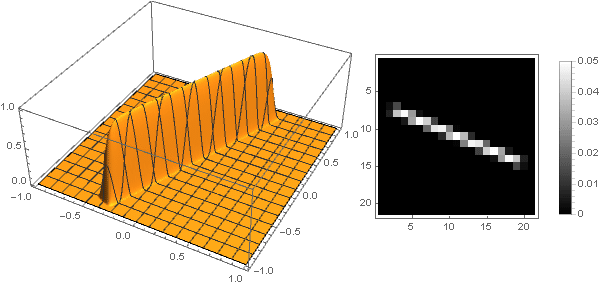
$$f \ biggl (\ biggl | 5 \ left | x + iy \ right | (x + iy) \ Re \ biggl (\ cos \ left (\ frac {5} {2} \ arg (x + iy) \ right ) \ biggr) \ biggr | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

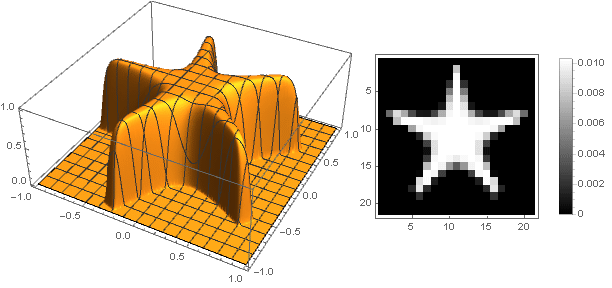
En este caso, debe asegurarse de que al convertir coordenadas no vaya más allá del intervalo $$$(0,1)$ - bueno, o viceversa, redefina la función de amortiguamiento para valores negativos del argumento.

Algunos ejemplos específicos

Un artículo no estaría completo sin una prueba práctica de imágenes específicas. Como no tenemos trabajo científico, tampoco tomaremos la imagen de Lena , tomaremos algo suave y esponjoso:


















Los mismos filtros, pero para texto:

Conclusión

Del mismo modo, puede crear filtros más complejos, incluidos aquellos con nitidez o contornos; y también modificar aquellos ya considerados.

De particular interés es el filtrado no lineal, cuando los valores de los coeficientes del filtro dependen de las coordenadas o de la imagen que se filtra directamente, pero esto ya es un tema para otros estudios.

La salida de funciones para acoplar con una constante se considera con más detalle aquí . Las funciones de ventana consideradas aquí también se pueden usar como la función de atenuación; todo lo que se necesita es escalar el argumento c (0,1) a ( $$$\ frac {1} {2}$ , 1) o inicialmente considere las funciones de la ventana mediante la fórmula $$$\ frac {1} {2} \ left (f \ left (\ frac {t x + 1} {t-1} \ right) -f \ left (\ frac {t x-1} {t-1} \ right) \ right)$ .

El documento fuente de Wolfram Mathematica para este artículo se puede descargar aquí .