Teoría de la felicidad. El vertiginoso vuelo de un sándwich con mantequilla

Sigo familiarizando a los lectores de Habr con los capítulos de su libro "Teoría de la felicidad" con el subtítulo "Fundamentos matemáticos de las leyes de la maldad". Este libro de ciencia popular aún no se ha publicado, informa de manera muy informal acerca de cómo las matemáticas le permiten mirar el mundo y la vida de las personas con un nuevo grado de conciencia. Es para aquellos que están interesados ​​en la ciencia y para aquellos que están interesados ​​en la vida. Y dado que nuestra vida es compleja y, en general, impredecible, el énfasis en el libro se centra principalmente en la teoría de la probabilidad y las estadísticas matemáticas. Aquí no se prueban los teoremas y no se dan los fundamentos de la ciencia, de ninguna manera es un libro de texto, sino lo que se llama ciencia recreativa. Pero es precisamente un enfoque tan lúdico que nos permite desarrollar la intuición, alegrar las conferencias para los estudiantes con ejemplos vívidos y, finalmente, explicar a los no matemáticos y a nuestros hijos que encontramos cosas tan interesantes en nuestra ciencia seca.



En este capítulo, examinamos la ley de un sándwich y organizamos un estudio completo utilizando el método de Monte Carlo y el análisis dimensional. Y finalmente, desacredite el mito popular de que el petróleo es la causa de esta ley de maldad.

El tema de la caída de sándwiches no persigue al público en general ni a los investigadores. Durante décadas, se han llevado a cabo experimentos, se han filmado películas, se han escrito artículos, un sándwich caído cubierto de leyendas y conclusiones incorrectas. Pocas tareas sin valor atrajeron tanta atención, y si crees que todo esto es mimos, entonces ten en cuenta que incluso los premios tampoco son serios para su solución. En 1995, Robert Matthews recibió el Premio Shnobel por su trabajo, "Falling Sandwich, Murphy's Law, and Fundamental Constants", publicado en el European Journal of Physics. A pesar del tema cómico y la reacción correspondiente de la comunidad científica, este es un artículo completamente interesante en el que se realiza un análisis exhaustivo del proceso de deslizamiento y se llega a una conclusión de gran alcance: no importa en qué criaturas antropomórficas aparezcan en la atmósfera, estarán condenados a la ley de un sándwich. Después de tal triunfo de la investigación inútil, uno podría cerrar el tema, ¡pero por qué perder la oportunidad de considerar métodos interesantes y objetivamente útiles como ejemplo de un problema interesante!

¡Ida arroja sándwiches en Monte Carlo!

Raramente arrojamos bocadillos como una moneda, al menos cuando envejecemos más de dos años. La mayoría de las veces, repetimos involuntariamente el mismo experimento: un sándwich, originalmente colocado con la mantequilla hacia arriba, se desliza de nuestras manos o se desliza fuera de la mesa. En el proceso de deslizamiento, se retuerce, vuela en el aire y, finalmente, se deja caer sobre la mesa o en el suelo. La etapa inicial de la caída se ve afectada por una serie de parámetros: fricción contra los dedos o la superficie de la mesa, la posición inicial del sándwich y su velocidad inicial, la altura de la caída y, finalmente, el tamaño del sándwich. Tenemos un sistema dinámico con varios parámetros de entrada y una salida: la posición del sándwich en el piso. Dentro del sistema, como en el caso de una moneda, funcionan las leyes mecánicas, que se describen mediante ecuaciones diferenciales y son deterministas . Esto significa que no hay accidente en ellos: el resultado depende solo de los datos de entrada, y con la repetición exacta de los parámetros, deberíamos obtener resultados idénticos. Esto se aplica al modelo de sándwich, presentado en forma de un sistema de ecuaciones diferenciales, pero ¿qué pasa con los sándwiches reales, ásperos y únicos, arrojados por personas reales en restaurantes, en la calle o en el sofá? La variabilidad del mundo real se puede describir aplicando parámetros aleatorios a la entrada del sistema determinista.

Sin embargo, incluso el álgebra de variables aleatorias, que incluye solo la suma y la multiplicación, no es una tarea fácil, ¡pero tenemos ecuaciones diferenciales! No subimos a estas fascinantes áreas silvestres, sino que utilizamos la técnica bien desarrollada en muchas áreas: el método de Monte Carlo . Consiste en acumular estadísticas y en determinar las propiedades de cierto sistema complejo como resultado de pruebas repetidas con varios parámetros aleatorios. Destaco nuevamente: el sistema en estudio no es estocástico ni caótico, y reacciona de manera predecible a los datos de entrada aleatorios. En el método de Monte Carlo, la aleatoriedad solo es necesaria para clasificar eficientemente tantas opciones como sea posible y analizar todos los "ángulos" realistas, obteniendo una idea del comportamiento del sistema.

De hecho, ya hemos usado este método, observando a los ciclistas en una colina y aún lo usaremos organizando una fecha límite en la oficina y compartiendo dinero en una sociedad cerrada. La correspondencia uno a uno entre la probabilidad y la medida del volumen o área, de la que hablamos anteriormente, nos permite utilizar el método de Monte Carlo para la integración numérica. Una característica del próximo experimento de sándwich es que no nos interesará la distribución de probabilidad (exacta o empírica), sino la dependencia de la probabilidad de los parámetros del problema. Buscaremos la respuesta a la pregunta: ¿bajo qué circunstancias se cumple la ley sandwich? Proporcionaremos varios parámetros específicos a la entrada de nuestro sistema dinámico y recopilaremos estadísticas sobre las caídas y bajadas de petróleo. Por lo tanto, el resultado de una serie de experimentos será un número: la probabilidad de una caída de petróleo.

Estoy convencido de que arrojar deliberadamente bocadillos reales en el piso está mal, por lo que utilizaremos modelos matemáticos. Para resolver el problema de la caída de un sándwich, elegí uno de los simuladores del mundo físico disponibles que se utilizan para crear juegos en línea. Permitió crear una mesa virtual y un piso, así como dos sándwiches. Uno apareció en el borde de la mesa, y el segundo "se le escapó de los dedos", es decir, se deslizó de un punto de apoyo. Es mi poder establecer la posición inicial y el ángulo del emparedado, la velocidad horizontal (el caso de romper el emparedado de la mesa), los coeficientes de fricción, el tamaño del emparedado y la altura de la caída. Los experimentos se parecen a esto:

Experimentos con la caída de sándwiches virtuales en un simulador del mundo físico.

En el momento en que el sándwich toca el piso, el ángulo del sándwich es fijo, o más bien, el ángulo del vector normal a él. El signo del seno de este ángulo nos dirá de qué lado se volvió el petróleo: un caso exitoso corresponde a un valor positivo, y una posición hacia abajo corresponde a un valor negativo. El resultado se ingresa en la tabla y el nuevo emparedado virtual está listo para caer. La tarea que establecemos es la siguiente: evaluar la probabilidad de que un sándwich caiga aceite cuando cae desde una altura determinada.

El método de Monte Carlo supone que las variables aleatorias se utilizan como parámetros. Y aquí vale la pena decir algunas palabras sobre qué es una variable aleatoria . Volvamos a los matemáticos y las estructuras matemáticas. ¿Qué estructura se puede usar para simular los resultados de la caída de un número en un dado, o el nivel del agua en un río, porque hay una emoción constante en el agua? ¿Cómo trabajar con la cantidad de autos que pasan la intersección en una hora? ¿Qué estructura puede describir el estado de un electrón? Por un lado, estos son números específicos de un conjunto de valores bien definidos: para un hueso, por ejemplo, de un conjunto $$$\ {1,2,3,4,5,6 \}$ , y este valor es fácil de obtener realizando un experimento. Sin embargo, un segundo experimento dará un resultado diferente, claramente no es solo un número: hoy es uno, mañana es otro. Incluso puede surgir una pregunta filosófica: ¿tiene sentido hablar sobre algún valor exacto del "nivel de agua en el río", o el número de automóviles, porque estos valores no pueden ser "capturados" y registrados? ¿Podría haber, en algún sentido, conocimiento exacto de una variable aleatoria?

A menudo, cuando se habla de tales variables aleatorias, se limitan solo al valor promedio, pero esta es una excelente manera de confundirse o incluso confundirse intencionalmente. Dos números: la media y la desviación estándar, ya son mejores, pero claramente esta no es toda la información sobre el objeto que nos interesa. ¿Quizás estos no son números, sino conjuntos? Digamos, puedes tratar de describir el nivel del agua en el río como un intervalo de valores posibles, teniendo en cuenta la emoción, y por ejemplo con los autos, decir que de 1 a 100 autos pasan en una hora, etc. Pero es fácil ver que el conjunto de valores posibles tampoco es suficiente, por ejemplo, cuando se mide repetidamente el número de autos en la calle, algunos números ocurrirán con mayor frecuencia, y algunos no esperaremos en absoluto. En el último capítulo, presentamos una medida de probabilidad como una función en un espacio de probabilidad. Para una cantidad aleatoria, los eventos elementales de este espacio serán los elementos de su dominio de definición, y la medida determina la distribución de probabilidad para esta cantidad. Y ahora esta es información exhaustiva y precisa. Una función puede representarse analíticamente o como una aproximación por otra función, en forma de tabla, histograma o en forma de gráfico. Todas estas representaciones son modelos del mismo objeto, una variable aleatoria, y lo más importante aquí no es tanto el tipo específico de representación como las propiedades matemáticas de esta función. Para las distribuciones de probabilidad, las propiedades son diferentes: el número de parámetros, el número de modos, entropía, divisibilidad infinita, aditividad, estabilidad, integrabilidad, etc. Al modelar una variable aleatoria desconocida obtenida del experimento, las estadísticas de un enorme arsenal de distribuciones conocidas con propiedades definidas con precisión, selecciona no tanto la función "más similar", sino más bien una función que coincide más completamente en sus propiedades con la variable aleatoria observada. Esta es la esencia del análisis estadístico y las técnicas para probar hipótesis estadísticas que son familiares para todos los estudiantes que han tocado las estadísticas.

Ahora tenemos un problema, en cierto sentido, todo lo contrario. Necesitamos establecer los parámetros del emparedado con variables aleatorias, sin tener datos estadísticos, sino guiados por las propiedades necesarias de estas cantidades. Esta es una parte importante e interesante del método de Monte Carlo, del cual dependen tanto la solución como su corrección.

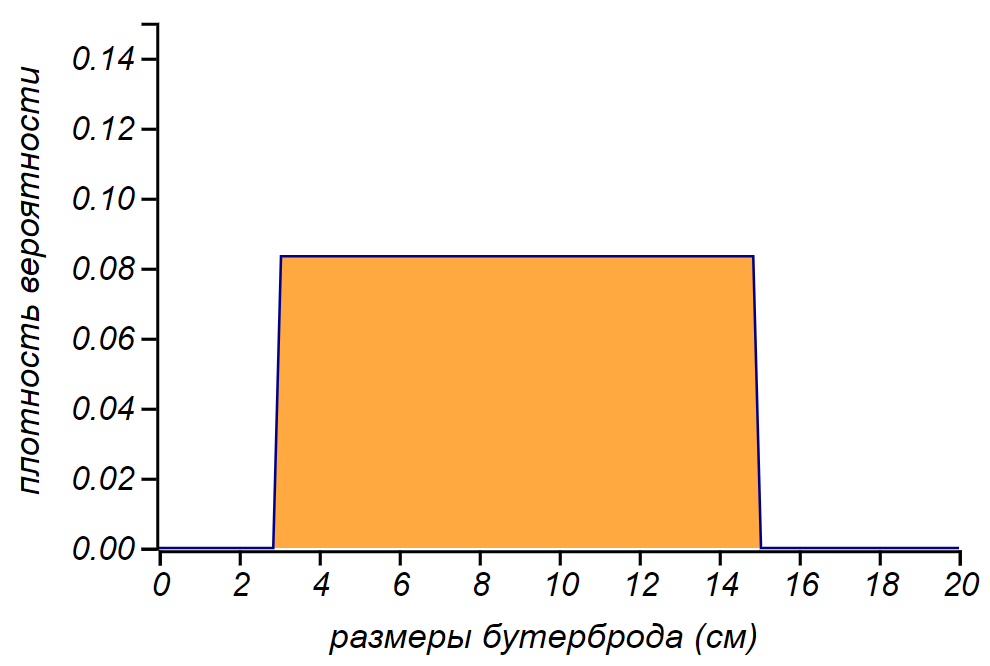1. Las dimensiones del sandwich. Que pueden ser Los canapés de tamaño razonable tienen un centímetro $$$3$ de ancho, y un buen estudiante "bast" puede ser centímetros $$$15$ . Muy a menudo, los sándwiches tienen tamaños de $$$6$ antes $$$10$ ver. En este caso, la probabilidad de encontrar un emparedado de milímetro o metro de ancho, en un sentido práctico, es cero. No puedo decir nada más sobre sándwiches y aceptaré el tamaño de los sándwiches distribuidos uniformemente en el rango especificado. La elección es imperfecta, sin embargo, encontramos sándwiches normales con más frecuencia que los pequeños o gigantes. Pero luego veremos que este punto débil puede ser burlado con gracia.

2. Posición inicial. Aquí, sin más preámbulos, estableceremos una distribución uniforme para mover el emparedado sobre el borde de la mesa, si solo cae.

3. El coeficiente de fricción. Esta es una cantidad adimensional, que depende solo del material. Las mesas y los manteles son diferentes, los dedos exprimen un sándwich con diferentes fuerzas. Rango de coeficiente de $$$0.01$ antes $$$0.5$ , mientras que los valores extremos son poco probables, en promedio, puede esperar algo $$$0.3$ . Cualquier distribución asimétrica en forma de campana de un valor no negativo, por ejemplo, una distribución gamma o un log-normal, nos ayudará.

4. Velocidad inicial. Raramente lanzamos sándwiches a alta velocidad, y la mayoría de las veces no los tiramos, pero sucede, sin embargo. Todo lo que se sabe sobre la magnitud de la velocidad es que es positiva y se puede suponer que al deslizar, en promedio, nos movemos como manos promedio, es decir, a una velocidad de aproximadamente $$$0.5$ m / s Si solo se conoce esto sobre una cantidad, entonces es razonable describirlo por una distribución exponencial (por eso, hablaremos más adelante cuando aprendamos sobre la entropía de las distribuciones). Su modo es cero, por lo que la proporción de sándwiches que cayeron sin una gran velocidad inicial será bastante decente. En la "cola" habrá sándwiches, lanzados inadvertidamente al vuelo cuando se sacan las migajas de la mesa.

5. Arreglaremos la altura de la mesa, tiraremos cien sándwiches, contaremos la cantidad de aceite caído y lo colocaremos en la mesa, o reflejaremos la probabilidad de la altura en el gráfico.

Estas son las probabilidades de dejar caer un sándwich con mantequilla:

La probabilidad de que los sandwiches de aceite lleguen a diferentes sandwiches con diferentes condiciones dependiendo de la altura de la caída. Para cada altura $$$100$ pruebas

Se observa cierta tendencia, pero se ha producido una propagación muy amplia. Al promediar, resulta que la probabilidad de la altura de caída es casi independiente y apenas supera la mitad. ¿Puedes confiar en tal experimento? ¿Refuta la ley de un sándwich? Tal vez no arrojamos suficientes sándwiches, ¡había tanta información ruidosa! Aumentemos el número de lanzamientos y veamos qué sucede:

La probabilidad de que un aceite caiga en varios sándwiches calculada para un mayor número de pruebas (500 para cada altura).

Hay menos emisiones, pero es aún más claramente visible que la ley del sándwich es muy, muy débil. ¿Pero realizamos nuestros experimentos correctamente? El método de Monte Carlo parece atractivo y simple: conócete a ti mismo sustituyendo datos horribles y observa qué sucede. La matemática es una cosa honesta: qué tipo de pregunta está lista para dar qué tipo de respuesta . Pero si esta respuesta tiene sentido depende de la pregunta.

Antes de comenzar los experimentos, no como un juguete como el nuestro, sino real y costoso, utilizando un satélite en órbita, un acelerador de partículas o un millar de sándwiches reales con aceite, es necesario llevar a cabo un trabajo preparatorio. Y una de las formas poderosas y hermosas de comprender cómo llevar a cabo un experimento correctamente es analizar las dimensiones del problema.

Modelamos un emparedado por coordenadas generalizadas, momentos y fuerzas, cantidades físicas, que, a su vez, están conectadas por ecuaciones de mecánica analítica. En física, las cantidades cuantitativas con las que tratamos, que medimos y sustituimos en las ecuaciones, no "encajan" en números ordinarios; tienen una estructura adicional, que se llama dimensión . No todas las expresiones matemáticas correctas tienen sentido si las cantidades dimensionales participan en ellas. Digamos que no tiene sentido agregar velocidad y masa, es imposible comparar la fuerza y ​​la distancia. Sin embargo, podemos considerar el producto de la velocidad y la masa, habiendo recibido una nueva cantidad dimensional: el momento o el momento; es posible cuadrar la velocidad y dividir por la distancia, obteniendo así un valor que tiene la dimensión de aceleración.

El análisis de dimensiones y la teoría de similitud nacieron hace mucho tiempo, desde la época de Lord Rayleigh. Se utilizan en mecánica, electrodinámica, astrofísica y cosmología, lo que permite abordar tareas complejas con una elegancia aterradora. Sin embargo, la investigación en esta área no se ha completado y una definición rigurosa de la estructura formada por cantidades cuantitativas (dimensionales) fue dada solo en 2016 por el matemático español Álvaro Raposo.

Las limitaciones impuestas por las dimensiones en las fórmulas físicas a menudo son percibidas por los alumnos y estudiantes como un desastre adicional que necesita ser monitoreado. Pero, por otro lado, ¡las restricciones lógicamente consistentes son extremadamente útiles! Filtran expresiones incorrectas, le permiten "predecir" la estructura de la solución de un problema físico antes de su solución detallada, son una herramienta poderosa para planificar y analizar datos experimentales.

Pero eso es interesante. Calculamos la caída del sándwich en el programa, utilizando números no dimensionales sino ordinarios. ¿Cómo se puede "borrar" una cantidad física de una dimensión y convertirla en un número? Para este propósito, estamos familiarizados con las unidades familiares de medida de cantidades físicas: todos estos metros, libras, minutos y Newtons. Las unidades de medida toman la parte dimensional de la cantidad, dejándonos con un factor, un número real, que una computadora ya puede manejar. Por ejemplo, la velocidad en la dirección seleccionada es $$$60$ km / h puede ser representado por el número $$$60$ . Pero hay una sutileza: la representación numérica depende de la elección de las unidades de medida. Si selecciona otras unidades (por ejemplo, metros y segundos) , la misma velocidad estará representada por un número diferente: $$$16.7$ . Los números son diferentes, pero la cantidad es uno y no depende de nuestra elección de unidades.

Surge la pregunta: ¿hay en algún sentido un "mejor" sistema de unidades? Resulta que, para esto, al resolver el problema, es necesario utilizar las cantidades dimensionales incluidas en el problema como unidades de medida.

En este capítulo, tenemos sándwiches volando, en las monedas voladoras anteriores, damos un ejemplo más volador. ¿Cómo deben compararse las cualidades de vuelo de las diferentes aves? Está claro que las velocidades que desarrollan las aves son diferentes: para una paloma: $$$90$ km / h, a la velocidad - $$$140$ km / h, para grúas, gorriones o patos silvestres - $$$50$ km / h, colibrí - $$$80$km / h Pero todas estas aves varían significativamente en tamaño y forma de vuelo. Si la longitud de un loro se mide en loros, y el tiempo se mide en períodos de aleteo de sus alas, puede obtener algo de velocidad propia , como dicen . Puede dividir las velocidades que estas aves pueden desarrollar en valores propios y obtener una velocidad sin dimensiones que muestre cuánto tiempo puede viajar el cuerpo en una solapa de las alas. Aquí está el resultado de esta comparación:

el pajaro	velocidad, km / h	longitud del cuerpo	frecuencia de barrido, 1 / s	velocidad propia, m / s	velocidad adimensional
veloz	140	18 cm	5 5	0.9	43
paloma mensajera	90	30 cm	5 5	1,5	17
colibrí	80	8 cm	200	16	1.4
grua	50	1 m	2,5	2,5	5 5
ánade real	50	40 cm	9 9	3.6	3.8
gorrión	46	12 cm	13	1,6	8

Se puede ver que el veloz es legítimamente considerado el mejor volador, pero el colibrí consume energía de manera ineficiente, sin embargo, este pájaro no tiene la tarea de volar durante mucho tiempo, como una paloma. Las mismas velocidades absolutas de la grúa, el gorrión y el pato difieren significativamente cuando se traducen en cantidades adimensionales. Este tipo de cálculo se utiliza para simular un avión realmente grande, probando un modelo pequeño en un túnel de viento. Si todos los parámetros adimensionales de estos dos sistemas están cerca, pueden considerarse físicamente similares y el modelado tiene sentido. Ya hemos usado este enfoque, reflejando unidades relativas en lugar de las absolutas en los diagramas de Lorenz. Esto nos permitió comparar entre sí varios fenómenos y distribuciones.

Está claro cuál será el sistema de unidades más adecuado al analizar el vuelo de un emparedado. Por supuesto, la longitud debe medirse en sándwiches. Por una unidad de tiempo, podemos tomar el valor$$$\sqrt{l/g}$ donde $$$l$ - la longitud del sándwich, y $$$g$- aceleración de la gravedad. Y la altura de la mesa no debe medirse en metros, sino en sus propias unidades. Una vez obtenido el resultado, podemos generalizarlo inmediatamente tanto en el caso de los canapés como en un sólido "zapato de bastón". Entonces, repetimos los cálculos, pero en el gráfico reflejamos la altura de la tabla en unidades relativas. Si hicimos todo bien, entonces para dos emparedados de diferentes tamaños, deberíamos obtener gráficos muy similares. Veamos esto:

La probabilidad de que un sándwich de aceite llegue a un determinado valor fijo, a diferentes alturas de incidencia, calculado en unidades relativas. Los puntos azules corresponden a un sándwich con un tamaño de 5 cm, los puntos rojos corresponden a 10 cm.

En la formulación inicial, clasificamos a través de varios tamaños y recibimos una nube de resultados en los que la dependencia de interés para nosotros estaba oculta. Con un aumento en el número de pruebas, promediamos esta nube y recibimos una respuesta poco interesante. Para mostrar más claramente en qué consistió el error metodológico, imagine que queremos calcular la probabilidad de que un sándwich se caiga, mirando al azar las condiciones y tamaños iniciales del sándwich y la altura. Esto es equivalente a promediar todos los resultados que obtuvimos a la vez. Como resultado, obtenemos un punto medio seguro, una probabilidad muy cercana a$$$1/2$como tirar una moneda! Este es un resultado muy lógico y esperado, pero es completamente poco interesante. Al promediar una gran cantidad de datos para diferentes tamaños, ya estamos cerca de esta conclusión. Pero si el propósito del modelado es identificar patrones, tiene sentido minimizar el número de parámetros.

Los datos borrados ahora hablan claramente a favor de la ley de la mezquindad, limitando, sin embargo, a un cierto rango de alturas:$$$2$ antes $$$6$ el tamaño del sándwich (desde la altura del codo sobre la mesa hasta la altura de los brazos de una persona de pie). Fuera de este rango, el sándwich tiene una mayor probabilidad de girar el lado derecho antes de caerse.

Pero, ¿qué pasa si miras más y arrojas sándwiches por la ventana? Está claro que cuando cae desde una gran altura, no importa de qué lado caiga en lo que se convertirá el sándwich, y la resistencia del aire estabiliza la caída, pero en teoría, ¿qué esperamos ver? Probablemente, se deben observar algunas fluctuaciones en la probabilidad a medida que aumenta el tiempo de vuelo. A ver:
La probabilidad de que un sándwich de aceite aterrice al caer desde una altura alta.

Adivinamos con la frecuencia, pero es curioso que la amplitud disminuya y las fluctuaciones de probabilidad converjan a $$$0.5$ . ¿De qué puede hablar? ¿Es este el mismo efecto que en el caso de una moneda, cuando con un aumento en la duración del vuelo las consecuencias de las desviaciones de las condiciones iniciales se vuelven más significativas? Resulta que en este caso la naturaleza de la igualación de probabilidades es diferente.

Un poco más de análisis dimensional

No importa cuán frívolo sea el tema de nuestro libro, hablamos el lenguaje de las matemáticas y él se esfuerza por encontrar soluciones exactas. El método de Monte Carlo nos permitió tener una idea de la solución, pero eso fue lo que se llama fuerza bruta. Esto no es tan interesante como al menos algunos, sino una solución analítica. Un análisis de las dimensiones nos permitirá obtener una forma teórica de la dependencia obtenida por el método de Monte Carlo. Para esto, no necesitamos resolver ecuaciones diferenciales; además, todas nuestras consideraciones no van más allá de los límites de relaciones completamente primitivas y obvias. Este es el encanto del análisis dimensional, que, sin embargo, a veces parece un truco. Entonces, comencemos, restringiéndonos por simplicidad a solo deslizar un sándwich de longitud $$$l$ de la mesa de altura $$$H$ con velocidad horizontal cero

1. El ángulo de rotación del sándwich descendente depende del tiempo y la velocidad angular:

$$

$$\ varphi = t \ omega.$$

2. La velocidad angular es igual al producto del tiempo de deslizamiento y la aceleración angular:

$$

$$\ omega = t_0 \ varepsilon.$$

3. El tiempo de deslizamiento se puede expresar en términos de la aceleración de la gravedad y parte de la longitud del emparedado que entró en contacto con la mesa en la siguiente proporción:

$$

$$t_0 \ propto \ sqrt {\ frac {l_0} {g}}.$$

Aqui $$$l_0$ - la longitud del sándwich sobre la mesa. Aquí usamos la relación de proporcionalidad indicada por el signo $$$\ propto$ . Expresión $$$y \ propto x$ puede ser reemplazado por $$$y = C x$ donde $$$C$ - alguna constante desconocida. Realmente amo esta actitud. La proporcionalidad "incorpora" todo lo complicado que se convierte en una constante: tanto el hecho de que el momento de gravedad cambia durante la rotación como el centro de rotación cambia cuando se desliza. Todo esto, por supuesto, necesita saberlo para un cálculo preciso, pero el resultado es solo un coeficiente adimensional, y en nuestro análisis no juega un papel importante. Con un icono, nos salvamos de la tediosa integración.

4. La aceleración angular se produce a partir de la aceleración de la gravedad y depende del hombro al que se aplica la gravedad:

$$

$$\ varepsilon \ propto \ frac {g} {l-l_0}.$$

Y de nuevo la señal $$$\ propto$ nos permitió no calcular el momento de inercia de la placa para el eje que yace en su plano, así como la proyección cambiante de la gravedad (estas son dos integrales más).

5. Finalmente, el tiempo de caída depende de la altura de la mesa y la aceleración de la gravedad:

$$

$$t \ propto \ sqrt {\ frac {H} {g}}.$$

6. Sustituyendo todas estas expresiones en la primera fórmula, obtenemos un resultado simple:

$$

$$\ varphi \ propto \ sqrt {\ frac {l_0 H} {l (l-l_0)}},$$

que, si mides todas las longitudes en los emparedados, se convierte en

$$

$$\ varphi \ propto \ sqrt {\ frac {x h} {1-x}}.$$

Aqui $$$l_0 = x l$ y $$$H = h l$ . Bueno, todo converge: el ángulo es adimensional y depende de coeficientes adimensionales. Este ángulo no depende de la escala de tiempo; queda geometría pura. El denominador no es peligroso cuando $$$x> 0.5$ el sándwich no caerá en absoluto (estamos considerando la velocidad horizontal cero), entonces $$$0 <x <0.5$ .

De qué lado caerá el sándwich está determinado por el signo del seno del ángulo $$$\ varphi$ es decir, función $$$\ mathrm {sign} (\ sin \ varphi)$ . Esta función regresa $$$-1$ para el caso de "oil up" y $$$1$ para "aceite abajo". Podemos usar esta función para expresar la probabilidad de que un sándwich determinista se caiga si lo llevamos a un rango de $$$0$ antes $$$1$ :

$$

$$P _ {\ downarrow} (x, h) = \ frac12 \ left [1+ \ mathrm {sign} (\ sin \ varphi) \ right] = \ frac12 \ left \ {1+ \ mathrm {sign} \ left [ \ sin \ left (C \ sqrt {\ frac {xh} {1-x}} \ right) \ right] \ right \},$$

donde la flecha indica simbólicamente la posición del aceite. Coeficiente $$$C$ que aparece en la fórmula de probabilidad expresa todo lo que permanece oculto con la ayuda del signo proporcional. De hecho, fue un movimiento muy complicado, nos salvó de la tediosa integración (e incluso de tres), pero ¿cómo sabemos ahora a qué equivale este coeficiente? Además, del experimento, ¡un solo experimento para medir el ángulo en el momento de la caída es suficiente para obtener una estimación de este valor! Usando el simulador, encontré fácilmente que $$$C = 2.3$ .

La siguiente tarea es expresar matemáticamente cuáles son las posiciones iniciales $$$x$ puede ser diferente Estamos interesados ​​en la probabilidad de que un sándwich caiga mantequilla si $$$x$ será igual $$$0.2$ o $$$0.4$ o cualquier número de $$$0$ antes $$$0.5$ . Utilizamos la unión "o", y cada uno de estos casos es considerado por nosotros como independiente y excluye a todos los demás en un experimento específico. Recuerde que la probabilidad es una medida del espacio de probabilidad, y si es así, entonces la probabilidad es aditiva. Esto nos permite simplemente agregar las probabilidades $$$P _ {\ downarrow} (x, h)$ , para todos los valores $$$x$ , multiplicando desde antes por la probabilidad de caer en un rango específico de valores. Rompemos el segmento de $$$0$ antes $$$0.5$ en $$$n$ partes y calcule la estimación de probabilidad en forma de suma:

$$

$$P _ {\ downarrow} (h) \ sim \ frac {2} {n} \ sum \ limits_ {i = 0} ^ n P _ {\ downarrow} \ left (\ frac {i} {2n}, h \ right ),$$

aquí está el multiplicador $$$2 / n$ expresa probabilidad para una variable aleatoria $$$x$ entrar en un pedazo de ancho $$$1 / n$ . Así es como se ve el resultado para un número significativo de particiones ( $$$n = 100$ ) y una serie de experimentos numéricos con velocidad horizontal cero:

Evaluación teórica y experimental de la probabilidad de que un aceite descargue un sándwich cuando cae desde una gran altura. La velocidad horizontal inicial en los experimentos es cero.

La solución que presentamos anteriormente contiene más parámetros aleatorios, por lo que resultó ser más suave y cercano a $$$0.5$ . Pero, en principio, el análisis dimensional puede llevarse a cabo para un caso más general.

Tenga en cuenta que la probabilidad $$$P _ {\ downarrow}$ acercándose con el aumento $$$h$ a valores cercanos a $$$0.5$ . Y esto no se debe en absoluto a la incertidumbre e influencia de los errores iniciales. Los cálculos mostraron que este es el resultado de sumar los muchos armónicos formados por los valores $$$x$ al sumar $$$P _ {\ downarrow} (x, h)$ . Si nos olvidamos del desafortunado sándwich y continuamos el horario $$$P _ {\ downarrow}$ , entonces vemos que la estimación de probabilidad continuará fluctuando tan cerca $$$0.5$ , luchando gradualmente por este valor.

¿Es posible descubrir sin cálculos directos si la probabilidad continuará convergiendo a $$$0.5$ o alguna vez volverá a crecer? Y en este fenómeno también hay un lugar para las matemáticas no triviales y profundas. El hecho es que cada valor $$$x$ corresponde una cierta frecuencia de oscilaciones, y todo el conjunto forma el llamado espectro de la función total. Si el espectro es discreto, es decir, consiste en frecuencias separadas, entonces la función total (se llama transformada de Fourier) será periódica. A un espectro continuo en forma de una constante en un segmento de $$$0$ antes $$$0.5$ corresponderá una función aperiódica correspondiente a oscilaciones menguantes. Pero buscamos una nueva rama de las matemáticas: el análisis funcional .

El gran Enrico Fermi, el abuelo del método de Montecarlo (se considera que el matemático Stanislav Ulam es el padre), enseñó a sus alumnos a realizar evaluaciones simples, descifrar un pedazo de papel o dedos, que esperamos obtener antes de proceder con la solución exacta del problema. Es maravilloso que si la evaluación resulta ser correcta, quedará claro que se capta la esencia del problema; de lo contrario, este es el resultado más útil, ¡eso significa que la tarea resultó ser más interesante de lo que parece!

En nuestro caso, una simple estimación es suficiente; el problema del sándwich no merece una solución más completa. El método de Monte Carlo nos mostró solo indicios de la solución, y el análisis dimensional mostró solo algo de su estructura general, pero juntos podrían mostrarnos cómo funciona la probabilidad deseada. La erudición le permite al matemático ver estructuras preparadas en los planos de la solución y hacer suposiciones y conclusiones de gran alcance.

Robert Matthews, en su estudio histórico, también utilizó el análisis dimensional para mostrar que la ley sandwich es fundamental. Su conclusión se basa en el hecho de que la altura máxima de un organismo que se ha adherido a las extremidades posteriores con el objetivo de tomar las extremidades anteriores para tomar un emparedado con aceite está determinada por las propiedades de resistencia de los tejidos biológicos y la gravedad. A su vez, el tamaño característico del sándwich debe corresponder a la escala de la criatura, y los enanos en algún planeta pesado y los dylds en un planeta con baja gravedad elegirán sándwiches de tamaño propio. Aquí llegamos a lo que se llama especulación en la ciencia. Esto no es una reventa de ningún bien a precios exorbitantes, sino suposiciones dudosas que forman la base de una construcción lógica. En particular, suponemos que las criaturas tienen manos que tienen proporciones similares a las nuestras, y esto es más que discutible.

Sobre petróleo y viento

En merfología, la cita incorrecta de la ley de X.L. Grupo Menka:

Los problemas complejos siempre tienen soluciones simples, fáciles de entender e incorrectas.

A menudo se puede escuchar que la ley del sándwich tiene la culpa del petróleo, que es más denso que el pan y, por lo tanto, "supera". Y aunque esto no se aplica al tema de nuestro libro, quiero analizar esta pregunta para ponerle fin. Para que luego cualquiera pueda referirse al hecho de que "¡los científicos han demostrado que la presencia de petróleo no afecta a qué lado golpea el emparedado!"

Cuando era niño, nos divertía arrojando una mosca de la paloma o una pluma de cola, clavada en un pedazo de plastilina, de un centímetro o dos de diámetro, en lo alto. Voló hasta cuatro metros, después de lo cual descendió bella y suavemente en rotación automática, como un helicóptero con un motor amortiguado. Luego crecimos y nuestra diversión se volvió menos inofensiva. Adquirimos una tuerca y atornillamos dos pernos en ella desde lados opuestos, comprimiendo el relleno de las cabezas de fósforo aplastadas. Quedaba por atar una cinta o simplemente un trozo de cuerda a uno de los pernos, desenroscar adecuadamente y correr hacia el cielo durante quince metros. En el otoño, una cinta ligera estabilizó la posición vertical del proyectil, proporcionando un impacto de alta calidad en el asfalto y una pequeña explosión, a veces rompiendo la tuerca en pedazos. (¡Tenga cuidado si decide compartir esta experiencia de la infancia con sus hijos!)

En ambos experimentos, vemos que una pluma o cinta ligera apareció rápidamente sobre la parte pesada del aparato y estabilizó la caída. Esto, aparentemente, lleva a una opinión intuitiva de que la mantequilla pesada y el pan ligero también deberían comportarse de esta manera. Imagine un globo: una canasta más densa siempre se encuentra debajo de un globo menos denso. Además, la experiencia sugiere que si agarras con dos dedos el centro geométrico de un objeto con una masa distribuida asimétricamente, entonces caerá para que la parte pesada quede en la parte inferior.

Pero ambos fenómenos no funcionan en el caso de un sándwich que cae.

Comencemos con el segundo proceso, con "pesaje". No fue una casualidad que especifique aburridamente: "... si adoptas el punto medio geométrico de un objeto ...", significa que los puntos de tangencia se encuentran en una cierta línea recta que forma el eje de rotación que pasa por el centro de gravedad del objeto. En este caso, de hecho, una posición estable será aquella en la que el centro de gravedad esté debajo del eje. Pero si el eje de rotación formado por los dedos pasa a través del centro de gravedad, entonces el sistema estará en equilibrio indiferente, no le importará cómo está orientado.

¿Qué hace que una pluma con un peso pequeño, una bomba de una nuez o un globo con globos en una cesta te hagan navegar de la manera "correcta"? Aire Él "sostiene" nuestros objetos para que el eje pase por encima del centro de gravedad. Más precisamente, una corriente de aire que se aproxima que crea una fuerza distribuida sobre el área del cuerpo. Y el punto condicional de aplicación de esta fuerza se ubicará cerca del centro geométrico del cuadrado de la figura. Para hacerlo más claro, dibujaremos las fuerzas que actúan sobre el globo condicional, como en un objeto con una densidad desigual:

Las fuerzas que llevan el globo a una posición estable.

¿Qué tal un sándwich?

En primer lugar, si "apagamos" el aire, simplemente se caerá. En caída libre, el cuerpo gira precisamente alrededor del centro de masa, por lo que no tiene ninguna razón para girar de ninguna manera especial. Como dicen en la escuela: "En un ascensor que cae, se observa la ingravidez". La mantequilla en el sándwich es igual de ingrávida.

El aceite denso puede afectar el proceso de deslizamiento, elevará efectivamente el centro de masa por encima del toque exacto y cambiará la expresión para la aceleración angular $$$l$ en $$$\ sqrt {l ^ 2 + d ^ 2} = l \ sqrt {1+ \ delta ^ 2}$ donde $$$\ delta = d / l$ - el grosor relativo del sándwich. Para valores pequeños $$$\ delta$ esta expresión se puede calcular como $$$l (1+ \ delta ^ 2/2)$ . Obtenemos, como dicen, un efecto de segundo orden. Para un sándwich con una relación de ancho a espesor como $$$5$ a $$$1$ , los cambios relativos no exceden $$$2 \%$ . ¡Y este es el límite superior máximo del efecto, porque elevamos el centro de masa al grosor del sándwich, que corresponde a un aceite infinitamente denso!

Ahora volvemos a encender el aire, dejando la densidad del aceite infinitamente más alta que la densidad del pan. Tenemos una placa delgada y densa con un paracaídas liviano pero resistente al aire. Mientras el plano del sándwich es horizontal más o menos, el momento de las fuerzas de resistencia del aire proporcional a la acción del viento sobre él, el área con la que interactúa el flujo de aire: $$$M _ {-} \ propto l ^ 2$ . En la posición vertical, el viento disminuirá y, en consecuencia, el momento será diferente: $$$M_ {|} \ propto l d$ . La relación de estos puntos: $$$M_ {|} / M _ {-} \ propto \ delta.$ Escribí un signo proporcional aquí, ya que los coeficientes de resistencia para una placa ubicada a través y a lo largo del flujo son diferentes, y son desconocidos para mí. Pero no son necesarios: ya está claro que el efecto del aire en una posición vertical (es decir, hace que la posición del aceite sea desigual) es más débil que en una horizontal. Y ahora recordamos que el sándwich gira, lo que significa que es sustituido por el flujo por el final o por el plano. Podemos introducir una medida de la acción de las fuerzas de resistencia. Si la velocidad angular de rotación no cambia significativamente en un período (y este es el caso del aire), entonces tiene sentido tomar como medida el cambio en el momento angular proporcional al tiempo de la fuerza. A su vez, el período de acción es proporcional al ángulo "barrido" por el emparedado durante este período. Como resultado, medidas de momentos de acción. $$$M_ {|}$ y $$$M _ {-}$ será proporcional $$$M_ {|} \ varphi_ {|}$ y $$$M _ {-} \ varphi _ {-}$ donde los ángulos que barren el extremo y el plano se muestran en el dibujo. 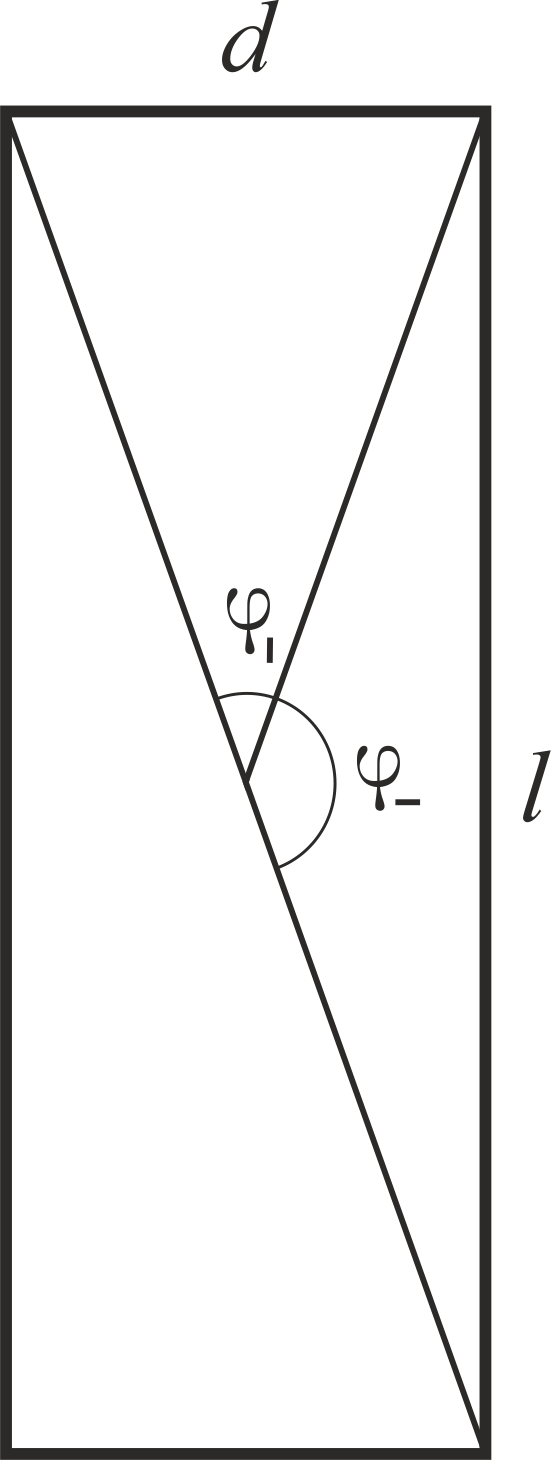Podríamos utilizar el trabajo de las fuerzas de resistencia como medida y obtener la misma proporción. La relación de ángulo es fácil de calcular:

$$

$$\ frac {\ varphi_ {|}} {\ varphi _ {-}} = \ frac {\ varphi_ {|}} {\ frac {\ pi} {2} - \ varphi_ {|}}.$$

En pequeño $$$d / l$ , $$$\ varphi_ {|} \ sim \ delta$ (usamos la propiedad de la tangente de un ángulo pequeño $$$10 \%$ precisión en ángulos menos $$$30 ^ \ circ$ ), y por lo tanto, tenemos:

$$

$$\ frac {M_ {|} \ varphi_ {|}} {M _ {-} \ varphi _ {-}} \ sim \ delta \ frac {\ delta} {\ frac {\ pi} {2} - \ delta} \ propto \ delta ^ 2. $$$

Nuevamente, resulta que el efecto de la asimetría para un emparedado plano está limitado por el efecto de segundo orden. Típicamente, la densidad de la mantequilla es solo el doble que la del pan, y el centro del desplazamiento de masa no excede un tercio del grosor del sándwich con una capa razonable de mantequilla que no exceda el grosor del pan. Esta observación reducirá el efecto del petróleo a $$$0.2 \%$ .

Si le pareció al lector que ahora estábamos disparando a los gorriones del arma, entonces estoy completamente de acuerdo con él. Pero, en primer lugar, no quiero escuchar más sobre el petróleo "que supera", en segundo lugar, no quiero ser infundado, y en tercer lugar, quería mostrar cómo el físico estima las cantidades, representando el proceso, pero sin tener datos completos. Por supuesto, al momento del aterrizaje, la mantequilla puede adherirse al piso y evitar que el sándwich salte y se vuelque nuevamente, pero ciertamente no desarmaré la mecánica del impacto, la deformación elástica y el salto de un pedazo de pan. Así que salió mucho análisis para este problema. Y el segundo Shnobelevskaya para ella ya no se dará.

$$

$$* * *$$

El objetivo de nuestro camino no era tan importante: la refutación o justificación de la ley del sándwich, como el camino mismo. Mostró cómo la combinación de diferentes métodos matemáticos le permite ver el problema desde diferentes ángulos y proporciona un conocimiento bastante preciso, incluso sin una solución detallada del problema. La consistencia de varias disciplinas matemáticas, enfoques y puntos de vista es la fuerza y ​​la belleza de las matemáticas. Es apropiado recordar las maravillosas palabras de Marina Tsvetaeva: "No quiero tener un punto de vista, quiero tener vista" . El estudio de varias áreas de las matemáticas puede proporcionar al investigador una visión multidimensional "volumétrica" ​​real, que le permite mirar en el espacio aparentemente cerrado y oculto del conocimiento.