👇🏿 🚶 📤 Redes de densidad de mezclas 👩🏾‍🎤 🌇 🔔

Hola a todos!

Hablemos, como habrás adivinado, de las redes neuronales y el aprendizaje automático. Por el nombre está claro lo que se dirá sobre las redes de densidad de mezcla, luego solo MDN, no quiero traducir el nombre y dejarlo como está. Sí, sí, sí ... habrá un poco aburrido de matemática y teoría de la probabilidad, pero sin ella, desafortunadamente o afortunadamente, depende de ti decidir si es difícil imaginar el mundo del aprendizaje automático. Pero me apresuro a tranquilizarte, será relativamente pequeño y no será muy difícil. De todos modos, puede omitirlo, pero solo mire una pequeña cantidad de código en Python y PyTorch, es cierto, escribiremos la red usando PyTorch, así como varios gráficos con los resultados. Pero lo más importante es que habrá una oportunidad de comprender un poco y comprender qué son las redes de MD.

Bueno, empecemos!

Regresión

Para empezar, refresquemos un poco nuestro conocimiento y recordemos, brevemente, qué es la regresión lineal .

Tenemos un vector

X = \ {x_1, x_2, ..., x_n \}

$X = \ {x_1, x_2, ..., x_n \}$ necesitamos predecir el valor

Y

$Y$ , que de alguna manera depende de

X

$X$ usando algún modelo lineal:

h a t Y = X^{T} h a t b e t a

$\ hat {Y} = X ^ T \ hat {\ beta}$

Como función de error, usaremos el error al cuadrado:

S E (b e t a) = s u m_{i = 1}^{n} (y_{i} - h a t y_{i})^{2} = s u m_{i = 1}^{N} (y_{i} - x_{i}^{T} h a t b e t a)^{2}

$SE (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 = \ sum_ {i = 1} ^ N (y_i-x_i ^ T \ hat {\ beta} ) ^ 2$

Este problema se puede resolver directamente tomando la derivada de SE y estableciendo su valor en cero:

f r a c d e l t a S E (b e t a) d e l t a b e t a = 2 X^{T} (m a t h b f y - X b e t a) = 0

$\ frac {\ delta SE (\ beta)} {\ delta \ beta} = 2X ^ T (\ mathbf {y} -X \ beta) = 0$

Por lo tanto, simplemente encontramos su mínimo, y SE es una función cuadrática, lo que significa que el mínimo siempre existirá. Después de eso, ya puedes encontrar fácilmente

b e t a

$\ beta$ :

h a t b e t a = (X^{T} X)^{- 1} X^{T} m a t h b f y

$\ hat \ beta = (X ^ TX) ^ {- 1} X ^ T \ mathbf {y}$

Eso es todo, el problema está resuelto. Aquí es donde terminamos de recordar qué es la regresión lineal.

Por supuesto, la dependencia inherente a la naturaleza de la generación de datos puede ser diferente y luego ya debe agregarse algo de no linealidad a nuestro modelo. Resolver el problema de regresión directamente para datos grandes y reales también es una mala idea, ya que existe una matriz

X^{T} X

$X ^ TX$ dimensiones

n v e c e s n

$n \ veces n$ , y uno todavía necesita encontrar su matriz inversa, y a menudo sucede que tal matriz simplemente no existe. En este caso, nos ayudan varios métodos basados en el descenso de gradiente. La no linealidad de los modelos se puede implementar de varias maneras, incluido el uso de redes neuronales.

Pero ahora, hablemos no sobre esto, sino sobre las funciones de error. ¿Cuál es la diferencia entre SE y Log-Likelihood cuando los datos pueden tener una relación no lineal?

Nos ocupamos del zoológico, a saber: OLS, LS, SE, MSE, RSS

Todo esto es uno y lo mismo en esencia, RSS - suma residual de cuadrados, OLS - mínimos cuadrados ordinarios, LS - mínimos cuadrados, MSE - error cuadrático medio, SE - error cuadrático. En diferentes fuentes puedes encontrar diferentes nombres. La esencia de esto es solo una: desviación cuadrática . Puedes confundirte, por supuesto, pero te acostumbras rápidamente.

Vale la pena señalar que MSE es la desviación estándar, un cierto valor promedio del error para todo el conjunto de datos de entrenamiento. En la práctica, generalmente se usa MSE. La fórmula no es particularmente diferente:

M S E (b e t a) = f r a c 1 N s u m_{i = 1}^{n} (y_{i} - h a t y_{i})^{2}

$MSE (\ beta) = \ frac {1} {N} \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2$

N

$N$ - el tamaño del conjunto de datos,

h a t y_{i}

$\ hat {y} _i$ - predicción del modelo para

y_{i}

$y_i$ .

Basta! ¿Probabilidad? Esto es algo de la teoría de la probabilidad. Así es, es pura teoría de la probabilidad. Pero, ¿cómo puede relacionarse la desviación cuadrática con la función de probabilidad? Y cómo resulta. Está relacionado con encontrar la máxima verosimilitud (Máxima verosimilitud) y con una distribución normal, para ser más precisos, con su promedio

m u

$\ mu$ .

Para darse cuenta de que esto es así, veamos nuevamente la función de desviación cuadrada:

R S S (b e t a) = s u m_{i = 1}^{n} (y_{i} - h a t y_{i})^{2} q q u a d q q u a d (1)

$RSS (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 \ qquad \ qquad (1)$

Ahora suponga que la función de probabilidad tiene una forma normal, es decir, una distribución gaussiana o normal:

L (X) = p (X | t h e t a) = p r o d^{X} m a t h c a l N (x_{i}; m u, s i g m a^{2})

$L (X) = p (X | \ theta) = \ prod ^ X \ mathcal {N} (x_i; \ mu, \ sigma ^ 2)$

En general, cuál es la función de probabilidad y cuál es el significado de la misma, no lo diré, puede leer sobre ella en otro lugar, también debe familiarizarse con el concepto de probabilidad condicional, el teorema de Bayes y mucho más, para una comprensión más profunda. Todo esto entra en la teoría pura de la probabilidad, que se estudia tanto en la escuela como en la universidad.

Ahora, recordando la fórmula de distribución normal, obtenemos:

L (X; m u, s i g m a^{2}) = p r o d^{X} f r a c 1 s q r t 2 p i s i g m a^{2} e^{- f r a c (x_{i} - m u)^{2} 2 s i g m a^{2}} q q u a d q q u a d (2)

$L (X; \ mu, \ sigma ^ 2) = \ prod ^ X \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {(x_i- \ mu) ^ 2} {2 \ sigma ^ 2}} \ qquad \ qquad (2)$

¿Qué pasa si ponemos la desviación estándar

s i g m a^{2} = 1

$\ sigma ^ 2 = 1$ y elimine todas las constantes en la fórmula (2), simplemente elimine, no reduzca, porque encontrar el mínimo de la función no depende de ellas. Entonces veremos esto:

L (X; m u, s i g m a^{2}) s i m p r o d^{X} e^{- (x_{i} - m u)^{2}}

$L (X; \ mu, \ sigma ^ 2) \ sim \ prod ^ Xe ^ {- (x_i- \ mu) ^ 2}$

Todavía nada como? No? Bueno, ¿y si tomamos el logaritmo de la función? Del logaritmo, en general, hay algunas ventajas: la multiplicación se convertirá en una suma, un grado en multiplicación y

l o g e = 1

$\ log {e} = 1$ - para esta propiedad vale la pena aclarar que estamos hablando del logaritmo natural y, estrictamente hablando

l n e = 1

$\ ln {e} = 1$ . Y en general, el logaritmo de una función no cambia su máximo, y esta es la característica más importante para nosotros. La conexión con Log-Likelihood y Likelihood y por qué esto será útil se describirá a continuación en una pequeña digresión. Y entonces, lo que hicimos: eliminamos todas las constantes y tomamos el logaritmo de la función de probabilidad. También eliminaron el signo menos, convirtiendo así la probabilidad de registro en probabilidad de registro negativa (NLL), la conexión entre ellos también se describirá como una bonificación. Como resultado, obtuvimos la función NLL:

l o g L (X; m u, I^{2}) s i m s u m (X - m u)^{2}

$\ log L (X; \ mu, I ^ 2) \ sim \ sum (X- \ mu) ^ 2$

Eche otro vistazo a la función RSS (1). Sí, son lo mismo! Exactamente! También se ve que

m u = h a t y

$\ mu = \ hat {y}$ .

Si utiliza la función de desviación estándar de MSE, obtenemos de esto:

o p e r a t o r n a m e a r g m i n M S E (b e t a) s i m o p e r a t o r n a m e a r g m a x m a t h b b E_{X s i m P_{d a t a}} l o g P_{m o d e l} (x; b e t a)

$\ operatorname {argmin} MSE (\ beta) \ sim \ operatorname {argmax} \ mathbb {E} _ {X \ sim P_ {data}} \ log P_ {model} (x; \ beta)$

donde

m a t h b b E

$\ mathbb {E}$ - expectativa matemática

b e t a

$\ beta$ - parámetros del modelo, en el futuro los denominaremos como:

t h e t a

$\ theta$ .

Conclusión: Si la familia LS se usa como una función de error en la pregunta de regresión, entonces esencialmente resolvemos el problema de encontrar la función de máxima verosimilitud en el caso en que la distribución es gaussiana. Y el valor predicho

h a t y

$\ hat {y}$ igual al promedio en la distribución normal. Y ahora sabemos cómo está conectado todo esto, cómo la teoría de probabilidad (con su función de probabilidad y distribución normal) y los métodos de desviación estándar u OLS están conectados. Se pueden encontrar más detalles sobre esto en [2].

Y aquí está el bono prometido. Como estamos hablando de las relaciones entre las diversas funciones de error, consideraremos (no necesariamente para ser leídas):

La relación entre Cross-Entropy, Likelihood, Log-Likelihood y Negative Log-Likelihood

Supongamos que tenemos datos

X = \ {x_1, x_2, x_3, x_4, ... \}

$X = \ {x_1, x_2, x_3, x_4, ... \}$ , cada punto pertenece a una clase específica, por ejemplo

\ {x_1 \ rightarrow1, x_2 \ rightarrow2, x_3 \ rightarrow n, ... \}

$\ {x_1 \ rightarrow1, x_2 \ rightarrow2, x_3 \ rightarrow n, ... \}$ . Total allí

n

$n$ clases, mientras que ocurre la clase 1

c_{1}

$c_1$ veces, clase 2 -

c_{2}

$c_2$ tiempos y clase

n

$n$ -

c_{n}

$c_n$ tiempos Sobre estos datos entrenamos algún modelo

t h e t a

$\ theta$ . La función de verosimilitud (verosimilitud) se verá así:

P (d a t o s | t h e t a) = P (0, 1, . . ., n | t h e t a) = P (0 | t h e t a) P (1 | t h e t a) . . . P (n | t h e t a)

P (1 | t h e t a) P (2 | t h e t a) . . . P (n | t h e t a) = p r o d^{c_{1}} h a t y_{1} p r o d^{c_{2}} h a t y_{2} . . . p r o d^{c_{n}} h a t y_{n} = h a t y_{1}^{c_{1}} h a t y_{2}^{c_{2}} . . . h a t y_{n}^{c_{n}}

$P (1 | \ theta) P (2 | \ theta) ... P (n | \ theta) = \ prod ^ {c_1} \ hat {y} _1 \ prod ^ {c_2} \ hat {y} _2 ... \ prod ^ {c_n} \ hat {y} _n = \ hat {y} _1 ^ {c_1} \ hat {y} _2 ^ {c_2} ... \ hat {y} _n ^ {c_n}$

donde

P (n | t h e t a) = h a t y_{n}

$P (n | \ theta) = \ hat {y} _n$ - probabilidad pronosticada para la clase

n

$n$ .

Tomamos el logaritmo de la función de probabilidad y obtenemos Log-Likelihood:

l o g P (d a t o s | t h e t a) = l o g (h a t y_{1}^{c_{1}} . . . h a t y_{n}^{c_{n}}) = c_{1} l o g h a t y_{1} + . . . + c_{n} l o g h a t y_{n} = s u m_{i}^{n} c_{i} l o g h a t y_{i}

$\ log {P (datos | \ theta)} = \ log {(\ hat {y} _1 ^ {c_1} ... \ hat {y} _n ^ {c_n})} = c_1 \ log {\ hat { y_1}} + ... + c_n \ log {\ hat {y_n}} = \ sum_i ^ n {c_i \ log {\ hat {y_i}}}$

Probabilidad

h a t y e n [0, 1]

$\ hat {y} \ en [0, 1]$ se encuentra en el rango de 0 a 1, basado en la definición de probabilidad. Por lo tanto, el logaritmo tendrá un valor negativo. Y si multiplicamos Log-Likelihood por -1 obtenemos la función Negative Log-Likelihood (NLL):

N L L = - l o g P (d a t o s | t h e t a) = - s u m_{i}^{n} c_{i} l o g h a t y_{i}

$NLL = - \ log {P (datos | \ theta)} = - \ sum_i ^ n {c_i \ log {\ hat {y_i}}}$

Si dividimos la NLL por el número de puntos en

X

$X$ ,

N = c_{1} + c_{2} + . . . + c_{n}

$N = c_1 + c_2 + ... + c_n$ entonces obtenemos:

- f r a c 1 N l o g P (d a t a | t h e t a) = - s u m_{i}^{n} f r a c c_{i} N l o g h a t y_{i}

$- \ frac {1} {N} \ log {P (data | \ theta)} = - \ sum_i ^ n {\ frac {c_i} {N} \ log {\ hat {y_i}}}$

Se puede observar que la probabilidad real de la clase

n

$n$ es igual a:

y_{n} = f r a c c_{n} N

$y_n = \ frac {c_n} {N}$ . Desde aquí obtenemos:

N L L = - s u m_{i}^{n} y_{i} l o g h a t y_{i}

$NLL = - \ sum_i ^ n {y_i \ log {\ hat {y_i}}}$

ahora si nos fijamos en la definición de entropía cruzada

H (p, q) = - s u m p l o g q

$H (p, q) = - \ sum {p \ log {q}}$ entonces obtenemos:

N L L = H (y_{i}, h a t y_{i})

$NLL = H (y_i, \ hat {y_i})$

En el caso de que solo tengamos dos clases

n = 2

$n = 2$ (clasificación binaria) obtenemos la fórmula para la entropía cruzada binaria (también puede conocer el conocido nombre Log-Loss):

H (y, h a t y) = - (y l o g h a t y + (1 - y) l o g (1 - h a t y))

$H (y, \ hat {y}) = - (y \ log {\ hat {y}} + (1-y) \ log {(1- \ hat {y})})$

De todo esto, puede entenderse que, en algunos casos, minimizar la entropía cruzada es equivalente a minimizar el NLL o encontrar el máximo de la función de probabilidad (Probabilidad) o Log-Probabilidad.

Un ejemplo Considere una clasificación binaria. Tenemos valores de clase:

y = np.array([0, 1, 1, 1, 1, 0, 1, 1]).astype(np.float32)

Probabilidad real

y

$y$ para la clase 0 es igual

2 / 8 = 0.25

$2/8 = 0.25$ , para la clase 1 es igual

6 / 8 = 0.75

$6/8 = 0.75$ . Supongamos que tenemos un clasificador binario que predice la probabilidad de la clase 0

h a t y

$\ hat {y}$ para cada ejemplo, respectivamente, para la clase 1, la probabilidad es

(1 - h a t y)

$(1- \ hat {y})$ . Tracemos los valores de la función de pérdida de registro para diferentes predicciones

h a t y

$\ hat {y}$ :

En el gráfico puede ver que el mínimo de la función Log-Loss corresponde al punto 0.75, es decir. si nuestro modelo "aprendió" completamente la distribución de los datos de origen,

$\ hat {y} = y$ .

Regresión de la red neuronal

Entonces llegamos a una práctica más interesante. Veamos cómo puede resolver el problema de la regresión utilizando redes neuronales (redes neuronales). Implementaremos todo en el lenguaje de programación Python, para crear una red utilizamos la biblioteca de aprendizaje profundo PyTorch.

Generación de datos fuente

Datos de entrada

m a t h b f X i n m a t h b b R^{N}

$\ mathbf {X} \ in \ mathbb {R} ^ N$ generar usando una distribución uniforme, tomar el intervalo de -15 a 15,

m a t h b f X e n U [- 15, 15]

$\ mathbf {X} \ en U [-15, 15]$ . Puntos

m a t h b f Y

$\ mathbf {Y}$ obtenemos usando la ecuación:

m a t h b f Y = 0.5 m a t h b f X + 8 s i n (0.3 m a t h b f X) + r u i d o q q u a d q q u a d (3)

$\ mathbf {Y} = 0.5 \ mathbf {X} + 8 \ sin (0.3 \ mathbf {X}) + ruido \ qquad \ qquad (3)$

donde

r u i d o

$ruido$ Es un vector de ruido de dimensión

N

$N$ obtenido utilizando la distribución normal con parámetros:

m u = 0, s i g m a^{2} = 1

$\ mu = 0, \ sigma ^ 2 = 1$ .

Generacion de datos

 N = 3000 #   IN_DIM = 1 OUT_DIM = IN_DIM x = np.random.uniform(-15., 15., (IN_DIM, N)).T.astype(np.float32) noise = np.random.normal(size=(N, 1)).astype(np.float32) y = 0.5*x+ 8.*np.sin(0.3*x) + noise #  3 x_train, x_test, y_train, y_test = train_test_split(x, y) #

El gráfico de los datos recibidos.

Construcción de redes

Cree una red neuronal de avance directo o FFNN.

Building FFNN

 class Net(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=40): super(Net, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.logit = nn.Linear(layer_size, out_dim) def forward(self, x): x = F.tanh(self.fc(x)) #  4 x = self.logit(x) return x

Nuestra red consta de una capa oculta con una dimensión de 40 neuronas y con una función de activación: tangente hiperbólica:

t a n h x = f r a c e^{x} - e^{- x} e^{x} + e^{- x} q q u a d q q u a d (4)

$\ tanh x = \ frac {e ^ x-e ^ {- x}} {e ^ x + e ^ {- x}} \ qquad \ qquad (4)$

La capa de salida es una transformación lineal normal sin una función de activación.

Aprendiendo y obteniendo resultados

Como optimizador usaremos AdamOptimizer. El número de épocas de estudio = 2000, la tasa de aprendizaje (tasa de aprendizaje o lr) = 0.1.

Entrenamiento FFNN

 def train(net, x_train, y_train, x_test, y_test, epoches=2000, lr=0.1): criterion = nn.MSELoss() optimizer = optim.Adam(net.parameters(), lr=lr) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() outputs = net(x_train_var) loss = criterion(outputs, y_train_var) loss.backward() optimizer.step() with torch.no_grad(): x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) outputs = net(x_test_var) test_loss = criterion(outputs, y_test_var) test_losses.append(test_loss.item()) train_losses.append(loss.item()) if i%100 == 0: sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses net = Net() train_losses, test_losses = train(net, x_train, y_train, x_test, y_test)

Ahora veamos los resultados del aprendizaje.

Gráfico de valores de función MSE dependiendo de la iteración del entrenamiento; gráfico de valores para datos de entrenamiento y datos de prueba.

Resultados reales y pronosticados en datos de prueba.

Datos invertidos

Complicamos la tarea e invertimos los datos.

Inversión de datos

 x_train_inv = y_train y_train_inv = x_train x_test_inv = y_train y_test_inv = x_train

Gráfico de datos invertidos.

Para la predicción

m a t h b f h a t Y

$\ mathbf {\ hat Y}$ usemos la red de distribución directa de la sección anterior y veamos cómo maneja esto.

 inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)

Gráfico de valores de función MSE dependiendo de la iteración del entrenamiento; gráfico de valores para datos de entrenamiento y datos de prueba.

Resultados reales y pronosticados en datos de prueba.

Como puede ver en los gráficos anteriores, nuestra red no hizo frente a tales datos, simplemente no puede predecirlos. Y todo esto sucedió porque en un problema tan invertido por un punto

x

$x$ puede corresponder a varios puntos

y

$y$ . Usted pregunta, ¿qué pasa con el ruido? También creó una situación en la que para uno

x

$x$ podría obtener algunos valores

y

$y$ . Sí, eso es correcto. Pero el punto es que, a pesar del ruido, se trataba de una distribución definitiva. Y dado que nuestro modelo esencialmente predijo

p (y | x)

$p (y | x)$ , y en el caso de MSE, fue el valor promedio de la distribución normal (por qué se describe en la primera parte del artículo), luego se ocupó bien de la tarea "directa". De lo contrario, obtenemos varias distribuciones diferentes para uno

x

$x$ y en consecuencia no podemos obtener un buen resultado con solo una distribución normal.

Red de densidad de mezcla

¡Comienza la diversión! ¿Qué es la red de densidad de mezcla (en adelante, red MDN o MD)? En general, este es un cierto modelo que puede simular varias distribuciones a la vez:

p (m a t h b f y | m a t h b f x; t h e t a) = s u m_{k}^{K} p i_{k} (m a t h b f x) m a t h c a l N (m a t h b f y; m u_{k} (m a t h b f x), s i g m a^{2} (m a t h b f x)) q q u a d q q u a d (5)

$p (\ mathbf {y} | \ mathbf {x}; \ theta) = \ sum_k ^ K \ pi_k (\ mathbf {x}) \ mathcal {N} (\ mathbf {y}; \ mu_k (\ mathbf { x}), \ sigma ^ 2 (\ mathbf {x})) \ qquad \ qquad (5)$

Qué fórmula más extraña, dices. Vamos a resolverlo. Nuestra red de MD está aprendiendo a modelar la media

m u

$\ mu$ y varianza

s i g m a^{2}

$\ sigma ^ 2$ para distribuciones múltiples . En la fórmula (5)

p i_{k} (m a t h b f x)

$\ pi_k (\ mathbf {x})$ - los llamados factores de significación de una distribución separada para cada punto

x_{i} i n m a t h b f x

$x_i \ in \ mathbf {x}$ , un determinado factor de mezcla o cuánto contribuye cada una de las distribuciones a un determinado punto. Total allí

K

$K$ distribuciones

Algunas palabras más sobre

p i_{k} (m a t h b f x)

$\ pi_k (\ mathbf {x})$ - de hecho, esto también es una distribución y representa la probabilidad de que para un punto

x_{i} i n m a t h b f x

$x_i \ in \ mathbf {x}$ será una condición

k

$k$ .

Fuh, de nuevo, esta matemática, ya escribamos algo. Y así, comenzaremos a realizar una red. Para nuestra red tomamos

K = 30

$K = 30$ .

 self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance

Defina las capas de salida para nuestra red:

 x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x)

Escribimos la función de error o la función de pérdida, fórmula (5):

 def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses))

Código de compilación MDN completo

 COEFS = 30 class MDN(nn.Module): def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=50, coefs=COEFS): super(MDN, self).__init__() self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance self.out_dim = out_dim self.coefs = coefs def forward(self, x): x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) return pi, mu, sigma_sq #       def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) #   def loss_fn(y, pi, mu, sigma_sq): losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) return loss

Nuestra red de MD está lista para funcionar. Casi listo Queda por entrenarla y ver los resultados.

MDN Training

 def train_mdn(net, x_train, y_train, x_test, y_test, epoches=1000): optimizer = optim.Adam(net.parameters(), lr=0.01) N_EPOCHES = epoches BS = 1500 n_batches = int(np.ceil(x_train.shape[0] / BS)) train_losses = [] test_losses = [] for i in range(N_EPOCHES): for bi in range(n_batches): x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS) x_train_var = Variable(torch.from_numpy(x_batch)) y_train_var = Variable(torch.from_numpy(y_batch)) optimizer.zero_grad() pi, mu, sigma_sq = net(x_train_var) loss = loss_fn(y_train_var, pi, mu, sigma_sq) loss.backward() optimizer.step() with torch.no_grad(): if i%10 == 0: x_test_var = Variable(torch.from_numpy(x_test)) y_test_var = Variable(torch.from_numpy(y_test)) pi, mu, sigma_sq = net(x_test_var) test_loss = loss_fn(y_test_var, pi, mu, sigma_sq) train_losses.append(loss.item()) test_losses.append(test_loss.item()) sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f' %(i, test_loss.item(), loss.item())) sys.stdout.flush() return train_losses, test_losses mdn_net = MDN() mdn_train_losses, mdn_test_losses = train_mdn(mdn_net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)

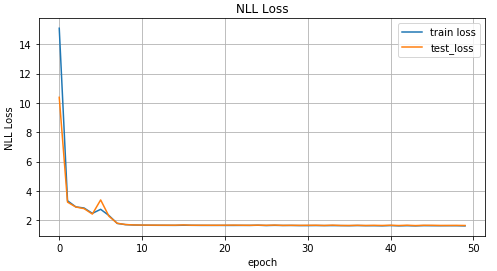
El gráfico de los valores de la función de pérdida dependiendo de la iteración del entrenamiento; el gráfico de valores para los datos de entrenamiento y los datos de prueba.

Como nuestra red ha aprendido los valores medios para varias distribuciones, veamos esto:

 pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv)))

Representa gráficamente los dos valores medios más probables para cada punto (izquierda). Representa gráficamente los 4 valores medios más probables para cada punto (derecha).

Representa gráficamente todos los valores medios para cada punto.

Para predecir datos, seleccionaremos al azar varios valores

m u

$\ mu$ y

s i g m a^{2}

$\ sigma ^ 2$ basado en el valor

p i_{k} (m a t h b f x)

$\ pi_k (\ mathbf {x})$ . Y luego basado en ellos para generar datos objetivo

h a t y

$\ hat {y}$ utilizando distribución normal.

Predicción de resultado

 def rand_n_sample_cumulative(pi, mu, sigmasq, samples=10): n = pi.shape[0] out = Variable(torch.zeros(n, samples, OUT_DIM)) for i in range(n): for j in range(samples): u = np.random.uniform() prob_sum = 0 for k in range(COEFS): prob_sum += pi.data[i, k] if u < prob_sum: for od in range(OUT_DIM): sample = np.random.normal(mu.data[i, k*OUT_DIM+od], np.sqrt(sigmasq.data[i, k])) out[i, j, od] = sample break return out pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) preds = rand_n_sample_cumulative(pi, mu, sigma_sq, samples=10)

Datos pronosticados para 10 valores seleccionados al azar

$\ mu$ y

$\ sigma ^ 2$ (izquierda) y para dos (derecha).

Se puede ver en las cifras que MDN hizo un excelente trabajo con la tarea "inversa".

Usando datos más complejos

Veamos cómo nuestra red de MD maneja datos más complejos, como los datos en espiral. La ecuación de la espiral hiperbólica en coordenadas cartesianas:

x = r h o c o s p h i q q u a d q q u a d q q u a d q q u a d q q u a d q q u a d (6) y = r h o s i n p h i

$x = \ rho \ cos \ phi \\\ qquad \ qquad \ qquad \ qquad \ qquad \ qquad (6) \\ y = \ rho \ sin \ phi \\$

Generación de datos en espiral

 N = 2000 x_train_compl = [] y_train_compl = [] x_test_compl = [] y_test_compl = [] noise_train = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) noise_test = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32) for i, theta in enumerate(np.linspace(0, 5*np.pi, N).astype(np.float32)): #  6 r = ((theta)) x_train_compl.append(r*np.cos(theta) + noise_train[i]) y_train_compl.append(r*np.sin(theta)) x_test_compl.append(r*np.cos(theta) + noise_test[i]) y_test_compl.append(r*np.sin(theta)) x_train_compl = np.array(x_train_compl).reshape((-1, 1)) y_train_compl = np.array(y_train_compl).reshape((-1, 1)) x_test_compl = np.array(x_test_compl).reshape((-1, 1)) y_test_compl = np.array(y_test_compl).reshape((-1, 1))

Gráfico de datos en espiral.

Por diversión, veamos cómo una red de Feed-Forward regular hará frente a tal tarea.

Como se esperaba, la red Feed-Forward no puede resolver el problema de regresión para dichos datos.

Usamos la red de MD creada y descrita anteriormente para capacitarnos en datos espirales.

Mixture Density Network hizo un gran trabajo en esta situación.

Conclusión

Al comienzo de este artículo, recordamos los conceptos básicos de la regresión lineal. Vimos eso en común entre encontrar el promedio para la distribución normal y MSE. Desmontó la conexión entre NLL y la entropía cruzada. Y lo más importante, descubrimos el modelo MDN, que puede aprender de los datos obtenidos de una distribución mixta. Espero que el artículo sea comprensible e interesante, a pesar del hecho de que hubo un poco de matemática.

El código completo se puede ver en GitHub .

Literatura

Redes de densidad de mezcla (Christopher M. Bishop, Grupo de Investigación de Computación Neural, Departamento de Informática y Matemáticas Aplicadas, Universidad de Aston, Birmingham) : el artículo describe completamente la teoría de las redes de MD.
Mínimos cuadrados y máxima probabilidad (MROsborne)

Redes de densidad de mezclas

Regresión

Regresión de la red neuronal

Generación de datos fuente

Construcción de redes

Aprendiendo y obteniendo resultados

Datos invertidos

Red de densidad de mezcla

Usando datos más complejos

Conclusión

Literatura

More articles: