Este es el segundo artículo sobre el análisis y estudio de materiales de la competencia para la búsqueda de barcos en el mar. Pero ahora estudiaremos las propiedades de las secuencias de entrenamiento. Intentemos encontrar información en exceso, redundancia en los datos de origen y eliminarla.

Este artículo también es simplemente el resultado de la curiosidad y el interés ocioso, nada de esto se encuentra en la práctica, y para las tareas prácticas casi no hay nada para copiar y pegar. Este es un pequeño estudio de las propiedades de la secuencia de entrenamiento: se presentan el razonamiento y el código del autor, puede verificar / complementar / cambiar todo usted mismo.
La competencia de búsqueda marina de kaggle ha finalizado recientemente. Airbus propuso analizar imágenes satelitales del mar con y sin barcos. En total, 192555 imágenes 768x768x3: son 340 720 680 960 bytes si uint8 y esta es una gran cantidad de información y había una vaga sospecha de que no se necesitan todas las imágenes para entrenar a la red y en esta cantidad de información la repetición y la redundancia son obvias. Al entrenar una red, es costumbre separar algunos de los datos y no usarlos en el entrenamiento, sino usarlos para verificar la calidad del entrenamiento. Y si uno y el mismo tramo del mar cayeron en dos imágenes diferentes y al mismo tiempo una imagen cayó en la secuencia de entrenamiento y la otra en la secuencia de verificación, entonces la verificación perderá su significado y la red se volverá a entrenar, no verificaremos la capacidad de la red para generalizar la información, porque los datos son los mismos. La lucha contra este fenómeno requirió mucho tiempo y esfuerzo de la GPU de los participantes. Como de costumbre, los ganadores y los ganadores de premios no tienen prisa por mostrar a sus fanáticos los secretos del dominio y el diseño del código, y no hay forma de estudiarlo y aprenderlo, por lo que retomaremos la teoría.
Una simple verificación visual mostró que realmente hay demasiados datos, el mismo tramo del mar cayó en diferentes imágenes, mira los ejemplos




Es por esta razón que no estamos interesados en datos reales, hay muchas dependencias espurias, conexiones innecesarias con nosotros, mal marcado y otras deficiencias.
En el
primer artículo, miramos imágenes con elipses y ruido, y continuaremos estudiándolas. La ventaja de este enfoque es que si encuentra alguna característica atractiva de una red capacitada en un conjunto arbitrario de imágenes, no está claro si se trata de una propiedad de red o de un conjunto de capacitación. Los parámetros estadísticos de las secuencias tomadas del mundo real son desconocidos. Recientemente, el Gran Maestro Pleskov Pavel
paske57 habló sobre cómo a veces es fácil ganar una clasificación de segmentación / clasificación de imágenes si es bueno profundizar en los datos usted mismo, por ejemplo, vea los metadatos de las fotos. Y no hay garantías de que en los datos reales no existan tales dependencias, dejadas involuntariamente. Por lo tanto, para estudiar las propiedades de la red, tomamos imágenes con puntos suspensivos y rectángulos, y determinamos el lugar, el color y otros parámetros usando un generador de números aleatorios de una computadora (que tiene un generador pseudoaleatorio, que tiene un generador basado en otros algoritmos no digitales y propiedades físicas de la sustancia, Pero no discutiremos esto en este artículo).
Entonces, tome el mar
np.random.sample () * 0.75 , no necesitamos olas, viento, costas y otros patrones y caras ocultos. Los barcos / elipses también se pintarán del mismo color, y para distinguir el mar del barco y la interferencia, agregue 0.25 al mar o al barco / jammer, y todos tendrán la misma forma: elipses de diferentes tamaños y orientaciones. La interferencia también será solo rectángulos del mismo color que la elipse; esto es importante, información e interferencia del mismo color contra el fondo del ruido. Solo haremos un pequeño cambio en el color y ejecutaremos
np.random.sample () para cada imagen y para cada elipse / rectángulo, es decir. Ni el fondo ni el color de la elipse / rectángulo se repiten. Además en el texto hay un código del programa para crear imágenes / máscaras y un ejemplo de diez pares seleccionados al azar.
Tome una versión muy común de la red (puede tomar su red favorita) e intente identificar y mostrar la redundancia de una secuencia de entrenamiento grande, para obtener al menos algún tipo de características cualitativas y cuantitativas de redundancia. Es decir El autor cree que muchos gigabytes de secuencias de entrenamiento son sustancialmente redundantes, hay muchas imágenes innecesarias, no hay necesidad de cargar docenas de GPU y hacer cálculos innecesarios. La redundancia de datos se manifiesta no solo y no tanto en el hecho de que las mismas partes se muestran en imágenes diferentes, sino también en la redundancia de información en estos datos. Los datos pueden ser redundantes incluso si no se repiten exactamente. Tenga en cuenta que esta no es una definición estricta de información y su suficiencia o redundancia. Solo queremos saber cuánto puede reducir el tren, qué imágenes puede tirar de la secuencia de entrenamiento y cuántas imágenes son suficientes para un entrenamiento aceptable (estableceremos la precisión nosotros mismos en el programa). Este es un programa específico, un conjunto de datos específico, y es posible que en las elipses con triángulos, como obstáculo, nada funcione tan bien como en las elipses con rectángulos (mi hipótesis es que todo será igual e igual. Pero no lo estamos comprobando ahora) , no realizamos análisis y no probamos teoremas).
Entonces, dado:
- secuencia de aprendizaje de pares imagen / máscara. Podemos generar cualquier número de pares de imágenes / máscaras. Contestaré la pregunta de inmediato: ¿por qué el color y el fondo son aleatorios? Contestaré de manera simple, breve, clara y completa que me gusta tanto, que no se necesita una entidad adicional en forma de borde;
- la red es ordinaria, U-net ordinaria, ligeramente modificada y ampliamente utilizada para segmentación
Idea para probar:
- En la secuencia construida, como en las tareas reales, se utilizan gigabytes de datos. El autor cree que el tamaño de la secuencia de entrenamiento no es tan crítico y que los datos no necesariamente deben ser muchos, pero deben contener "mucha" información. Tal cantidad, diez mil pares de imágenes / máscaras, no es necesaria y la red aprenderá de una cantidad mucho menor de datos.
Comencemos, seleccione 10,000 pares y considérelos cuidadosamente. Exprimiremos toda el agua, todas las partes innecesarias de esta secuencia de entrenamiento y usaremos y pondremos en práctica todos los residuos secos.
Ahora puede probar su intuición y suponer cuántos pares de 10,000 son suficientes para entrenar y predecir otro, pero también creó una secuencia de 10,000 pares con una precisión de más de 0.98. Escriba en una hoja de papel, después de comparar.
Para un uso práctico, tenga en cuenta que tanto el mar como los barcos con interferencia se seleccionan artificialmente, esto es
np.random.sample () .
Cargamos bibliotecas, determinamos los tamaños de una serie de imágenes.import numpy as np import matplotlib.pyplot as plt %matplotlib inline import math from tqdm import tqdm from skimage.draw import ellipse, polygon from keras import Model from keras.optimizers import Adam from keras.layers import Input,Conv2D,Conv2DTranspose,MaxPooling2D,concatenate from keras.layers import BatchNormalization,Activation,Add,Dropout from keras.losses import binary_crossentropy from keras import backend as K import tensorflow as tf import keras as keras w_size = 128 train_num = 10000 radius_min = 10 radius_max = 20
determinar las funciones de pérdida y precisión def dice_coef(y_true, y_pred): y_true_f = K.flatten(y_true) y_pred = K.cast(y_pred, 'float32') y_pred_f = K.cast(K.greater(K.flatten(y_pred), 0.5), 'float32') intersection = y_true_f * y_pred_f score = 2. * K.sum(intersection) / (K.sum(y_true_f) + K.sum(y_pred_f)) return score def dice_loss(y_true, y_pred): smooth = 1. y_true_f = K.flatten(y_true) y_pred_f = K.flatten(y_pred) intersection = y_true_f * y_pred_f score = (2. * K.sum(intersection) + smooth) / (K.sum(y_true_f) + K.sum(y_pred_f) + smooth) return 1. - score def bce_dice_loss(y_true, y_pred): return binary_crossentropy(y_true, y_pred) + dice_loss(y_true, y_pred) def get_iou_vector(A, B):
Usaremos la métrica del
primer artículo . Permítanme recordar a los lectores que vamos a predecir la máscara del píxel: este es el "mar" o "barco" y evaluar la verdad o la falsedad de la predicción. Es decir Son posibles las siguientes cuatro opciones: predijimos correctamente que un píxel es un "mar", predijimos correctamente que un píxel es un "barco" o cometimos un error al predecir un "mar" o un "barco". Entonces, para todas las imágenes y todos los píxeles, estimamos el número de las cuatro opciones y calculamos el resultado; este será el resultado de la red. Y cuanto menos predicciones erróneas y más verdaderas, cuanto más preciso sea el resultado y mejor será la red.
Y para la investigación, tomemos la opción de la bien estudiada U-net, que es una excelente red para la segmentación de imágenes. Se eligió la opción U-net no tan clásica, pero la idea es la misma, la red realiza una operación muy simple con imágenes: reduce la dimensión de la imagen con algunas transformaciones paso a paso y luego intenta recuperar la máscara de la imagen comprimida. Es decir La dimensión de la imagen en nuestro caso se lleva a 16x16 y luego intentamos restaurar la máscara utilizando datos de todas las capas de compresión anteriores.
Examinamos la red como un "recuadro negro", no veremos qué sucede con la red interna, cómo cambian los pesos y cómo se eligen los gradientes: este es el tema de otro estudio.
U-net con bloques def convolution_block(x, filters, size, strides=(1,1), padding='same', activation=True): x = Conv2D(filters, size, strides=strides, padding=padding)(x) x = BatchNormalization()(x) if activation == True: x = Activation('relu')(x) return x def residual_block(blockInput, num_filters=16): x = Activation('relu')(blockInput) x = BatchNormalization()(x) x = convolution_block(x, num_filters, (3,3) ) x = convolution_block(x, num_filters, (3,3), activation=False) x = Add()([x, blockInput]) return x
La función de generar pares de imagen / máscara. En una imagen en color de 128x128 llena de ruido aleatorio con una selección aleatoria de dos rangos, ya sea 0.0 ... 0.75 o 0.25..1.0. Coloca aleatoriamente una elipse orientada aleatoriamente en la imagen y coloca un rectángulo en el mismo lugar. Verificamos que no se crucen y, si es necesario, desplazamos el rectángulo hacia un lado. Cada vez que volvemos a calcular los valores de la coloración del mar / barco. Para simplificar, colocaremos la máscara con la imagen en una matriz, como el cuarto color, es decir. Red.Green.Blue.Mask, es más fácil.
def next_pair(): img_l = (np.random.sample((w_size, w_size, 3))* 0.75).astype('float32') img_h = (np.random.sample((w_size, w_size, 3))* 0.75 + 0.25).astype('float32') img = np.zeros((w_size, w_size, 4), dtype='float') p = np.random.sample() - 0.5 r = np.random.sample()*(w_size-2*radius_max) + radius_max c = np.random.sample()*(w_size-2*radius_max) + radius_max r_radius = np.random.sample()*(radius_max-radius_min) + radius_min c_radius = np.random.sample()*(radius_max-radius_min) + radius_min rot = np.random.sample()*360 rr, cc = ellipse( r, c, r_radius, c_radius, rotation=np.deg2rad(rot), shape=img_l.shape ) p1 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p2 = np.rint(np.random.sample()* (w_size-2*radius_max) + radius_max) p3 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) p4 = np.rint(np.random.sample()* (2*radius_max - radius_min) + radius_min) poly = np.array(( (p1, p2), (p1, p2+p4), (p1+p3, p2+p4), (p1+p3, p2), (p1, p2), )) rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) in_sc_rr = list(set(rr) & set(rr_p)) in_sc_cc = list(set(cc) & set(cc_p)) if len(in_sc_rr) > 0 and len(in_sc_cc) > 0: if len(in_sc_rr) > 0: _delta_rr = np.max(in_sc_rr) - np.min(in_sc_rr) + 1 if np.mean(rr_p) > np.mean(in_sc_rr): poly[:,0] += _delta_rr else: poly[:,0] -= _delta_rr if len(in_sc_cc) > 0: _delta_cc = np.max(in_sc_cc) - np.min(in_sc_cc) + 1 if np.mean(cc_p) > np.mean(in_sc_cc): poly[:,1] += _delta_cc else: poly[:,1] -= _delta_cc rr_p, cc_p = polygon(poly[:, 0], poly[:, 1], img_l.shape) if p > 0: img[:,:,:3] = img_l.copy() img[rr, cc,:3] = img_h[rr, cc] img[rr_p, cc_p,:3] = img_h[rr_p, cc_p] else: img[:,:,:3] = img_h.copy() img[rr, cc,:3] = img_l[rr, cc] img[rr_p, cc_p,:3] = img_l[rr_p, cc_p] img[:,:,3] = 0. img[rr, cc,3] = 1. return img
Creemos una secuencia de entrenamiento de pares, ver al azar 10
_txy = [next_pair() for idx in range(train_num)] f_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) f_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy)
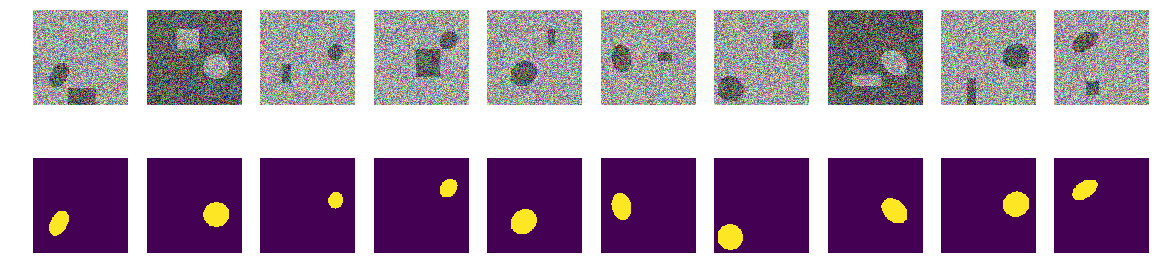
Primer paso Intentemos entrenar en un set mínimo
El primer paso de nuestro experimento es simple, estamos tratando de entrenar a la red para predecir solo 11 primeras imágenes.
batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f_imgs[m0_select>0], f_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0666 : : 47it [00:29, 5.82it/s]Seleccionamos los primeros 11 de la secuencia inicial y capacitamos a la red en ellos. Ahora no importa si la red memoriza estas imágenes específicamente o resume, lo principal es que puede reconocer estas 11 imágenes cuando las necesitemos. Según el conjunto de datos y la precisión seleccionados, la capacitación en red puede durar mucho, mucho tiempo. Pero solo tenemos unas pocas iteraciones. Repito que ahora no es importante para nosotros cómo y qué aprendió o aprendió la red, lo principal es que ha alcanzado la precisión establecida de predicción.
Ahora comienza el experimento principal
Tomaremos nuevos pares de imagen / máscara de la secuencia construida e intentaremos predecirlos por la red entrenada en la secuencia ya seleccionada. Al principio, son solo 11 pares de imagen / máscara y la red está entrenada, quizás no muy correctamente. Si en un nuevo par se predice la máscara de la imagen con una precisión aceptable, entonces descartamos este par, no tiene información nueva para la red, ya lo sabe y puede calcular la máscara a partir de esta imagen. Si la precisión de la predicción es insuficiente, entonces agregamos esta imagen con una máscara a nuestra secuencia y comenzamos a entrenar la red hasta que se obtenga un resultado de precisión aceptable en la secuencia seleccionada. Es decir Esta imagen contiene información nueva y la agregamos a nuestra secuencia de entrenamiento y extraemos la información contenida en ella mediante entrenamiento.
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9830 loss 0.0287 selected img 271 tested img 9949 : : 1563it [14:16, 1.01it/s]
Aquí la precisión se usa en el sentido de "precisión", y no como una métrica estándar de keras, y la subrutina "my_iou_metric" se usa para calcular la precisión. Es muy interesante observar la precisión y el número de imágenes investigadas y agregadas. Al principio, la red agrega casi todos los pares de imágenes / máscaras, y en algún lugar alrededor de 70 comienza a desecharse. Más cerca de 8000 lanza casi todas las parejas.
Verifique los pares visualmente aleatorios seleccionados por la red:
fig, axes = plt.subplots(2, 10, figsize=(20, 5)) t_imgs = f_imgs[m0_select>0] t_msks = f_msks[m0_select>0] for k in range(10): kk = np.random.randint(t_msks.shape[0]) axes[0,k].set_axis_off() axes[0,k].imshow(t_imgs[kk]) axes[1,k].set_axis_off() axes[1,k].imshow(t_msks[kk].squeeze())
Nada especial o sobrenatural:
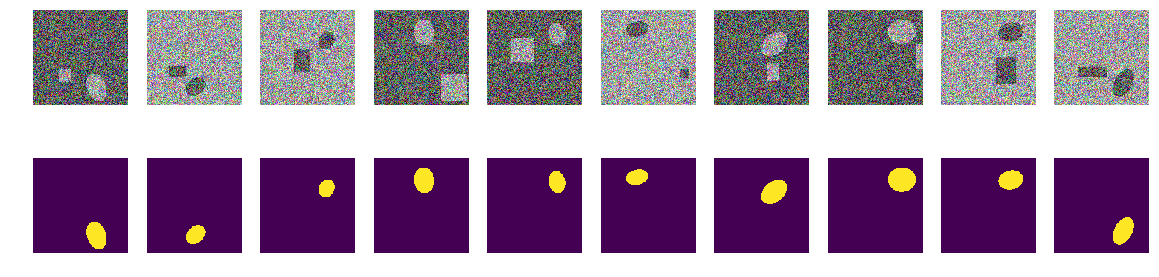
Estos son pares seleccionados por la red en diferentes etapas de entrenamiento. Cuando la red recibió un par de entrada de esta secuencia, no pudo calcular la máscara con la precisión especificada y este par se incluyó en la secuencia de entrenamiento. Pero nada especial, imágenes ordinarias.
Verificación de resultado y precisión
Verificaremos la calidad del programa de entrenamiento de la red, nos aseguraremos de que la calidad no dependa significativamente del orden de la secuencia inicial, para lo cual mezclamos la secuencia inicial de pares de imágenes / máscaras, tomamos los otros 11 primero y de la misma manera, entrenamos la red y cortamos el exceso.
sh = np.arange(train_num) np.random.shuffle(sh) f0_imgs = f_imgs[sh] f0_msks = f_msks[sh] model.compile(loss=bce_dice_loss, optimizer="adam", metrics=[my_iou_metric]) model.summary()
Código de entrenamiento batch_size = 10 val_len = 11 precision = 0.85 m0_select = np.zeros((f_imgs.shape[0]), dtype='int') for k in range(val_len): m0_select[k] = 1 t = tqdm() while True: fit = model.fit(f0_imgs[m0_select>0], f0_msks[m0_select>0], batch_size=batch_size, epochs=1, verbose=0 ) current_accu = fit.history['my_iou_metric'][0] current_loss = fit.history['loss'][0] t.set_description("accuracy {0:6.4f} loss {1:6.4f} ".\ format(current_accu, current_loss)) t.update(1) if current_accu > precision: break t.close()
accuracy 0.8636 loss 0.0710 : : 249it [01:03, 5.90it/s]
batch_size = 50 t_batch_size = 1024 raw_len = val_len t = tqdm(-1) id_train = 0
Accuracy 0.9890 loss 0.0224 selected img 408 tested img 9456 : : 1061it [21:13, 2.16s/it]
El resultado no depende significativamente del orden de pares de la secuencia original. En el caso anterior, la red eligió 271, ahora 408, si lo mezcla, la red puede elegir una cantidad diferente. No revisaremos, el autor cree que siempre habrá sustancialmente menos de 10,000.
Verifique la precisión de la predicción de red en una nueva secuencia independiente
_txy = [next_pair() for idx in range(train_num)] test_imgs = np.array(_txy)[:,:,:,:3].reshape(-1,w_size ,w_size ,3) test_msks = np.array(_txy)[:,:,:,3:].reshape(-1,w_size ,w_size ,1) del(_txy) test_pred_0 = model.predict(test_imgs) t_val_0 = get_iou_vector(test_msks,test_pred_0) t_val_0
0.9927799999999938
Resumen y conclusiones
Entonces, pudimos exprimir menos de trescientos o cuatrocientos seleccionados de 10,000 pares, la precisión de la predicción es 0.99278, tomamos todos los pares que contienen al menos alguna información útil y desechamos el resto. No alineamos los parámetros estadísticos de la secuencia de entrenamiento, agregamos la repetibilidad de la información, etc. y no usó métodos estadísticos en absoluto. Tomamos una imagen que contiene información aún desconocida para la red y exprimimos todo en el peso de la red. Si la red se encuentra con al menos una imagen "misteriosa", lo usará todo en los negocios.
Un total de 271 pares de imágenes / máscaras contienen información para predecir 10,000 pares con una precisión de al menos 0.8075 en cada par, es decir, la precisión total en toda la secuencia es mayor, pero en cada imagen no es menor a 0.8075, no tenemos imágenes que no tengamos podemos predecir y conocemos el límite inferior de esta predicción. (aquí, por supuesto, el autor se jactó, cómo sin esto, el artículo no verifica esta afirmación, alrededor de 0,8075, o evidencia, pero lo más probable es que esto sea cierto)
Para entrenar la red, no hay necesidad de cargar la GPU con todo lo que viene a mano, puede extraer el núcleo del tren y entrenar la red en él como el comienzo del entrenamiento. A medida que obtiene nuevas imágenes, puede marcar manualmente las que la red no pudo predecir y agregarlas al núcleo del tren, volviendo a entrenar la red para extraer toda la información de las nuevas imágenes. Y no es necesario seleccionar una secuencia de validación; podemos suponer que todo lo demás, excepto el seleccionado, es una secuencia de validación.
Una observación matemáticamente más no estricta, pero muy importante. Es seguro decir que cada par de imagen / máscara contiene "mucha" información. Cada par contiene "mucha" información, aunque en la mayoría de los pares de imágenes / máscaras la información se cruza o se repite. Cada uno de los 271 pares de imágenes / máscaras contiene información que es esencial para la predicción, y este par no puede simplemente descartarse.
Bueno, una pequeña observación acerca de los pliegues, muchos expertos y kagglers dividen la secuencia de entrenamiento en pliegues y los entrenan por separado, combinando los resultados obtenidos en otras formas difíciles. En nuestro caso, también puede dividirlo en pliegues, si elimina 271 pares de 10,000, puede crear una nueva secuencia raíz en los restantes, lo que obviamente proporcionará un resultado diferente pero comparable. Simplemente puede mezclar y tomar los otros 11 iniciales, como se muestra arriba.
El artículo proporciona un código y muestra cómo entrenar a U-net para la segmentación de imágenes. Este es un ejemplo concreto, y en el artículo intencionalmente no hay generalizaciones a otras redes, a otras secuencias, no hay matemáticas rigurosas, todo se cuenta y se muestra "con los dedos". Solo un ejemplo de cómo puede aprender la red mientras logra una precisión aceptable.