Genética del cultivar románico: un modelo matemático fractal de expresión génica

¿Qué tienen en común los copos de nieve, la col romanesca, las estrellas de mar, los rayos y los árboles? No lo dirá de inmediato, pero desde un punto de vista matemático, todos estos objetos tienen una característica común: la fractalidad. A los ojos de las matemáticas, todo en nuestro mundo obedece las leyes de la "Reina de las Ciencias". Cualquier fenómeno, proceso u objeto puede expresarse en forma matemática, lo que permite analizarlo desde un nuevo ángulo, por así decirlo. Durante muchos años, los científicos han estado tratando de crear la representación matemática perfecta de los genes, sus relaciones y los procesos en los que están involucrados. Hoy hablaremos sobre cómo los fractales ayudaron a sentar las bases para un modelo matemático completamente nuevo de genes humanos desde la perspectiva del cáncer. ¿Qué es un fractal, por qué es tan importante para los genetistas y matemáticos, y cómo puede un nuevo modelo matemático ayudar a la medicina moderna? Buscaremos respuestas en el informe del grupo de investigación. Vamos

Retiro teórico

Para empezar, vale la pena descubrir brevemente qué es un fractal y con qué se come.

Un fractal es un conjunto con propiedades de autosimilitud. En pocas palabras, cuando algo consiste en varias mini copias de sí mismo.



Los fractales se encuentran en varios fenómenos físicos: desde la difusión hasta la turbulencia. Esto se puede llamar manifestaciones naturales de fractales. La gente también encontró el uso de fractales: en gráficos por computadora, ingeniería de radio, tecnologías de red, etc.

Los fractales son muy coloridos en la película "Doctor Strange" (2016), cuando el Anciano envía al protagonista a una excursión a lo largo de dimensiones paralelas.


Una visión un poco desagradable, pero que demuestra claramente la fractalidad.

Incluso en las estanterías del supermercado puede encontrar manifestaciones de fractalidad, a saber, el ejemplo de col o coliflor romanesco.

Si tenemos en cuenta que hay bastantes tipos de conjuntos con propiedades fractales, se puede argumentar que casi todo lo que nos rodea está relacionado de alguna manera con los fractales. Y el cuerpo humano, especialmente sus genes, no es una excepción. Dado que los fractales se pueden explicar matemáticamente clasificando los componentes, el uso de dicho modelo en genes humanos puede ayudar significativamente a comprender los diversos procesos que ocurren en nuestro cuerpo, incluidas diversas enfermedades, patologías y otras cosas desagradables.

Uno de los procesos más importantes en nuestro cuerpo es la expresión génica (imagen 1a ), cuando la información hereditaria de los genes se transforma en un producto funcional. En otras palabras, nuestras células a través de la expresión génica controlan su estructura y función. Nuestros genes son una base de datos de la cual todas las células del cuerpo obtienen información, realizando las funciones necesarias a partir de entonces. Por lo tanto, nuestra boca no crece pelo, el sistema inmunitario combate infecciones, las células sanguíneas transportan oxígeno, etc. Todos estos procesos ocurren precisamente debido a la programación de las células para realizar tareas específicas, lo que a su vez es posible a través de la síntesis de proteínas a partir de la activación de un gen en particular.


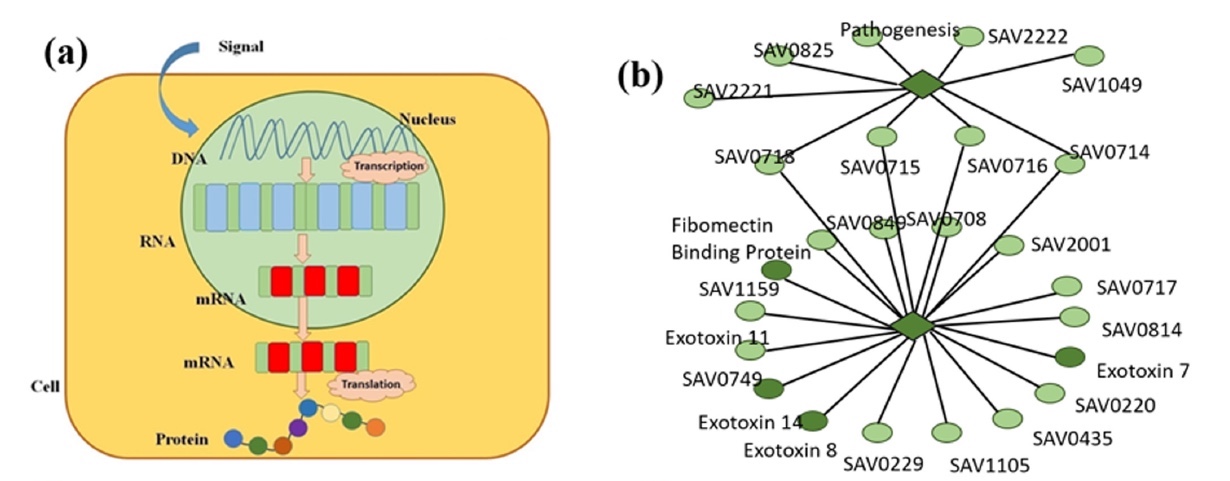Imagen No. 1

La regulación de la expresión génica indica cuándo, cuánto y durante cuánto tiempo se deben producir ciertas proteínas. Por lo tanto, el estudio de este proceso es de gran importancia para una comprensión completa de cómo funcionan ciertos mecanismos de control de organismos.

Este complejo proceso es importante para los científicos, ya que al tener la oportunidad de controlarlo, podrán crear ciertas células sintéticas dotadas de funciones claras, en particular, la entrega de medicamentos contra el cáncer al mismo "corazón" de la enfermedad para un tratamiento más efectivo.

Para mejorar los métodos de tratamiento de tales enfermedades, es necesario aprender el aspecto genético con más detalle. Para hacer esto, los científicos proponen presentar el cuerpo humano en forma de un programa, donde los genes actúan como líneas de código que pueden cambiarse si el programa funciona con falla. Para darse cuenta de esto, primero debe crear un modelo matemático del gen. Por el momento, tales modelos ya existen, pero no pueden ser representativos porque estaban destinados a estudiar la dinámica en la red de genes. En este mismo estudio, que aplicó el concepto de fractales, los científicos decidieron centrarse en el proceso de expresión de un gen en particular, y luego aplicar la correlación cruzada entre pares gen- FT * ( 1b ).

El factor de transcripción (FT) * es una proteína de control de síntesis de ARNm que contiene información sobre la estructura primaria de las proteínas en la matriz de ADN al unirse a sitios de ADN específicos.

En pocas palabras, los científicos decidieron profundizar un poco más, ya que no examinaron toda la "pared" en su conjunto, sino "ladrillos" individuales.

Resultados de la investigación

Los sujetos en este estudio fueron el hongo Saccharomyces cerevisiae (levadura de panadería) y la bacteria Escherichia coli (Escherichia coli).

Al analizar los datos estadísticos de la expresión genética de los sujetos experimentales, se calculó el coeficiente de Hurst * .

El coeficiente de Hurst * es una medida del análisis de series de tiempo.

Series temporales * : un conjunto de datos estadísticos recopilados a diferentes intervalos de tiempo sobre un indicador.

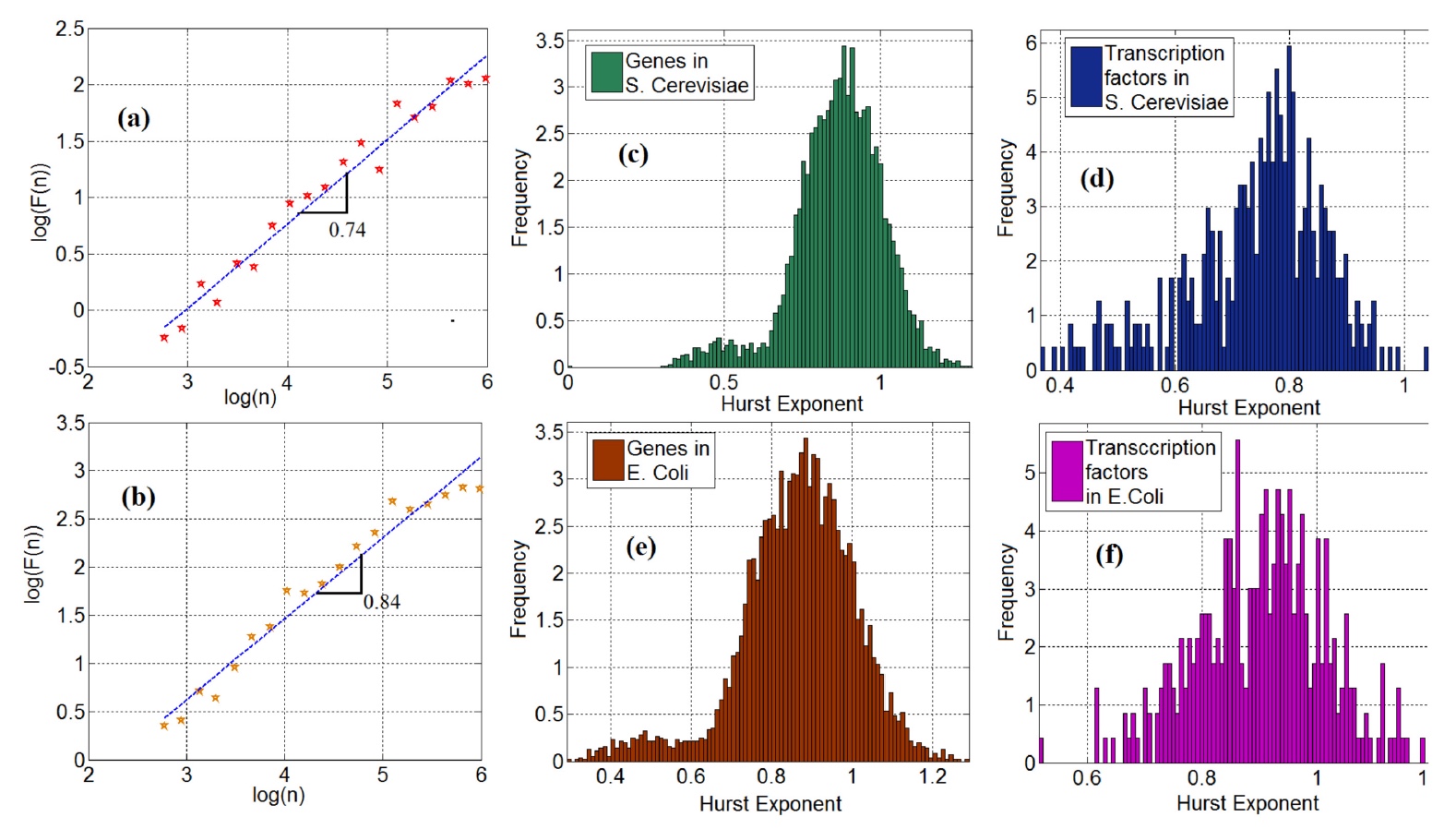Imagen No. 2

Las Figuras 2a (levadura) y 2b (Escherichia coli) muestran gráficos bilogarítmicos * de fluctuaciones en función de la escala de series temporales de FT.

El gráfico bilogarítmico * es un gráfico de datos bidimensionales que utiliza una escala logarítmica en ambos ejes (vertical y horizontal).

La pendiente de la curva en estos gráficos corresponde al coeficiente de Hurst. Vale la pena señalar que el 95% (levadura) y el 98% (bacilo) de las series temporales de genes mostraron dependencia a largo plazo * .

Dependencia a largo plazo * : un indicador en el análisis de series temporales, que indica la atenuación lenta de la dependencia estadística de dos puntos con un aumento en el intervalo de tiempo entre ellos. Está determinado por el indicador de coeficiente de Hurst, de 0 a 1. Si el indicador está por encima de 0.5, entonces tenemos una relación fuerte a largo plazo, por debajo de 0.5, el efecto contrario.

El coeficiente de Hurst de dependencia a largo plazo en este caso particular fue de 0,5, lo que indica su ausencia, en teoría. Sin embargo, un análisis adicional de los datos mostró que este indicador excede un valor de 0.5, lo que indica la presencia de una dependencia a largo plazo de las series de tiempo en la expresión genética ( 2c y 2e ). Esto sugiere que las series temporales del gen FT no pueden considerarse como algo aleatorio, por lo tanto, deben modelarse sobre la base de la cadena de Markov, cuando hay una serie de eventos, la aleatoriedad de cada uno de ellos depende únicamente del evento anterior.

Al igual que los genes, los factores de transcripción también mostraron una relación a largo plazo: al 97% para la levadura y el bacilo (gráficos 2d y 2f ).

Ahora agregue una pizca de análisis fractal al cuenco común. Para empezar, los científicos llaman nuestra atención sobre la bimodalidad de la distribución del coeficiente de Hurst. Esto se ve mejor en los gráficos 2c y 2e. Los científicos explican esta observación por el hecho de que existen procesos de difusión en la expresión génica que tienen varios potenciales de difusión. Por lo tanto, la bimodalidad puede explicarse por el movimiento browniano sin equilibrio con diferentes potenciales. Pero esta declaración requiere evidencia adicional, que los científicos buscarán en los siguientes estudios.

Y ahora volveremos a la multifractalidad. Los científicos utilizaron el análisis multifractal de las fluctuaciones de tendencia para determinar la presencia / ausencia de características multifractales en series temporales de expresión génica. Este análisis mostró la presencia de ambos genes y FT.

Los científicos también aplicaron la metodología bootstrap * para determinar con precisión (más precisamente, para confirmar) la presencia de dependencia a largo plazo, dada la duración limitada de las series temporales experimentales.

Bootstrap * : una técnica para analizar estadísticas de distribuciones de probabilidad.

Para cada serie temporal de expresión génica, se prepararon 10 subintervalos aleatorios, cada uno de los cuales contenía el 90% del fragmento ordenado de la serie temporal inicial. Además, para todas las opciones, se calculó el coeficiente de Hurst. Así, se obtuvo la diferencia entre los indicadores de las series temporales experimentales y las versiones aleatorias. Para E. coli, la diferencia fue solo del 0.006%, y para la levadura de panadería aún menos: 0.0001%. Por lo tanto, se confirmó la presencia de dependencia a largo plazo en ambas muestras.

Después de considerar las características del gen y FT por separado que son de interés, los científicos comenzaron a analizar los pares gen-FT como un solo objeto. El cálculo del índice de correlación cruzada mostró que el 98% de los pares gen-FT (en ambas muestras) poseen las propiedades de dependencia a largo plazo ( 3a ).


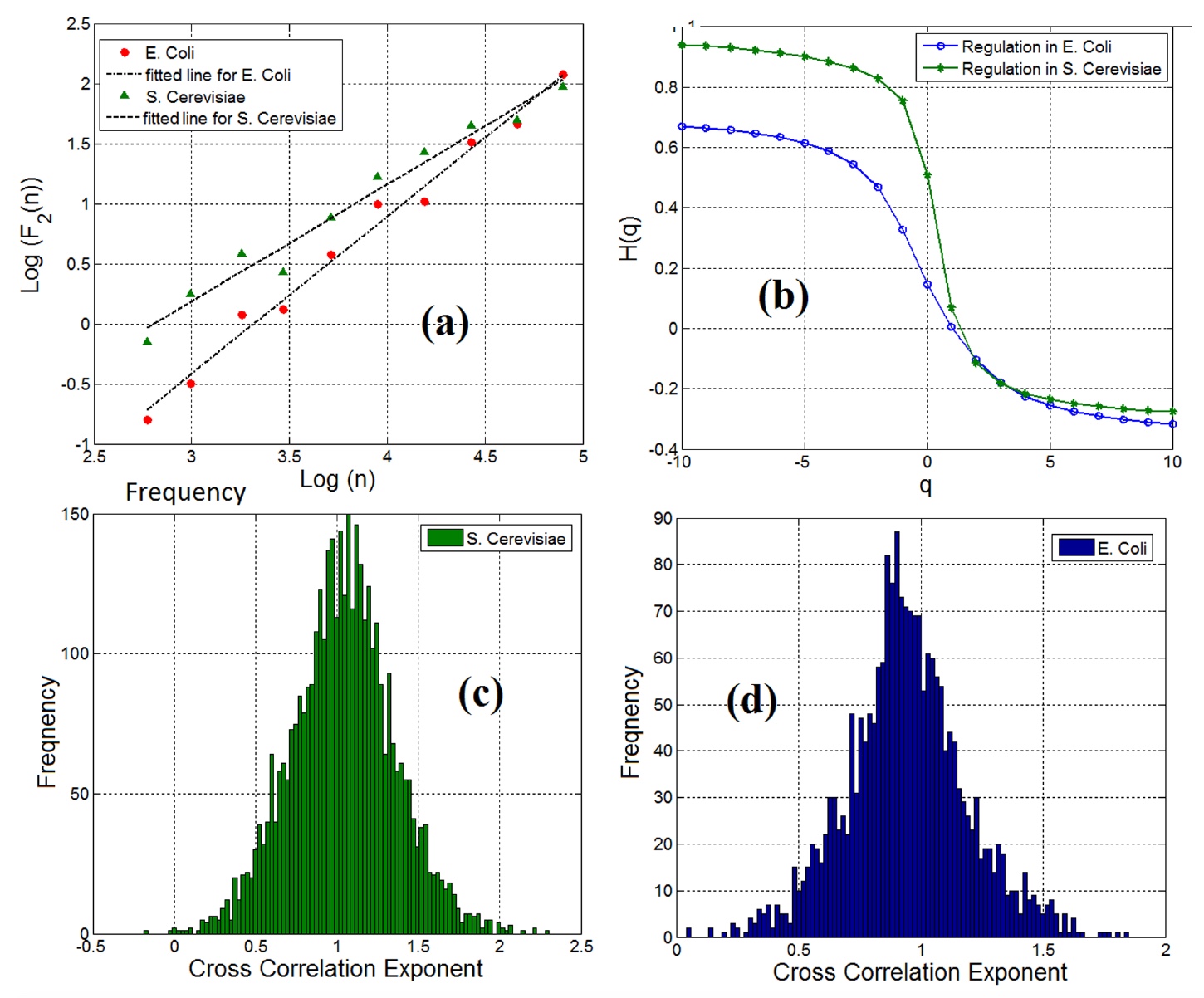Imagen No. 3

Un análisis multifractal de fluctuaciones de tendencia confirmó la presencia de características multifractales en pares gen-FT (gráfico 3b ).

Vale la pena señalar que, independientemente del hecho de que se observaron correlaciones cruzadas tanto fractales como a largo plazo en pares de genes y factores de transcripción en redes de regulación génica, la correlación cruzada no fue la misma para todos los pares. Los gráficos 3c (levadura) y 3d (Escherichia coli) muestran la correlación cruzada de los pares gen-FT.

Los científicos utilizaron estos gráficos para medir la entropía informativa y, como resultado, el contenido informativo de la red de regulación génica para varios tipos de células para el análisis cuantitativo y la especificación de las redes de regulación génica. Los indicadores de entropía fueron: 4.18 - levadura, 5.29 - E. coli. Y esto sugiere que la red de expresión génica en la levadura de panadería es mucho más grande y muestra una dinámica más compleja que la red de expresión génica en Escherichia coli.

Y ahora lo más interesante es la creación de un modelo matemático. Los científicos han elegido dos versiones del modelo: el conjunto de Mandelbrot y el conjunto en forma de árboles diádicos wavelet.

Utilizando los indicadores previamente obtenidos del coeficiente de Hölder en el espectro multifractal, los científicos descubrieron que solo 0.04 de todos los pares de genes FT en la red de regulación de genes de levadura de panadería se pueden modelar usando el conjunto de Mandelbrot. Y en E. coli, este método no puede modelar un solo par.

Si consideramos aquellos pares que pudieron simular, entonces hubo una gran discrepancia en los datos entre el modelo y las observaciones experimentales. Como conclusión, el método de modelado debido al conjunto de Mandelbrot no es adecuado.


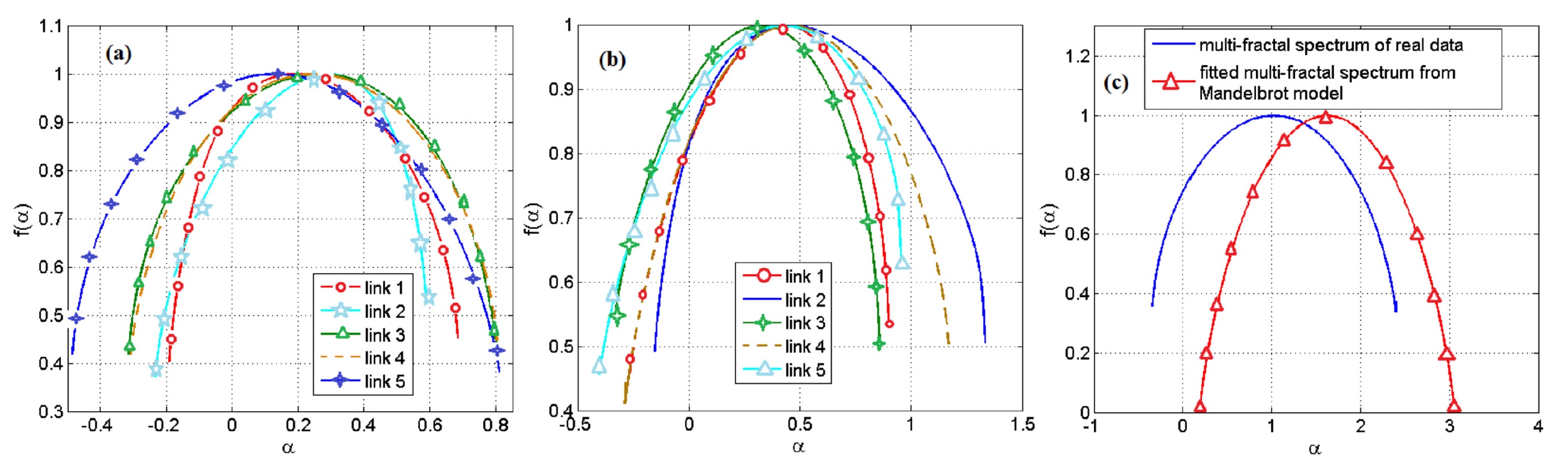Imagen No. 4

Los resultados del uso del modelo basado en el conjunto de Mandelbrot se muestran en los gráficos anteriores. El más brillante es 4c , donde podemos ver cuánto divergen los datos.

Los científicos también compararon la multifractalidad observada de las interdependencias en la red de regulación génica y el modelo multifractal de cascadas aleatorias en árboles wavelet-diádicos.

Los investigadores decidieron verificar si el modelo logarítmico de la cascada W es adecuado para la representación de pares gen-FT en redes de regulación génica. Basado en el espectro empírico y el espectro de singularidades, se calcularon los parámetros de este modelo. A continuación, se hicieron cálculos de las áreas de intersección de los espectros multifractales calculados y empíricos, cuya relación se convirtió en el criterio principal para aceptar o rechazar este modelo matemático multifractal.


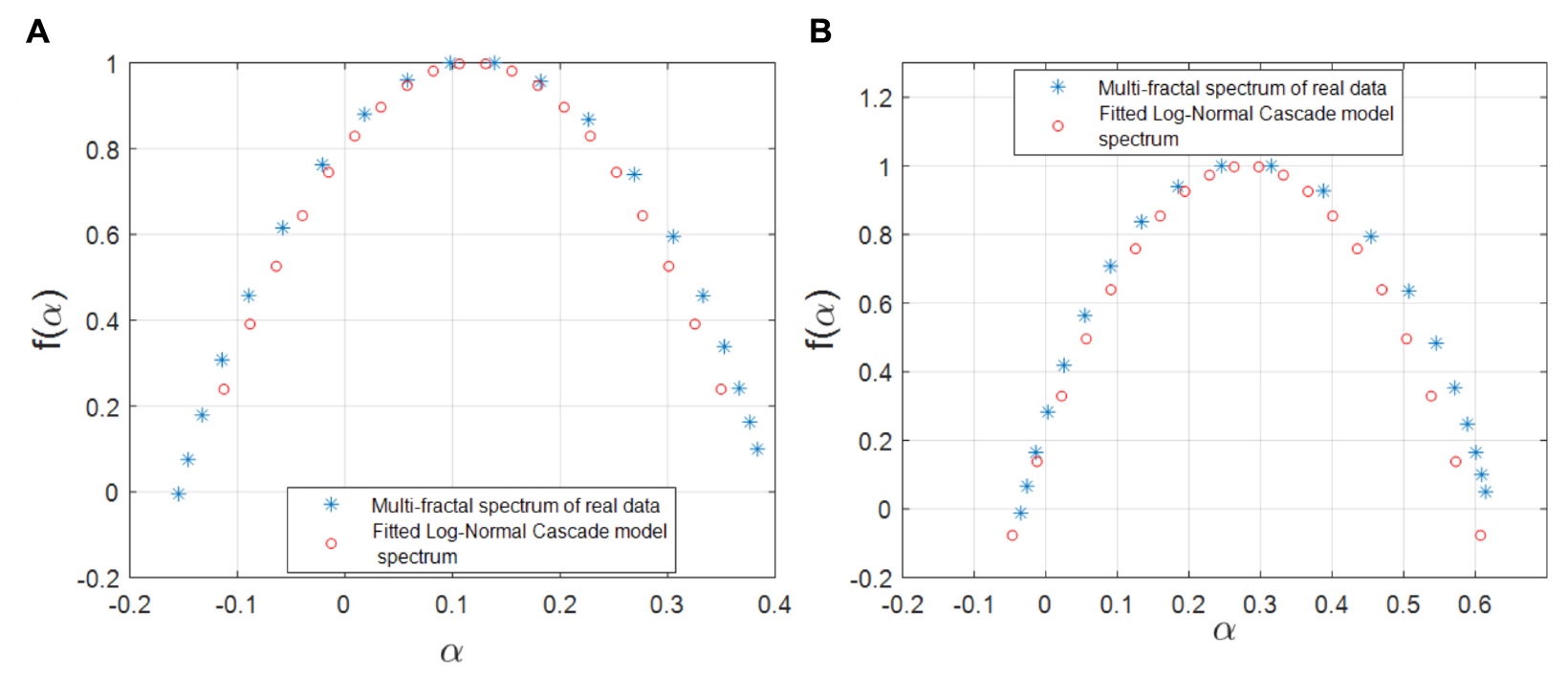Imagen No. 5

Como se puede ver en los gráficos anteriores, que demuestran los espectros multifractales simulados y empíricos, este modelo está casi completamente correlacionado con los datos de observaciones y cálculos realizados anteriormente.

Para conocer más detalladamente los matices del estudio, le recomiendo que consulte el informe del grupo de investigación en este enlace .

Epílogo

Este estudio, en su mayoría teórico, tiene un gran potencial para el uso práctico, ya que ayudó a modelar matemáticamente la red para regular la expresión génica, uno de los procesos más importantes en cualquier organismo vivo. Los procesos complejos son difíciles de entender, no importa cuán extraño suene. Para facilitar la tarea, es necesario dividir el proceso en componentes, elaborar sus "mapas" y seguir la ruta deseada, anotando todas las características y características importantes. El modelado matemático, como nada más, es excelente para esto. Habiendo estudiado el modelo matemático de un objeto o proceso, podemos entender a qué nos enfrentamos antes de continuar con el estudio del objeto o proceso real.

Este estudio confirmó una vez más que no solo la física y la química gobiernan el mundo, sino que las matemáticas están lejos del último lugar en el Olimpo de las ciencias.

Gracias por su atención, sigan curiosos y tengan una excelente semana laboral, muchachos.

Gracias por quedarte con nosotros. ¿Te gustan nuestros artículos? ¿Quieres ver más materiales interesantes? Apóyenos haciendo un pedido o recomendándolo a sus amigos, un descuento del 30% para los usuarios de Habr en un análogo único de servidores de nivel de entrada que inventamos para usted: toda la verdad sobre VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps de $ 20 o cómo dividir el servidor? (las opciones están disponibles con RAID1 y RAID10, hasta 24 núcleos y hasta 40GB DDR4).

VPS (KVM) E5-2650 v4 (6 núcleos) 10GB DDR4 240GB SSD 1Gbps hasta el 1 de enero de forma gratuita si se paga por un período de seis meses, puede ordenar aquí .

Dell R730xd 2 veces más barato? ¡Solo tenemos 2 x Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 TV desde $ 249 en los Países Bajos y los Estados Unidos! Lea sobre Cómo construir un edificio de infraestructura. clase utilizando servidores Dell R730xd E5-2650 v4 que cuestan 9,000 euros por un centavo?