El matemático aficionado descubrió la cobertura universal más pequeña

A través de cálculos geométricos difíciles, Philip Gibbs descubrió el recubrimiento más pequeño conocido para cualquier forma posible.

Una cubierta universal como un hexágono se puede describir alrededor de cualquier forma.

Philip Gibbs no es un matemático profesional. Por lo tanto, cuando quería reflexionar sobre una tarea, estaba buscando una que un aficionado pudiera manejar. Descubrió una tarea difícil que puede volver locas incluso a las mejores mentes. Y en un artículo publicado este año, Gibbs hizo un progreso significativo en la resolución de la cuestión de hace cien años, dependiendo de la capacidad de medir con precisión el área hasta escalas atómicas.

El primero en proponer este problema fue el matemático francés Henri Leon Lebesgue, en una carta a su amigo Julius Pal, escrita en 1914. Lebesgue preguntó: ¿cuál es la forma del área más pequeña posible, capaz de cubrir completamente una gran cantidad de otras formas (que tienen una propiedad común, que se describe a continuación)?

Durante el siglo pasado, la tarea de encontrar una cubierta universal se ha convertido en una trampa para ratones: el progreso para resolverlo, si sucedió periódicamente, siempre ha sido increíblemente pequeño. La mejora de Gibbs sobre esto se ha vuelto dramática, aunque todavía necesita pensar un poco al respecto.

Imagine una docena de recortes de papel de varios tamaños y formas en su piso. Ahora imagine que se le ofrece idear otra forma lo suficientemente grande como para cubrir cualquiera de las disponibles. A través de la experimentación, al superponer formas y darles la vuelta, puede encontrar alguna forma de resolver este problema. Pero, habiendo encontrado una cobertura universal, ¿puede estar seguro de haber encontrado la más pequeña? Puedes imaginar que durante el día vuelves periódicamente a tu forma y encuentras la oportunidad de cortar piezas adicionales aquí y allá.

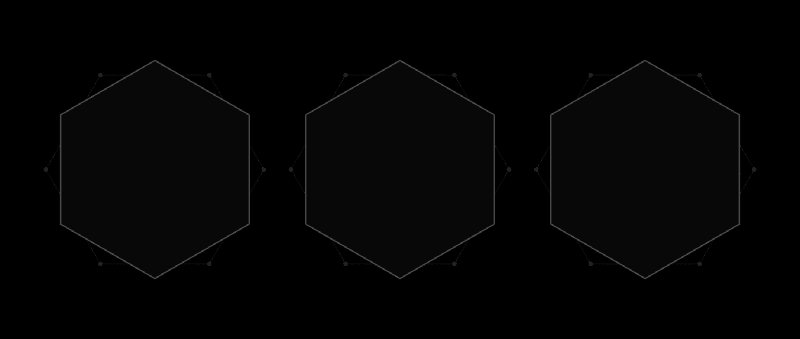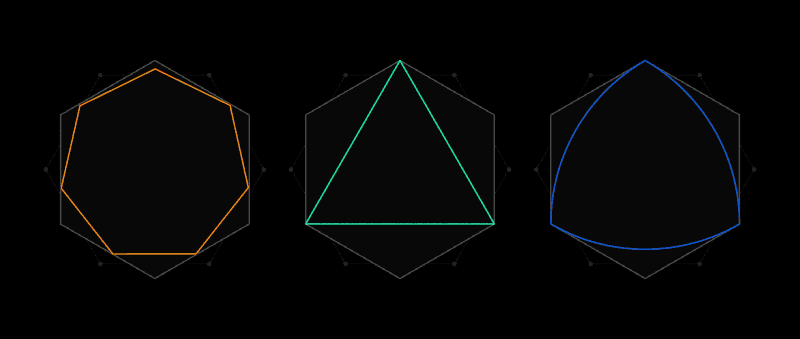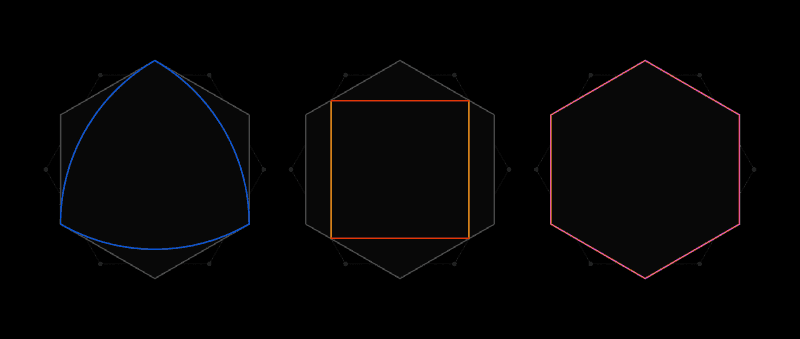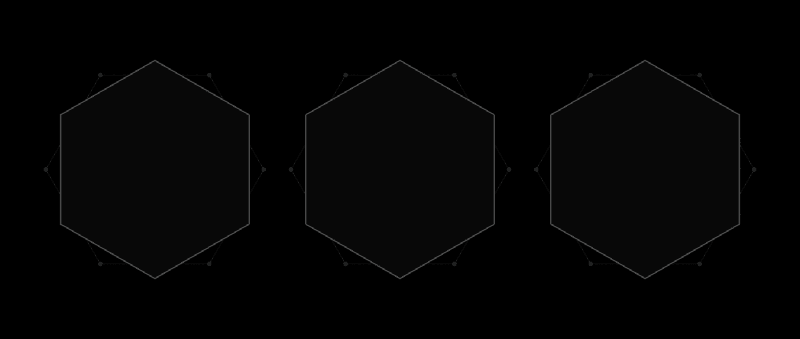
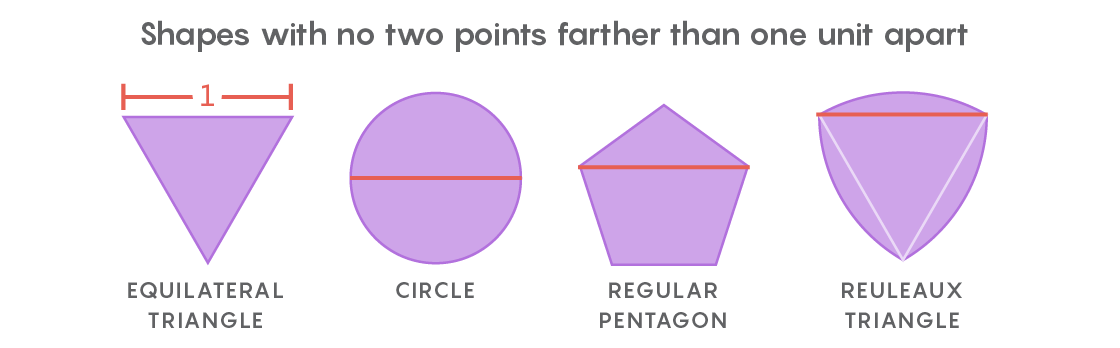
Este es el espíritu del problema de cobertura universal de Lebesgue. En lugar de recortes de papel, considera formas en las cuales dos puntos están separados no más allá de una unidad de longitud. La forma más obvia será un círculo de diámetro 1, pero hay un número infinito de ellos: un triángulo equilátero, un pentágono regular, un hexágono regular, una forma triangular con lados hinchados, conocido como el triángulo de Röhlo , y esto es solo para empezar. La variedad de formas hace que sea difícil encontrar la cubierta más pequeña para todas ellas.



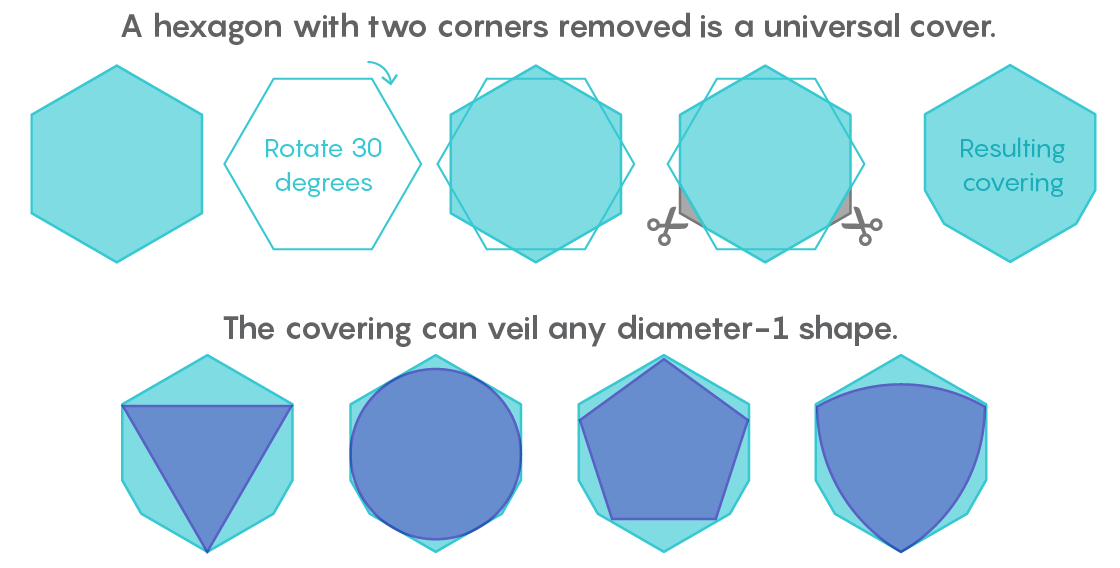
Poco después de recibir una carta de Lebesgue, Pal se dio cuenta de que el hexágono regular sería la cubierta universal. Y luego mejoró este resultado, señalando que cortando dos esquinas del hexágono, no de pie uno al lado del otro, puede obtener una forma con un área más pequeña, que seguirá siendo un recubrimiento universal.

“Tome un hexágono, coloque un segundo encima, gírelo 30 grados y corte dos esquinas. Ahí es donde Pal terminó la investigación ", dijo Gibbs.

En los siguientes 80 años, otros dos matemáticos cortaron tiras estrechas de la cubierta universal de Pal. En 1936, Roland Sprag retiró una pequeña pieza al lado de una de las esquinas. En 1992, Hansen eliminará dos cuñas en miniatura de las esquinas inferiores derecha e izquierda. Las ilustraciones de Hansen podrían transmitir la ubicación de estas partes, pero no su tamaño: su área era de 0.00000000004 unidades.



"No se pueden dibujar a escala, serían del tamaño de un átomo", dijo John Báez , matemático de la Universidad de California en Riverside.

Báez dejó de lado la tarea de Lebesgue cuando escribió sobre esto en su blog sobre matemáticas populares en 2013. Admitió que estaba fascinado por esta tarea de una manera que un video con un insecto ahogado podría fascinarte. "Mi interés en la tarea no era saludable", escribió Báez. "No sé las razones por las que podría ser importante". No veo cómo se puede conectar con muchas otras tareas maravillosas. Simplemente parece increíblemente complejo en comparación con la primera impresión. Admiro a las personas que trabajan en él tanto como admiro a las personas que deciden cruzar la Antártida con los esquís ".

Philip Gibbs nunca cruzó la Antártida en esquís, pero leyó el blog de Báez. Cuando se encontró con un registro del problema de Lebesgue, pensó: "Bueno, eso es exactamente lo que necesito".

Tijeras atómicas

Gibbs una vez pensó que podría convertirse en científico. Recibió un diploma en matemáticas de la Universidad de Cambridge y un doctorado en física teórica de la Universidad de Glasgow. Sin embargo, pronto perdió su entusiasmo por la investigación académica y se convirtió en programador. Trabajó en sistemas para diseño de barcos, gestión de tráfico aéreo y finanzas, y en 2006 se retiró.

Gibbs seguía interesado en los asuntos académicos, pero como investigador laico podía hacer poco. "Es difícil para un científico independiente hacer un seguimiento de lo que está sucediendo", dijo. "Pero si encuentra el nicho correcto, puede hacer algo y obtener algunos resultados útiles".


Matemático aficionado Philip Gibbs

Tal nicho era el problema de cobertura universal de Lebesgue. Esta tarea nunca recibió la atención de los matemáticos, por lo que sospechó que podría lograr algún progreso. Gibbs también se dio cuenta de que su experiencia en programación podría ser una ventaja. "Siempre busco problemas en los que se puedan usar las computadoras y las matemáticas experimentales", dijo.

En 2014, Gibbs ejecutó una simulación por computadora para 200 formas aleatorias de diámetro 1. De las simulaciones, se dedujo que podría cortar una pequeña pieza desde la esquina superior de la cubierta más pequeña anterior. Convirtió esto en una prueba de que el nuevo recubrimiento funcionará para todas las formas posibles de diámetro 1. Gibbs envió la prueba a Báez, quien, junto con una de sus estudiantes, Karina Baghdasaryan, ayudó a Gibbs a darle al trabajo un estilo matemático formal.

Los tres publicaron su trabajo en Internet en febrero de 2015. Redujo el área de la cobertura universal más pequeña posible de 0.8441377 a 0.8441153 unidades. El ahorro de 0.0000224 unidades fue casi un millón de veces mayor que lo que Hansen logró en 1992.

Gibbs confiaba en que podría mejorar el resultado. En un trabajo publicado en octubre, cortó otro trozo relativamente grande de un recubrimiento universal, llevando su área a 0.84409359 unidades.



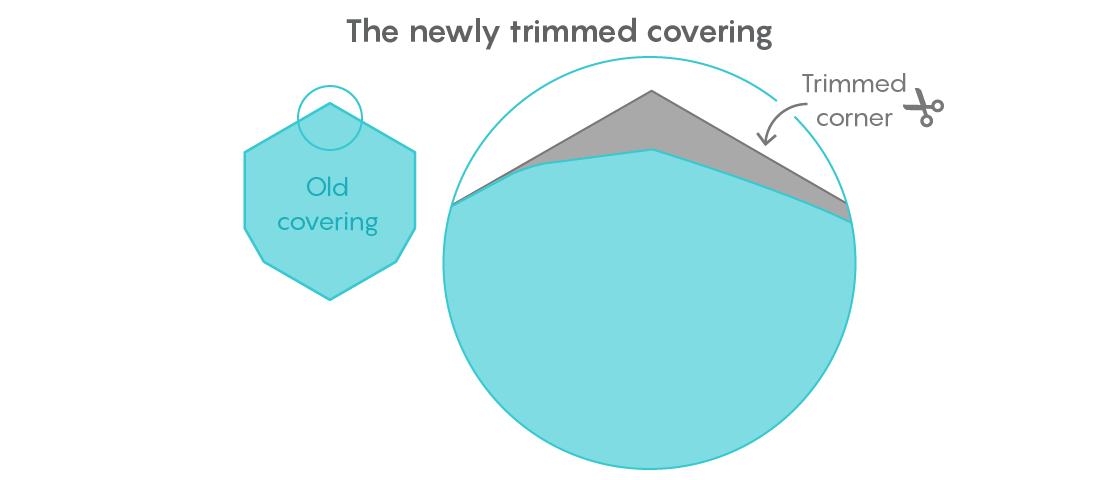
Su estrategia fue mover todas las formas con un diámetro de 1 a la esquina del revestimiento universal que descubrió hace varios años, y luego eliminar toda el área restante de la esquina opuesta. Pero una medición precisa del espacio ahorrado ha resultado difícil. Las técnicas utilizadas por Gibbs se basaron en la geometría euclidiana, pero se realizaron con tal precisión que sorprendería a cualquier estudiante de secundaria.

“Desde el punto de vista de las matemáticas, todo esto es geometría para la escuela secundaria. Pero actuó con una tensión fanática ” , escribió Báez.

Hasta ahora, Gibbs ocupa el primer lugar en busca de la cobertura universal más pequeña, pero su premio está en peligro. Gibbs cree que existe la oportunidad de encontrar una cobertura aún más pequeña. Báez espera que la atención que Gibbs volvió al problema de Lebesgue estimule el interés de otros matemáticos. Quizás es hora de dejar de lado la regla y la brújula y usar todo el arsenal de las matemáticas modernas.

"Es posible que la forma correcta de resolver este acertijo use ideas completamente diferentes", dijo, "aunque no tengo idea de qué ideas podría ser".