Profundidad de precisión claramente

La precisión de profundidad es una molestia que cualquier programador de gráficos enfrentará tarde o temprano. Se han escrito muchos artículos y trabajos sobre este tema. Y en diferentes juegos y motores, y en diferentes plataformas, puede ver muchos formatos y configuraciones diferentes para el búfer de profundidad .

La conversión de profundidad en una GPU parece obvia debido a cómo interactúa con la proyección en perspectiva, y el estudio de las ecuaciones no aclara la situación. Para entender cómo funciona esto, es útil dibujar algunas imágenes.



Este artículo está dividido en 3 partes:

1. Trataré de explicar la motivación para la transformación de profundidad no lineal .
2. Presentaré varios gráficos que lo ayudarán a comprender cómo funciona la conversión de profundidad no lineal en diferentes situaciones, de forma intuitiva y visual.
3. Una discusión de los principales hallazgos de Apretar la precisión del renderizado en perspectiva [Paul Upchurch, Mathieu Desbrun (2012)] con respecto al efecto de los errores de punto flotante redondeados en la precisión de la profundidad.

¿Por qué 1 / z?

Un búfer de profundidad de GPU de hardware generalmente no almacena una representación lineal de la distancia entre el objeto y la cámara, al contrario de lo que se espera ingenuamente de la primera reunión. En cambio, el búfer de profundidad almacena valores inversamente proporcionales a la profundidad del espacio de vista. Quiero describir brevemente la motivación para tal decisión.

En este artículo, usaré d para representar los valores almacenados en el búfer de profundidad (en el rango [0, 1] para DirectX), y z para representar el espacio de vista de profundidad, es decir. La distancia real de la cámara, en unidades mundiales, por ejemplo, metros. En general, la relación entre ellos tiene la siguiente forma:



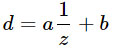
donde a, b son las constantes asociadas con la configuración cercana y lejana de los planos. En otras palabras, d es siempre una transformación lineal de 1 / z .

A primera vista, puede parecer que cualquier función de z puede tomarse como d . Entonces, ¿por qué se ve así? Hay dos razones principales para esto.

En primer lugar, 1 / z encaja naturalmente en la proyección en perspectiva. Y esta es la clase más básica de transformaciones, que garantiza preservar las líneas rectas. Por lo tanto, la proyección en perspectiva es adecuada para la rasterización de hardware, ya que los bordes rectos de los triángulos permanecen rectos en la pantalla. Podemos obtener una transformación lineal de 1 / z , aprovechando la división de perspectiva que la GPU ya realiza:



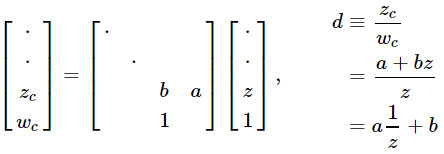
Por supuesto, la verdadera fortaleza de este enfoque es que la matriz de proyección se puede multiplicar con otras matrices, lo que le permite combinar muchas transformaciones en una sola.

La segunda razón es que 1 / z es lineal en el espacio de la pantalla, como señaló Emil Persson . Esto hace que sea fácil interpolar d en el triángulo durante la rasterización, y cosas como los amortiguadores Z jerárquicos , el sacrificio Z temprano y el búfer de profundidad de compresión .

Gráficos de profundidad

Las ecuaciones son complicadas, ¡veamos un par de imágenes!



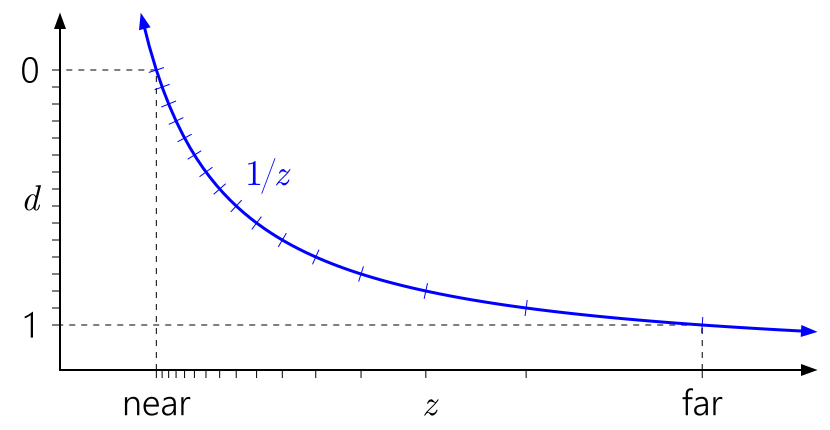
La forma de leer estos cuadros es de izquierda a derecha, luego hacia abajo. Comience con d en el eje izquierdo. Dado que d puede ser una transformación lineal arbitraria de 1 / z , podemos organizar 0 y 1 en cualquier lugar conveniente del eje. Las marcas indican diferentes valores de tampón de profundidad . Para fines de claridad, modelé un búfer de profundidad normalizado de enteros de 4 bits, por lo que hay 16 marcas espaciadas uniformemente.

El gráfico anterior muestra la conversión de profundidad de vainilla "estándar" a D3D y API similares. Puede notar de inmediato cómo, debido a la curva 1 / z , se agrupan los valores cercanos al plano cercano y se dispersan los valores cercanos al plano lejano.

También es fácil entender por qué cerca de un plano afecta tanto la precisión de profundidad. La distancia cerca del plano conducirá a un rápido aumento en los valores de d en relación con los valores de z , lo que conducirá a una distribución de valores aún más desigual:



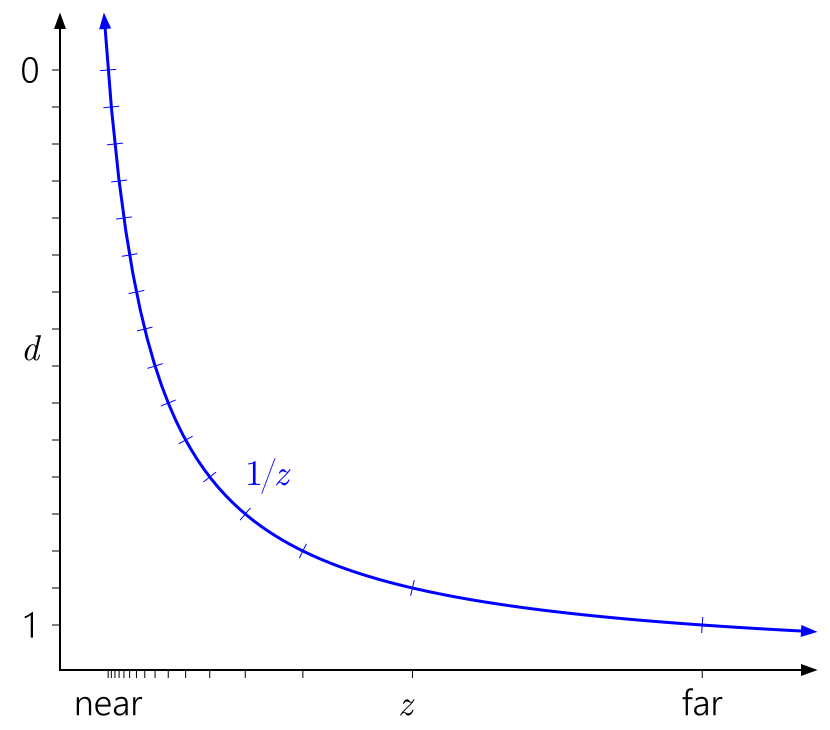
Del mismo modo, en este contexto, es fácil ver por qué mover el plano lejano al infinito no tiene un efecto tan grande. Simplemente significa expandir el rango de d a 1 / z = 0 :



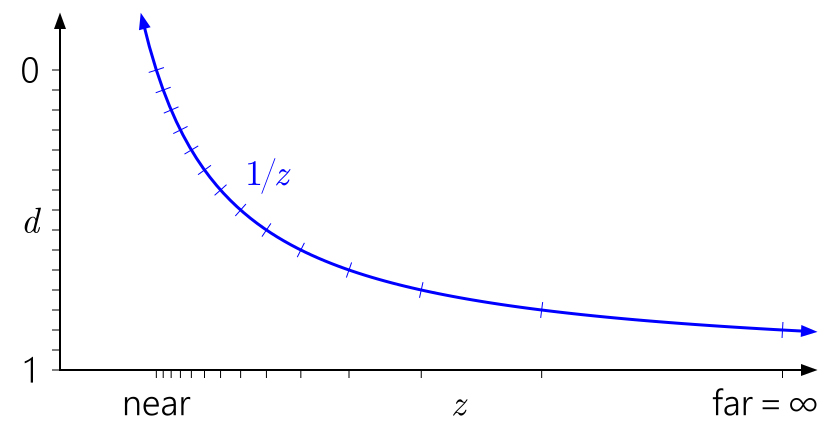
Pero, ¿qué pasa con la profundidad de punto flotante? Al siguiente gráfico se le han agregado marcas correspondientes al formato flotante con 3 bits del exponente y 3 bits de la mantisa:



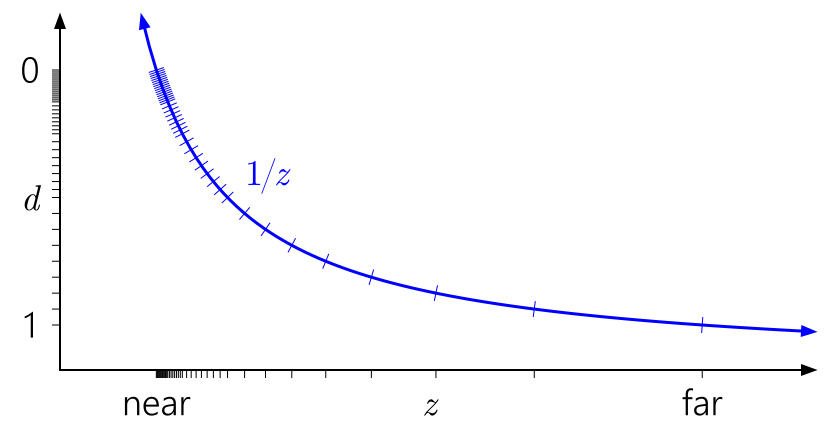
Ahora en el rango [0,1] hay 40 valores diferentes, un poco más de 16 valores anteriores, pero la mayoría de ellos están agrupados inútilmente cerca del plano cercano (más cerca de 0 el flotador tiene mayor precisión), donde realmente no necesitamos mucha precisión.

Ahora, un truco bien conocido es invertir la profundidad, mostrando el plano cercano en d = 1 y el plano lejano en d = 0 :



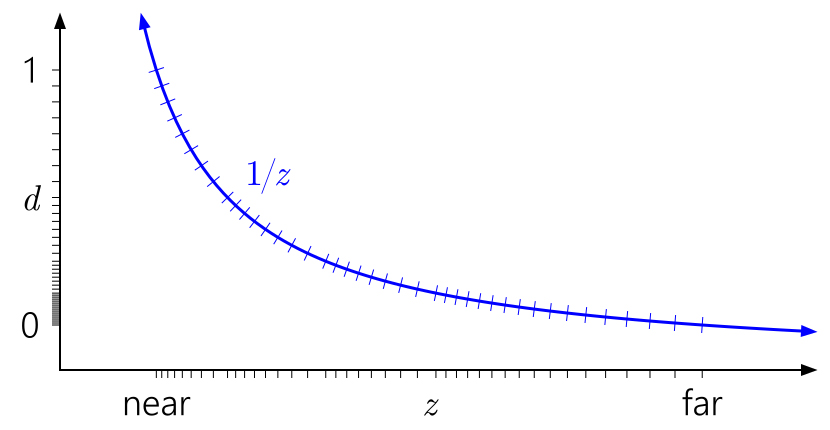
Mucho mejor! Ahora, la distribución cuasi-logarítmica de flotación compensa de alguna manera la no linealidad de 1 / z , mientras que más cerca del plano cercano proporciona una precisión similar al búfer de profundidad de enteros, y proporciona una precisión significativamente mayor en otros lugares. La precisión de profundidad se deteriora muy lentamente si te alejas de la cámara.

El truco Z invertido puede haberse reinventado de forma independiente varias veces, pero al menos la primera mención fue en el artículo SIGGRAPH '99 [Eugene Lapidous y Guofang Jiao (desafortunadamente no está disponible públicamente)]. Y recientemente, Matt Petineo y Brano Kemen lo volvieron a mencionar en el blog, y en un discurso de Emil Persson Creando Vast Game Worlds SIGGRAPH 2012.

Todos los gráficos previos asumieron un rango de profundidad [0.1] después de la proyección, lo cual es una convención en D3D. ¿Qué hay de OpenGL ?



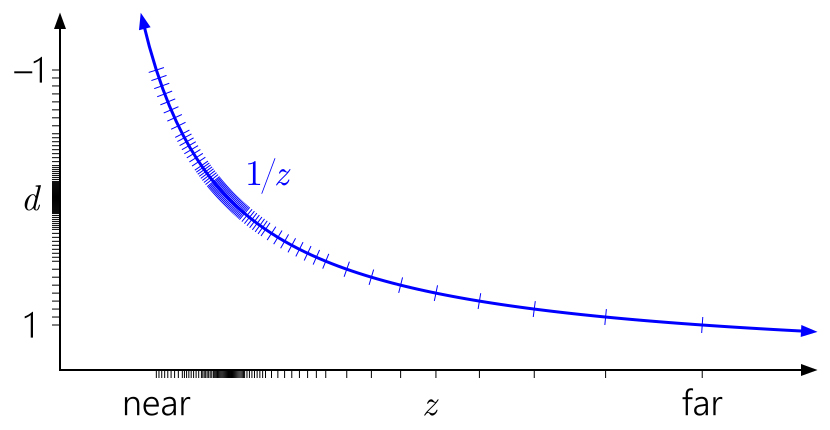OpenGL por defecto asume un rango de profundidad [-1, 1] después de la proyección. Para formatos enteros, nada cambia, pero para punto flotante toda la precisión se concentra inútil en el medio. (El valor de profundidad se asigna al rango [0,1] para su posterior almacenamiento en el búfer de profundidad, pero esto no ayuda, ya que la asignación inicial a [-1,1] ya destruyó toda la precisión en la mitad lejana del rango). Y debido a la simetría, el truco Z invertida no funcionará aquí.

Afortunadamente, en el escritorio OpenGL, esto se puede solucionar utilizando la extensión ARB_clip_control ampliamente compatible (también comenzando con OpenGL 4.5, glClipControl es estándar ). Desafortunadamente, GL ES está en vuelo.

El efecto de los errores de redondeo

La conversión 1 / z y la elección del búfer de profundidad flotante vs int es una gran parte de la historia de precisión, pero no todo. Incluso si tiene suficiente precisión de profundidad para representar la escena que está tratando de representar, es fácil degradar la precisión con errores aritméticos durante el proceso de conversión de vértices.

Al comienzo del artículo, se mencionó que Upchurch y Desbrun estudiaron este problema. Propusieron dos recomendaciones principales para minimizar los errores de redondeo:

1. Usa infinito plano lejano.
2. Mantenga la matriz de proyección separada de otras matrices y aplíquela como una operación separada en el sombreador de vértices, en lugar de combinarla con la matriz de vista.

Upchurch y Desbrun hicieron estas recomendaciones utilizando un método analítico basado en el procesamiento de errores de redondeo como pequeños errores aleatorios presentados en cada operación aritmética y rastreándolos hasta el primer orden en el proceso de conversión. Decidí probar los resultados en la práctica.

Las fuentes aquí son Python 3.4 y numpy. El programa funciona de la siguiente manera: se genera una secuencia de puntos aleatorios, ordenados por profundidad, ubicados linealmente o logarítmicamente entre planos cercanos y lejanos. Luego, los puntos se multiplican por la vista y la proyección de la matriz y se realiza la división en perspectiva, utilizando flotantes de 32 bits, y opcionalmente el resultado final se convierte en un int de 24 bits. Al final, pasa a través de la secuencia y cuenta cuántas veces 2 puntos vecinos (que inicialmente tenían profundidades diferentes) se volvieron idénticos, porque tenían la misma profundidad o el orden cambió en absoluto. En otras palabras, el programa mide la frecuencia con la que ocurren los errores de comparación de profundidad, que corresponde a problemas como la lucha Z , en varios escenarios.

Aquí están los resultados para cerca = 0.1, lejos = 10K, con una profundidad lineal de 10K. (Probé el intervalo de profundidad logarítmica y otras proporciones cercanas / lejanas, y aunque los números específicos variaron, las tendencias generales en los resultados fueron las mismas).

En la tabla, "eq" - dos puntos con la profundidad más cercana obtienen el mismo valor en el búfer de profundidad, y "swap" - se intercambian dos puntos con la profundidad más cercana.

	Matriz de vista-proyección compuesta		Vista separada y matrices de proyección
	float32	int24	float32	int24
Valores Z sin cambios (prueba de control)	0% eq 0% de intercambio	0% eq 0% de intercambio	0% eq 0% de intercambio	0% eq 0% de intercambio
Proyección estándar	45% eq 18% de intercambio	45% eq 18% de intercambio	77% eq 0% de intercambio	77% eq 0% de intercambio
Infinito lejos	45% eq 18% de intercambio	45% eq 18% de intercambio	76% eq 0% de intercambio	76% eq 0% de intercambio
Z invertido	0% eq 0% de intercambio	76% eq 0% de intercambio	0% eq 0% de intercambio	76% eq 0% de intercambio
Infinito + Z invertido	0% eq 0% de intercambio	76% eq 0% de intercambio	0% eq 0% de intercambio	76% eq 0% de intercambio
Estándar + estilo GL	56% eq 12% de intercambio	56% eq 12% de intercambio	77% eq 0% de intercambio	77% eq 0% de intercambio
Infinito + estilo GL	59% eq 10% de intercambio	59% eq 10% de intercambio	77% eq 0% de intercambio	77% eq 0% de intercambio

Pido disculpas por el hecho de que sin un gráfico, ¡hay demasiada dimensión aquí y simplemente no puedo construirlo! En cualquier caso, mirando los números, las siguientes conclusiones son obvias:

• En la mayoría de los casos, no hay diferencia entre el búfer de profundidad int y flotante . Errores aritméticos para calcular errores de anulación de profundidad en la conversión a int. En parte porque float32 e int24 tienen una ULP casi igual (la unidad de menor precisión es la distancia al número vecino más cercano) en [0.5.1] (dado que float32 tiene una mantisa de 23 bits), por lo que no se agrega un error de conversión en casi todo el rango de profundidad en int.
• En la mayoría de los casos, la separación de las matrices de vista y proyección (siguiendo las recomendaciones de Upchurch y Desbrun) mejora el resultado. A pesar de que la tasa de error general no disminuye, los "intercambios" se convierten en valores iguales, y este es un paso en la dirección correcta.
• El plano lejano infinito cambia ligeramente la frecuencia de los errores. Upchurch y Desbrun predijeron una reducción del 25% en la frecuencia de errores numéricos (errores de precisión), pero esto no parece conducir a una disminución en la tasa de error de comparación.

Sin embargo, los hallazgos anteriores no son reales en comparación con la magia Z invertida . Comprobar:

• La Z invertida con búfer de profundidad flotante proporciona una tasa de error cero en la prueba. Ahora, por supuesto, puede obtener algunos errores si continúa aumentando el intervalo de valores de profundidad de entrada. Sin embargo, la Z invertida con flotación es ridículamente más precisa que cualquier otra opción.
• Reversed-Z con buffer de profundidad de enteros es tan bueno como otras opciones de enteros.
• La Z invertida difumina la distinción entre matrices de vista / proyección compuestas y separadas, y planos lejanos finitos e infinitos. En otras palabras, con Z invertida puede multiplicar la proyección con otras matrices y usar cualquier plano lejano que desee, sin comprometer la precisión.

Conclusión

Creo que la conclusión es clara. En cualquier situación, cuando se trata de la proyección en perspectiva, solo use el búfer de profundidad de flotación y la Z invertida . Y si no puede usar el búfer de profundidad de flotación, aún debe usar Z invertida. Esto no es una panacea para todos los males, especialmente si crea un entorno de mundo abierto con rangos de profundidad extrema. Pero este es un gran comienzo.