
Hola Habr! Mi nombre es Akhmadeev Rinat, soy el Sr. Desarrollador PHP.
Te presento el resumen del informe. ¡ Haz que las contraseñas vuelvan a ser geniales! Cómo derrotar a la fuerza bruta y dejar a los hackers sin nada de Alexey Ermishkin de Virgil Security con HighLoad ++ 2018 .
Cuando fui al informe, era pesimista. Pero desde Como se trata de Virgil Security, aún así decidí ir. Al principio, el informe parecía realmente del capitán, e incluso comencé a perder interés, pero luego, como resultó, incluso descubrí varios enfoques nuevos para la protección con contraseña, además del hash de sal habitual.
El informe analiza formas de proteger las contraseñas de los hash a enfoques más modernos, como la contraseña de Facebook, Onion, Sphinx y Pythia. Al final, se presenta el nuevo Servicio simple de cifrado reforzado con contraseña (PHE).
Me gustó tanto el informe que preparé un compendio. Recomiendo a todos que se familiaricen.
Alexey Ermishkin compartió las diapositivas y el informe de video en los comentarios:
Resumen
Entrada

Hola a todos, buenos días a todos! Me alegro de verlos a todos en la Conferencia de Highload. Mi nombre es Alexey Ermishkin, trabajo para Virgil Security.

Nos dedicamos al desarrollo de varios productos criptográficos tanto para desarrolladores individuales como para empresas. Nos centramos en soluciones integrales, esto es cuando no necesita confiar en el servicio para realizar acciones como la transferencia de datos, la autenticación, etc. Nuestros SDK son abiertos y accesibles para todos.
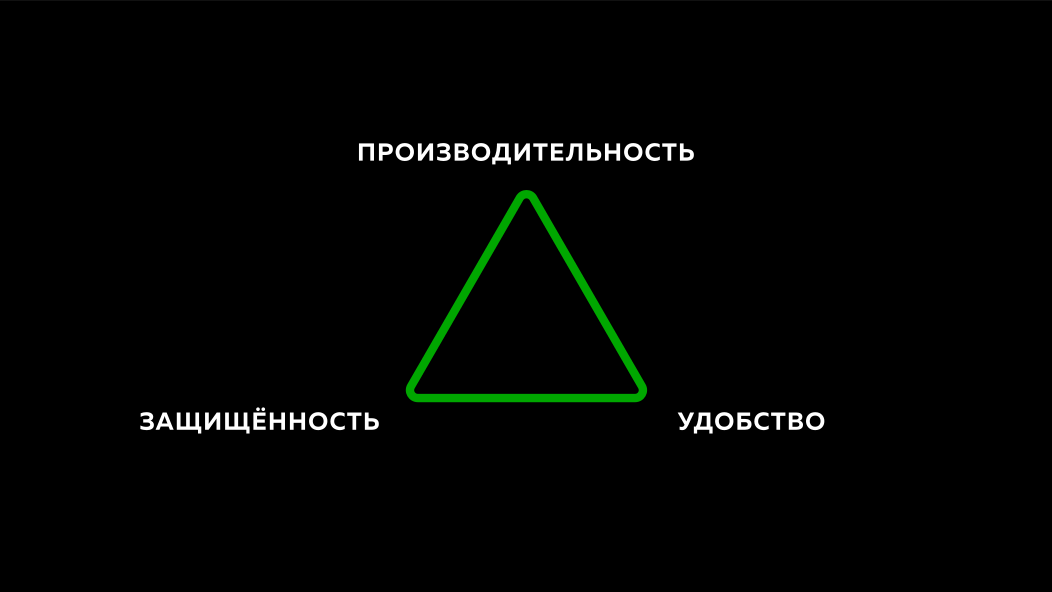
Las contraseñas se han utilizado durante mucho tiempo como un medio de autenticación, como una forma de llegar a algún lado. Eso fue mucho antes de que aparecieran las computadoras. Pero con la llegada de las computadoras, con la llegada de los sistemas de TI, las personas no han abandonado el hábito de usar contraseñas. Esto se convirtió en un gran problema para los desarrolladores, porque se encontraron con el problema de cómo hacer que los sistemas sean convenientes, rápidos y seguros. Muy a menudo, cuando dos de estos aspectos intentan hacerlo bien, el tercero no funciona muy bien. Si hace que el sistema sea productivo y seguro, puede ser inconveniente, etc.

Entonces, ¿de qué vamos a hablar hoy?
Hablaré sobre la protección contra ataques fuera de línea. Cuando las contraseñas ingresan a sus bases de datos, el usuario no las controla. Si su base de datos está pirateada, se filtra en alguna parte, luego los hackers pueden hacer cualquier cosa con ella. Incluso si de alguna manera protegió las contraseñas, pueden comenzar a resolverlas y para esto no necesitan interactuar con nadie, ya tienen todo para esto. Además, los usuarios no dejan de usar contraseñas débiles. Las políticas de contraseña son, por supuesto, algo útil, pero no siempre convenientes, es decir cuando incluso las personas ingresan, parece una contraseña segura, la política aún dice que necesita agregar una letra o número, entonces para ellos no es conveniente. También es obvio que el problema es la necesidad de comparar lo que el usuario ingresó con lo que tiene en la base de datos. ¿Cómo hacerlo de forma segura? Bueno, no olvidemos que dentro de la empresa también hay personas que no son completamente amigables y que también desean protegerse de ellos.
Hashes
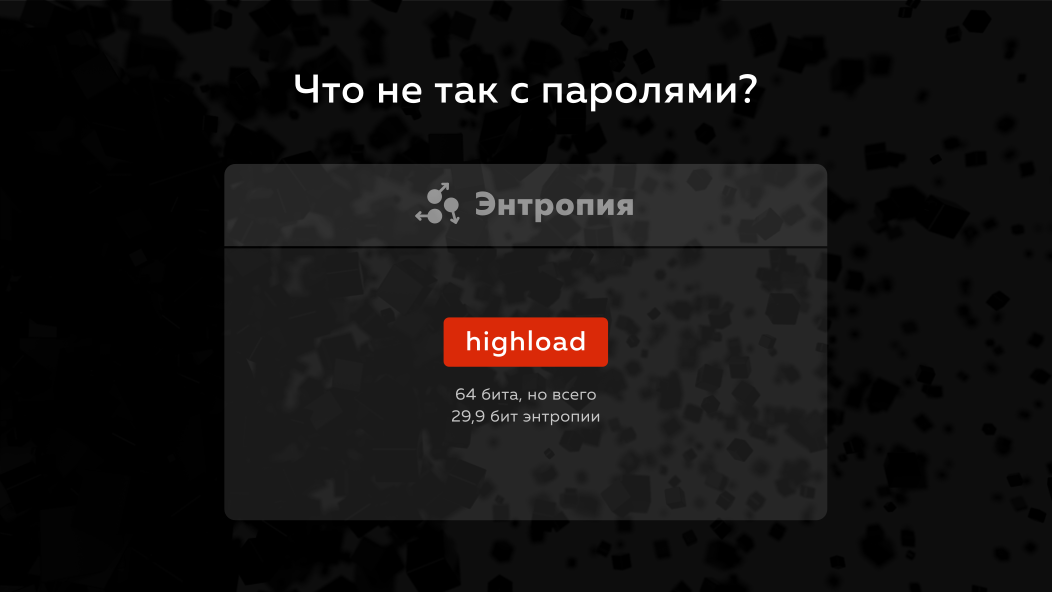
En principio, ¿por qué las contraseñas son un tema tan doloroso? ¿Por qué vale la pena trabajar con ellas con más cuidado? El problema es que la contraseña tiene una pequeña entropía . ¿Qué es la entropía? Esta es la cantidad de información contenida en los datos, es decir por ejemplo, en la palabra Highload, 8 letras son 8 bytes, pero si contamos la entropía, no serán 64 bits como la palabra completa, sino menos de 30 bits. Cuando hoy hablan de romper una contraseña, dicen que es posible descifrar contraseñas con entropía en un momento en el que no haya más ni menos bits. Es decir ni siquiera se tiene en cuenta la cantidad de contraseñas.

¿Cómo comenzó la gente con la seguridad de contraseña? Lo primero que se me ocurrió fue usar hashes criptográficos unidireccionales.

Su característica notable es que no se pueden volver atrás. Es decir Si transfirió alguna información a este hash, recibió un valor en la salida, no puede recuperar esta información de este valor. Pero, desafortunadamente, se calculan muy rápidamente. Por ejemplo, un grupo moderno de 4 tarjetas gráficas NVidia puede procesar varios miles de millones de contraseñas por segundo. Es decir Si la entropía de su contraseña es inferior a 40 bits, entonces un grupo de 4 tarjetas de video la recogerá en un minuto, o incluso menos.
Mesas arcoiris

Además, cada hash complicado tiene su propia tabla de arcoiris . ¿Qué es esta mesa y cómo se hacen?

Es decir toman las contraseñas y combinaciones de caracteres más populares que pueden caber en el disco duro, consideran los hashes y las almacenan un poco más para varios terabytes. Cuando hay algún tipo de hash, no puede calcularlo, pero encuéntrelo muy rápido en estas tablas y compárelo con la contraseña que se calculó previamente. Es decir Las ventajas de las tablas son que funcionan muy rápidamente, pero necesita mucho espacio para almacenarlas. Sin embargo, hay tablas para los hashes más populares en Internet, se pueden descargar o incluso comprar.
Nota del autor de la sinopsis: Wikipedia no está de acuerdo con el orador: "La tabla del arco iris es una versión especial de las tablas de búsqueda para revertir las funciones hash criptográficas utilizando el mecanismo de un compromiso razonable entre el tiempo de búsqueda en la tabla y la memoria ocupada". Es decir no almacena los valores hash de las contraseñas más populares que caben en el disco, sino simplemente los valores hash de algunas contraseñas, el resto se calcula sobre la base de las que existen: hay varias contraseñas por registro en la tabla.
Sal

Pero, de nuevo, cada mesa arcoiris tiene su propia sal . ¿Qué es la sal? Este es un conjunto aleatorio de bytes, que se agrega a la contraseña. Se almacena en una tabla en algún lugar cerca del hash y protege de las tablas del arco iris.

Es decir las personas que tengan en sus manos una base con hash salados aún tendrán que calcular estos hash. Pero el problema es que estos hashes se calculan muy rápidamente y la sal no ayuda mucho aquí.
¿Cómo ralentizar la búsqueda?

Una forma natural de salir de esto podría ser ralentizar la clasificación de hash de alguna manera. ¿Cómo se puede hacer esto?

El enfoque más ingenuo es que tomamos algún tipo de función hash, por ejemplo sha256, y la calculamos iterativamente, es decir calcule el hash, a partir de este hash el hash nuevamente, etc. Puedes hacer esto muchos miles e incluso millones de veces. El problema es que si escribe dicha implementación usted mismo, lo más probable es que sea más lenta que la implementación de personas involucradas profesionalmente en la adivinación de contraseñas.

SCrypt , Bcrypt , Argon2
Y, por lo tanto, a los criptógrafos se les ocurrieron varias funciones que están específicamente diseñadas para ralentizar la búsqueda de contraseñas: utilizan una gran cantidad de memoria y todas las instrucciones modernas posibles del procesador. Si la contraseña protegida por dicha función cae en manos de los atacantes, tendrán que usar hardware muy potente.

Por ejemplo, la función Argon2 más moderna funciona de la siguiente manera: en el diagrama puede ver que hay muchos bloques de memoria diferentes a través de los cuales se ejecuta el hash. Lo hace de varias maneras, ida y vuelta, la memoria se usa muy intensamente, se usa toda la memoria. Es bastante difícil optimizar dicha función (velocidad de búsqueda).

Pero estos enfoques también tienen sus inconvenientes. Estas funciones se hacen especialmente lentas, pero son especialmente lentas no solo para los atacantes, sino que también serán especialmente lentas para ti. Cargarán tu plancha. Estas funciones son personalizables, es decir puede elegir cuánta memoria se usará para calcular el hash de una sola contraseña, hasta varios gigabytes, cuántas pasadas en esta memoria. Si enrolla estos parámetros muy en serio, su propio hardware se verá afectado y si hay muchas personas que inician sesión en el sistema, entonces solo tiene que asignar recursos bastante importantes para la protección de contraseñas y contraseñas simples, bueno, aún se pueden obtener contraseñas muy simples .
Cebolla de la contraseña de Facebook

La gente pensó en esto y formuló la pregunta: ¿es posible lograr las mismas propiedades sin cargar el backend, sin cargar sus propios servidores?

Uno de los pioneros en esto fue Facebook . Estas líneas que ves son las etapas históricas de Facebook, cómo protegieron las contraseñas, al principio solo eran contraseñas, luego tomaron la antigua función md5 , que estuvo agrietada durante mucho tiempo, luego agregaron sal y tomaron el hash sha1 , y luego sucedió Lo interesante, trajeron el cálculo de la función hmac (esto es un hash con una clave) al servicio remoto.
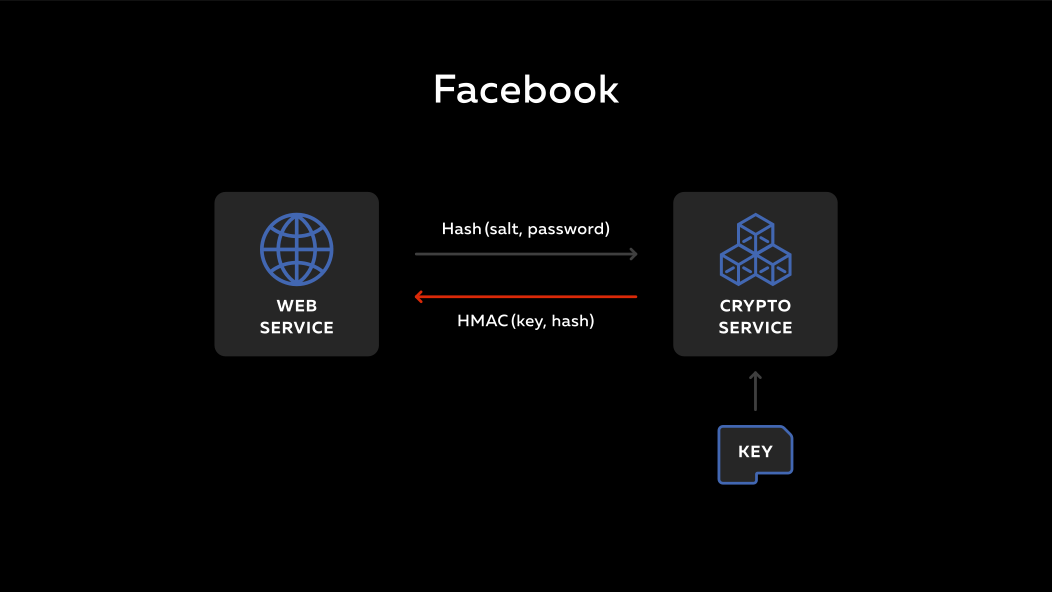
Como funciona Hay un backend, hay un servicio remoto. Hay algún tipo de clave secreta en este servicio. Una persona ingresa al backend, ingresa su contraseña. Esta contraseña se mezcla con la sal que está en la base de datos, se ejecuta a través de un hash y se envía al servicio. El servicio toma su clave privada, calcula la función hmac y la envía de vuelta. En el backend, se coloca en la base.
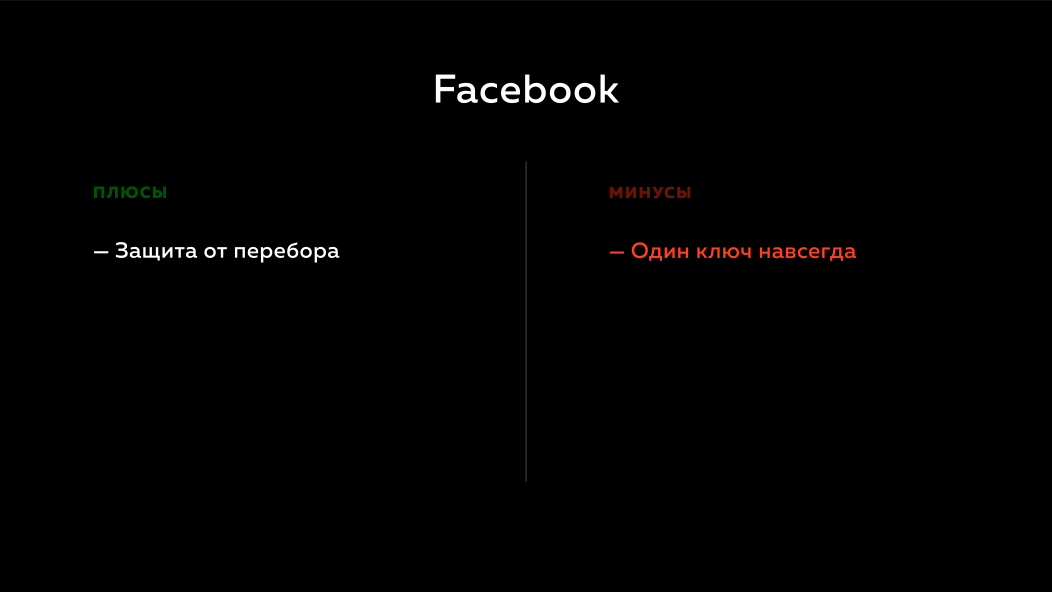
Que da Si Facebook tiene una base de datos de usuarios, entonces no vale la pena ordenar las contraseñas porque no tienen una clave secreta remota. Pero el problema con el enfoque de Facebook es que si algo le sucede a su clave privada remota, estarán en un gran problema. No pueden hacer nada al respecto porque usan hashes, usan hmac. No tienen forma de resolver de alguna manera esta situación para que los usuarios no noten nada y esto se arrinconará.
Esfinge
Los criptógrafos lo miraron todo. Les gustó la idea de usar servicios remotos y decidieron pensar: ¿es posible hacerlo aún mejor? ¿Es posible hacer un sistema similar, pero sin las desventajas que Facebook le ha dotado?

Y decidieron abordar este problema de la siguiente manera: ¿qué sucede si la contraseña o el hash de contraseña se representan como un número? Si tenemos la palabra passw0rd , consta de 8 bytes. En casi todos los lenguajes de programación, hay tipos enteros de ocho bytes, es decir, En principio, este es uno y el mismo. Es decir 8 bytes, la palabra passw0rd y podemos representarlo como un número decimal regular. ¿Qué nos da esto? Esto nos da una libertad de acción completamente diferente. Podemos agregar contraseñas o hashes de ellos, multiplicarlos, convertirlos en otros números. Podemos realizar operaciones matemáticas realmente serias con ellos.

Uno de los primeros sistemas que utilizó esta tecnología fue Sphinx . Ella apareció hace un par de años. Este es un administrador de contraseñas determinista. Hay muchos programas diferentes, como keepass , donde tiene una contraseña maestra y para cada sitio genera una contraseña aleatoria. Pero también hay cosas deterministas en las que ingresa su contraseña maestra, el sitio al que desea ir y calcula algo allí y emite una contraseña única para cada sitio. Pero está claro que si esta contraseña maestra va a algún lado, todas las contraseñas de sus sitios se verán comprometidas permanentemente.
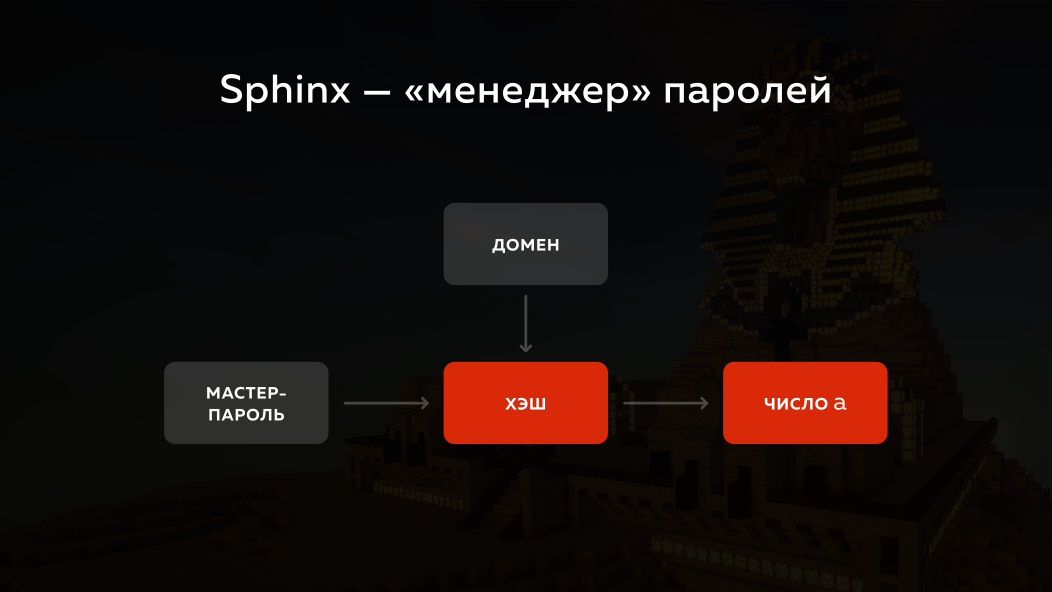
¿Cómo enfrentó Sphinx este problema? Toma la contraseña maestra, toma el dominio en el que desea iniciar sesión, ejecuta todo a través de un hash y lo convierte en un número. Pero, de hecho, la criptografía elíptica se usa allí, por simplicidad explicaré todo esto en números ordinarios con matemáticas ordinarias. Lo convierte en un número (llamémoslo a ) y ¿qué hace después?

Absolutamente maravilloso, cada vez que podemos generar un gran número aleatorio r . Si elevamos el número a a la potencia de r , y en algún momento más tarde elevamos este número a la potencia inversa al número r , entonces recuperamos el mismo número a , ¿verdad? Es decir podemos enmascarar algo desde el principio y luego desenmascararlo.
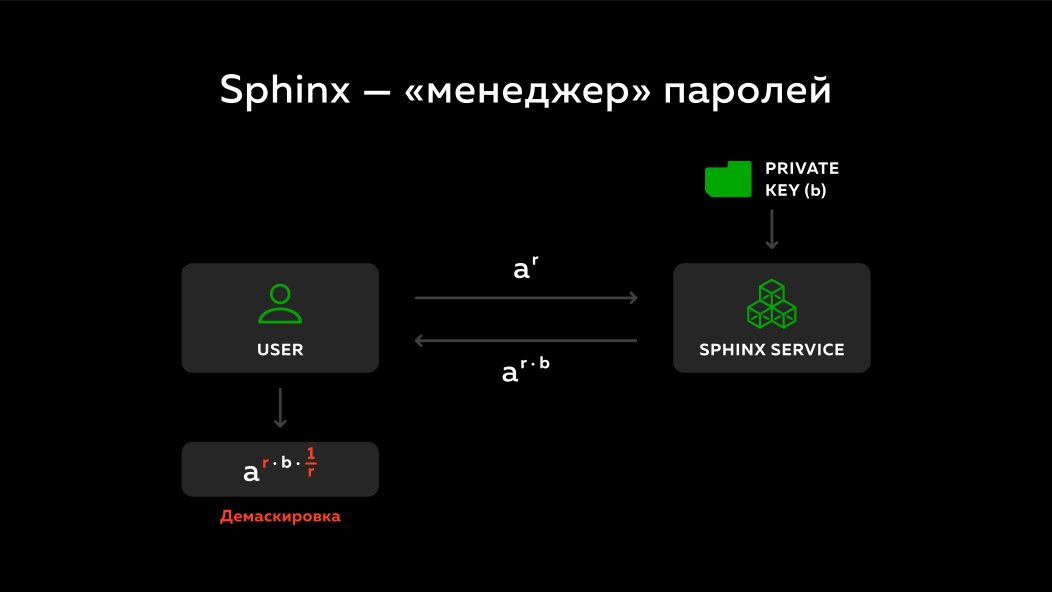
¿Y qué hace la esfinge? Nuevamente hay un usuario, hay un servicio remoto. Se envía un número enmascarado a este servicio remoto. En el servicio remoto, hay una clave privada b . Que esta haciendo el Multiplica el número enviado a^r por su clave secreta b y lo devuelve. ( Nota del autor del compendio: en la diapositiva, el número enviado no se multiplica por la clave privada, sino que se eleva al grado de la clave privada, pero el punto principal sí ). Como el número r diferente cada vez, el servicio remoto no puede decir nada sobre qué contraseña y dominio se enmascararon, es decir, cada vez que ve algunos números aleatorios diferentes. Y simplemente se multiplica por su clave privada b y envía de vuelta.
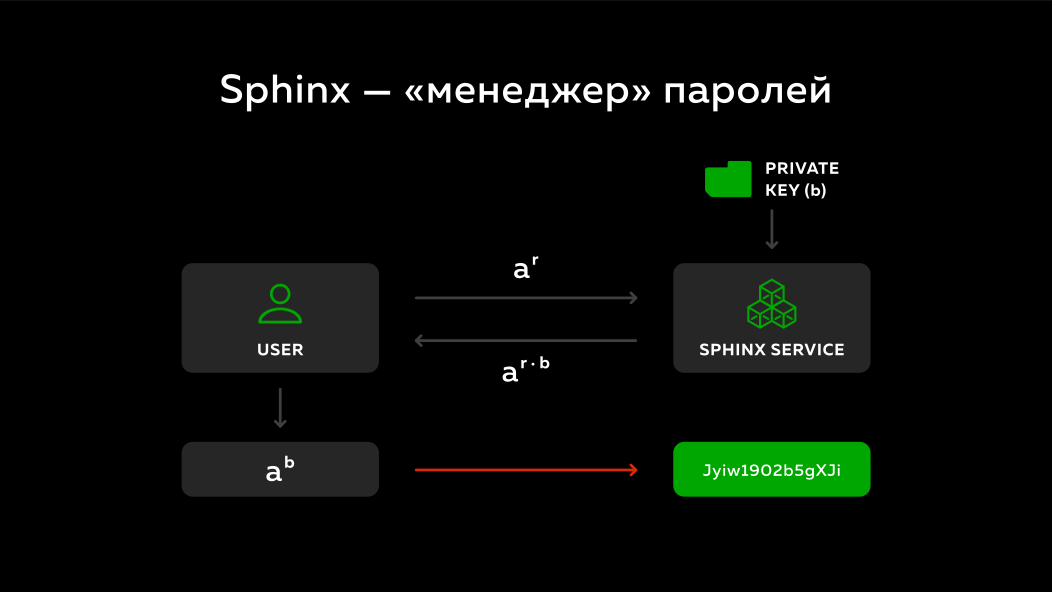
El usuario desenmascara lo que el servidor le envió y obtiene un número: su contraseña maestra con el dominio multiplicado por la clave secreta del servidor a^b . Resulta que no conoce la clave secreta del servidor, el servidor no sabe lo que el usuario le envió, pero al final también obtiene algún tipo de número determinista. Cada vez que ejecute este protocolo, el disfraz será diferente, pero el resultado siempre será el mismo y este resultado se puede volver a convertir en algún tipo de contraseña y utilizar para ingresar a varios sitios.

Realmente maravillosa tecnología. Primero, puede generar contraseñas grandes, es decir Protege de la ruptura. En segundo lugar, si un hacker obtiene acceso a varias contraseñas, no podrá decir nada sobre el resto, porque se generan independientemente uno del otro. En tercer lugar, si la contraseña del usuario desaparece en algún lugar, esto tampoco dará nada, porque los piratas informáticos no tendrán una clave secreta. Cuarto, funciona muy rápido porque no se necesitan hashes grandes iterativos aquí, es decir literalmente se realizan 2-3 multiplicaciones y todo funciona al instante.
Pero este sistema tiene sus inconvenientes. El servidor con el que está hablando el usuario no sabe nada de él. Simplemente recibe algunos números aleatorios como entrada, los multiplica por algo y los envía de vuelta. El cliente tampoco sabe nada sobre el servidor, envía algo a alguna parte, recibe el resultado, funciona, bueno. Pero si algo le sucede al servicio, el usuario no podrá decir nada al respecto, no tiene información para esto. La clave secreta tampoco se puede cambiar; no se puede hacer nada con ella.
Pitia

¿Podría ser mejor?

Los criptógrafos observaron este sistema y pensaron: ¿es posible mejorar el sistema y complementarlo con propiedades que nos permitan decir que cumple con los principios de extremo a extremo? Es decir el cliente puede comunicarse con el servidor, pero al mismo tiempo, también puede autenticarlo y confiar en él hasta cierto punto.

Y se les ocurrió un protocolo llamado Pythia .

Fue hecho por el maravilloso hombre Adam Everspaugh con sus colegas. ¿Qué lo hace único? En primer lugar, el servicio sabe quién ingresa la contraseña, es decir el ID de usuario se pasa al servidor más allá de la contraseña. Puede ser un cuadro de identificación aleatorio que se encuentra al lado, o simplemente un nombre de usuario. No importa Pero el servicio lo sabe. Pero el servidor no solo sabe un poco de esto, sino que puede probar matemáticamente estrictamente que es él.

Como funciona Hay un backend (algún tipo de servicio web, sitio) y hay un servicio Pythia. ¿Qué hace el backend y qué hace el servicio? Hay una clave privada k en el servicio, pero también transfiere su clave pública al backend. El backend del servicio envía no solo el número enmascarado a^r , como en el protocolo Sphinx, sino que también envía algún tipo de identificador de usuario ( UserID ). El servicio multiplica el ID de usuario y la contraseña por su clave privada y el resultado (UserID, a)^(r*k) ID de usuario (UserID, a)^(r*k) envía el backend. También envía una cierta Proof , que puede ser utilizada por el backend para verificar que el servidor no ha sido pirateado, que está respondiendo como debería.

Luego hay un desenmascaramiento y el número y que resulta como resultado se coloca en un DB. En la base de datos no solo tenemos un hash, sino un número, un punto de una curva elíptica.

Aquí hay algunos puntos interesantes:
- La capacidad del servidor para combinar el ID de usuario y la contraseña en un solo número. Esto se llama operación bilineal o emparejamiento bilineal. Esta es una matemática relativamente nueva, que recientemente comenzó a usarse. Ella tiene todas las propiedades de los nuevos matemáticos en que no han pasado 30 años para que todos estén convencidos de que todo es normal con esto.
- Pero la
Proof que envía el servicio es una tecnología bastante antigua. Esto se llama el protocolo Schnorr . La generación de clave pública es la multiplicación de un punto base por alguna clave secreta. El protocolo Schnorr demuestra que la clave secreta que se utilizó para generar la clave pública se utilizó para multiplicar la contraseña del usuario por el mismo número. Este protocolo ha sido durante mucho tiempo, se usa mucho donde y le permite probar. Esto se llama prueba a prueba de cero : el servidor no muestra su clave pública, pero dice que la operación que realicé fue realizada por esa clave privada, que acordamos originalmente.

¿Cuáles son las ventajas de este sistema?

Y ella no tiene muchos de ellos.
- El sistema no carga el backend. Debido a que el backend hace todo, convierte la contraseña en un número, la disfraza, la envía y luego desenmascara el resultado también.
- Si le roban una base de datos con tales números, entonces ordenar las contraseñas tampoco tiene sentido sin una clave privada.
- El servicio Pythia puede bloquear los intentos de fuerza bruta, lo que significa que el backend no tiene que hacer esto en principio. Si ve que con el mismo ID de usuario intentan realizar esta operación de transformación varias veces, simplemente puede cortarlo y bloquearlo en el límite de velocidad.
- Gracias al disfraz, el servicio no sabe nada sobre la contraseña. Cada vez que se le envía un nuevo número aleatorio. Solo el identificador de usuario permanece constante.
- Gracias a ZKP (prueba de conocimiento cero), el backend siempre sabe que fue el servicio con el que se había puesto en contacto.
- Si tiene una base de datos con hashes y sal, por ejemplo, puede migrar a esa solución sin problemas para los usuarios. Puede que ni siquiera noten nada. En lugar de la contraseña del usuario, toma su hash, lo conduce a Pythia y en el futuro solo usa este protocolo, obtiene el número
y , vuelve a ponerlo en tu base de datos. El hash se puede eliminar. Cada vez que un usuario inicia sesión en su sistema, se ejecutará este protocolo, como resultado se obtendrá un número que comparará con lo que está en la base de datos. El sistema de autenticación en sí permanecerá sin cambios, ya que los usuarios iniciarán sesión antes e iniciarán sesión, con las mismas contraseñas, incluso las débiles. En este caso, el sistema será mucho más seguro.

Pero estas no son todas las golosinas.

Una de las características principales es que incluso si el servicio Pythia está pirateado, es posible generar una nueva clave privada. En nuestra base de datos, se almacena un número, no un hash. Si representamos la clave anterior como el número k y la nueva como el número k' , entonces podemos calcular un número llamado token de actualización. Para hacer esto, multiplicamos el nuevo número por el número inverso al anterior. Y con este token de actualización, puede revisar la base de datos de cada usuario y multiplicar este número y por el token de actualización. Después de hacer esto, su sistema continúa trabajando con la nueva clave privada en el servicio remoto. Todo sucede al instante. Si ocurre un desastre, le roban su base de datos con contraseñas, libera el token de actualización con el clic de un dedo y el hecho de que los piratas informáticos le roben se vuelve instantáneamente inútil. Simplemente recorre en silencio todos los registros en segundo plano, los actualiza y funcionan con la nueva clave secreta para usted. Los usuarios generalmente ni siquiera notan nada. Es decir La actualización sin problemas y la invalidación instantánea de la base de datos de contraseñas son algunas de las características innovadoras clave de este sistema.

Pero eso no es todo.

El número que se encuentra en la base es grande y , básicamente es grande y se ve bastante pseudoaleatorio, es decir Es muy fácil no recogerlo. Si transferimos la funcionalidad que tenemos en el backend, por ejemplo, a dispositivos cliente, a teléfonos, entonces podemos usar esta y para generar claves. Llamamos a esto BrainKey. Esto significa que el usuario ingresa la contraseña en algún lugar del teléfono, también la oculta y la envía al servicio remoto. El servicio le devuelve un cierto número y y luego puede usar este y para generar algunas claves asimétricas. Por lo tanto, el usuario de su contraseña puede obtener un par de claves. Esto se usa en todo tipo de BrainWallets . Esto es cuando ingresas la contraseña y obtienes la billetera bitcoin generada por ella. Pero esta aplicación no se limita a las criptomonedas, es una firma digital, algunas copias de seguridad y recuperación de cuenta, es decir. donde se usa la criptografía asimétrica, donde se necesitan claves asimétricas. Se puede utilizar todo esto, pero al mismo tiempo se puede generar un par de claves y, según la necesidad, se pueden generar tantas como desee. Por lo tanto, todos dependerán de la contraseña del usuario, y esto es muy conveniente.

En un barril de miel, no es sin una mosca en la pomada.

Y las características de esta tecnología es que es muy nueva. Utiliza una curva elíptica, que es para operaciones bilineales ( BLS12-381 ). Las matemáticas en sí han existido durante algún tiempo, pero esta curva particular, que se usa en particular en nuestra implementación, solo se usa en ZCash, excepto nosotros. En consecuencia, las bibliotecas que usan estas nuevas matemáticas se pueden contar con los dedos de una mano. Para llevar esto al estado de producción, debe dedicar una cierta cantidad de tiempo y esfuerzo. Sin embargo, la industria no se detiene y todas estas desventajas son temporales. Como consecuencia de las dos primeras propiedades, la velocidad de estas operaciones bilineales no es muy consistente con las matemáticas modernas, en particular elípticas, que todos usamos ahora, cuando usamos el protocolo TLS, cuando usamos algunos sitios. Esto es alrededor de varios cientos de operaciones en un servicio en un núcleo. De hecho, esto no nos detuvo y en la primavera implementamos este protocolo, lo lanzamos en producción y tradujimos todos nuestros registros, los protegemos usando este protocolo. En principio, estamos satisfechos con el rendimiento de nuestras tareas actuales, si es necesario, levantaremos otro nodo con el servicio Pythia y, en principio, ya puede jugar con todo esto.
PHE

¿Pero pensamos si podemos hacerlo aún mejor? ¿Es posible lograr las propiedades que Pythia proporciona usando las matemáticas de ayer? No mañana, no hoy, sino incluso ayer, que se ha utilizado durante muchos años.

Y, literalmente, en julio de este año, los científicos lanzaron un nuevo protocolo llamado Simple Password-Hardened Encryption Services, o PHE para abreviar.

Este es Russell Lai , un científico de Europa.
¿Cuál es la ventaja de este servicio? En primer lugar, utiliza la curva P-256 estándar, que se usa en todas partes, en todos los navegadores, productos, en todas partes, la curva predeterminada, que ha existido durante muchos años. En segundo lugar, esta cosa funciona aproximadamente 10 veces más rápido que Pythia y utiliza primitivas estándar. Es un poco difícil, pero puede implementarlo con sus propias manos sin usar bibliotecas oscuras. Puedes usar OpenSSL , o Bouncy Castle , cualquier cosa.

Pero funciona un poco diferente. Nuevamente hay un backend, hay un servicio de PHE. El backend tiene una clave pública, el servicio tiene una clave privada y . A diferencia de Pythia, el proceso de registro y el proceso de verificación de contraseña son un poco diferentes. Cuando un nuevo usuario llega al servicio y quiere registrarse, ¿qué hace el backend? Desde el principio, le pidió al servicio PHE, por favor, deme algunos datos que pueda usar para registrarme, algún tipo de registro de inscripción. El servicio dice OK y responde al backend con las siguientes cosas. Genera algo de sal aleatoria de 32 bytes ( sNonce ). Basado en esta sal y su clave privada y, genera dos números, llamémoslos C0 y C1 . También genera pruebas ( Proof ) de que estos dos números o 2 puntos se generaron precisamente utilizando su clave privada y , utilizando el protocolo Schnorr (como en protocolos anteriores). El backend verifica la Proof . No hay contraseña aquí todavía. ¿Qué hace el backend? Por su parte, también tiene su propia clave privada de cliente personal x y, después de recibir la contraseña del usuario, hace casi lo mismo que el servicio, solo agrega la contraseña allí. Toma cNonce aleatorio (sal de cliente aleatorio), una contraseña, y nuevamente genera 2 números HC0 y HC1 . ¿Por qué 2? Porque el primer HC0 usa para la autenticación, y el segundo número HC1 mezcla algún número aleatorio M multiplicado por la clave privada x ( MC ). El número M también tiene un tamaño de 32 bytes y luego se puede utilizar para cifrar los datos del usuario (tenemos Servicios de cifrado) ( nota del autor de la nota: la clave de cifrado en este caso será MC ). El número MC estará disponible como clave solo después de que el usuario haya ingresado la contraseña correcta. Resulta que en la etapa de registro puede generar no solo un registro de autorización, sino también una clave de cifrado, única para cada usuario, con la que puede cifrar su perfil, algunos datos y algo más. Luego, el backend simplemente suma lo que envió el servicio y lo que hizo: suma estos puntos y obtiene T0 y T1 . En el primer caso, suma dos ( C0 + HC0 ), y en los segundos tres ( C1 + HC1 + MC ). Y pone en la base 2 sales ( sNonce , cNonce ), con la ayuda de la cual se obtuvieron estos números y 2 números ( T0 y T1 ), que resultaron como resultado de la suma.

En consecuencia, el proceso de autenticación del usuario ocurre en el orden inverso. El usuario ingresa su contraseña en el backend. El backend calcula HC0 y, a partir de lo que tiene en la base de datos, resta HC0 de T0 y envía el C0 resultante al servicio junto con la sal del servidor. El servicio, al conocer la sal del servidor, calcula el mismo punto en sí mismo y mira, coincide con el hecho de que envió el backend o no, si coincide, la contraseña es correcta y puede responderla con el segundo número C1 , que restará junto con HC1 del número T1 y obtenga la clave de cifrado. Por lo tanto, la contraseña del servicio PHE ni siquiera desaparece. Ni siquiera deja el backend. Tiene la forma de algunos puntos multiplicados por la clave privada del backend. Ni siquiera existe como tal, pero al mismo tiempo, el servicio remoto puede llegar a una conclusión estricta sobre si esta contraseña es correcta o no, y para demostrar con eso que realizó todos los cálculos utilizando su clave privada y .

¿Qué características tiene este sistema?

La contraseña, como dije, no deja el backend. Pero a diferencia de Pythia, necesita una clave privada en el backend. Bueno, necesitamos y necesitamos, guardar en alguna parte. PHE tiene todas las funciones básicas de Pythia:
- También puede emitir un token de actualización si algo le sucedió con la clave privada;
- También puede revisar toda la base de datos, actualizar y todo estará como estaba;
- protección de búsqueda;
- el servicio no sabe nada sobre la contraseña;
- (Pythia , , , , PHE );
- .

...
… . . passw0rd.io . password , 18- , , zero trust, .. . , , .. Let's encrypt . , . CLI , . 2 SDK , GO .Net, .

:
- .
- .
- .

, .
?
37. ?

.
Q: , ! . , Pythia update token, ? private key . update token? O no?
A: , update token- .
Q: . - update token-, Private key ?
A: , update token-, , - , , , update token. , .. .
Q: , , , .
A: .. .
Q: , , , - Pythia - , , , ?
A: .
Q: ?
A: , Pythia . Es decir , .
Q: ( ) bcrypt ?
A: , , , .
Q: , . ? , …
A: password
Q: password ? Fuego! En general
A: 123456 , 12345, 123456.
Q: . Pythia , PHE .
A: , .
Q: . . ? production ?
A: . ! Pythia.
Q: Pythia, , ?
A: .
Q: , ?
A: .
Q: , , !
A: SDK, .
Q: , , , , .. - , ? ? ?
A: , , , .. PHE, , 5 2 , 2 5 . , . PHE ( , ), , 10 , .
Q: .. - , - ? ?
A: . rate limiting, , .
Q: .. , ?
A: .
Q: . , .. Pythia (), , ? ?
A: , , .
Q: , update ?
A: , Pythia , , - - , , , )
A: ? ! . , , PHE, , .
Conclusiones
PHE ( ) + — ( , , ) ( ). PHE , .
:
, .
Scratch Virgil Security , , !
( )?
UPD : Scratch . . , . .