Hola, pilas completas, entrenemos las habilidades. Sugiero amasar el giro, me parece, es interesante hacer esto usando un paradigma diferente e inusual. La mayoría de los desarrolladores tienen una habilidad desarrollada de algoritmo: la tarea se convierte en ladrillos que deben conectarse, para pensar en la secuencia de movimientos que lleva a la conclusión deseada.
Aquí, hace una semana, se mencionó el Prólogo, me gustaría responder que el lenguaje Prólogo es adecuado para resolver problemas. Ya mencioné este tema, y cité varias soluciones de tareas aleatorias disponibles para mí desde un sitio con tareas para algoritmos , me gustaría mostrar que cualquier solución compleja está disponible en un lenguaje declarativo, y no puede funcionar más lentamente (bueno, tal vez notablemente no muy lento)
Me tomó mucho tiempo llegar a presentar el siguiente problema, y la primera solución ya se recibió, demuestro el problema y descubro qué tan lento es.
El prólogo es interesante porque puede crear un programa deductivo que muestre muchas soluciones e incluso puede limitarlo, pero no proporciona una forma de iterar,
el algoritmo será desarrollado solucionador intérprete
Entonces, la tarea es esta :
- Atrapando agua de lluvia ii
Dada una matriz mxn de enteros positivos que representa la altura de cada celda unitaria en un mapa de elevación 2D, calcule el volumen de agua que puede atrapar después de llover.
Nota:
Tanto myn son menores que 110. La altura de cada celda unitaria es mayor que 0 y menor que 20,000.
Ejemplo:
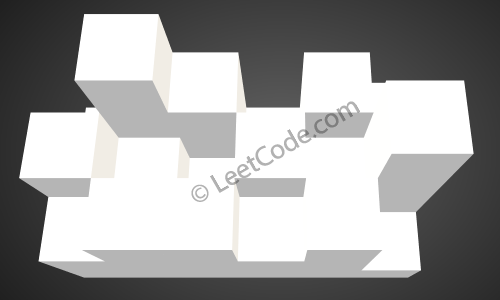
Dado el siguiente mapa de altura 3x6:
[
[1,4,3,1,3,2]
[3,2,1,3,2,4]
[2,3,3,2,3,1]
]
Regreso 4.
Después de largos intentos de formular una solución, llegué a esta redacción:
Es necesario verter un máximo de agua en cada celda, que no se derramaría . Sugiero verter una cierta cantidad de agua en cada celda, pero para que sea menor que el valor máximo posible.
Resultó así:
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.
Este predicado toma la lista de entrada (matriz) y la convierte en una solución, en una matriz en la que hay otros valores que serán una respuesta válida. Luego, otro predicado toma estas dos listas elemento por elemento y encuentra la cantidad total.
repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).
este predicado tomará una de las soluciones y verificará si está "normalmente" lleno, si satisface la condición del problema, entonces esta es la solución.
Este es el método de "generar y verificar", decimos que el valor está en dicho conjunto y revisamos todos los elementos de este conjunto, verificando algún tipo de condición de salida.
Entonces, obtendré una nueva solución con el predicado put (Vals, X0, X1), aquí, en primer lugar, hay una lista de todas las alturas posibles que se encuentran en esta matriz, de la cual seleccionaremos las alturas posibles para cada celda. Según el análisis de las pruebas de entrada, se descubrió que en este problema es posible llenar toda la celda, si se puede insertar tanta agua a su alrededor que se vierte "sobre la cabeza".
En total, este predicado parece más complicado, es necesario procesar los triples de las líneas que conforman un cuadrado de 3x3 (sí, no hay una matriz en el Prolog, pero parece la descripción de los datos de entrada, por lo que lo usamos en la programación declarativa, es posible que no conozca los índices de elementos en la matriz , solo hay una lista con su encabezado y cola, así que solo describa una plantilla que coincida con la especificación de entrada).
puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).
Así es como resulta expresar un bypass de la matriz, desde el cual puede tomar las primeras tres (y más) filas, de las cuales, también puede seleccionar, de izquierda a derecha, triples de elementos, y entre los ocho vecinos habrá una celda [Itaya] [Utaya] del paisaje. Con la ayuda de sel_biger (R2, V, R21) se crea un nuevo significado de esta celda.
Este valor se puede establecer en la celda actual, puede ser una de las alturas posibles, e incluso la lista se ordena en orden descendente, de modo que la primera será la altura más alta que esté disponible, y luego cualquier siguiente:
sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).
Era una descripción de un "generador de decisiones", y luego debe asegurarse de que la matriz obtenida, a partir de las alturas rellenadas arbitrariamente en cada punto, sea similar a la respuesta que requerimos.
Y fue necesario encontrar un estado tal que el agua se asiente en los agujeros, intentaré decirlo de esta manera:
de nueve valores de un cuadrado es tres por tres, en el centro siempre debe haber una altura tal que no contradiga el mapa de entrada, por lo que no se obtuvo el cambio de equilibrio que originalmente estaba en estas celdas, si había una altura, entonces no debería haber celdas encima, incluso si todo se inundará con agua, entonces aquí podemos decir que la celda alta debe permanecer sola o ser reemplazada por un valor más alto, pero de modo que sea igual a todos los vecinos, es decir las celdas a la izquierda, a la derecha y de arriba a abajo de la corriente deben exceder o ser iguales, si hay más agua en la celda, solo si ha aumentado alrededor ...
Y los dos predicados finales, que toman la matriz de entrada, comienzan la búsqueda de un resultado adecuado, restan la suma de los elementos entre ellos y encuentran la suma final que se requería en el problema:
diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %% , sums(X,S):-reptest(X,X1),diffall(X,X1,S).
Demostraré las pruebas que ha proporcionado el sitio .
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). % balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). % , 33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). % , % equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).
Tuve que comentar sobre las pruebas. No todo pasó.
La tarea es cómo acelerarlo?
Algunas soluciones no se pueden encontrar, debido a una larga búsqueda de soluciones, se generan demasiado lentamente en este orden, aquí la complejidad es probablemente n!, Se ordenan todos los valores posibles para cada celda de la matriz.
Es conveniente expresar esta tarea en un sistema de programación en restricciones, solo en el Prolog se llama así: CLP (FD): programación de lógica de restricción sobre dominios finitos.
clp (fd) es una biblioteca incluida en la distribución estándar SWI-Prolog. Resuelve problemas que involucran conjuntos de variables, donde las relaciones entre las variables necesitan satisfacerse.
>>
Formulo el problema así:
Necesitamos dicha lista, cada elemento del conjunto de valores mayor o igual que su valor máximo en todo el mapa, teniendo en cuenta la limitación de que los elementos deben ubicarse claramente en el orden del líquido derramado correspondiente.
Así es como lo estoy haciendo desde la lista de entrada, una nueva lista cuyos elementos se han vuelto desconocidos en un rango dado (desde el valor R2 del elemento actual hasta el valor Máximo de V)
En la entrada, una lista de listas; en la salida, una nueva lista con la distribución máxima de valores,
que satisfacen la limitación de balns de "equilibrio de fluidos":
checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Esto es tanto un generador como una verificación al mismo tiempo, se indica que los elementos están en dicho conjunto, y luego, aplicando gradualmente una verificación, este conjunto se reduce. Además, queda algo y puede ser "marcado", es decir establecer valores enteros que satisfagan la suma de todas las restricciones. Llamar al etiquetado ([abajo], FX2) obliga a llenar (contacto) variables desconocido con valores específicos, y puede haber varias opciones de este tipo, pero siempre tomaremos la primera, ya que se dijo que todas las variables se mueven hacia abajo en la búsqueda, desde sus límites superiores, estas son las opciones de búsqueda [hacia abajo].
Y allí puede ver configuraciones tan complejas como:16.2.1. estrategia de selección variable
La estrategia de selección de variables le permite especificar qué variable de Vars se etiqueta a continuación y es una de:
a la izquierda: etiquete las variables en el orden en que aparecen en Vars. Este es el valor predeterminado.
ff Primero falla. Etiquete la variable más a la izquierda con el dominio más pequeño a continuación, para detectar la inviabilidad temprano. Esta suele ser una buena estrategia cuando hay dominios pequeños para las variables subsiguientes cuando se elige una primera variable.
ffc De las variables con dominios más pequeños, el más a la izquierda que participa en la mayoría de las restricciones se etiqueta a continuación. La aplicación de una restricción tiene que eliminar un subárbol, por lo que puede ser una buena estrategia.
min Etiqueta la variable más a la izquierda cuyo límite inferior es el más bajo al lado. tenga en cuenta que esto es min / 0, diferente de min / 1, que determina la solución solución y se discute en la sección anterior anterior. Esta es una buena táctica si está tratando de minimizar algún valor global que probablemente sea menor si varias variables lo son (por ejemplo, una solución de costo mínimo).
max Etiqueta la variable más a la izquierda cuyo límite superior es el siguiente más alto. Esto también es diferente de max / 1. Y el consejo para min se aplica a max cuando se trata de maximizar un valor global.
16.2.2. orden de valor
El orden de valor es uno de:
subir Pruebe los elementos del dominio de la variable elegida en orden ascendente. Este es el valor predeterminado.
down Pruebe los elementos del dominio en orden descendente.
Obviamente, si tiene una distribución asimétrica, como demostramos en cómo etiquetar eficientemente arriba, pruebe los elementos en el primer orden más común.
16.2.3. estrategia de ramificación
La estrategia de ramificación es una de:
paso Para cada variable X, se hace una elección entre X = V y X # \ = V, donde V está determinado por las opciones de orden de valor. Este es el valor predeterminado.
enumeración Para cada variable X, se hace una elección entre X = V_1, X = V_2, etc., para todos los valores V_i del dominio de X. El orden está determinado por las opciones de orden de valores.
bisección Para cada variable X, se elige entre X # = <M y X #> M, donde M es el punto medio del dominio de X. Elija esta opción si muchas variables son selecciones entre un rango de enteros, un valor, en lugar de uno entre un conjunto de valores enumerados (por ejemplo, porcentajes, vs a = 0, b = 1, c = 2)
Ahora, en realidad, lo que está "equilibrado" es cuando el agua vertida no se desborda de una celda a otra. Esta es la correspondencia del orden inicial de los elementos. Uno podría pensar que llenar las celdas conservará la forma del paisaje original, lo que significa que si hubiera un muro, entonces se puede cubrir con agua en la parte superior, de modo que se vuelva necesariamente igual a todos sus vecinos, o si no es un muro cubierto con agua ...
Considere las situaciones equilibradas:
-Si la celda se inunda, entonces al lado de la misma o incluso más alta (de repente es la pared).
-Si la celda era igual a la vecina, entonces debería ser igual a la nueva vecina.
-Y en el caso extremo, la celda no cambió su significado, y aún qué tipo de vecinos tenía:
Así es como puedes transferir tu actitud a la tarea al programa. No es necesario que piense en un algoritmo de decisión, es importante proporcionar una descripción correcta del resultado, establecer correctamente todas las restricciones iniciales (conjuntos de valores). Este enfoque puede simplemente "mezclarse" con la búsqueda habitual con retorno y recurrencia inherentes a Prolog. Esta es una forma de formular aún más programas declarativos que utilizando los métodos clásicos de Prolog.
Daré la solución obtenida, con un conjunto de pruebas:
:- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Y mas pruebas :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).
Estas fueron pruebas del sitio, solo las primeras 30 piezas. El resultado es excelente, el problema se resuelve, e incluso rápidamente, todo el tiempo hasta un segundo.
Puedes consultar ...
Como conclusión
La programación declarativa implica una formalización detallada de la tarea, y el solucionador buscará la solución más efectiva que satisfaga las condiciones.
Un poco más profundo en el tema, puede abrir minizinc , un lenguaje de programación en el que está incrustado este paradigma. Formularon muchos significados, indicaron restricciones y, voila, la respuesta. Resuelven Sudoku , tareas de coloreado de mapas, trabajo de programación , problemas de recursos, programación. Sugiero entrenar ...