Considere pronosticar series de tiempo. Tratemos de predecir gráficos de cotizaciones, o algo más que resulte útil.
Tomemos como base el pronóstico presentado en el artículo
El modelo de pronóstico de series temporales para la muestra de máxima similitud: explicación y ejemplo (este artículo no es mío). El breve punto es que el segmento más similar del gráfico se busca a la izquierda del pronóstico entre la historia pasada y, a partir de este viejo mejor, los valores a la derecha del gráfico se toman y se usan como pronóstico.
Iré más lejos Al calcular el pronóstico, no tomaré un caso que sea el mejor en correlación, sino un paquete de los mejores. Y el pronóstico será el promedio de los resultados de este paquete. Esto permitirá comprender que el valor encontrado es una regularidad, y no una coincidencia accidental con el pronóstico deseado, o una desviación aleatoria si el pronóstico se desvía del real.
Usar la mejor opción como en ese artículo no es correcto, así como determinar la distribución de probabilidad con un valor de esta distribución. Si genera un gráfico muy grande de datos aleatorios y comienza una búsqueda en ellos, entonces seguramente habrá segmentos correlacionados en ellos, e incluso posiblemente con un coeficiente de 0.9999, pero no es necesario que segmentos similares sigan estos segmentos aún más, todavía es Todo es al azar. Y debe tomar solo un paquete de dichos segmentos y calcular que la varianza de los datos posteriores es menor que la varianza que se forma a partir de una muestra aleatoria de estos datos. Y si la dispersión del paquete es menor, entonces este es el pronóstico. Aunque esto tampoco es una representación precisa de posibles errores, esto es suficiente por ahora.
Es decir
El pronóstico no
es el principio del muestreo y la correlación de los segmentos comparados que utilizamos, lo principal es que, como resultado de la aplicación de esta muestra, la varianza de los valores deseados sería menor que como resultado del muestreo aleatorio.
Además, la variación de este paquete permitirá evaluar cuál es mejor usar la opción de selección de casos anteriores. Después de todo, es posible seleccionar no siempre un segmento de datos de correlación, y no siempre usar la correlación de Pearson. Y tal elección se puede hacer para cada punto pronosticado por separado. Para qué tipo de muestra la varianza es menor, esa opción es mejor para el punto actual.
¿Qué tamaño de paquete debe ser? Esto se basa en el tema de los intervalos de confianza. Para no cargar mucho, hay una mención de que es mejor tomar al menos 30 ejemplos para determinar el valor promedio. Si hay un exceso de datos de prueba, tomaría al menos 100.
La relación de las desviaciones estándar de la muestra de acuerdo con el algoritmo y la aleatoria se puede llamar coeficiente de éxito teórico del algoritmo de pronóstico para el punto actual para fines de comparación con otros algoritmos de muestreo, o para determinar la utilidad de este pronóstico en general, mientras que el valor real aún no está disponible.
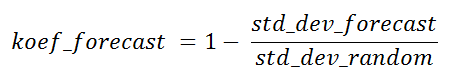
Este coeficiente puede en algunos casos tomar valores negativos. Los puntos en los que ocurre esto son de poco interés, al igual que los puntos con un coeficiente cero. En el caso de 100% de previsibilidad, será igual a uno.
Pasemos a ejemplos prácticos, nuevamente de ese artículo. Después de corregir los pequeños errores allí, obtenemos el siguiente resultado, consistente con ese artículo y ese algoritmo:
cálculo de la previsión en el momento del 1/9/2012 23:00 posición 52631
valores totales verificados para similitud 2184
la mejor correlación 0.958174 posición 52295
coeficientes de transferencia alfa (1/2) 1.03117 -11.1992
error de pronóstico de hecho mape 5.210%mape - el término del artículo original Error porcentual absoluto medio, se calcula mediante la fórmula
Abs (Pronóstico - Hecho) / HechoY ahora hagamos una selección de no una mejor similitud, sino paquetes de lo mejor y todo para predecir un momento en el tiempo y ver qué sucede:
0 corr 0.958174 pos 52295 mape 5.210%
1 corr 0.953571 pos 52151 mape 6.566%
2 corr 0.953532 pos 45599 mape 11.642%
3 corr 0.951462 pos 45743 mape 7.033%
4 corr 0.950921 pos 45575 mape 3.300%
5 corr 0.950789 pos 38687 mape 3.538%
El valor de correlación aquí cambia de valor a valor insignificante. Al mismo tiempo, el valor del resultado del pronóstico varía del 3% al 11%. Es decir ese 5% inicial no es más que una coincidencia, podría ser el 11% y el 3%.
Bajo las condiciones de similitud especificadas en ese artículo, los valores de 2184 se pueden comparar en total. De estos, tomé un paquete de los mejores en 1500 piezas, ordenados en orden de disminución de la correlación, y lo mostré en un gráfico. La correlación en este paquete de los mejores 0.958 cayó a 0.715 de izquierda a derecha. Pero la fluctuación del resultado prácticamente no cambió:

Se puede ver que la dependencia del resultado de la correlación es muy baja, pero no obstante parece estar allí. En general, tomamos un paquete de los 100 valores principales y calculamos el pronóstico, como mencioné, por el promedio de este paquete. El resultado es el siguiente:
mape 5.824%, stddev mape 7.035% . Pero este 5.8% ya no es una coincidencia, sino el promedio de la distribución, el pronóstico más probable. La desviación estándar del mape es mayor que el mape en sí, pero esto se debe a que el mape tiene una distribución no simétrica.
También calculé el mismo pronóstico pero usando una muestra condicionalmente aleatoria, más precisamente, simplemente promediada de todas las opciones posibles, el resultado de
mape fue 8.246% . Por muestreo aleatorio, el error es ligeramente mayor, pero este valor todavía está dentro del rango de dispersión calculado a partir de la mejor muestra. Para el punto calculado, el coeficiente de pronóstico teórico indicado por mí es cercano a cero, más precisamente
koef_forecast = -0.041 . No lo conté desde stddev mape (incluye el pronóstico real), sino a partir de los valores absolutos del pronóstico, si nos fijamos en el programa, los números iniciales se dan allí.
Pero esto es si se trata de la marca de tiempo, que se mencionó en el artículo original. Pero si consideramos “9/4/2012 23:00” (mes / día / año), el coeficiente teórico de eficiencia es
koef_forecast = 0.21 y
mape = 3.126%, mape_rand = 7.147% . Es decir koef_forecast mostró de antemano que el punto actual se calculará con mayor precisión que el anterior. La esencia de la utilidad de este coeficiente es que al menos de alguna manera puede evaluar el resultado incluso antes de obtener los datos reales, porque los datos reales no participan en ella. Cuanto más alto sea, mejor. Ya mencioné que un punto absolutamente predicho tendrá un coeficiente de uno.
Usted mismo puede ver cómo cambian todos estos números en mi programa de demostración en Qt C ++, allí puede elegir la fecha y el tamaño del paquete: las
fuentes en githubLos mejores valores se seleccionan de acuerdo con el siguiente algoritmo:
inline void OrdPack::add_value(double koef, int i_pos) { if (std::isfinite(koef)==false) return; if (koef <= 0.0) return; if (mmap_ord.size() < ma_count_for_pack) { if (mmap_ord.size()==0) mi_koef = koef; mi_koef = std::min(mi_koef, koef); mmap_ord.insert({-koef,i_pos}); } else if (koef > mi_koef) { mmap_ord.insert({-koef,i_pos}); while (mmap_ord.size() > ma_count_for_pack) mmap_ord.erase(--mmap_ord.end()); mi_koef = -(--mmap_ord.end())->first; } }
No tiene sentido publicar toda la fuente aquí, no es complicado allí, y con comentarios. La base en el procedimiento MainWindow :: to_do_test () en el archivo
mainwindow.cpp .
Por ahora, seguiré intentando predecir algo en la siguiente parte.
PS. Por favor, deje sus comentarios sobre si todo está claro sobre lo que falta. Ya formé un plan aproximado sobre qué escribir a continuación, pero con sus comentarios lo haré mejor.