Teoría de la felicidad. La estadística como forma científica de no saber nada

Sigo familiarizando a los lectores de Habr con los capítulos de su libro "Teoría de la felicidad" con el subtítulo "Fundamentos matemáticos de las leyes de la maldad". Este libro de ciencia popular aún no se ha publicado, informa de manera muy informal acerca de cómo las matemáticas le permiten mirar el mundo y la vida de las personas con un nuevo grado de conciencia. Es para aquellos que están interesados ​​en la ciencia y para aquellos que están interesados ​​en la vida. Y dado que nuestra vida es compleja y, en general, impredecible, el énfasis en el libro se centra principalmente en la teoría de la probabilidad y las estadísticas matemáticas. Aquí no se prueban los teoremas y no se dan los fundamentos de la ciencia, de ninguna manera es un libro de texto, sino lo que se llama ciencia recreativa. Pero es precisamente un enfoque tan lúdico que nos permite desarrollar la intuición, alegrar las conferencias para los estudiantes con ejemplos vívidos y, por último, explicar a los no matemáticos y a nuestros hijos lo interesante que encontramos en nuestra ciencia seca.


Este capítulo trata sobre estadísticas, clima e incluso filosofía. No te preocupes, solo un poco. No más que se pueda usar para la mesa en una sociedad decente.

Los números son engañosos, especialmente cuando los hago yo mismo; En esta ocasión, la declaración atribuida a Disraeli es cierta: "Hay tres tipos de mentiras: mentiras, mentiras descaradas y estadísticas".
Mark Twain

¡Con qué frecuencia en el verano planeamos salir al aire libre, dar un paseo por el parque o hacer un picnic, y luego la lluvia rompe nuestros planes y nos encarcela en la casa! Y bueno, si esto sucedió una o dos veces por temporada, ¡a veces parece que el clima sigue al fin de semana, llegando al sábado o al domingo una y otra vez!

Investigadores australianos publicaron un artículo relativamente reciente: "Ciclos semanales de temperatura máxima y la intensidad de las islas termales urbanas". Los medios de comunicación la recogieron y reimprimieron los resultados con el siguiente encabezado: “¡No pienses! Los científicos han descubierto que el clima los fines de semana es realmente peor que entre semana ". El documento citado proporciona estadísticas sobre temperatura y precipitación durante muchos años en varias ciudades de Australia, y de hecho revela una disminución de la temperatura en ciertas horas del sábado y domingo. Después de eso, se da una explicación que conecta el clima local con el nivel de contaminación del aire debido al aumento del flujo de tráfico. Poco antes de esto, se realizó un estudio similar en Alemania y condujo a aproximadamente las mismas conclusiones.

De acuerdo, las fracciones de un grado es un efecto muy sutil. Quejándonos del mal tiempo del tan esperado sábado, estamos discutiendo si el día era soleado o lluvioso, este hecho es más fácil de registrar y luego recordar, sin siquiera tener instrumentos precisos. Realizaremos nuestro propio pequeño estudio sobre este tema y obtendremos un resultado maravilloso: podemos decir con confianza que no sabemos si el día de la semana y el clima están relacionados en Kamchatka. Los estudios con un resultado negativo generalmente no se incluyen en las páginas de las revistas y en las noticias, pero es importante que usted y yo comprendamos sobre qué base, en general, puedo decir con confianza algo sobre procesos aleatorios. Y a este respecto, un resultado negativo no es peor que uno positivo.

Una palabra en defensa de las estadísticas.

Las estadísticas son culpadas de la masa de pecados: en mentiras y en las posibilidades de manipulación y, finalmente, en incomprensibilidad. Pero realmente quiero rehabilitar esta área de conocimiento, para mostrar cuán difícil es la tarea para la que está destinada y cuán difícil es comprender la respuesta que dan las estadísticas.

La teoría de la probabilidad utiliza el conocimiento preciso de variables aleatorias en forma de distribuciones o cálculos combinatorios integrales. Destaco una vez más que es posible tener un conocimiento preciso de una variable aleatoria. Pero, ¿qué pasa si este conocimiento exacto es inaccesible para nosotros, y lo único que tenemos a nuestra disposición es la observación? El desarrollador del nuevo medicamento tiene un número limitado de pruebas, el creador del sistema de control de flujo de tráfico solo tiene una serie de mediciones en el camino real, el sociólogo tiene los resultados de las encuestas, además, puede estar seguro de que al responder algunas preguntas, los encuestados solo mentí

Está claro que una observación no da nada en absoluto. Dos, un poco más que nada, tres, cuatro ... cien ... ¿cuántas observaciones necesita para conocer alguna variable aleatoria de la que pueda estar seguro con precisión matemática? ¿Y qué tipo de conocimiento será? Lo más probable es que se presente en forma de una tabla o un histograma que permita evaluar algunos parámetros de una variable aleatoria; se denominan estadísticas (por ejemplo, dominio de definición, media o varianza, asimetría, etc.). Quizás mirar el histograma podrá adivinar la forma exacta de la distribución. Pero atención! - ¡todos los resultados de la observación serán variables aleatorias! ¡Mientras no tengamos un conocimiento preciso de la distribución, todos los resultados de la observación nos dan solo una descripción probabilística del proceso aleatorio! Una descripción aleatoria de un proceso aleatorio aún no se confundiría aquí, ¡ni siquiera querría confundir intencionalmente!

¿Qué hace que las estadísticas matemáticas sean una ciencia exacta? Sus métodos nos permiten concluir nuestra ignorancia en un marco claramente limitado y dar una medida computable de confianza de que, dentro de este marco, nuestro conocimiento es consistente con los hechos. Este es el lenguaje en el que se puede razonar sobre variables aleatorias desconocidas para que el razonamiento tenga sentido. Tal enfoque es muy útil en filosofía, psicología o sociología, donde es muy fácil participar en largos razonamientos y discusiones sin ninguna esperanza de obtener conocimientos positivos y, especialmente, pruebas. Se dedica mucha literatura al procesamiento de datos estadísticos competentes, porque es una herramienta absolutamente necesaria para médicos, sociólogos, economistas, físicos, psicólogos ... en resumen, para todos los científicos que investigan el llamado "mundo real", que difiere del matemático ideal solo en el grado de nuestra ignorancia al respecto.

Ahora eche otro vistazo al epígrafe de este capítulo y comprenda que las estadísticas, que tan despectivamente se llaman tercer grado de mentiras, son las únicas cosas que tienen las ciencias naturales. ¡No es esta la ley principal de la maldad del universo! Todas las leyes de la naturaleza que conocemos, desde las físicas hasta las económicas, se basan en modelos matemáticos y sus propiedades, pero se verifican por métodos estadísticos durante las mediciones y observaciones. En la vida cotidiana, nuestra mente hace generalizaciones y observa patrones, aísla y reconoce imágenes repetidas, esto es probablemente lo mejor que puede hacer el cerebro humano. Esto es exactamente lo que la inteligencia artificial está enseñando en estos días. Pero la mente ahorra su fuerza y ​​se inclina a sacar conclusiones de observaciones individuales, sin preocuparse mucho por la precisión o validez de estas conclusiones. En esta ocasión, hay una maravillosa declaración coherente del libro de Stephen Brast, Isola: "Todos extraen conclusiones generales de un ejemplo. Al menos yo hago exactamente eso . Y mientras hablamos de arte, la naturaleza de las mascotas o hablamos de política, no puede preocuparse mucho por esto. Sin embargo, al construir un avión, organizar un servicio de despacho en el aeropuerto o probar un nuevo medicamento, ya no puede referirse al hecho de que "me parece", "la intuición dice" y "todo sucede en la vida". Aquí debe limitar su mente al marco de rigurosos métodos matemáticos.

Nuestro libro no es un libro de texto, y no estudiaremos métodos estadísticos en detalle y nos limitaremos a una sola cosa: la técnica de probar hipótesis. Pero me gustaría mostrar el curso del razonamiento y la forma de los resultados característicos de este campo de conocimiento. Y, tal vez, algunos de los lectores, el futuro estudiante, no solo entenderán por qué lo atormentan con estadísticas, todos estos diagramas QQ, distribuciones t y F, sino que surgirá otra pregunta importante: ¿cómo es posible saber qué? - Seguramente sobre un accidente? ¿Y qué aprendemos exactamente usando estadísticas?

Tres ballenas de estadísticas

Los principales pilares de la estadística matemática son la teoría de la probabilidad, la ley de los grandes números y el teorema del límite central .

La ley de los grandes números, en una interpretación libre, sugiere que un gran número de observaciones de una variable aleatoria casi con certeza refleja su distribución , por lo que las estadísticas observadas: promedio, varianza y otras características tienden a valores exactos correspondientes a la variable aleatoria. En otras palabras, el histograma de los valores observados con un número infinito de datos casi seguramente tiende a la distribución que podemos considerar como cierta. Es esta ley la que conecta la interpretación de frecuencia "cotidiana" de la probabilidad y lo teórico, como medidas en un espacio de probabilidad.

El teorema del límite central, nuevamente, en una interpretación libre, dice que una de las formas más probables de distribución de una variable aleatoria es una distribución normal (gaussiana). La redacción exacta suena diferente: la distribución normal describe el valor promedio de un gran número de variables aleatorias reales distribuidas de forma idéntica, independientemente de su distribución. Este teorema generalmente se prueba utilizando métodos de análisis funcionales, pero veremos más adelante que se puede entender e incluso expandir introduciendo el concepto de entropía como una medida de la probabilidad de un estado del sistema: una distribución normal tiene la mayor entropía con el menor número de restricciones. En este sentido, es óptimo cuando se describe una variable aleatoria desconocida, o una variable aleatoria, que es una combinación de muchas otras variables, cuya distribución también es desconocida.

Estas dos leyes subyacen a las estimaciones cuantitativas de la fiabilidad de nuestro conocimiento basado en observaciones. Aquí estamos hablando de confirmación estadística o refutación de la suposición, que puede hacerse a partir de algunos fundamentos comunes y modelos matemáticos. Esto puede parecer extraño, pero en sí mismo, las estadísticas no producen nuevos conocimientos. Un conjunto de hechos se convierte en conocimiento solo después de construir conexiones entre hechos que forman una determinada estructura. Son estas estructuras y relaciones las que nos permiten hacer predicciones y suposiciones generales basadas en algo que va más allá de las estadísticas. Tales suposiciones se llaman hipótesis . Es hora de recordar una de las leyes de la merfología, el postulado de Persigue :

El número de hipótesis razonables que explican cualquier fenómeno es infinito.

La tarea de la estadística matemática es limitar este número infinito, o más bien reducirlos a uno, y no necesariamente es cierto en absoluto. Para pasar a una hipótesis más compleja (y a menudo más deseable), es necesario, utilizando datos de observación, refutar la hipótesis más simple y más general, o reforzarla y abandonar el desarrollo de la teoría. La hipótesis a menudo probada de esta manera se llama nula , y hay un sentido profundo en esto.

¿Qué puede actuar como una hipótesis nula? En cierto sentido, cualquier cosa, cualquier afirmación, pero con la condición de que pueda traducirse al lenguaje de medición. Muy a menudo, la hipótesis es el valor esperado de algún parámetro, que se convierte en una variable aleatoria durante la medición, o la ausencia de una conexión (correlación) entre dos variables aleatorias. A veces se supone el tipo de distribución, un proceso aleatorio, se propone algún modelo matemático. La formulación clásica de la pregunta es la siguiente: ¿las observaciones nos permiten rechazar la hipótesis nula o no? Más precisamente, ¿con qué certeza podemos decir que las observaciones no pueden obtenerse sobre la base de la hipótesis nula? Además, si no pudimos probar, en base a datos estadísticos, que la hipótesis nula es falsa, entonces se acepta como verdadera.

Y aquí podría pensar que los investigadores se ven obligados a cometer uno de los errores lógicos clásicos, que lleva el sonoro nombre latino ad ignorantiam. Este es un argumento de la verdad de una declaración, basado en la falta de evidencia de su falsedad. Un ejemplo clásico son las palabras pronunciadas por el senador Joseph McCarthy cuando se le pidió que presentara hechos para respaldar su acusación de que cierta persona es comunista: "Tengo poca información sobre este tema, excepto la declaración general de las autoridades competentes de que no hay nada en su expediente". para excluir sus lazos con los comunistas " . O incluso más brillante: "Bigfoot existe, ya que nadie ha demostrado lo contrario" . Identificar la diferencia entre una hipótesis científica y trucos similares es el tema de todo un campo de filosofía: la metodología del conocimiento científico . Uno de sus resultados sorprendentes es el criterio de falsabilidad presentado por el notable filósofo Karl Popper en la primera mitad del siglo XX. Este criterio está diseñado para separar el conocimiento científico de los no científicos y, a primera vista, parece paradójico:

Una teoría o hipótesis puede considerarse científica solo si existe, incluso hipotéticamente, una forma de refutarla.

¡Qué no es la ley de la maldad! Resulta que cualquier teoría científica es automáticamente potencialmente incorrecta, y una teoría que es verdadera "por definición" no puede considerarse científica. Además, ciencias como las matemáticas y la lógica no satisfacen este criterio. Sin embargo, no se refieren a las ciencias naturales , sino a las formales , que no requieren una prueba de falsabilidad. Y si agregamos un resultado más del mismo tiempo: el principio de incompletitud de Gödel, que establece que dentro de cualquier sistema formal es posible formular una declaración que no se puede probar ni refutar, entonces puede quedar claro por qué, en general, participar en toda esta ciencia. Sin embargo, es importante entender que el principio de falsabilidad de Popper no dice nada sobre la verdad de una teoría, sino solo si es científica o no. Puede ayudar a determinar si una teoría proporciona un lenguaje en el que tiene sentido hablar sobre el mundo o no.

Pero aún así, ¿por qué, si no podemos rechazar la hipótesis sobre la base de datos estadísticos, tenemos derecho a aceptarla como verdadera? El hecho es que la hipótesis estadística no se toma del deseo o las preferencias del investigador, sino que debe seguir las leyes formales generales. Por ejemplo, del Teorema del límite central o del principio de máxima entropía. Estas leyes reflejan correctamente el grado de nuestra ignorancia , sin agregar, innecesariamente, suposiciones o hipótesis innecesarias. En cierto sentido, este es un uso directo del famoso principio filosófico conocido como la navaja de afeitar de Occam :

Lo que se puede hacer sobre la base de menos suposiciones no se debe hacer sobre la base de más.

Por lo tanto, cuando aceptamos la hipótesis nula, basada en la ausencia de su refutación, mostramos formal y honestamente que, como resultado del experimento, el grado de ignorancia se mantuvo en el mismo nivel . En el ejemplo del Bigfoot, explícita o implícitamente, se supone lo contrario: la falta de evidencia de que esta misteriosa criatura no parece ser algo que pueda aumentar el grado de nuestro conocimiento al respecto.

En general, desde el punto de vista del principio de falsabilidad, cualquier declaración sobre la existencia de algo no es científica, porque la falta de evidencia no prueba nada. Al mismo tiempo, la afirmación de la ausencia de cualquier cosa se puede refutar fácilmente proporcionando una copia, evidencia indirecta o demostrando la existencia de una construcción. Y en este sentido, una prueba de hipótesis estadística analiza las alegaciones de la ausencia del efecto deseado y puede, en cierto sentido, proporcionar una refutación precisa de esta afirmación. Esto es exactamente lo que el término "hipótesis nula" está totalmente justificado: contiene el mínimo conocimiento necesario sobre el sistema.

Cómo confundir estadísticas y cómo desentrañar

Es muy importante enfatizar que si las estadísticas indican que la hipótesis nula puede ser rechazada, esto no significa que demostremos la verdad de cualquier hipótesis alternativa. , , , . : , ( $$$\sim 1/7$ ), , II ? , , , «» : , $$$1\%$ , , , $$$98\%$ . $$1000 conductores y dejar$1000$$$100 de ellos estarán realmente borrachos. Como resultado, obtenemos$100$$$900 × 1 % = 9 falsos positivos y$900\times1\%=9$$$100 × 1 % = 1 resultado falso negativo: es decir, para un borracho que entró, habría nueve conductores aleatorios acusados ​​inocentemente. ¡Qué no es la ley de la maldad! La paridad se observará solo si la proporción de conductores ebrios es igual a$100\times1\%=1$$$$1/2$ , . , , !

. , : . , , . : .
La probabilidad de intersección de los eventos A y B se define como el producto de la probabilidad del evento B y la probabilidad del evento. $$A , si se sabe que ha ocurrido un evento$A$$$$B$ :

$$

$$P(A \cap B) = P(B)P(A|B).$$

Ahora puede determinar la independencia de los eventos de tres maneras equivalentes: Eventos $$$A$ y $$B independiente si$B$$$P ( A | B ) = P ( A ) , o$P(A|B) = P(A)$$$P ( B | A ) = P ( B ) , o$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ .
Esto completa la definición formal de probabilidad comenzada en el primer capítulo.

La intersección es una operación conmutativa, es decir$$$P(A\cap B) = P(B\cap A)$ . Esto implica inmediatamente el teorema bayesiano:

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

que puede usarse para calcular probabilidades condicionales.

En nuestro ejemplo con conductores y una prueba de alcohol, tenemos eventos:$$A - el conductor está borracho,$A$$$B - la prueba dio un resultado positivo. Probabilidades$B$$$P ( A ) = 0.1 - la probabilidad de que el conductor parado esté ebrio;$P(A) = 0.1$$$P ( B | A ) = 99 % : la probabilidad de que la prueba dé un resultado positivo si se sabe que el conductor está ebrio (excluido$P(B|A) = 99\%$$$1 % falso negativo)$1\%$$$P ( A | B ) = 99 % - la probabilidad de que la prueba esté borracha, si la prueba dio un resultado positivo (excluido$P(A|B) = 99\%$$$1 resultados falsos positivos). Calculamos$1%$$$$P (B)$ - la probabilidad de obtener un resultado positivo en la carretera:

$$

$$P (B) = \ frac {P (A) P (A | B)} {P (B | A)} = P (A) = 0.1$$

Ahora nuestro razonamiento se ha formalizado y, como saben, quizás para algunas personas sea más comprensible. El concepto de probabilidad condicional le permite razonar lógicamente en el lenguaje de la teoría de probabilidad. No es sorprendente que el teorema de Bayes haya encontrado una amplia aplicación en la teoría de la decisión, en los sistemas de reconocimiento de patrones, en los filtros de spam, en los programas que prueban las pruebas de plagio y en muchas otras tecnologías de la información.

Los estudiantes entienden cuidadosamente estos ejemplos de exámenes médicos o prácticas legales. Pero me temo que ni a los periodistas ni a los políticos se les enseña estadística matemática ni teoría de la probabilidad, pero apelan con entusiasmo a los datos estadísticos, los interpretan libremente y llevan el "conocimiento" adquirido a las masas. Por lo tanto, insto a mi lector: descubrí las matemáticas yo mismo, ¡ayúdame a resolverlo para otro! No veo otro antídoto contra la ignorancia.

Medimos nuestra credulidad

Consideraremos y aplicaremos en la práctica solo uno de los muchos métodos estadísticos: probar hipótesis estadísticas. Para aquellos que ya han vinculado sus vidas a las ciencias naturales o sociales, no habrá algo asombrosamente nuevo en estos ejemplos.

Supongamos que medimos repetidamente una variable aleatoria que tiene un valor promedio $$$\ mu$ y desviación estándar $$$\ sigma$ . Según el Teorema del límite central, el valor medio observado se distribuirá normalmente. De la ley de los grandes números se deduce que su promedio tenderá a $$$\ mu$ , y de las propiedades de la distribución normal se deduce que después $$$n$ medida, la varianza observada de la media disminuirá a medida que $$$\ sigma / \ sqrt {n}$ . La desviación estándar se puede considerar como el error absoluto de la medición promedio, el error relativo en este caso será igual a $$$\ delta = \ sigma / (\ sqrt {n} \ mu)$ . Estas son conclusiones muy generales, independientes de lo suficientemente grandes $$$n$ de la forma de distribución específica de la variable aleatoria investigada. De ellas se desprenden dos reglas útiles (no leyes):

1. Número mínimo de pruebas $$$n$ debe ser dictado por el error relativo deseado $$$\ delta$ . Además, si

$$

$$n \ geq \ left (\ frac {2 \ sigma} {\ mu \ delta} \ right) ^ 2,$$

entonces la probabilidad de que el promedio observado permanezca dentro del error especificado será al menos $$$95 \%$ . En $$$\ mu$ cerca de cero, el error relativo es mejor para reemplazar el absoluto.

2. Sea la hipótesis la hipótesis nula de que la media observada es $$$\ mu$ . Entonces, si el promedio observado no va más allá $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ , entonces la probabilidad de que la hipótesis nula sea verdadera será al menos $$$95 \%$ .


Si se reemplaza en estas reglas $$$2 \ sigma$ en $$$3 \ sigma$ , entonces el grado de confianza aumentará a $$$99.7 \%$ esta es una regla muy fuerte $$$3 \ sigma$ , que en ciencias físicas separa los supuestos del hecho establecido experimentalmente.

Será útil para nosotros considerar la aplicación de estas reglas a la distribución de Bernoulli que describe una variable aleatoria que toma exactamente dos valores, condicionalmente llamados "éxito" y "fracaso", con una probabilidad dada de éxito $$$p$ . En este caso $$$\ mu = p$ y $$$\ sigma = \ sqrt {p (1-p)}$ , por lo que para el número requerido de experimentos y el intervalo de confianza obtenemos

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad y \ quad np \ pm 2 \ sqrt {np (1-p)}.$$

La regla $$$2 \ sigma$ La distribución de Bernoulli se puede usar para determinar el intervalo de confianza al trazar histogramas. Esencialmente, cada barra del histograma representa una variable aleatoria con dos valores: "golpe" - "errado", donde la probabilidad de golpe corresponde a una función de probabilidad simulada. Como demostración, generaremos muchas muestras para tres distribuciones: uniforme, geométrica y normal, después de lo cual comparamos las estimaciones de dispersión de los datos observados con la dispersión observada. Y aquí nuevamente vemos los ecos del teorema del límite central, manifestado en el hecho de que la distribución de datos alrededor de los valores promedio en los histogramas es cercana a la normal. Sin embargo, cerca de cero, la propagación se vuelve asimétrica y se aproxima a otra distribución muy probable: exponencial. Este ejemplo muestra bien lo que quise decir al decir que en estadística estamos tratando con valores aleatorios de parámetros de una variable aleatoria.


Ejemplo que muestra la relación de la estimación de dispersión realizada por la regla $$$2 \ sigma$ y la extensión observada para tres variables aleatorias.

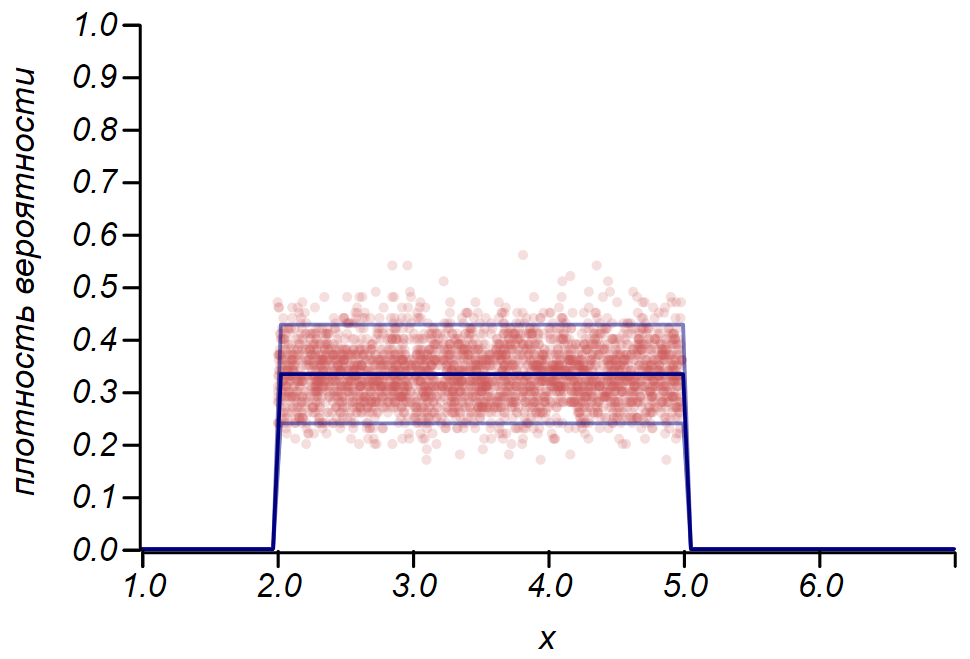
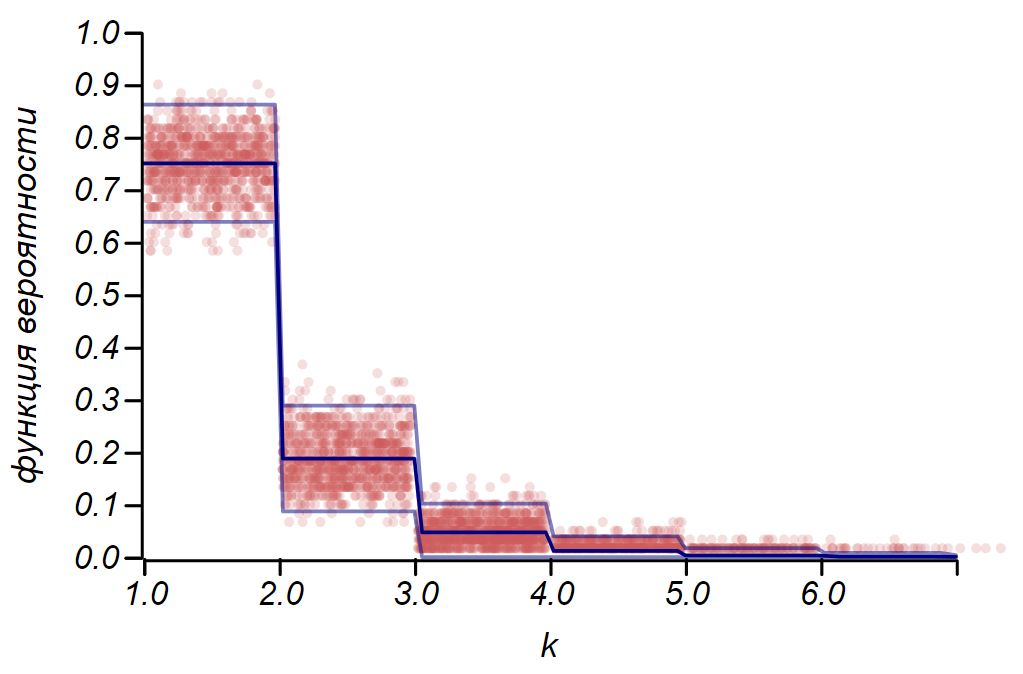
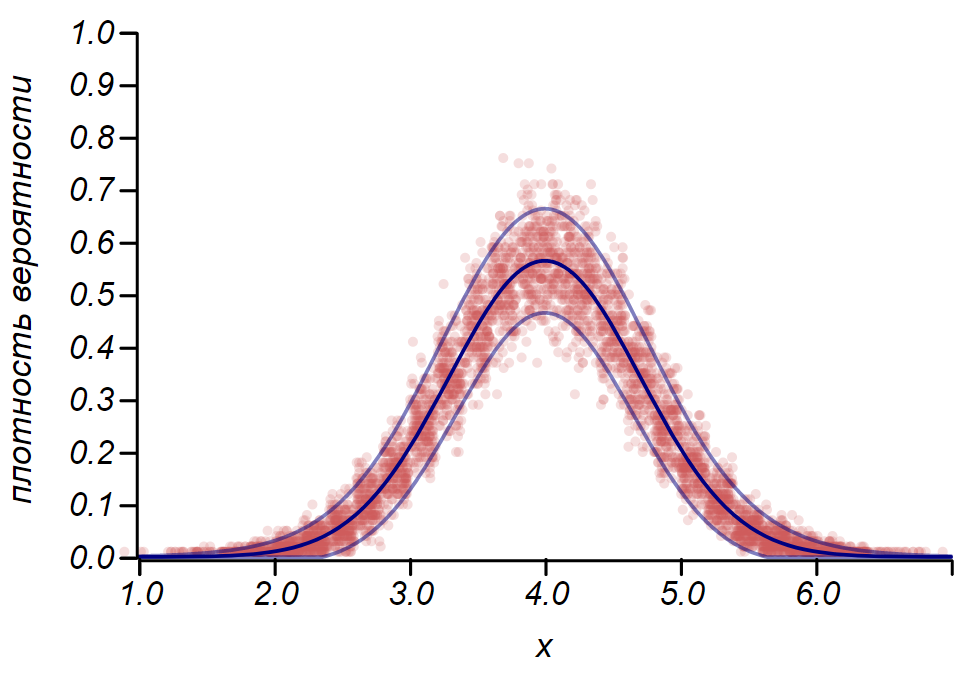
Es importante entender que las reglas $$$2 \ sigma$ e incluso $$$3 \ sigma$ No nos salve de los errores. No garantizan la verdad de ninguna declaración, no son evidencia. Las estadísticas limitan el grado de desconfianza de una hipótesis, y nada más.

El matemático y autor de un excelente curso de teoría de la probabilidad, Gian Carlo Rota, dio un ejemplo en sus conferencias en el MIT. Imagine una revista científica cuyos editores tomaron una decisión decidida: aceptar para publicación exclusivamente artículos con resultados positivos que cumplan con la regla $$$2 \ sigma$ o más estricto Al mismo tiempo, la columna editorial indica que los lectores pueden estar seguros de que con probabilidad $$$95 \%$ ¡El lector no encontrará el resultado incorrecto en las páginas de esta revista! Lamentablemente, esta afirmación puede ser refutada fácilmente por el mismo razonamiento que nos llevó a una injusticia flagrante al evaluar a los conductores por alcohol. Dejar $$$1000$ investigadores experimentados $$$1000$ hipótesis, de las cuales solo una parte es cierta, digamos, $$$10 \%$ . Basado en el significado de la prueba de hipótesis, podemos esperar que $$$900 \ veces0.05 = $ 4$ de hipótesis incorrectas no serán rechazadas por error y se registrarán junto con $$$100 \ veces0.95 = 95$ Resultados verdaderos. Total de $$$130$ ¡Un buen tercero se equivocará!

Este ejemplo demuestra perfectamente nuestra ley nacional de maldad, que aún no se ha incluido en la antología de la merfología, la ley de Chernomyrdin :

Queríamos lo mejor, pero resultó, como siempre.

Es fácil obtener una estimación general del porcentaje de resultados incorrectos que se incluirán en los números de la revista, suponiendo que la proporción de hipótesis verdaderas sea $$$0 <\ alpha <1$ y la probabilidad de aceptar una hipótesis errónea es igual a $$$p$ :

$$

$$x = \ frac {(1- \ alpha) p} {\ alpha (1-p) + (1- \ alpha) p}.$$

Las áreas que limitan la proporción de resultados deliberadamente incorrectos que se pueden publicar en la revista se muestran en la figura.

Estimación del porcentaje de publicaciones que contienen resultados obviamente incorrectos al adoptar varios criterios para probar hipótesis. Se puede ver que aceptar hipótesis por la regla $$$2 \ sigma$ puede ser arriesgado mientras el criterio $$$4 \ sigma$ Ya se puede considerar muy fuerte.

Por supuesto que no sabemos esto. $$$\ alpha$ , y nunca lo sabremos, pero ciertamente es menos que la unidad, lo que significa que, en cualquier caso, la declaración de la columna editorial no puede tomarse en serio. Puedes limitarte a criterios rígidos $$$4 \ sigma$ pero requiere una gran cantidad de pruebas. Por lo tanto, es necesario aumentar la proporción de hipótesis verdaderas en el conjunto de supuestos posibles. Los enfoques estándar del método científico de cognición apuntan a esto: la coherencia lógica de las hipótesis, su coherencia con los hechos y las teorías que han demostrado su aplicabilidad, la dependencia de modelos matemáticos y el pensamiento crítico.

Y nuevamente sobre el clima

Al comienzo del capítulo, hablamos sobre el hecho de que los fines de semana y el mal tiempo coinciden más de lo que quisiéramos. Intentemos completar este estudio. Cada día lluvioso puede considerarse como la observación de una variable aleatoria: el día de la semana que obedece la distribución de Bernoulli con probabilidad $$$1/7$ . Supongamos, como hipótesis nula, la suposición de que todos los días de la semana son iguales en términos de clima y que la lluvia puede llover en cualquiera de ellos con la misma probabilidad. Tenemos dos días libres, por lo que obtenemos la probabilidad esperada de una coincidencia de un mal día y un día libre igual $$$2/7$ , este valor será el parámetro de distribución de Bernoulli. ¿Con qué frecuencia llueve? En diferentes épocas del año, de diferentes maneras, por supuesto, pero en Petropavlovsk-Kamchatsky, en promedio, hay noventa días lluviosos o nevados en un año. Entonces la corriente de días con precipitación tiene una intensidad de aproximadamente $$$90/365 \ aprox1 / 4$ . Calculemos cuántos fines de semana lluviosos deberíamos registrar para asegurarnos de que haya algún patrón. Los resultados se muestran en la tabla.

Periodo de observación	verano	año	$$$5$ años
Número esperado de observaciones	$$$23$	$$$90$	$$$456$
Número esperado de resultados positivos	$$$6$	$$$26$	$$$130$
Desviación significativa	$$$4$	$$$9$	$$$19$
Proporción significativa de lo malo número total de días libres	$$$42 \%$	$$$33 \%$	$$$29 \%$

¿De qué están hablando estos números? Si le parece que durante un año consecutivo no ha habido "verano", esa roca malvada persigue su fin de semana enviándoles lluvia, esto puede verificarse y confirmarse. Sin embargo, durante el verano, la roca malvada puede ser atrapada solo si más de dos quintos de todos los fines de semana resultan ser lluviosos. La hipótesis nula sugiere que solo una cuarta parte del fin de semana debería coincidir con las inclemencias del tiempo. En cinco años de observación, uno ya puede esperar notar desviaciones sutiles que van más allá $$$5 \%$ y, si es necesario, proceda con su explicación.

Aproveché el diario del clima escolar, que se realizó entre 2014 y 2018, y descubrí lo que sucedió durante estos cinco años. $$$459$ días lluviosos de ellos $$$141$ cayó el fin de semana Esto es, de hecho, más que el número esperado por $$$11$ días, pero las desviaciones significativas comienzan con $$$19$ días, así que, como dijimos en la infancia: "no cuenta". Aquí hay una serie de datos y un histograma que muestra la distribución del mal tiempo por día de la semana. Las líneas horizontales en el histograma indican el intervalo en el que se puede observar una desviación aleatoria de la distribución uniforme para la misma cantidad de datos.


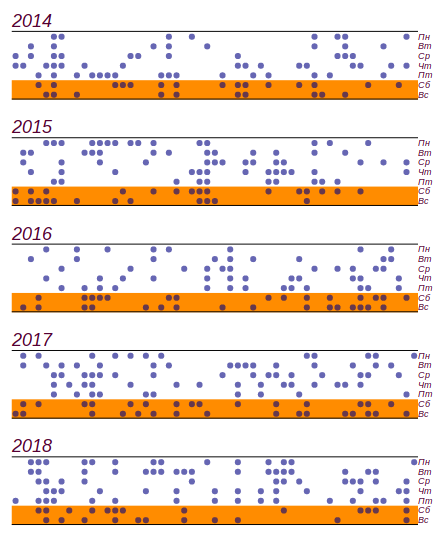
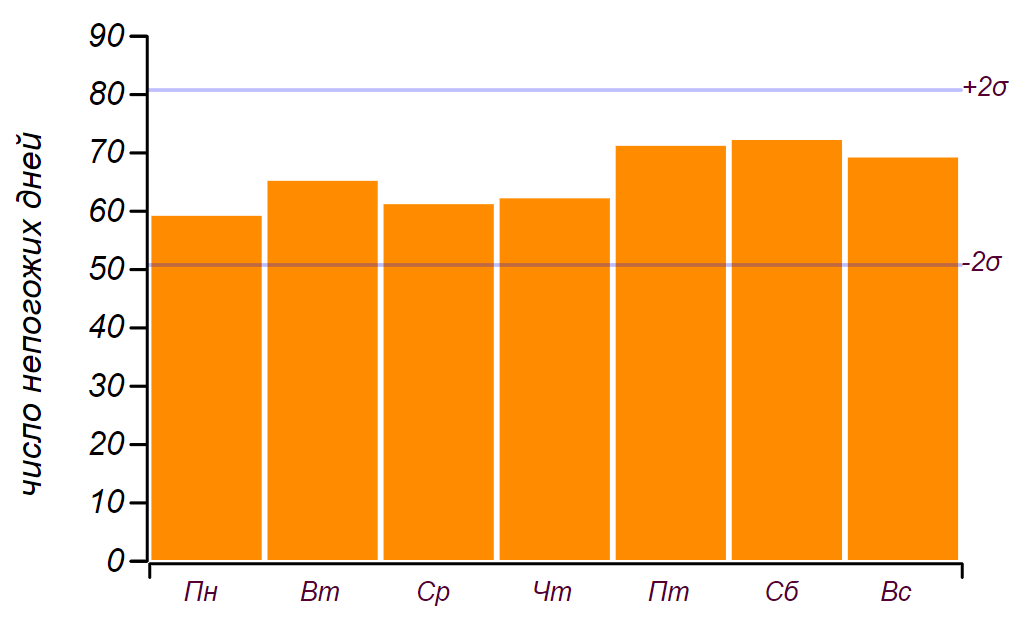La serie inicial de datos y la distribución de días malos por días de la semana obtenidos durante cinco años de observación.

Se puede ver que desde el viernes, de hecho, ha habido un aumento en la cantidad de días con mal tiempo. Pero los requisitos previos no son suficientes para encontrar una razón para este crecimiento: se puede obtener el mismo resultado simplemente clasificando números aleatorios. Conclusión: durante cinco años de observación del clima, acumulé casi dos mil registros, pero no aprendí nada nuevo sobre la distribución del clima por los días de la semana.

Cuando observa las entradas del diario, es evidente que el clima no viene solo, sino en períodos de dos a tres días o incluso ciclones semanales. ¿Esto de alguna manera afecta el resultado? Puede intentar tener en cuenta esta observación y asumir que llueve en promedio durante dos días (de hecho, $$$1.7$ días), entonces la probabilidad de bloquear el fin de semana aumenta a $$$3/7$ . Con tal probabilidad, el número esperado de partidos por cinco años debería ser $$$195 \ pm21$ , es decir, de $$$174$ antes $$$216$ tiempos Valor observado $$$141$ no cae dentro de este rango y, por lo tanto, la hipótesis del efecto de dos días de mal tiempo puede ser rechazada de manera segura. ¿Aprendimos algo nuevo? Sí, aprendimos: parece que una característica obvia del proceso no tiene ningún efecto. Vale la pena considerarlo, y lo haremos un poco más tarde. Pero la conclusión principal es que no hay razones para considerar efectos más sutiles, ya que las observaciones y, lo más importante, su número, siempre hablan a favor de la explicación más simple.

Pero nuestro disgusto no son estadísticas de cinco años o incluso anuales, la memoria humana no es tan larga. ¡Es una pena cuando llueve el fin de semana tres o cuatro veces seguidas! ¿Con qué frecuencia se puede observar esto? Especialmente si recuerdas que el mal tiempo no viene solo. La tarea se puede formular de la siguiente manera: "¿Cuál es la probabilidad de que $$$n$ fin de semana consecutivo será lluvioso? Es razonable suponer que el mal tiempo forma una corriente de Poisson con intensidad $$$1/4$ . Esto significa que, en promedio, una cuarta parte de los días de cualquier período será malo. Observando solo el fin de semana, no deberíamos cambiar la intensidad del flujo, y de todos los fines de semana el mal tiempo debería ser, en promedio, también un cuarto. Entonces, presentamos la hipótesis nula: la tormenta es Poisson, con un parámetro conocido, lo que significa que los intervalos entre los eventos de Poisson se describen mediante una distribución exponencial. Estamos interesados ​​en intervalos discretos: $$$0, \ 1, \ 2, \ 3$ días, etc. por lo tanto, podemos usar el análogo discreto de la distribución exponencial: la distribución geométrica con el parámetro $$$1/4$ . La figura muestra lo que hicimos y se puede ver que no es razonable rechazar la suposición de que estamos observando el proceso de Poisson.


La distribución observada de la longitud de las cadenas de fines de semana fallidos y teóricos. La línea delgada muestra las desviaciones permitidas para el número de observaciones que tenemos.

Puede hacerse esta pregunta: ¿cuántos años necesita hacer observaciones para que la diferencia en $$$11$ días podrían ser confirmados o rechazados con confianza como una desviación aleatoria? Es fácil de calcular: probabilidad observada $$$141/459 = 0.307$ diferente de lo esperado $$$2/7 = $ 0.28$ en $$$0.02$ . Para registrar diferencias en centésimas, un error absoluto de no más de $$$0.005$ eso hace $$$1.75 \%$ del tamaño medido. Desde aquí obtenemos el tamaño de muestra requerido $$$n \ geq (4 \ cdot 5/7) / (0.0175 ^ 2 \ cdot 2/7) \ aproximadamente 32000$ días lluviosos Tomará alrededor de $$$4 \ cdot 32000/365 \ aproximadamente 360 ​​$ años de observaciones meteorológicas continuas, porque solo cada cuatro días llueve o nieva. Por desgracia, este es más que el momento en que Kamchatka es parte de Rusia, por lo que no tengo oportunidad de descubrir cómo son las cosas "realmente". Especialmente si se tiene en cuenta que durante este tiempo el clima logró cambiar drásticamente: desde la Pequeña Edad de Hielo, la naturaleza salió al siguiente nivel óptimo.

Entonces, ¿cómo lograron los investigadores australianos registrar la desviación de temperatura en fracciones de grado y por qué tiene sentido considerar este estudio? El hecho es que utilizaron datos de temperatura por hora que no fueron "reducidos" por ningún proceso aleatorio. Así que más allá $$$30$ años de observaciones meteorológicas lograron acumular más de un cuarto de millón de lecturas, lo que permite reducir la desviación estándar de la media $$$500$ veces con respecto a la desviación de temperatura diaria estándar. Esto es suficiente para hablar de precisión en décimas de grado. Además, los autores utilizaron otro hermoso método que confirma la presencia de un ciclo de tiempo: la mezcla aleatoria de las series de tiempo. Dicha mezcla conserva propiedades estadísticas, como la intensidad del flujo, sin embargo, "borra" los patrones temporales, haciendo que el proceso sea realmente Poisson. La comparación de muchas series sintéticas y experimentales nos permite verificar que las desviaciones observadas del proceso de Poisson son significativas. Del mismo modo, el sismólogo A. A. Gusev demostró que los terremotos en cualquier región forman una especie de flujo autosimilar con las propiedades de agrupamiento. Esto significa que los terremotos tienden a agruparse en el tiempo, formando sellos de flujo muy desagradables. Más tarde resultó que la secuencia de grandes erupciones volcánicas tiene la misma propiedad.

Otra fuente de aleatoriedad.

Por supuesto, el clima, como los terremotos, no puede ser descrito por el proceso de Poisson; estos son procesos dinámicos en los que el estado actual es una función de los anteriores. ¿Por qué nuestras observaciones meteorológicas semanales favorecen un modelo estocástico simple? El hecho es que mostramos el proceso regular de formación de precipitaciones durante un conjunto de siete días o, hablando el lenguaje de las matemáticas, en un sistema de deducciones módulo siete . Este proceso de proyección es capaz de generar caos a partir de series de datos bien ordenadas. A partir de aquí, por ejemplo, hay una aleatoriedad visible en la secuencia de dígitos de la notación decimal de la mayoría de los números reales.

Ya hemos hablado de números racionales, aquellos expresados ​​como fracciones enteras. Tienen una estructura interna, que está determinada por dos números: el numerador y el denominador. Pero al escribir en forma decimal, puede observar saltos desde la regularidad en la representación de números como $$$1/2 = 0.5 \ overline {0}$ o $$$1/3 = 0. \ Overline {3}$ a la repetición periódica de secuencias ya bastante aleatorias en números como $$$1/17 = 0. \ Overline {0588235294117647}$ . Los números irracionales no tienen una notación decimal finita o periódica, y en este caso, el caos reina con mayor frecuencia en una secuencia de números. ¡Pero esto no significa que no haya orden en estos números! Por ejemplo, el primer número irracional encontrado por los matemáticos $$$\ sqrt {2}$ en notación decimal genera un conjunto aleatorio de números. Sin embargo, por otro lado, este número se puede representar como una fracción continua infinita:

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}. $$$

Es fácil demostrar que esta cadena es igual a la raíz de dos resolviendo la ecuación:

$$

$$x-1 = \ frac {1} {2+ (x-1)}. $$$

Las fracciones continuas con coeficientes repetidos se escriben brevemente, como fracciones decimales periódicas, por ejemplo: $$$\ sqrt {2} = [1, \ bar {2}]$ , $$$\ sqrt {3} = [1, \ overline {1,2}]$ . La famosa proporción áurea en este sentido es el número irracional más simple: $$$\ varphi = [1, \ bar {1}]$ . Todos los números racionales se representan en forma de fracciones continuas finitas, algunas irracionales, en forma de infinito, pero periódicas, se llaman algebraicas , lo mismo que no tienen una notación finita incluso en esta forma: trascendental . El más famoso de los trascendentales es el número. $$$\ pi$ , crea caos tanto en decimal como en forma de fracción continua: $$$\ pi \ aprox [3, 7,15,1,292,1,1,1,2,1,3,1,14,2,1, ...]$ . Y aquí está el número de Euler. $$$e$ restante trascendental, en forma de fracción continua, muestra la estructura interna oculta en la notación decimal: $$$e \ aprox [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...]$ .

Probablemente, ningún matemático, comenzando con Pitágoras, sospechó del mundo de la astucia, descubriendo lo que se necesita, un número tan fundamental $$ p i tiene una estructura caótica tan escurridizamente compleja. Por supuesto, puede representarse como sumas de series numéricas bastante elegantes, pero estas series no hablan directamente sobre la naturaleza de este número y no son universales. Creo que los matemáticos del futuro descubrirán una nueva representación de números, tan universal como las fracciones continuas, que revelará el estricto orden oculto por la naturaleza en los números.$\ pi$

$$

$$*\ *\ *$$

, , . , , , . – .

, , , : « – , ». El mundo real es inestable y se esfuerza por esconderse detrás de la complejidad, la aleatoriedad visible y la falta de fiabilidad de las mediciones. La duda en las ciencias naturales es inevitable. Las matemáticas parecen ser un ámbito de certeza, en el que, al parecer, uno puede olvidarse de la duda. Y es muy tentador esconderse detrás de los muros de este reino; considere en lugar de los modelos mundiales irreconocibles que pueden investigarse a fondo; cuenta y calcula, el beneficio de la fórmula está listo para digerir cualquier cosa. Pero, sin embargo, las matemáticas son una ciencia y la duda es una honradez interna profunda que no da descanso hasta que la construcción matemática esté libre de suposiciones adicionales e hipótesis innecesarias. En el ámbito de las matemáticas, hablan un lenguaje complejo pero armonioso, adecuado para razonar sobre el mundo real. Es muy importante familiarizarse un poco con este idioma,para evitar que las cifras se hagan pasar por estadísticas, no permitir que los hechos pretendan ser conocimiento, y que la ignorancia y la manipulación contrasten la ciencia real.